基于有序统计和最大参考单元选择的CFAR算法①

茆星宇， 刘贵如， 王陆林， 李 铮

(1.安徽工程大学计算机与信息学院,安徽 芜湖 241000;2.芜湖易来达雷达科技有限公司,安徽 芜湖 241000)

0 引 言

车载毫米波雷达通过发射线性调频连续波信号，检测目标信息。先将发射信号与接受信号混频，得到差拍信号。然后经过快速傅里叶变换等处理，得到距离-多普勒矩阵。最后通过恒虚警检测器(Constant false alarm rate,CFAR)，检测目标的位置和速度信息。经典的CFAR检测器包括单元平均CFAR (Cell Averaging CFAR,CA-CFAR)[1]，其在均匀环境下有良好的检测性能，但不适用于非均匀环境。之后在此基础上提出了SO-CFAR[2]和GO-CFAR[3]。后续的研究，一是引入一种策略剔除干扰目标[4,5]。二是将CA-CFAR应用于非高斯分布的杂波背景模型[6,7]。三是将CA-CFAR应用于自适应CFAR检测器，这类检测器可以根据背景环境自适应选择合适的处理算法[8,9,10]。除了均值类CFAR检测器外，另一类CFAR检测器包括有序统计CFAR (Ordered Statistics CFAR,OS-CFAR)[11]。OS-CFAR在有干扰目标的环境中保持良好的检测性能，但在杂波边缘环境下虚警率较高。一种改进方式是通过判别分析自动有效的估计合理的k值，从而提高OS-CFAR的性能[12]。为解决OS-CFAR在杂波边缘环境中虚警率偏高的问题，提出一种基于有序统计和最大参考单元选择的CFAR算法。通过将参考窗分为若干个子参考窗，在每个子参考窗内排序并选择第k大的值。然后从筛选出的值中选择最大的值，并乘以门限因子得到检测门限。改进的CFAR检测器既能剔除一定数量的干扰目标，又能抑制杂波边缘环境下的虚警率。

1 CFAR检测器

假设背景功率模型服从高斯分布，经过平方律检波器后，概率密度函数(Probability Density Function，PDF)服从指数分布如式(1)：

(1)

式(1)中，μ为参考单元x的背景噪声功率估计值，可记为式(2)：

μ=μt(1+σI+σC)

(2)

式(2)中，μt为热噪声功率估计值，σI为干扰噪声比(interference-to-noise ratio,INR)，σC为杂波噪声比(clutter-to-noise ratio,CNR)。

1.1 OS-CFAR检测器

图1 OS-CFAR原理图

OS-CFAR原理如图1所示。OS-CFAR检测器先对参考窗中的参考单元排序，然后选择功率第k大的参考单元，并乘以门限因子αOS得到检测门限。为使OS-CFAR保持恒定的虚警率Pfa，OS-CFAR的门限因子可得式(3)：

(3)

式(3)中，Γ(·)表示伽马(Gamma)函数，N为参考窗中的参考单元数，k一般取值为3×N/4。

如果待测单元大于检测门限，则待测单元存在目标H1；反之，则待测单元不存在目标H0。如式(4)所示:

(4)

1.2 改进的CFAR检测器

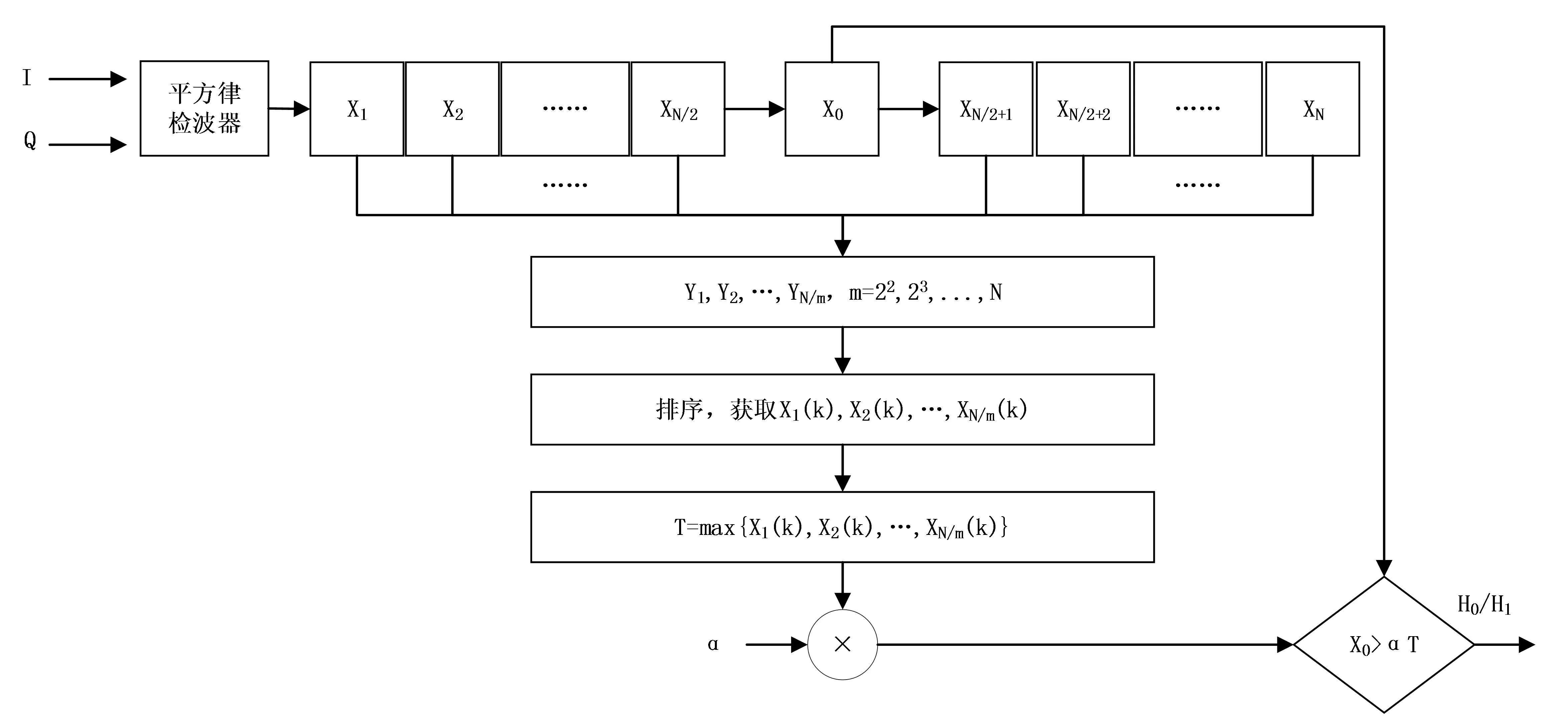
图2 改进的CFAR原理图

改进的CFAR原理如图2所示。改进的CFAR检测器先将参考窗分为N/m个子参考窗Yi,i=1,…,N/m。如式(5)所示：

Yi={X(i-1)·m+1,X(i-1)·m+2,…,Xi·m}

(5)

式(5)中，m为子参考窗中的参考单元数，取值为22,23,…,N。

然后在每个子参考窗Yi,i=1,...,N/m内，对各子参考窗包含的参考单元排序，如式(6)所示:

(6)

最后从每个子参考窗的第k大的值Xi(k),i=1,...,N/m中，选择功率最大的参考单元作为对背景功率水平的估计T，如式(7)所示，乘以门限因子α得到检测门限αT，与待测单元X0比较。门限因子α的值由2.1节所述的方式确定。当待测单元大于检测门限时，待测单元存在目标H1；反之，待测单元不存在目标H0。

T=max{X1(k),X2(k),...,XN/m(k)}

(7)

式(7)中，k取值为3·m/4。

2 仿真实验

2.1 设置参数

设定参考窗中的参考单元数N为32，目标虚警率Pfa为10-4。为使改进的CFAR检测器保持目标虚警率，通过蒙特卡洛仿真得出不同m值时，目标虚警率Pfa对应的α值。如表1所示.

表1 不同m值时Pfa=10-4对应的α值

由于当k取值相同时，m=32的改进CFAR等同于OS-CFAR检测器。仿真实验包括OS-CFAR检测器，但不包括m=32的改进CFAR检测器。由式(3)和表1可得，当N=32且Pfa=10-4时，OS-CFAR的门限因子的值αOS为8.58，m=32的改进CFAR的门限因子α的值为8.50。仿真与公式的误差小于0.1，说明表1中的数据是较合适的。

2.2 均匀环境下的检测性能

均匀环境下各CFAR检测器的检测性能如图3所示。

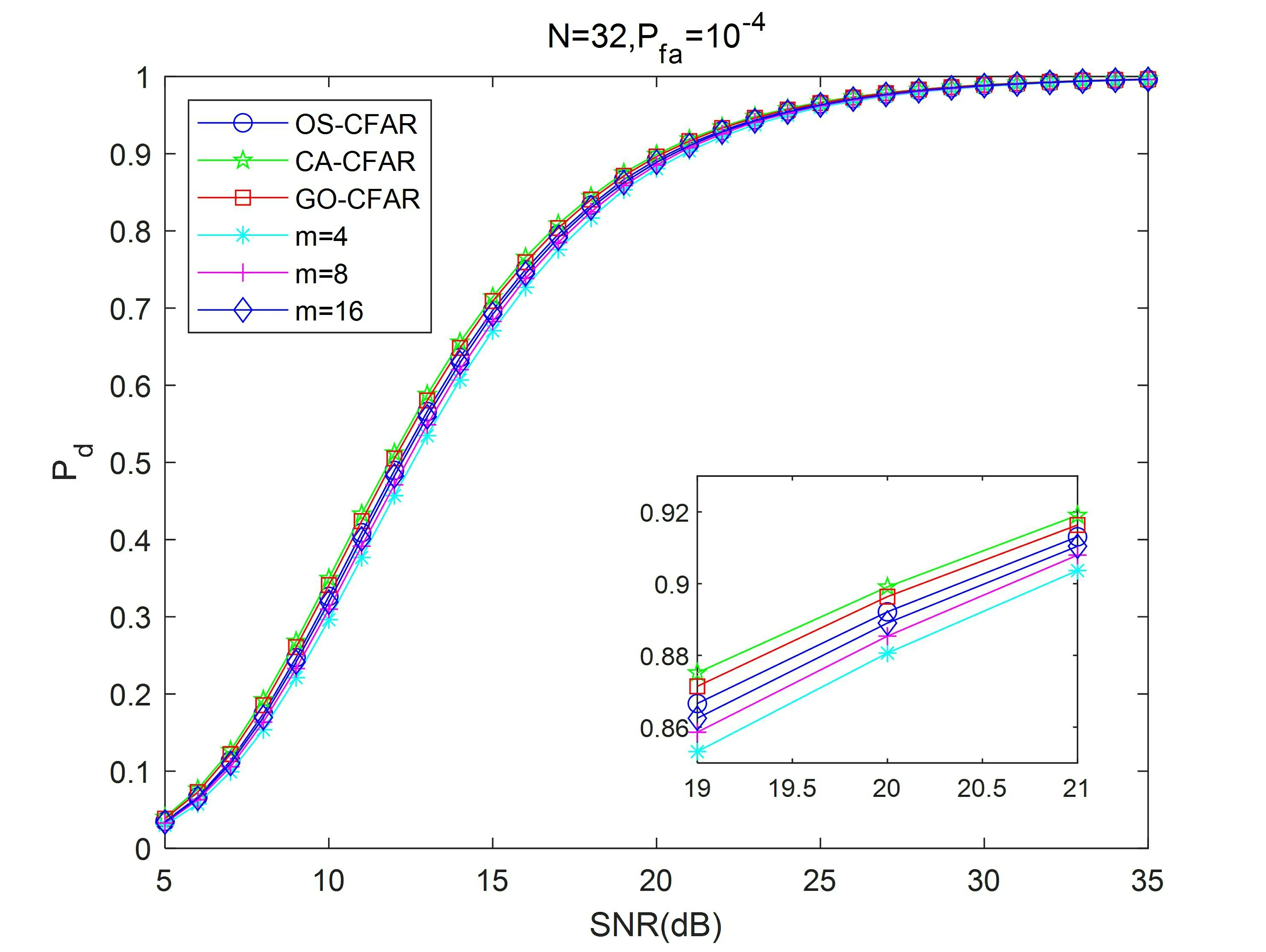
图3 均匀环境下CAFR的检测性能Pd

由图3可得，在均匀环境下，随着m不断增大，改进的OS-CFAR的检测性能不断提高。相比CA-CFAR，其他CFAR检测器在Pd=50%时CFAR损耗从高到低为：GO-CFAR：0.09dB；OS-CFAR：0.29dB；m=16：0.38dB；m=8：0.52dB；m=4：0.71dB。

2.3 干扰目标下的检测性能

假设干扰噪声比INR等于信号噪声比SNR。图4和图5分别显示了左右窗口各一个或两个干扰目标的环境下，各CFAR检测器的检测性能。

由图4可得，在左右窗口各一个干扰目标的环境下，随着m不断增大，改进的CFAR的检测性能不断提高。当m=4，8和16时，改进的CFAR的检测性能略低于OS-CFAR，但优于CA-CFAR和GO-CFAR。当INR=SNR=20dB时，相比OS-CFAR，改进的CFAR的检测性能差异由低到高为：m=16：0.43%；m=8：1.26%；m=4：2.57%。

图5 左右窗口各两个干扰目标下CAFR的检测性能Pd

由图5可得，在左右窗口各两个干扰目标的环境下，随着m不断增大，改进的OS-CFAR的检测性能不断提高。其中，m=4和m=8的改进CFAR检测器性能下降明显，说明了子窗口长度越小，改进CFAR检测器的抗干扰能力就越弱。

2.4 杂波边缘环境下的检测性能

模拟的杂波边缘环境是参考窗从噪声区域(含杂波参考单元数为0时)移动到杂波区域(含杂波参考单元数为N时)。当含杂波参考单元数为N/2+1时，待测单元正好位于杂波区域，此时CFAR检测器的虚警率最高，即虚警峰值。图6显示了CNR=5dB时，改进的CFAR与OS-CFAR，CA-CFAR，GO-CFAR的虚警率。

图6 杂波边缘环境下CFAR的实际虚警率Pfa

由图6可得，当待测单元位于噪声区域时(含杂波参考单元数小于N/2)，改进的CFAR的虚警率低于OS-CFAR，高于CA-CFAR和GO-CFAR。当待测单元位于杂波区域时(含杂波参考单元数大于N/2)，改进的CFAR的虚警率低于OS-CFAR和CA-CFAR，略高于GO-CFAR。另外，相比m=16，大多数情况下m=4和m=8的改进CFAR检测器的虚警率更低。

2.5 复杂环境下的检测门限

图7模拟了在距离维上改进CFAR和OS-CFAR检测器的检测门限。在模拟的场景中，在1-200的距离单元内存在3个真实目标，其位置分别在51，55和100，且信噪比为30～35dB。另外，在30和150的距离单元处分别存在CNR=-30dB和CNR=30dB的杂波边缘过渡。图7(a)，(b)和(c)分别给出了13-188的距离单元内，m=4，m=8和m=16的改进CFAR与OS-CFAR检测器在目标虚警率Pfa=10-4时的检测门限。

由图7可得，改进的CFAR和OS-CFAR都检测到了三个真实目标。但是，m=16的改进CFAR和OS-CFAR在150的距离单元处存在虚警。由图7中的检测门限可得，改进的CFAR比OS-CFAR检测器更能抑制杂波边缘处的虚警，并且m值越小，改进的CFAR对杂波边缘处虚警的抑制效果越好。这与2.4中的结论是一致的。

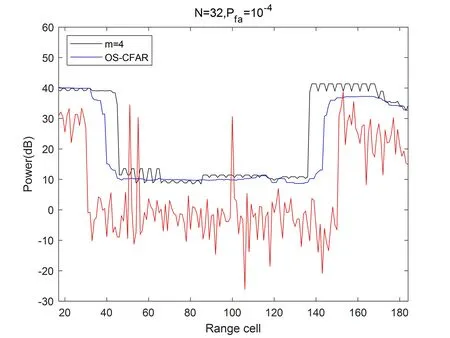
(a)

综合各种环境下的仿真实验，子参考窗的理想长度应为8或16，此时，改进的CFAR在均匀环境、多目标环境和杂波边缘环境下的综合效果最优。

3 结 语

提出一种基于有序统计和最大参考单元选择的CFAR算法，通过将参考窗分成若干个子参考窗，然后在每个子参考窗内采用OS-CFAR的策略选取一个合适的值，最后从这些值中选取最大值用于生成检测门限。仿真实验表明，相比OS-CFAR检测器，改进的CFAR牺牲了一些在均匀环境和多目标环境下的检测性能，有效的降低了杂波边缘环境下的虚警率。