基于BP人工神经网络预测地热井中流体的结垢位置

李帅，刘明言，2，马永丽

（1 天津大学化工学院，天津 300350；2 化学工程联合国家重点实验室（天津大学），天津 300350）

我国具有丰富的地热资源和能源，开发利用潜力大[1-3]。但是，在地热开发利用过程中，遇到的主要技术难题是地热流体在井筒或地面系统中的结垢和腐蚀问题[4-6]，从而制约着地热资源和能源的高效可持续开采和利用。地热井筒中的流体结垢可以显著减小井筒的流通截面，降低地热能的采出率和利用率[7-8]，因清洗而增加额外运行维护成本等[9-10]，还有可能形成生产安全问题[11-13]。故需要准确预测地热流体在井筒中的结垢位置，为下沉潜水泵及阻垢剂加注等提供指导。地热流体的结垢是一个非常复杂的动态过程[14-15]，预测结垢位置主要应通过机理建模等方法实现[16-18]。然而，现有的机理模型还难以预测地热流体结垢过程的全部特征，预测精度也不够理想。因此，如何建立准确、可靠的地热流体结垢模型是目前亟待解决的问题之一。国内外研究者基于化学热力学和相关实验研究[19-20]，开发了许多软件和相关程序模拟地热流体在井筒中的结垢过程[21-29]。Pátzay 等[24]使用Davies 和Pitzer 活度系数计算方法开发了用于CaCO3-H2O-CO2系统中方解石结垢形成的平衡模拟算法和计算机程序，用于确定地热井口中不同气体（如CO2、CH4和N2）浓度下的地热流体在井筒中的闪蒸点位置和气体分压的分布情况。Akin 等[25-26]利用PHREEQC 软件，计算出土耳其Kizildere地热田的碳酸钙在闪蒸点之上80m 处左右产生结垢。HOLA[27]和WELLSIM[28]等软件程序也可以计算地热井筒中闪蒸点的位置，两种软件的区别只是在于前者没有考虑地热流体中盐分和不凝气体含量对闪蒸点位置的影响，而后者则需要同时考虑这两个参数的影响。Garg等[29]则利用新建立的相含率经验关联式，模拟分析地热井筒中温度和压力随着井筒深度的变化规律，以判断闪蒸点的位置。

人工神经网络（artificial neural networks，ANNs）是一种仿照生物大脑神经元运行的学习算法，因为其具有较好的非线性拟合效果和对不相关变量的抗干扰能力，而且其只需要依据含有输入和输出变量的训练数据集进行相关模型训练以便建立准确的预测模型，通过选择最优的训练算法和不同激活函数，就可以较好地达到所预期的精度要求，无须对具体过程进行特别复杂的数学推导[30]。故在许多研究领域，ANNs 是一种有效的计算工具，用于建模和预测，以解决复杂的实际问题[31]。在地热领域中也有利用人工神经网络对各种变量进行预测的报导[32-34]。地热流体在井筒中的结垢是一个复杂的化学热力学和化学动力学过程，受到多种因素的共同影响，如地热流体的温度、压力以及流量等，具有非线性度高和耦合性强等一系列特征。因此，可以尝试将ANNs可拟合非线性函数的功能应用到地热流体在井筒中的结垢位置预测中。鉴于此，本文提出基于BP 人工神经网络对地热流体在井筒中的结垢位置进行预测，主要研究BP 人工神经网络的结构、预测结果和特点等，为之后在井筒内地热流体结垢位置以下注入阻垢剂和物理增压潜水泵的下入深度等提供依据。所采用的ANNs 模型适用于Windows的MATLAB软件进行仿真，该软件是推荐用于可视化和高性能数值分析的计算机程序。

1 地热井结构及测试数据

1.1 地热井的选取

本文研究的两口地热井位于河北省博野县，井深结构皆为四开。其中第一口地热井的结构如图1所示，具体的结构及数据如表1所示。本地热井的取水层为雾迷山组白云岩含水层，在2019 年11 月完井，最终的成井深度为3860m，3275.00～3860.00m 为所利用地热井的井段深度，该地热井的含水层总共为11 层，总厚度为38.10m，其中有总厚度为9.1m 的两层二类裂隙缝层，总厚度为29.0m的九层三类裂隙缝层。现场放喷实验出现了明显的结垢问题。在距离地面1.5m 处开始在井筒的泵管中结垢，即结垢位置为1.5m。通过SEM 和XRD 的分析结果可知，垢样中的碳酸钙质量分数大于96%[35]。

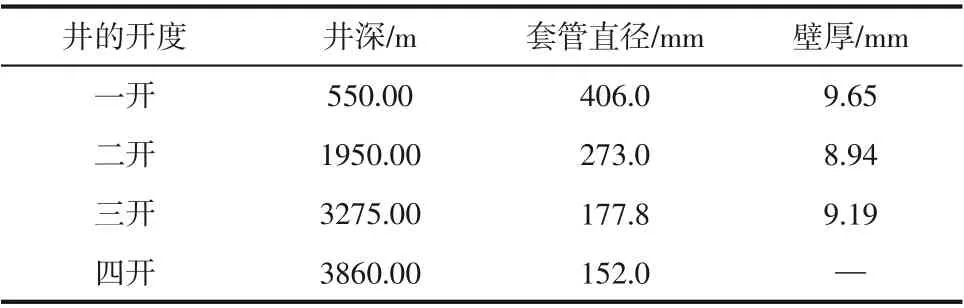
表1 地热井四开的井深结构数据

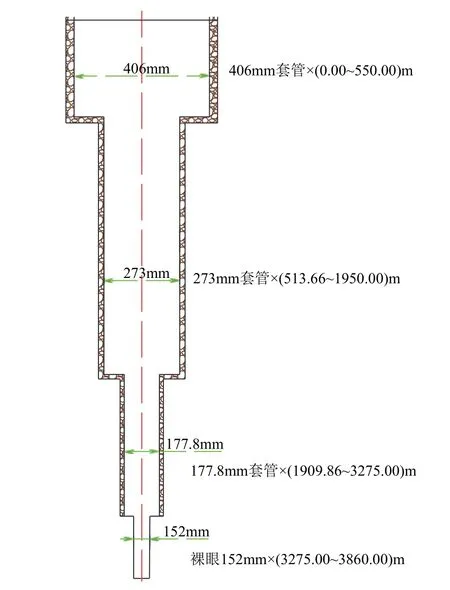
图1 博野县某地热井的井深结构

地热流体的井口温度和压力、井底温度和压力等参数是利用测井仪器设备对现场地热井进行探测获得的。测试从井底到井口的温度和压力，每隔10m记录一套数据。对该井的井口流体温度进行采样分析可知，在井口温压测点测得的温度为95℃，压力为0.186MPa。液态地热流体的流量为100m3/h，井底温度为116℃，压力为28MPa。

1.2 地热井结垢分析

地热流体经过亿万年的地质运动，已经变为CO2的过饱和溶液，故地热流体中存在着大量的HCO-3。当地热流体沿地热井筒上升时，随着地热流体在井筒内压力的不断降低，当其液相中地热水的分压低于上升时温度所对应的饱和蒸汽压时，会出现闪蒸现象。当闪蒸发生以后，地热流体会从原来的单相流动变为气液两相流动，而此时气相中的水蒸气含量会迅速增加，稀释气相中的CO2。同时还有其他气体（如CH4、N2和H2S 气体）侵入和地热井筒的腐蚀，也会导致原来气相中的CO2气体减少。这样，气相中的CO2分压会迅速降低。同时，地热流体中溶解的CO2气体就会大量释放到气相中，使反应式(1)向右进行，使得地热流体中的pH增大，将地热流体中存在过饱和的HCO3-解离出的H+中和[反应式(2)向右进行]，最终导致地热流体中产生大量的CO32－，和地热流体中原来就存在的大量Ca2+进行结合，导致碳酸钙沉淀析出，发生结垢现象[反应式(3)向右进行]，从而附着在地热井的井筒内壁上。地热流体在井筒中的实际结垢位置由现场测得。

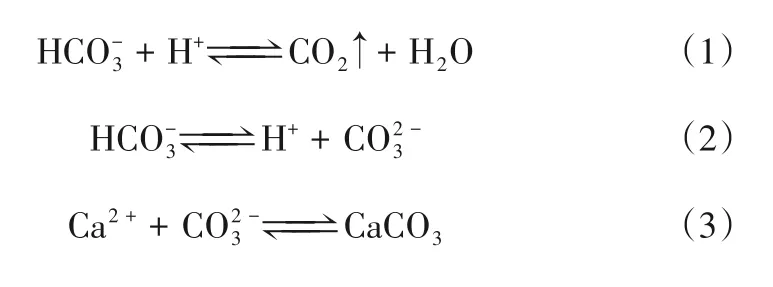
2 BP人工神经网络

2.1 预测方法简介

ANNs 是将人脑结构组织和运行机制进行了某种抽象、简化和模拟[36]。BP（back propagation）人工神经网络是一种多层前馈神经网络，并且可以按照误差逆向传播算法进行训练，是目前应用最广泛的神经网络之一[37-38]。基于BP人工神经网络对地热流体在井筒中的结垢位置预测的结构分为3 层：8 个输入层、13 个隐含层和1 个输出层，称为8-13-1 网络结构，具体结构见图2。8 个输入层的变量具体为井底温度和压力、井口温度和压力以及井筒深度（井筒为四开井，4个变量）。

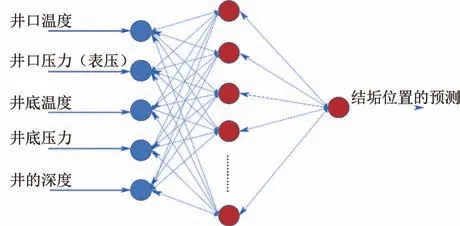
图2 BP人工神经网络的结构

在已知博野地热井的实际结垢位置为距离地面的1.5m处后，利用BP人工神经网络进行训练集的训练。之后，由于该地热井的一些参数发生改变，进而地热流体在该井筒中的结垢位置会发生改变。利用BP 人工神经网络，基于地热井的变化参数，可预测出地热流体在这口井内新的结垢位置。

2.2 BP人工神经网络预测地热流体在井筒中的结垢位置所采用的算法

在利用BP 人工神经网络预测地热流体结垢位置时，使用的误差函数是Mu参数。在基本的神经网络权重基础上Mu参数可再加一个调节调制，这样就可以在训练的过程中避免陷入局部最小值，从而导致找到的最优值发生严重的错误。Mu 参数的范围为0～1。预测地热流体在井筒中的结垢位置时，选择的训练函数是Levenberg-Marquardt 算法（即L-M 算法），这也是最优化算法中的一种。LM算法是介于牛顿法与梯度下降法之间的一种非线性优化方法。神经网络的性能主要通过均方差来进行评价。L-M 算法是将被估计量和估计量之间进行差异化度量。

2.3 预测地热流体的结垢位置的BP人工神经网络的数学模型

预测地热流体在井筒中的结垢位置时，其BP人工神经网络中神经元的激活函数是输入信号xi和权重因子wji的加权和，如式(4)。

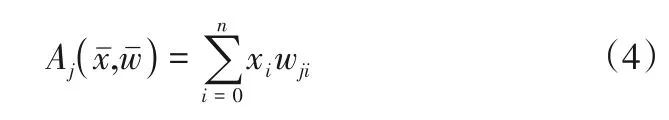
由式(4)可知，Aj仅与xi和wji相关，输出函数（即Oj）假设不发生变化，则可以认为该神经元函数是线性函数。但是这样的神经元函数其局限性比较大。输出函数在神经网络中经常使用的是S型函数，如式(5)。

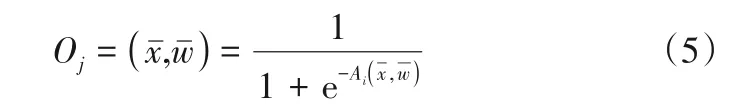
Oj只与Ai有关，而Aj又与xi和与其相对应的wji有关。误差值（即Ej）是真实值（即Oj）与预期值（即dj）的差，并且wji强烈地影响着dj，所以可以通过改变wji来使dj最小化。对每个神经元函数的误差值进行定义，如式(6)。

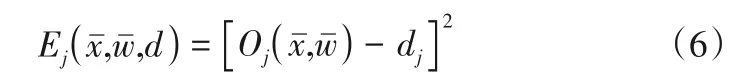
Ej越大，则可以知道Oj与dj之间产生的差值越大。在输出层上神经元函数的所有误差进行求和就可以得到神经网络整体的Ej， 如式(7)。

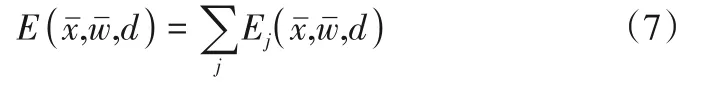
所调整的相关权值则是利用梯度下降法来进行的，如式(8)。

wji与Ej的改变将会调整每个神经元的Δwji，而对神经元函数的调整是E关于wji的导数。每次对神经元误差的调整步长为η。而对Ej影响大的wji相比于影响小的wji，所进行调整的值也相应地变大。

循环计算公式(4)～(8)直到遇见合适的wji停止进行运算。BP 人工神经网络算法的主要目的是对E关于wji的导数进行求解。首先对E关于Oj的函数进行求导运算，如式(9)。

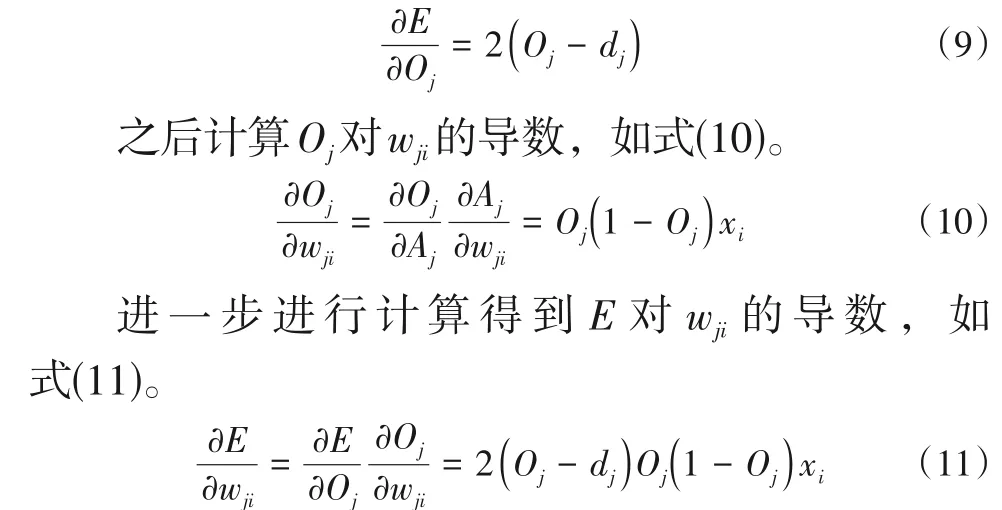
故，将每个wji调整，如式(12)。

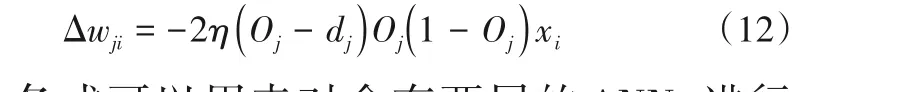
以上各式可以用来对含有两层的ANNs 进行训练。

2.4 BP人工神经网络预测地热流体在井筒中的结垢位置时常用的激活函数

（1）线性函数，如式(13)。

在利用BP 人工神经网络预测地热流体在井筒中的结垢位置时，所使用的激活函数主要是线性函数和Tanh函数。

2.5 BP人工神经网络预测地热流体在井筒中的结垢位置的归一化

当预测地热流体在井筒中的结垢位置时，其使用的BP 人工神经网络需要进行归一化处理，这样可以将输入信号通过神经网络得到输出结果的最优值。BP 人工神经网络的归一化主要是将输入信号映射到[0，1]或[-1，1]区间或其他的区间。但是因为所使用输入信号的单位不同，输入信号的区间有些会比较大，最后会有训练时间长和收敛慢的结果产生。在模式分类中区间大的输入信号产生的作用可能会偏大。因此对BP 人工神经网络的归一化处理也主要是为了防止数据湮灭等现象的产生。输出层激活函数的值域是需要进行制约的，主要是为了将训练的目标信号可以在激活函数的值域中得到很好的映射。

在用MATLAB 来实现BP 人工神经网络预测地热流体在井筒中的结垢位置时，归一化处理数据可以采用postmnmx、tramnmx这两个函数。

2.6 BP 人工神经网络训练集、测试集的作用和训练方法及函数

BP 人工神经网络是一种有导师的机器学习，其所需要的数据集通常被分为2～3 个，即训练集、验证集和测试集。其中，在BP 人工神经网络预测地热流体在井筒中的结垢位置时，所给出的训练集与测试集都是围绕着河北省博野县某地热井中相关数据，在一定范围内随机取出的样本；训练集是用来提高神经网络预测结垢位置的准确性；而测试集主要是用来检验最终选择的最优模型的性能如何，即检验神经网络预测结垢位置的准确性，检测其准确性是否达标。在这个过程中没有用到验证集。表2 为使用MATLAB 实现BP 人工神经网络预测地热流体在井筒中的结垢位置里输入训练集时，所需要考虑的训练方法及其对应的函数。对地热流体在井筒中的结垢位置预测时，所采用的训练及算法为Levenberg-Marquardt（L-M），L-M 算法是在高斯-牛顿法的基础上加入了一个变量因子，进而预测得到进一步改善。

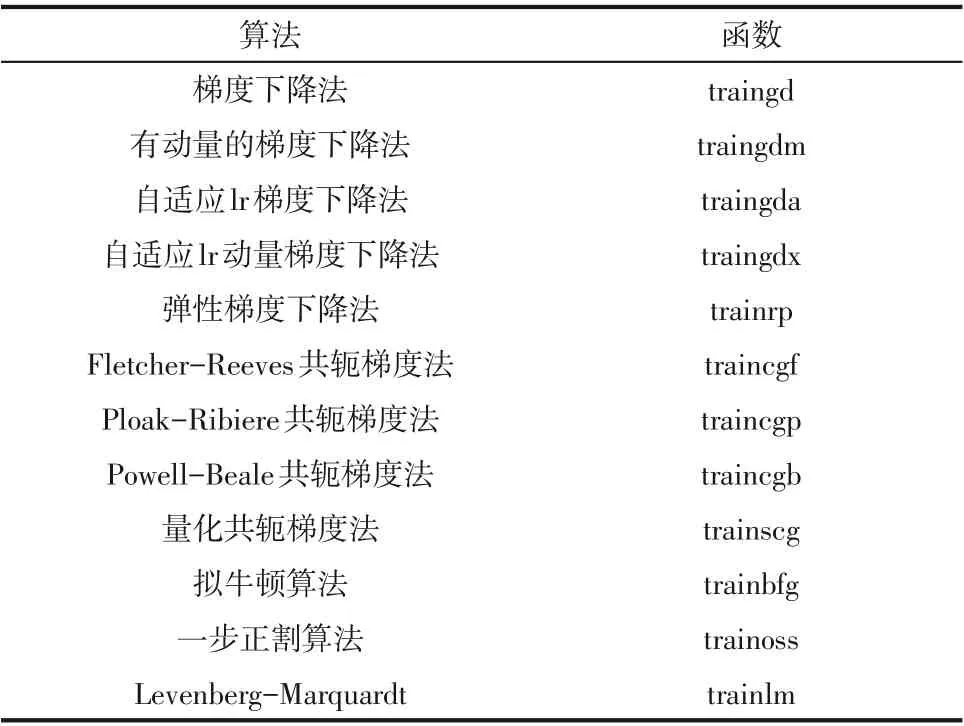
表2 训练方法及其函数

2.7 影响结垢位置的关键影响因素与参数设置对预测结果的影响

影响结垢位置的关键影响因素主要有井口的温度和压力、井底温度和压力以及井筒的结构深度。但是还有一些其他相较而言影响不是很明显甚至可以忽略的因素，例如，井口中所测得的不凝气体的含量等非常复杂的因素，还会涉及钙离子和碳酸根离子的活度，甚至地热流体的酸碱度也会影响其在井筒中的结垢位置。

在BP 人工神经网络中隐含层节点个数对其识别率影响不是很大。但是，如果节点个数过多，则会相应增加神经网络的运算量，这样产生的直接后果就是训练时间特别长。然而激活函数无论对于识别率还是训练时间都有着明显的差异。在拟合高次函数时，函数所需要的精度越高，其进行的计算量也会相应越大。学习率会影响训练时间和BP 人工神经网络能否最终收敛。如果将学习率设置比较小，则可以保证神经网络最后收敛，但是收敛速度将会特别慢。

利用MATLAB 实现BP 人工神经网络预测地热流体在井筒中的结垢位置的计算机程序如图3 所示。采用的学习率为0.0001，系统误差小于0.01。BP 神经网络在经过300000 多次迭代后收敛。此时，训练学习阶段结束。训练结束后的BP 神经网络就可以用来预测地热流体在井筒中的结垢位置。

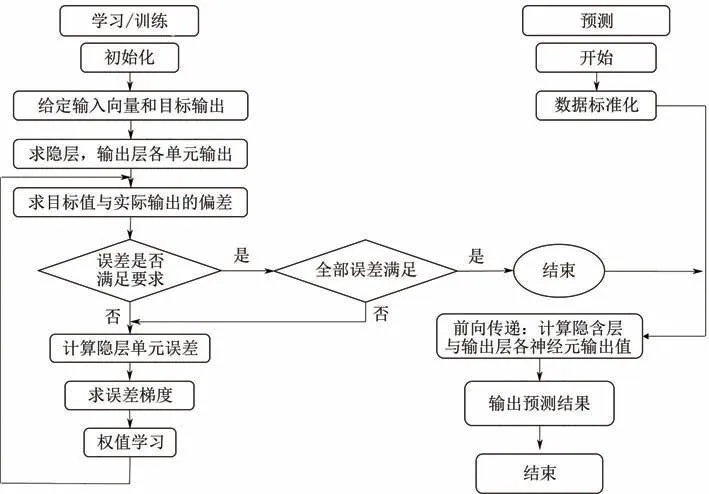
图3 BP人工神经网络预测地热流体在井筒中结垢位置的程序框图

3 结果与讨论

3.1 BP人工神经网络训练的性能分析图

3.1.1 训练集和测试集中的预测值与实际值的分析

图4为训练集中的结果对比，其中(a)为训练集中实际值与预测值的对比，其均方差为0.0043；(b)为神经网络中预测值与实际值之间的拟合效果；(c)为最终得到的结垢位置的相对误差。可以看到图4中预测值与实际值的拟合效果非常吻合，说明利用BP 人工神经网络所预测的地热流体在井筒中的结垢位置和实际结果达到了很好的匹配。根据图4 可知，随机抽取的800 个样本已经很好地预测了地热流体在井筒中的结垢位置。

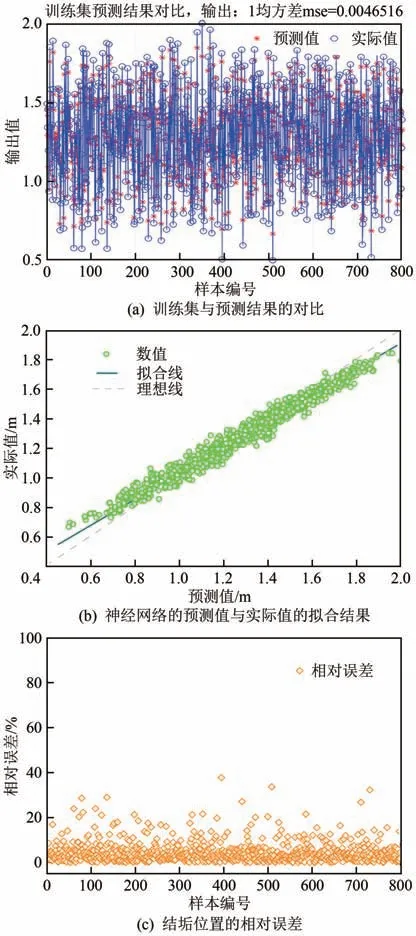
图4 训练集中的结果对比

图5为测试集中的结果对比，其中(a)为训练集中实际值与预测值的对比，其均方差为0.0047；(b)为神经网络中预测值与实际值之间的拟合效果；(c)为最终得到的结垢位置的相对误差。通过对训练集中的800 个样本的训练，BP 人工神经网络可以很好地对不在训练集中的样本进行较为准确地拟合。图5的拟合效果非常好。所以，当地热流体在井筒中结垢时，其在井筒底部的温度和压力以及井深和井口温度发生变化时，地热流体的结垢位置会随着这些参数的变化而发生变化，进而达到对地热流体结垢位置的准确预测。

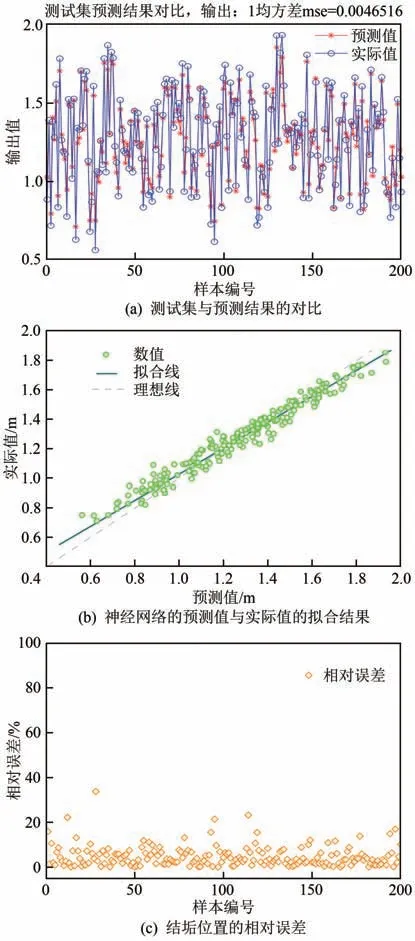
图5 测试集中的结果对比

3.1.2 训练集、测试集和总体的均方差随训练次数的变化

训练集、测试集和总体的均方差随训练次数的变化如图6所示。由图6可知，训练集和测试集在训练开始时其均方差比较大。之后，随着训练次数的增加，其均方差逐渐减小，最终到达目标值。图6 中的小圆圈位置代表终止的训练次数（即代数）处的均方差。当训练次数为2次时其均方差就达到了目标值。

图6 训练集、测试集和总体的均方差随训练次数的变化

3.1.3 BP神经网络各阶段的训练

图7 为BP 人工神经网络在各个阶段时的训练结果。

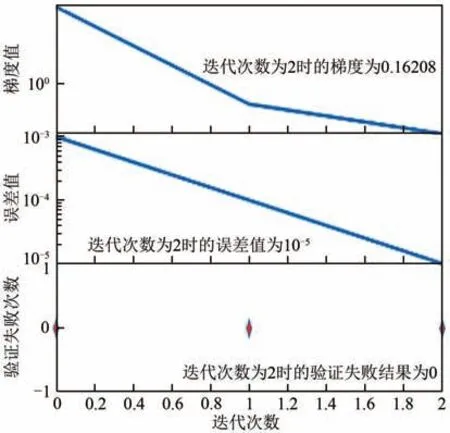
图7 BP神经网络各阶段的训练

可以看出，随着训练次数的增加，L-M 算法的梯度从开始下降的速度越来越快，到之后下降速度逐渐变缓；而误差精度曲线则呈阶梯式下降，表明该算法的误差精度越来越精确。

3.1.4 各个样本集合总体的相关性分析

图8 为各个样本集合总体的相关性分析结果。从图8 可知R=0.986，说明在地热水结垢位置的预测中，其各个样本集合总体相关性的拟合性很好，说明所取的样本数据相关性很好。即通过地热水在井底和井口的参数以及其井深参数与最终的结垢位置有很好的相关性。

图8 各个样本集合总体的相关性分析图

3.1.5 地热井内地热流体结垢位置的预测

根据BP 人工神经网络算法，输入层有8 个变量，分别是井底温度和压力、井口温度和压力以及井筒深度（井筒结构为四开，相当于四个变量）。如表3第一行所示为根据河北省博野县第一口地热井得到的实际数据，而第二行则为博野县第二口地热井所得到的实际数据（作为对比数据），目的是为了验证当初始条件（地热流体在井口和井底的温度压力以及井深的相关数据）发生变化后，地热流体在井筒中的结垢位置与实际的结垢位置是否相差很大，进而测试BP 人工神经网络预测地热流体在井筒中的结垢位置的相对误差。输出层则为预测地热流体在井筒中的结垢位置，如表4所示。表3里的内容是利用MATLAB 所形成的BP 人工神经网络预测地热流体在井筒中的结垢位置的输入数据，而表4则是根据BP人工神经网络在将表3的数据输入之后得到的最终结果。因此，表3是表4所对应的条件。将输入变量归一化在封闭的计算域中[-1,1]（也就是基于输入变量分布的标准偏差和等于零的平均值）中工作。为了确定BP 人工神经网络的最佳结构，所采用的灵敏度分析是通过调整所需的样本数、训练次数和激活函数的类型来执行的。测试中不包括传统的线性激活函数，因为地热流体的结垢位置预测是高度非线性的。

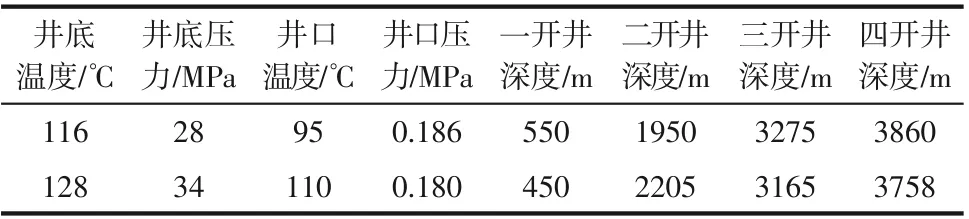
表3 数据库输入数据

河北博野现场下泵的深度近200m，泵管的直径为159mm。当地热井运行半个月后，泵管在井下1.5m左右可以看到厚度约10mm的垢层。由于碳酸钙结垢有一个诱导期和生长过程，由此可推测井壁上的结垢发生可能更早，开始结垢的位置更深。若取结垢位置为1.5m时（即利用BP人工神经网络来预测地热流体的结垢位置时需提前输入其大致的结垢位置来进行目标训练），通过BP人工神经网络计算出的预测结垢位置为表4所示，其相对误差在10%以内。所以，利用BP 人工神经网络预测地热水在井筒中的结垢位置是可行的。

表4 预测结果值与实际值的对比

因为连续监测地热井的井底数据是不切实际的，而且地热开发人员通常对井口的流动压力、温度和流量更感兴趣。而随着地热流体的回注，地热储层以及井底和井口的温度和压力也会产生明显的下降行为，所以此时地热流体在井筒中的结垢位置也会发生相应的变化，这时可利用BP 人工神经网络预测地热流体在井筒中的新的结垢位置，这样可节省因使用设备重新检测地热流体在井中结垢位置的成本、时间和精力。但是，地热井筒内的两相流具体结垢位置的判断较为复杂，取决于流型、生产数据和井筒几何形状以及流体特性等多个变量。因此，BP 人工神经网络并不能取代正常的数值建模预测，而是旨在快速获得新的结垢位置，这在很大程度上有助于日常的决策过程，而且不至于使地热井停止运行，产生不必要的成本。利用BP 人工神经网络预测地热井筒中的结垢位置，为地热开采中的结垢预测提供了一种新的思路和方法。

需要说明的是，BP 人工神经网络更适合于对同一口地热井中，因为井底温度和压力及井口温度和压力发生变化而产生的新的结垢位置的预测，也就是对于同一口地热井中因操作条件等改变后的再次结垢位置的预测。但是，由于缺少改变井口操作条件后的现场结垢位置数据，因此，没有进行这方面的预测对比研究，可作为今后进一步研究的一个方向。

4 结论

（1）开发了一种ANNs 代理模型，该模型由8个输入层、13个隐藏层和1个输出层组成，用于根据井口和井底数据以及事先测得的井筒中的实际结垢位置预测当条件发生变化后，地热流体新的结垢位置。输入层由一系列可选择的变量组成（井口温度、压力，井底温度、压力和四开井中每开井的深度），而输出层只有一个，就是预测的结垢位置。使用800个训练样本进行训练，使该模型的预测更加准确。利用位于河北省博野县的地热井数据展示了该代理模型的用途和优势，得到了较好的结果。

（2）BP 人工神经网络预测方法不能代替地热井筒结垢位置的具体模拟程序预测方法，而是旨在获得已知地热井结垢位置的基础上的快速结垢位置计算。有助于日常的决策过程，可以节省昂贵的勘测以及试井费用。但是，在准确性方面，该模型不能替代实际的操作程序，而是在无法试井或由于各种原因无法测量时，作为预测模型的补充。

（3）利用BP 人工神经网络预测地热流体在井筒中的结垢位置与实际值的误差在10%以下。可以看到，两口井的预测结果误差都很小，可以认为对于同一口井，改变操作条件，其预测结果是准确的。应用人工神经网络分析地热井筒的结垢情况后表明：BP 人工神经网络无须建立复杂的流体流动和传热以及化学反应数学模型。其学习过程主要是通过自动调节神经元之间的连接权值完成，在选取有代表性的训练样本情况下，人工神经网络能够成功地预测和评判地热井筒的结垢情况。

（4）人工神经网络的优点是：误差小，实测数据与预测结果很接近，在预测碳酸钙结垢时取得了较好的效果。其不足是：样本数据依赖于以往所进行的监控地热井筒的温度和压力数据，样本数据采集困难，所以应用不广泛。但是，人工神经网络具有强大的自组织和自学习的能力，利用它预测评判地热流体的结垢情况，能够因此而解决由于寻找各种复杂因素对结垢影响规律的难题。

符号说明

Aj——神经元激活函数

dj——神经元的期望函数

Ej——神经元的误差函数

Oj——神经元的输出函数

wji——神经元的权重系数

xi——神经元的输入变量

η——神经元中梯度下降法的步长

下角标

i——第i个神经元

j——第j个神经元