参数化混合口令猜测方法

韩伟力 张俊杰 徐 铭 王传旺 张浩东 何震瀛 陈 虎

1(复旦大学数据分析与安全实验室 上海 200438)2(华南理工大学软件学院 广州 510006)(wlhan@fudan.edu.cn)

迄今为止，基于文本口令的身份认证仍是保护用户个人信息和在线财产的最流行方式之一[1].尽管近年来研究人员提出了各种身份认证方法，例如基于指纹或手势的身份认证[2]，但因口令易用和低成本的显著优势[3-4]，互联网用户仍倾向于使用文本口令.

为更好地研究口令的安全性，研究人员提出了多种数据驱动的口令猜测方法，如概率上下文无关文法(probabilistic context-free grammars, PCFG)[5]、马尔可夫(Markov)方法[6]和长短期记忆(long short-term memory, LSTM)[7]神经网络方法，并致力于优化这些猜测方法[8-17].由于这些方法具备不同的猜测优势，即能够以更小的猜测数猜中特定类型的口令，Ur等人[18]提出使用每条口令被不同方法猜中所需要的最小猜测数作为评估该口令安全性的保守指标，称为“Min_auto”.这样的保守指标完美地结合了不同方法的猜测优势，可以看作是多方法混合猜测的理想上界.但在实际的猜测场景中，实现Min_auto的猜测效果需要的猜测数是单一方法的多倍，且不同方法会生成大量重复的猜测口令，严重浪费了计算资源.

为了在实际猜测的场景中减少计算资源的浪费，并在有限的猜测数内最大化地利用不同方法的猜测优势，本文提出了一个通用的参数化混合猜测的框架.该框架可以混合不同数据驱动方法的猜测优势以生成更高效的猜测集.该框架由2部分构成：模型剪枝和最优猜测数分配.模型剪枝可以确保框架中的每个方法仅生成自身擅长猜测的口令，从而避免与其他方法生成重复口令；而理论证明最优的猜测数分配方案可以确保不同方法生成指定猜测数的口令时，框架的整体猜测效率将达到最优.

为了验证框架的通用性和最优性，本文也基于该框架进行了猜测实践.本文分析了现有数据驱动的口令猜测方法的猜测优势，并根据分析结果将具备不同猜测优势的方法作为框架的组成模块，设计了多个混合不同猜测模型的参数化混合口令猜测方法(parameterized hybrid password guessing Method, hyPassGu).实验评估结果显示，不同方法组合构建的hyPassGu均超越了单一方法的猜测效率，验证了框架的通用性.而和其他猜测数分配方案的比较结果也证实了框架中猜测数分配方案的最优性.

本文的主要贡献有2个方面：

1) 提出了一个能够结合不同数据驱动方法猜测优势的通用参数化混合猜测框架.在该框架中，本文通过分析数据驱动方法的猜测模型，提出了模型剪枝的通用方案.此外，为了保证框架整体猜测效率的最优，本文提出并在框架中应用了理论证明最优且适用多个方法的猜测数分配策略.

2) 基于框架和对现有数据驱动方法的优势分析，提出了组合不同方法的多个参数化混合猜测方法(统称为hyPassGu)，并通过对这些方法猜测效率的评估实验验证了框架的通用性和最优性.实验结果表明，不同方法组合构建的hyPassGu均表现出超越单一方法的猜测效率，在1010猜测数下超越了单一方法最优效率的1.52%～35.49%.并且，相较于单一方法的最优效率，hyPassGu与Min_auto的差距相对缩短了16.78%～63.99%.此外，实验结果还表明，最优分配策略的猜测表现稳定优于平均分配策略和随机分配策略，并在108猜测数下在离散程度最大的数据集上有16.87%的相对提升，同时更多元的混合方法整体表现出更好的猜测效率.这些结果进一步验证了框架的通用性和最优性.

1 相关工作

1.1 数据驱动猜测方法的优化

在过去的数十年里，研究人员致力于改进现有数据驱动猜测方法在猜测某些口令时的不足，以此来提高方法的猜测效率.

对于PCFG方法，Veras等人[13]利用自然语言处理算法提取分析口令中的语义模式，增强了模型对于字母字符串的泛化能力，使得模型可以生成更多可能的字母字符串.Houshmand等人[8]通过引入更多的口令结构模式来更细粒度地定义口令中的结构，增强了模型对于结构的泛化能力.Li等人[11]引入了拼音字典来弥补模型在中文口令破解方面的不足.韩伟力等人[15]通过裁剪PCFG模型的搜索空间并引入变形的方式，来生成与样本口令高度相似的模拟口令.邹静等人[16]则是根据用户习惯来2次划分高概率结构，以解决高概率结构只能生成少量口令的问题.

对于Markov方法，Ma等人[12]提出了Markov模型的变种，即n阶Markov模型，来增强Markov模型对上下文信息的利用能力.这里的n指的是用来推测下一个字符出现概率的连续字符数量.此外，他们还提出了用变阶Markov模型，即Backoff来解决高阶Markov模型存在的数据稀疏问题.与n阶Markov模型不同，Backoff会选择出现频率达到预设阈值的尽可能长的字符串来推测下一个出现的字符，以此在尽可能利用上文信息的同时避免数据稀疏的问题.

不同于已有研究对单一方法的改进思路，本文提出的参数化混合猜测旨在最大化利用多个数据驱动猜测方法各自不同的猜测优势，即利用不同方法的优势来弥补各自的不足.

1.2 现有猜测方法中的混合猜测实践

现有的猜测方法中，一些方法已经实现了混合猜测的简单实践，如Hashcat[19]和PCFGv4.1[20].

Hashcat中的混合攻击模式实际上是一种组合攻击.它将字典攻击和其他诸如暴力攻击、掩码攻击的攻击方式相结合，既发挥了字典中单词常被用户使用的优势，又利用其他攻击方式来扩展字典攻击的搜索空间，提高了猜测效率.以字典攻击和暴力攻击相结合的方式为例，暴力攻击所能生成的字符串可以作为字典中每一个单词的前缀或者后缀.换句话说，如果使用暴力攻击来为单词添加1个数字作为后缀，那么根据单词“hello”可以得到“hello0”到“hello9”的猜测口令.

PCFGv4.1则是设计了一个可选的参数“coverage”来控制基于Markov模型的暴力生成方法的使用.这个想法尝试使用暴力生成方法来扩展模型的搜索空间，从而提高猜测效率.但是，该工作缺乏对PCFGv4.1和Markov模型的深入分析，因而不能最大程度地利用每个方法的独特优势.

此外，也有一些研究工作对猜测集的混合进行了相关探索.Parish等人[21]通过计算不同猜测方法生成的口令之间的相似性及互补性、利用不同方法的互补性进行混合猜测实验，进而提升混合猜测集的破解效率.汪定等人[22]则通过利用循环神经网络(recurrent neural network，RNN)、LSTM分别和PCFG，Markov，PR模型组合生成猜测集的方法，首次证实了在相同猜测数下，组合不同类型模型所产生口令猜测集的破解率通常高于单一猜测集.这些研究工作对猜测集的混合做了一定探索，但缺乏针对猜测集的高效混合策略的系统分析和考虑，如利用不同方法的优势互补而非简单的互补来提高猜测集的有效性.

相较于已有工作在猜测集混合方面的探索，本文从优势互补的角度出发，通过理论分析和证明提出了针对数据驱动猜测方法的通用的参数化混合猜测框架，并基于该框架和现有的数据驱动猜测方法进行了猜测实践，实现了高效的参数化混合猜测.

2 参数化混合猜测框架

为了在有限的猜测数内最大化地利用不同方法的猜测优势，本文提出了如图1所示的参数化混合猜测的框架.该框架具体分为2个部分：模型剪枝和最优猜测数分配.其中模型剪枝是为了让不同猜测方法在发挥自身猜测优势的同时避免生成彼此重复的猜测口令，从而提高猜测数的利用率；而最优猜测数分配是为了在总猜测集的数目确定的情况下，通过调整不同猜测方法的可用猜测数(即图1中的k1～kn)，使得总猜测集的猜测效率最优.下面将介绍这2个部分的做法.

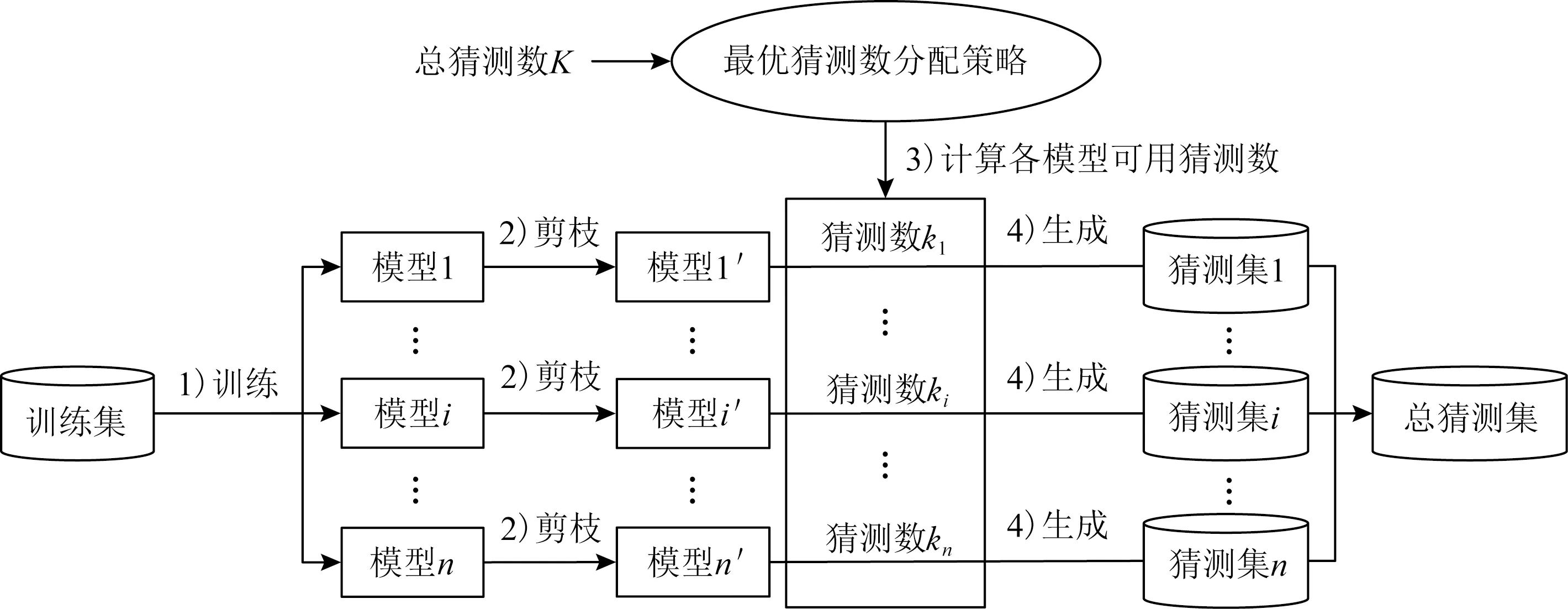
Fig. 1 Framework of parameterized hybrid password guessing图1 参数化混合口令猜测的框架

2.1 模型剪枝

数据驱动的猜测方法是基于训练集训练出的生成模型，一般可以看作1棵树，其中每个叶子节点对应的是1条猜测口令，而从根节点到叶子节点的路径则可以看作该猜测口令的生成路径.模型生成1条口令的过程就是从根节点查找到该口令对应的叶子节点的路径，而这条路径上的中间节点表示的是组成该口令的字符串片段以及对应的概率.如果某条口令对应的生成路径缺失了部分节点，那么模型从根节点将无法找到该口令对应的叶子节点，也因此不会生成出这条口令.

Fig. 2 Example of model pruning of data-driven password guessing methods图2 数据驱动的口令猜测方法的模型剪枝示例

如图2所示，将数据驱动的生成方法抽象成1棵生成树，其中Si表示生成过程中的1种状态，不同的下标数字表示不同的状态.在数据驱动的生成方法中，Si可以指代口令的上下文信息(如Markov模型使用的上下文字符)、口令的结构或者口令结构的内容实例(如PCFG模型使用的口令结构和结构对应的具体实例).

从起始符开始，生成模型将根据生成过程的上一状态选择下一状态，直到遇到终止符为止.图2中删除了从状态S1到状态S4的转移路径，有2条生成路径将受此影响而无法正常生成猜测口令，因此图2中的生成方法最终只能生成由状态S1S2S3和S5S4S6构成的2条猜测口令.

通过删除一些不必要的生成路径，模型将只保留其擅长猜测的口令所对应的生成路径，而不同模型擅长猜测的口令互不相同，这就可以保证不同模型将不会生成重复的猜测.删除生成路径的做法就是模型剪枝，具体的实现方式是把生成路径中的某个不影响其他路径的节点删除，即将该节点对应的字符串片段和相应的转移概率从模型中移除.

2.2 最优猜测数分配

通过建立概率猜测方法猜测口令，破解数与猜测数之间关系的数学模型，本节提出了2个引理和1个定理来探寻最优的猜测数分配方案.该方案是基于理想攻击场景提出的，即训练集与测试集具有相同的分布.这类攻击场景也被称为站内猜测(intra-site guessing)，被研究者们广泛采用[8,11,22-25].此外，考虑到大猜测数的情况下训练集的限制会导致概率猜测方法出现瓶颈，即破解口令数不再增长，本文在本节中仅分析概率猜测方法尚未达到破解瓶颈时的情况，并将在4.5节的实验评估中讨论大猜测数对分配方案的影响.

随着猜测数的增长，一个概率猜测方法破解出的口令数也会增长，也就是说它的“破解数-猜测数”曲线是一条单调递增的曲线(曲线上的点的横坐标表示使用的猜测数，纵坐标表示破解口令数).由于概率猜测方法会优先猜测概率更高的口令，而更高的概率往往意味着猜测方法认为该口令在测试集中出现的频率也更高.这带来的结果就是小猜测数下单次命中能破解的口令数要多于大猜测数下单次命中能破解的口令数.换句话说，单位猜测数里被猜中的口令数会随着猜测数的增长而减小，即“破解数-猜测数”曲线的一阶导数逐渐变小，最后趋近于0.因此，一个概率猜测方法的“破解数-猜测数”曲线可以看作一个单调递增的凹函数(凹函数的二阶导数小于0，即一阶导数单调递减).

基于上述数学模型，最优的猜测数分配策略的目标是在不同概率方法的“破解数-猜测数”曲线上分别寻找1个点，使得所有点的横坐标的和为定值时，纵坐标的和是所有组合情况中的最大值，此时每个概率方法曲线上的点对应的横坐标就是被分配的可用猜测数.引理1证明了上述目标在概率方法仅有2个时的等价条件，定理1则是将等价条件拓展到n个方法的情况.

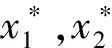
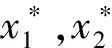
(1)

(2)

(3)

(4)

(5)

证毕.

n≥2且n为整数.

证明.可以利用数学归纳法来证明该定理.首先，根据引理1，定理1在n=2的时候成立.接着，假设定理1在n=k(k≥2且k是个整数)的时候成立.那么当n=k+1的时候，对于k+1个点中的任意k个点，定理1成立.换句话说，当固定k+1个点中的任意1个点，然后寻找其他k个点的纵坐标和为最大值的情况时，这k个点的一阶导数一定相同.更进一步，固定k+1个点中的其他任意点，再重复上述操作，可以发现k+1个点的一阶导数的值会趋于相同，最终可以得到k+1个点的纵坐标和为最大值的条件是这k+1个点的一阶导数都相同.与引理1中式(2)到式(1)的推导类似，k+1个凹函数组成的函数的二阶导数也小于0，这意味组成的函数也是凹函数，所以找到的局部最大值也是全局最大值.

证毕.

由引理1和定理1可知，最优猜测数分配策略应当找到不同概率方法的“破解数-猜测数”曲线上一阶导数相等的点，即单位猜测数内破解口令数相等的点.文献[26]表明口令数据集的分布符合Zipf定律，即将口令按照在数据集中出现的频率降序排序之后，口令出现频率的lg值和口令排名的lg值满足式(6).基于该定律，对于理想的猜测方法(每次猜测能破解出剩余口令中概率最高的口令)而言，其每次猜测破解的口令数目的lg值(即式(6)中的lgy)和已经使用的猜测数的lg值(即式(6)中的lgx)满足：

lgy=lgC-α×lgx.

(6)

尽管实际的概率猜测方法不能保证每次猜测都能够破解出1条口令，但在总体趋势上满足了优先猜测概率更高(出现频率也更高)的口令，因此可以假设概率猜测方法在单位猜测数内所能破解的口令数目的lg值和已经使用的猜测数的lg值也满足式(6).此外，同一数据集内不同猜测方法的α值会在该数据集Zipf分布的α值周围扰动，因此可以看作近似相同.本文也将在第3节的应用实践中通过实证实验来验证该假设的相关性质.

基于上述假设，引理2证明了不同猜测方法曲线上一阶导数相等的点的横坐标与数据集中口令分布的等价关系.

证明.这2条单位猜测数内破解口令数曲线可表示为lgy1=lgC1-α×lgx1和lgy2=lgC2-α×lgx2.

这里引入了口令类别的概念来泛化各个方法的猜测优势，这样做一方面可以避免过拟合，使得方法的猜测优势不局限于特定数据集的特定口令，另一方面也可以利用训练集和测试集的同分布特性，基于训练集中的口令分布提前为框架中的各个方法分配猜测数.

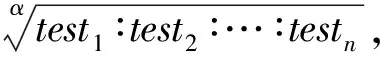
3 参数化混合猜测方法

基于第2节提出的框架，本节将现有的数据驱动猜测方法应用到框架中来设计实际可用的参数化混合猜测方法，具体步骤分为：优势分析、模型剪枝和猜测数分配.为方便表示，这些参数化混合猜测方法统称为hyPassGu.

3.1 数据驱动方法的优势分析

本节将口令根据其构成字符种类分为7类：仅由字母构成、仅由数字构成、仅由特殊符号构成、由字母和数字构成、由字母和特殊符号构成、由数字和特殊符号构成、由3种字符一起构成.接着，本节量化比较了现有的概率猜测模型在不同类别的口令上的猜测效率，并分析了其优势背后的方法原理.为了衡量模型生成新的有效口令的能力，实验将数据集按3∶1的比例拆分成训练集和测试集，并从测试集中去除了在训练集中出现的口令来计算猜测效率.本节选取了中文数据集CSDN和英文数据集Rockyou来进行分析实验，以此探究各模型在这两种数据集上的猜测优势规律.

根据图3展示的结果，这些概率方法在不同类别的口令上表现差别很大.

3阶Markov(Markov-3)在猜测仅由字母构成的口令上整体表现最优，在CSDN数据集上优于其他方法，在Rockyou数据集上略逊于Semantic PCFG；4阶Markov(Markov-4)在猜测仅由数字构成的口令上整体表现最优，在CSDN数据集上优于其他方法，在Rockyou数据集上略逊于Backoff；而在猜测仅由特殊符号构成的口令上则是Backoff和2阶Markov(Markov-2)分别在CSDN和Rockyou数据集上表现最优.Markov模型在1类字符构成的口令上的优异猜测效果表明， 口令中使用的连续同类字符之间的关联会更加紧密，因此使用多个连续同类字符来预测下一个同类字符会很有效.并且，相较于使用连续出现的字符预测下一个出现的不同类的字符，预测同类的字符需要的搜索空间更小，这也会帮助模型达到更准确的预测效果.一般而言，更高的阶数会使得Markov模型的猜测效率更好，但过高的阶数也会造成过拟合的问题.例如，图3中的6阶Markov模型就表现出了严重的过拟合问题，导致其在各类口令上的猜测效果都不佳.

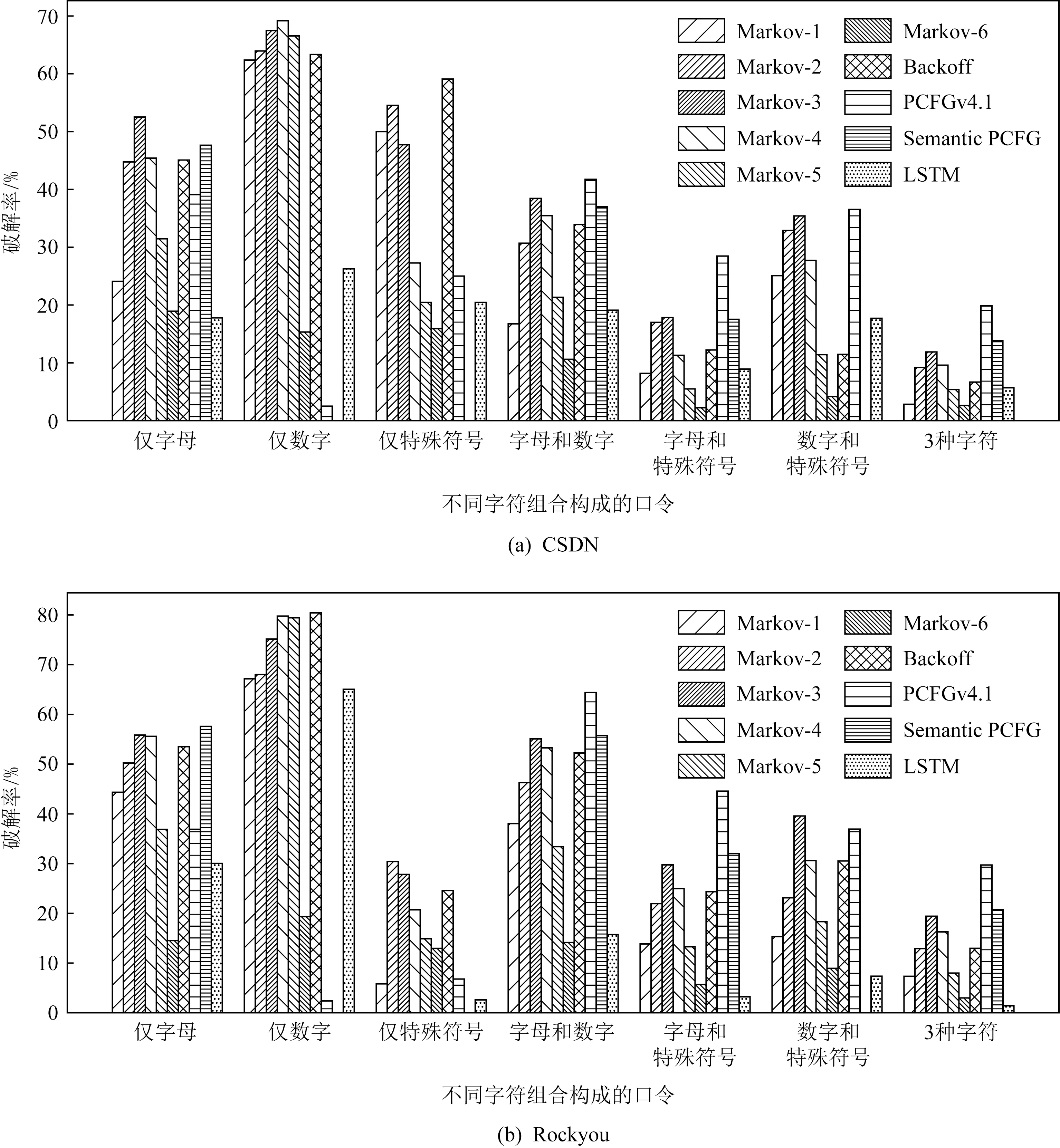
Fig. 3 Guessing efficiency of single method on different types of passwords under 1010 guesses图3 1010猜测数下单一方法在不同类别口令上的猜测效率

PCFGv4.1在猜测2类及以上字符构成的口令方面表现几乎均优于其他方法，除了在Rockyou数据集的数字和特殊符号构成的口令上表现略逊于3阶Markov，这是因为PCFGv4.1引入了多词模式、键盘模式、上下文模式和年份模式来更细粒度地区分口令的结构，从而使得模型在猜测2类及以上字符构成的口令时，一方面能生成更多可能的组合，另一方面也能减少一些不必要的搜索空间来提高猜测效率.其中，多词模式根据单词出现的频率将连续的长字母串分成多个单独单词来表示结构，可以丰富长字母串的组合情况；键盘模式将识别出的键盘上的连续输入看作特定的键盘结构，可以减少模型针对数字、字母、特殊符号混杂的键盘串的不必要搜索；上下文模式识别常见的特殊符号和字母数字的组合来作为特定结，如“<3”，“:p”这些类似表情的输入，也是对不同类字符混杂字符串搜索空间的减少；而年份模式则是把单独出现的连续4个数字中符合要求的数字识别为年份，这种更细粒度的类别标签可以减少年份串和其他字符串组合时的搜索空间.

总的来说，现有的概率猜测模型中，Markov模型(1～5阶、Backoff)在猜测仅由1类字符构成的口令方面表现明显优势，而PCFGv4.1在猜测2类及以上字符构成的口令方面表现优于其他方法，两者互补的优势为后续参数化混合猜测方法的设计提供了便利.而Markov-6、Semantic PCFG和LSTM则没有表现出明显的猜测优势，因此不在混合猜测方法设计的考虑范围之内.

3.2 hyPassGu的模型剪枝

了解到不同方法的猜测优势后，需要通过模型剪枝来限制各方法生成的口令.剪枝方法参照了2.1节的介绍，本文将以Markov模型和PCFGv4.1模型为例，结合2.1节的样例介绍具体的做法.

根据3.1节的优势分析结果，Markov模型应当仅生成1类字符构成的口令，比如“password”这种仅由小写字母构成的口令，因此需要对其模型剪除2类及以上字符构成的口令的生成路径；PCFGv4.1模型则与之相反，需要剪除1类字符构成的口令的生成路径.

Markov模型的生成方法依赖上文的字符内容来预测下一个要生成的字符，对照图2中的示例可知，状态Si在Markov模型中表示上下文的字符.以1阶Markov模型为例，口令“abc”的生成路径为“起始”-“起始a”-“ab”-“bc”-“c终止”.通过观察可以发现，在1类字符构成的口令所对应的生成路径中，所有的状态都仅包含1类字符，而2类及以上字符构成的口令中至少存在1段路径的状态包含多类字符，因此只需要从Markov模型中删除包含多类字符的状态转移路径，就可以剪除2类及以上字符构成的口令的生成路径.在实际的实践中，通过限制训练集为仅包含1类字符构成的口令，来使得Markov模型统计的状态转移只包含同类字符之间的情况，从而保证Markov模型仅能生成1类字符构成的口令.

PCFG模型的生成方法与Markov模型略有不同，它的状态分为2类：一类是口令结构、一类是结构的具体内容实例.举例来说，口令“abc123”的生成路径为“起始”-“L3D3”-“abcD3”-“abc123”-“终止”.通过观察可以发现，在起始符到口令结构的选择这一步，PCFG模型通过口令结构就可以知道最终生成的口令将包含几类字符，因此通过删除1类字符构成的口令所对应的口令结构，模型将只能生成2类及以上字符构成的口令.在实际的实践中，对于PCFGv4.1训练得到的口令结构文件进行分析，去除了其中仅由1类字符构成的口令结构，并对剩余的口令结构概率做了归一化处理.具体来说，本文去除了仅由“A”(英文字母)、“D”(数字)、“O”(特殊符号)、“Y”(年份，纯数字)中的某一类标签组成的口令结构.

3.3 hyPassGu的猜测数分配

在对hyPassGu中的模型剪枝后，参照2.2节中的最优猜测数分配策略，本节将验证式(6)，并探究在实际数据集上α取值的情况.以108作为单位猜测数，本节使用式(6)来拟合实际的猜测方法.

表1展示了CSDN数据集上的拟合结果.PCFGv4.1方法破解情况线性拟合的决定系数R2=0.99，Markov方法破解情况线性拟合的决定系数平均为0.75左右，这意味着大部分数据点符合回归曲线.

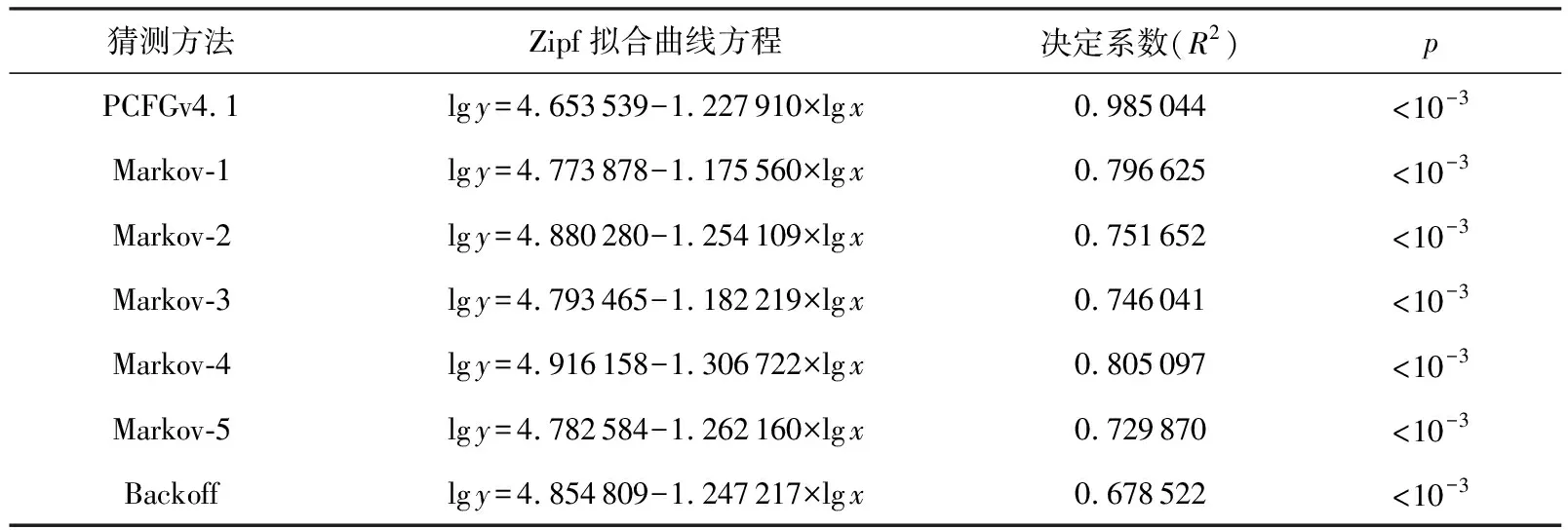
Table 1 Fitting Results of Zipf’s Law Based on CSDN

此外，p值检验的结果显示所有的p<10-3，这意味着回归曲线的系数可以很好地表示数据点.不同方法在CSDN数据集上拟合结果的系数α值都很接近，集中在1.2和1.3左右.此外，本文基于Rockyou数据集的拟合结果与基于CSDN数据集的拟合结果相似，系数α值也集中在1.2和1.3左右.基于这些结果，本文推荐使用1.2和1.3作为最优猜测数分配策略中α的值.

4 实验与评估

基于第3节的方法设计，本节通过实验评估不同配置下的hyPassGu的猜测效率，以此验证框架的通用性以及猜测数分配策略的最优性.此外，还探究了猜测数大小和口令数据集离散程度对分配策略的影响，并讨论了混合方法种类数对猜测效率的影响.

4.1 数据集

如表2所示，本文在实验中使用了4个从真实网站泄露的大规模口令数据集：CSDN[27]，Youku[28]，Rockyou[29]，Neopets[30].其中，CSDN和Youku的数据集泄露自中文网站，而Rockyou和Neopets的数据集泄露自英文网站.此外，CSDN和Rockyou数据集是2011年之前泄露的，Youku和Neopets数据集则是近6年泄露的.这些数据集在区域跨度和时间跨度上都颇具代表性，并且在先前的研究[11-12,14,23-25]中被研究人员广泛使用.

为了尽可能保证本文实验中使用的数据是真实用户创建的口令，本文参照先前的研究[12]，从数据集中清理了包含非可打印ASCII码的口令和长度超过32的口令，最终本文从4个数据集中获取了共计超过1.5亿条的口令数据.

Table 2 Basic Information of Password Datasets

本节实验中的数据集均按3∶1随机拆分为训练集和测试集，并且为了衡量模型生成新的有效口令的能力，测试集中去除了训练集中出现过的口令后来计算猜测效率.

4.2 模型剪枝后的优势评估实验

根据3.1节分析得到的结论，本节按照3.2节介绍的方法对Markov模型(1～5阶、Backoff)和PCFGv4.1这7个模型进行剪枝，并评估了各模型在剪枝后对其擅长猜测口令的破解率相较于剪枝前的提升幅度.评估结果如表3所示，各模型在剪枝后，在其擅长猜测口令上的破解率相较于之前均有不同程度的相对提升(0.24%～54.45%)，验证了剪枝方案的有效性.

Table 3 Relative Improvement of Guessing Advantages After Model Pruning Under 1010 Guesses

4.3 二元hyPassGu的评估实验

1) 实验配置

本节选取了6对存在不同优势的概率模型，即PCFGv4.1和6种不同的Markov模型(Backoff和1～5阶Markov模型).模型剪枝后，PCFGv4.1将只能生成2类及以上字符构成的口令，而Markov模型将只能生成1类字符构成的口令.图4展示了组合不同猜测方法的二元hyPassGu在CSDN数据集上的猜测效果，其中每张子图里的Min_auto曲线使用的模型为该子图中对应的2个单一方法.

2) 实验结果

如图4所示，二元hyPassGu的猜测效率相较于单一方法提升了1.52%～35.49%.其中，优势差异越明显的2个方法，在参数化混合之后的猜测效率提升就越大，但想要获得更高的总破解效率，则需要结合优势更强的方法.

Fig. 4 Guessing efficiency of binary hyPassGu compared with that of other methods based on CSDN图4 基于CSDN数据集二元hyPassGu与其他方法的猜测效率

具体来说，1阶Markov在猜测仅由数字构成的口令上表现远优于PCFGv4.1，而PCFGv4.1在猜测2类及以上的字符构成的口令上表现远优于1阶Markov，因此两者的优势结合后猜测效率的相对提升达到了35.49%；而对于3阶Markov和4阶Markov而言，它们在猜测2类及以上字符构成的口令上不如PCFGv4.1表现优异，但与PCFGv4.1的差距相较于1阶Markov来说要小很多，因此优势结合后猜测效率的相对提升也要少一些.但是，鉴于3阶Markov和4阶Markov在猜测1类字符构成的口令上更强的优势，将它们与PCFGv4.1结合可以在总的破解率上达到更高，即达到49.88%和49.92%的破解率.

此外，与多模型结合的理想上界Min_auto相比，二元hyPassGu与它在猜测效率上的差距控制在5.22%～6.68%.相较于单一方法的最优效率与Min_auto的差距，二元hyPassGu将差距缩短了16.78%～63.99%.

4.4 三元hyPassGu的评估实验

1) 实验配置

本节选取3阶Markov、4阶Markov和PCFGv4.1来设计三元hyPassGu.考虑到仅由特殊符号构成的口令在现有的真实口令集中的占比不到0.1%，难以针对这类口令单独分配猜测数，因此由3阶Markov来猜测仅由特殊符号构成的口令.各模型的猜测任务具体为：3阶Markov猜测仅由字母构成和仅由特殊符号构成的口令；4阶Markov猜测仅由数字构成的口令；PCFGv4.1猜测2类及以上字符构成的口令.在4个数据集上的评估实验结果如图5所示，其中Min_auto曲线中使用的模型为3阶Markov、4阶Markov和PCFGv4.1.

2) 相较于单一方法的猜测效率提升

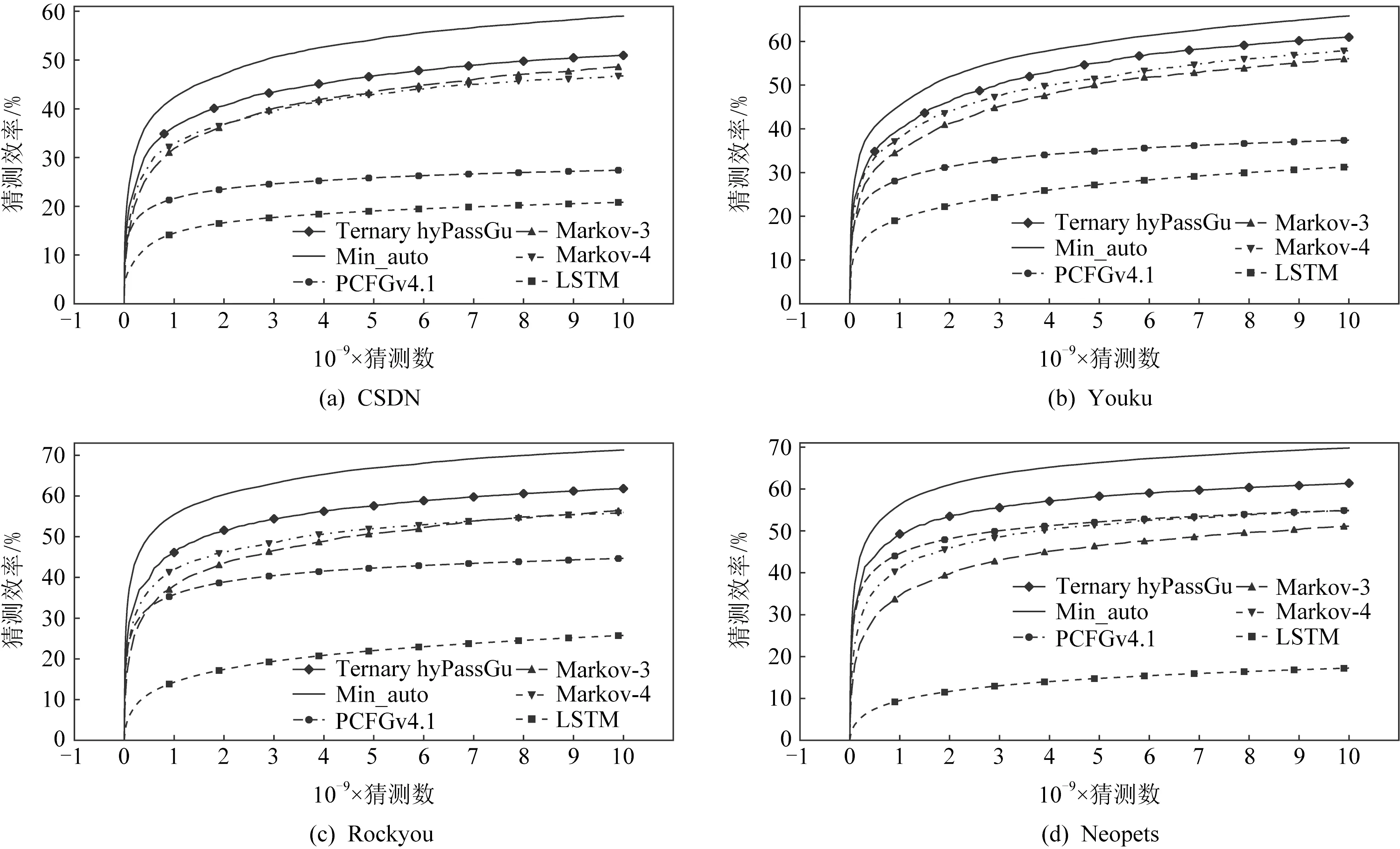
Fig. 5 Guessing efficiency of ternary hyPassGu compared with that of other methods图5 三元hyPassGu与其他方法的猜测效率的比较

如图5所示，在4个数据集上的评估实验表明，三元hyPassGu在1010猜测数下的猜测效率超越单一猜测方法的最优猜测效率4.55%～11.58%.不同数据集上单一方法的表现各有优劣，其中在CSDN数据集上3阶Markov表现最优，在Youku数据集上4阶Markov表现最优，在Rockyou数据集上，3阶Markov和4阶Markov表现最优，而在Neopets数据集上，PCFGv4.1和4阶Markov表现最优，而相比之下，结合了不同方法猜测优势的三元hyPassGu在4个数据集上均表现出相较于单一猜测方法猜测效率的稳定提升.

此外，相较于单一方法的最优效率，三元hyPassGu与Min_auto猜测效率的差距缩短了22.54%～43.19%.

3) 不同猜测数分配策略的比较

本节利用4个数据集上不同策略的比较实验来验证2.2节提出的最优猜测数分配策略的最优性.

如表4所示，第1列表示数据集，第2列和第3列表示不同α取值的最优猜测数分配策略下的三元hyPassGu的猜测效率，第4列表示平均分配策略(即混合方法中每个方法使用的猜测数一样)下的三元hyPassGu的猜测效率，第5列表示1 000组随机分配策略下的三元hyPassGu的平均猜测效率，第6列表示在实际的破解实验中三元hyPassGu能达到的最优性能.为了找到三元hyPassGu的实际最优性能，需要比较模型在所有可能配置下的性能.以1010猜测数为例，需要使用PCFGv4.1、3阶Markov和4阶Markov各自生成1010条猜测口令，然后遍历总数为1010的所有可能的组合，最终找到能猜测出最多数量口令的组合并把它的表现作为hyPassGu的最优性能.

从表4中可以看出，不同α值对猜测效率的影响很小，整体来说α=1.2时猜测效率更好.最优分配策略下的三元hyPassGu表现远优于随机分配策略下的三元hyPassGu，超出了7.60%～17.05%.此外，最优分配策略下的三元hyPassGu的猜测效率与实际最优性能的差值在0.07%～0.42%之间，而平均分配策略下的三元hyPassGu的猜测效率与实际最优性能的差值是上述差值的3.6～8.7倍.上述差值表明最优分配策略的可提升空间很有限，因此可以认为本文提出的猜测数分配策略是最优的.

Table 4 Guessing Efficiency of Ternary hyPassGu with Different Allocation Strategies Under 1010 Guesses

4.5 最优猜测数分配策略的探究实验

鉴于表4中最优分配策略在1010猜测数下相较于平均分配策略并没有明显的猜测效率优势(尤其在CSDN和Rockyou数据集上)，本节利用蒙特卡洛方法[31]进一步探究了猜测数大小和口令数据集离散程度这2个因素对最优猜测数分配策略的影响.其中，根据已有研究[8,11,13,18,21-25]常用生成离线口令猜测集的大小，本节选取了108～1014作为猜测数的范围；另一方面，本节使用各特征的口令占比计算得到的标准差(standard deviation, SD)作为口令数据集离散程度的度量指标.

实验结果如表5所示，第1列表示数据集，第2列表示各数据集中不同特征口令占比计算得出的标准差(该值的大小反应了数据集中不同特征口令分布的离散程度，值越大，数据集口令分布越不均匀)，第3，6，9，12列表示各猜测数下平均分配策略的猜测效率，第4，7，10，13列表示各猜测数下最优分配策略的猜测效率(根据4.4节的结果，α=1.2)，第5，8，11，14列则表示最优分配策略相较于平均分配策略的相对提升.

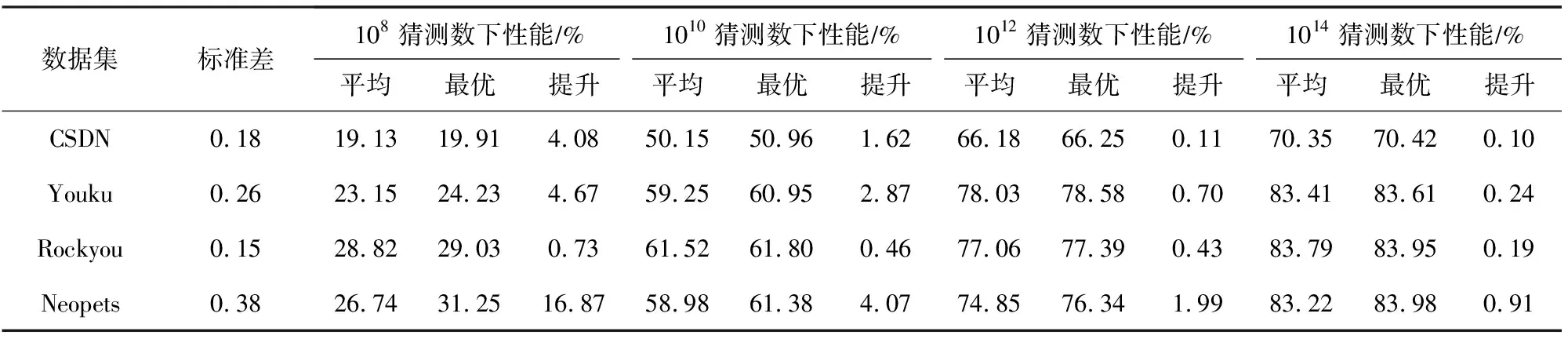
Table 5 Performance Improvement of Optimal Allocation Strategy Under Different Guesses when α=1.2

Fig. 6 Improvement of the best performance of ternary hyPassGu compared with that of binary hyPassGu图6 三元hyPassGu相较于二元hyPassGu最优效率的提升

1) 猜测数大小对最优分配策略的影响

如表5所示，在108猜测数下，最优分配策略相较于平均分配策略的提升效果最好，平均相对提升6.59%.而当猜测数在108～1014之间时，最优分配策略相较于平均分配策略的提升效果逐渐降低，原因是随着猜测数的增长，概率方法由于训练集的限制逐渐达到瓶颈，破解数将不再增长，不同分配策略的效率差距也因此减小.

2) 数据集的口令离散程度对最优分配策略的影响

如表5所示，通过对比可以发现，最优分配策略相较于平均分配策略的提升效果与标准差值呈正相关，即标准差值越大，数据集口令分布越不均匀、最优分配策略的猜测优势越明显.其中，Neopets数据集的离散程度最高，最优分配策略带来的提升也最明显，在108猜测数下提升可以达到16.87%.这是因为当标准差值较小、数据集中对应特征的口令分布趋于平均时，最优分配策略将采取和平均分配策略基本一致的分配方案，两者猜测效率也将相似.

4.6 混合方法种类(元数)对破解效果的影响

本节通过对比分析三元hyPassGu和二元hyPassGu的猜测效率，讨论混合方法种类数(元数)对破解效果的影响.图6中的横坐标表示使用的猜测数(考虑到最优分配策略发挥作用的猜测数区间，这里也选取了108～1014作为猜测数的范围)，纵坐标表示的是三元hyPassGu相较于二元hyPassGu中最好的猜测效率的相对提升.其中，三元hyPassGu混合的是PCFGv4.1、3阶Markov和4阶Markov，而二元hyPassGu分别混合的是PCFGv4.1和3阶Markov，以及PCFGv4.1和4阶Markov.

从图6可以看出，三元hyPassGu相较于二元hyPassGu整体表现更好，有一定的猜测效率提升，而在较大猜测数下(1012～1014)，三元hyPassGu和二元hyPassGu的猜测效率趋于相同.这一点与最优分配策略的提升表现一致，意味着概率方法在大猜测数下的破解瓶颈也导致了更多元的混合方法在大猜测数下并未有明显的猜测效率提升.

5 讨 论

1) 更多元的混合猜测方法

随着口令猜测方面研究的发展，优化的猜测方法甚至全新的方法，例如基于表征学习的方法[22]正不断被提出.将一个新的口令猜测方法结合到本文提出的框架中有以下2种情况：①如果它根据概率降序生成候选口令，参考本文第3节的步骤就可以尝试将它结合到框架中.②如果它随机地生成候选口令需要先引入口令的概率计算和排序，例如，表征学习的采样方法[22]，而这是我们未来的工作方向.

此外，本文在分析基于深度学习技术的口令猜测方法LSTM时发现其没有相较于其他方法独有的猜测优势，因此在实现混合方法时并未结合基于深度学习的口令猜测方法.在未来的研究中，可以考虑利用迁移学习等技术来提高深度学习方法在特定类型口令上的猜测效率，并且在改进PCFG等传统方法时也可从强化已有猜测优势的角度入手，进一步提高这些概率方法的优势猜测能力，从而使得多元混合方法在大猜测数下(1012以上)也能有更好的猜测表现.

2) 最优猜测数分配策略的可能偏差

猜测数的最优分配策略可能会由于以下一些步骤导致一些偏差：首先，当使用Zipf定律去拟合不同猜测方法单位猜测数内破解的口令数时，Markov方法的决定系数R2<0.9，这意味着拟合结果不能很好地解释所有的原始数据.其次，单位猜测数内破解的口令数的积分值被近似为目标集的大小是很理想的近似，而实际的曲线积分值会小于目标集的大小.尽管这些可能的偏差会导致最优分配策略和实际最优性能的差距，但是第4节的实验评估结果显示两者的表现非常接近，并且可供继续优化的空间也很有限.此外，分配策略中α值的选择依赖于实证分析的结果，但是4个数据集上的良好表现也表明α值的选择可以看作是通用的.

6 总 结

本文提出了一个能够在有限猜测数内充分利用不同方法的猜测优势来高效地生成口令的参数化混合猜测的框架.基于现有的数据驱动猜测方法，本文通过分析它们的猜测优势并组合不同方法来构建实际可用的参数化混合猜测方法.评估结果表明，不同方法组合构建的参数化混合猜测方法均表现出超越单一方法的猜测效率，验证了框架的通用性.在1010猜测数下，参数化混合猜测方法超越了单一方法的最优效率1.52%～35.49%，且最优猜测数策略配置下的参数化混合猜测方法表现均优于其他策略配置下的参数化混合猜测方法.此外，相较于单一方法的最优效率，参数化混合猜测方法与Min_auto理想值的差距相对缩短了16.78%～63.99%.不同猜测数下的实验结果还表明，最优分配策略的猜测表现优于平均分配策略和随机分配策略，并在108猜测数下，在离散程度最大的数据集上有16.87%的相对提升.这些结果进一步验证了框架的最优性.

本文的实验结果与分析充分说明了结合不同概率模型的猜测是比单一猜测方法更高效的生成口令猜测集的方式.在接下来的工作中，我们将尝试将更多的猜测方法结合到本文提出的混合猜测框架中.我们还将引入不同的口令分类方案，例如根据口令长度分类，更加深入挖掘数据驱动方法的猜测优势.此外，我们还将研究动态调整框架中不同方法可用猜测数的方案.

作者贡献声明：韩伟力负责提出混合不同猜测方法优势的研究方向和算法思路，以及文章整体架构的设计和修改；张俊杰负责参数化混合猜测方法hyPassGu的设计和改进，以及全文内容的撰写；徐铭负责全文内容表达的修改，以及hyPassGu改进思路的讨论和补充；王传旺和张浩东负责完成hyPassGu和其他方法的对比实验，以及文章定理的验证；何震瀛和陈虎负责文章整体思路的指导，以及文章内容的修改.