松散式多源输入稳定并网监测系统的仿真

李瑜 王德志

包头职业技术学院 内蒙古包头 014030

本课题开展的基于松散式多源输电稳定并网的研究，主要是实现对松散式多输入源并网接入过程中，输入源监测与干扰定向进行研究，实现了一套可以实时动态监测松散式多源输电稳定性系统，并基于MATLAB完成了对多源输电稳定并网的实验分析。

1 负荷非线性程度与干扰源定位方法

1.1 已有的多源输入并网中的干扰源定位的方法

目前在大部分文献中研究输入为多源的并网系统的干扰源头集中在谐波源定位上，最让人熟知的研究方法是谐波功率流向法，但该研究方法还是有一定的缺陷。因此在松散式多电源并网系统的研究中，我们把输入信号当作电网的负载，通过对电力系统的负载进行研究和理论分析来对多输入信号进行研究和分析。

负载曲线和负载特性是电力系统负载运行当中两个重要指标，负载曲线和负载特性的定义指的是，负载功率随着时间的增加或减少变化的规律，负载特性根据电力系统运行状态分类可以分为静态特性和动态特性，根据负载功率类别的不同又分为有功功率特性和无功功率特性。下面我们来具体解释，首先我们先负载特性指的是负载功率随着频率和电压的递增或递减发生变化的曲线规律，在这里我们要知道负载特性是由两方面组成的，就是上面我们提到的负载功率随电压的变化和频率的变化的规律。负载的电压特性以及负载的频率特性又是由动态和静态特性构成的。所谓“静态”指的是当电力系统中电压或者频率信号达到稳定时，这时候负载和电压、频率信号的关系称为静态特性，“动态”顾名思义就是当电压或者是频率信号没有进入稳定状态前，还在发生变化式的状态，这时负载功率随着电压、频率这两个输入信号的关系称之为动态特性，根据负载特性以上几个分类，我们要总结分析以上特性，才可以更准确、更好地分析该系统中负载的特性。

当我们分析处在稳定状态的电力系统时，负载的数学模型可以用无功功率和有功功率来表示，一般来说负载的静态特性计算精度比较高，所以在精度要求比较高的场合采用的是负载静态特性。

本文在研究中主要是研究松散式多源输电稳定性的问题，当该系统存在多源输入，在该系统并网的过程中，需要对该系统多源输入的负载进行精准的分析和定位。因此，在研究中我们将选用负荷模型及相关理论来对多源输入系统在并网过程中的稳定性及干扰源进行分析，已达到快速地分析多源输电并网过程中的扰动，并对其进行定位的目的。

1.2 多输入源并网过程中非线性程度分析与多源输入过程中的干扰源定位

当电压波形和电流波形发生畸变时，我们不能仅仅通过这两个信号的波形的畸变程度去判断某个输入源就是影响电能质量的根源，比如对于研究背景谐波作用于线性负载多输入源时，如果该系统并网时电压和电流的波形发生了畸变，我们不能认为是多输入源造成的，因为多输入源在并网中如果都是线性的，电压和电流信号是不会发生畸变的，这时候电压和电流波形发生畸变的主要原因是非线性负载造成的，不是多输入源造成的。

这里我们要看到(r、1)是负载的阻抗参数，本文通过监测负载阻抗参数的变化去计算出负载非线性的程度，然后通过检测多输入源系统在并网过程中系统波形发生的畸变程度，可以判断出在负载阻抗参数变化比较大的多输入源系统具有很强的非线性，对电网波形畸变会产生更大的影响。我们假设负荷静态电感、负荷静态电阻、负荷电流、负荷电压分别用l(t)、r(t)、i(t)、u(t)来表示的微分方程如下所示：

(1)

假设输入源系统的负载参数是不变的，电压和电流的关系如式(2)所示：

(2)

电压和电流的关系还可以用相量的形式来表示如式(3)所示：

(3)

微分方程式(2)是描述当系统处在稳定状态是负载静态阻抗、负载静态电感发与负载电压和电流的关系，这里大家要注意负载电流中的谐波频率也许和电压当中不同，而式(3)前提条件是电压和电流的谐波的频率是相同的，其中的h表示谐波的次数，负载自身是不会产生其他频率的谐波分量的，如果负载电流中其他频率的谐波分量必然是由负载电压造成的。下面举例说明，假设电流表达式为i(t)=1.414×sin(100t)，也就是说静态电阻用r(t)=1+0.05cos(500t)、静态电感用1(t)=0.001+0.00005×sin(300t)表达式表示，其具体波形如图1和图2，我们能从电压波形中得出其中有2、4、6次谐波频率成分。

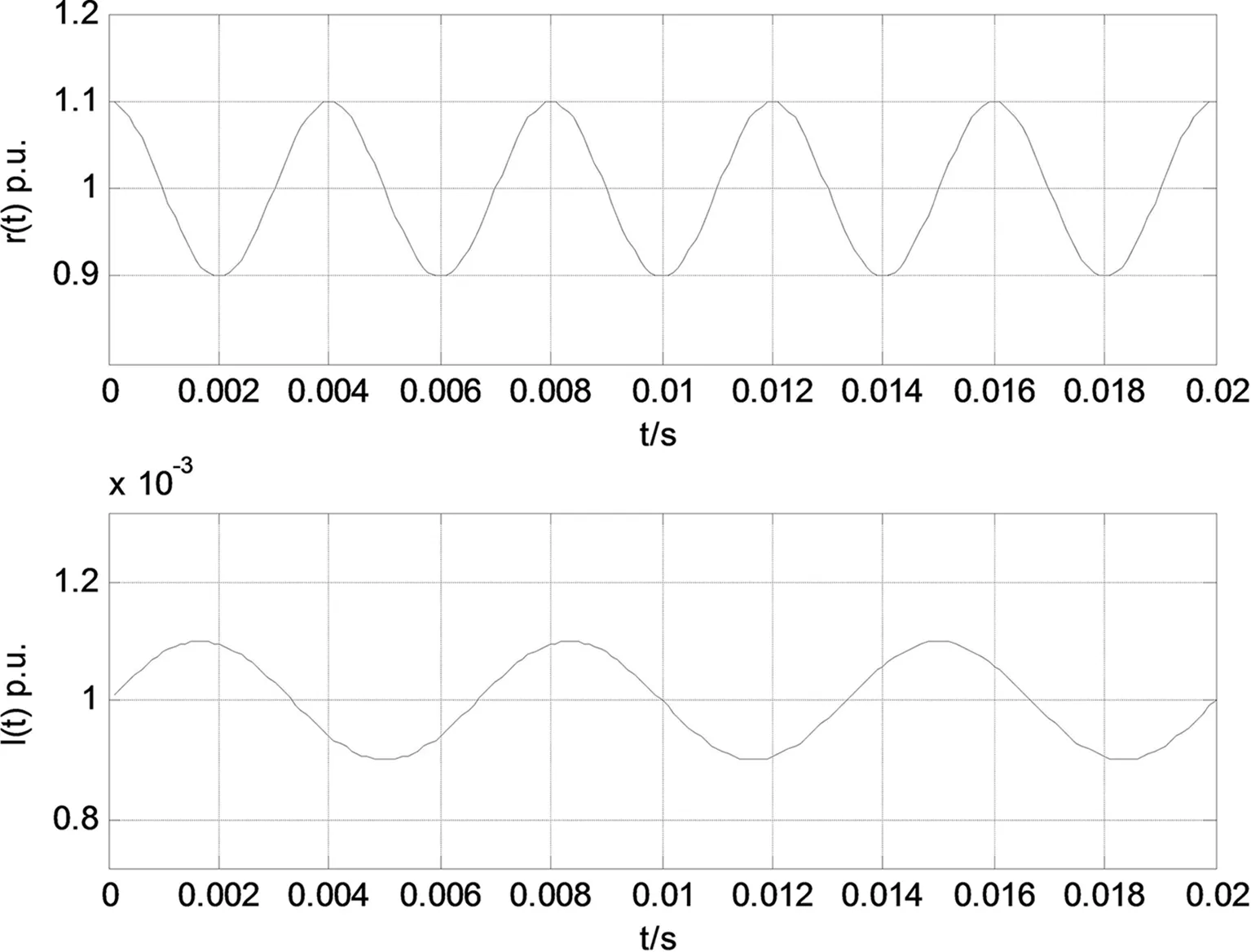
图1 静态阻抗变化曲线

图2 负荷电压频谱分析

通过第一种定义的方法我们用来衡量当多输入源系统中某个负载参数发生变化的程度，其非线性程度，当我们监测的时间取值较长的时候，根据第一种定义的方法可以将分段恒定的多输入源头中的某个负载误认为是非线性输入源，为了改善这个误判断我们进行了优化，具体如式(2)和式(3)所示。

(4)

(5)

1.3 多输入源中某个输入负荷污染的度量

前面我们通过从多输入源中对某个输入负载参数的变化去衡量它的非线性程度，该方法不能直接确定当非线性多输入系统中的负载接入到公共点之后，此时对电能质量影响程度，我们需要能直接衡量其对电能质量的影响程度。在实际应用中，我们通过公共连接点电压UPCC的指标变化来衡量多输入信号和非线性负载之间的相互影响，所以我们可以通过比较多输入源中接入某个负载接入公共连接点电压的前后变化可以直接衡量电能指标的变化，也可以衡量其对电能质量的影响程度。具体如图3所示。

图3 系统中某个负荷接入图

如果us、rs、ls关系已知，非线性多输入源中某个负荷的参数rnl、lnl的关系有以下微分方程，则可计算出电流I和电压UPCC。如式(6)所示。

(6)

设Fs是采样频率，将上式离散化可以得到式(7)。

us(k)=[rs+rnl(k)]·i(k)+[ls+lnl(k)]·[i(k+1)-i(k)]·Fs

upcc(k)=us(k)-rs·i(k)-ls·[i(k+1)-i(k)]·Fs

(7)

这时我们可以求解出零状态输出u0pcc(t)，如果我们用较长的时间来计算输出，则过渡过程项不用计算，然后得到该系统的稳态输出upcc(t)。得到稳态输出和零状态输出值就可以计算公共连接点电压的总谐波畸变率了。

THD-upcc来表示，而NLFH=THD_upcc是用来表示非线性多输入源中某个负荷对电力系统的波形发生畸变程度性能指标。Pst upcc来表示公共连接点电压的短时间内的闪变值，NLFP=Pst_upcc用来表示本文研究系统中某个负载对电力系统电能波动影响性能指标。如果系统有谐波干扰信号，我们就下输入电压中随机加载感染信号进行模拟系统的真实的干扰信号，upcc这个指标来衡量系统接入某个负载的前后变化，再来定义可定义NLFH=THD upcc,NLFP=Pst upcc。我们也可以用另外一种方法来测评该系统的某个负载的非线性程度，我们比较某个负载电压NLFH和NLFP即可。

1.4 举例验证

比如10kHz为系统采样信号的频率，通过人为设置参数去模拟系统总负载性能指标，这样再计算，这样做的原因是为了更准确地去贴近实际中真实的系统。下面我们来对NLFH进行计算，如果该系统中某个负载是纯电阻，则该电阻的标幺值会在1附近呈矩形振荡，其振荡频率为150Hz，该标幺值的振幅dr从0.1递增到1.5时，纯电阻的变化图形如图4所示，随着电阻振幅逐渐增加，其对应的NLFH变化规律如图5所示。其中是该系统某个负载电阻变化振幅递增时，它的变化和该系统的某个负载特性变化是相同的。

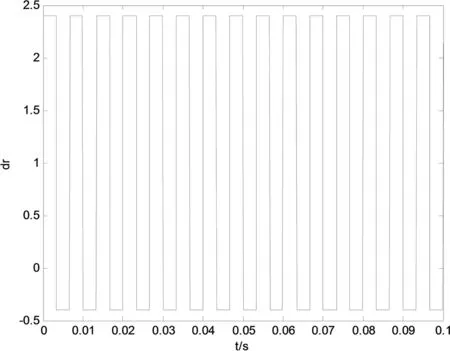
图4 频率150Hz振幅1.5的电阻变化

图5 NLFH对应电阻振幅增加的变化

计算完NLFH后我们在对NLFP进行分析计算，我们依然假设该系统的某个负载是纯电阻特性，电阻的标幺值还是在1附近呈现矩形振荡，其频率是8.8Hz，其振幅的变化是从10-4递增到1.5×10-4，可以得出当该系统某个负载变化幅度增加是NLFP也逐步递增，和上面的变化是相同的。

通过以上分析我们可以得出，构建的松散式多源输电光伏并网发输入稳定性监测系统，对已有的光伏发输入电网并网的稳定性进行了算法仿真分析，验证了为本文设计的正确性，通过本文构建的系统可以有效监控松散多源输电并网的稳定性，提高多源输电光伏并网发电系统的稳定性分析及干扰源定位分析效率。