基于WPT和BP神经网络的转辙机故障诊断方法研究

郭文玥,冯庆胜

(大连交通大学 自动化与电气工程学院，辽宁 大连 116028)

转辙机作为改变道岔开通方向的动力设备，对保障列车安全运行具有重要的作用.由于转辙机的工作环境大部分处于室外，昼夜温差和恶劣天气都可能影响转辙机的正常工作.目前转辙机主要利用微机监测系统采集的电流或功率信号设定阈值来判断是否发生故障，该方法灵活性低、漏判率高.于是加入人工筛查进行二次判断，导致实时性差、效率低，不能形成系统的、智能的维护维修规划.

目前，国内外学者对转辙机故障诊断进行了一定程度的研究，采用的方法也是各有特色.Zhou等[1]虽然根据专家的经验知识得到了部分特征，但无法对主成分分析过程进行控制，可能提取不到有效特征.李嘉鹏等[2]采用小波-包络解调方法提取特征，虽然实现了复合特征的分离提取，但缺乏信号的高频信息.Atamurada等[3]采用专家系统进行故障诊断，设定规则较少，对一些相似信号无法区分.张旭等[4]利用小波分析和主成分分析法进行特征提取和数据降维，该方法需经两步提取特征，烦琐耗时.Long等[5]采用哈尔小波提取特征缺乏低频细节信息.还有通过计算转辙机电流信号平均值、方差、最大值等相关数值作为特征值，并结合隐马尔科夫模型[6]、支持向量机[7]、灰色神经网络[8]等进行故障诊断，这些方法提取的特征缺乏细节信息，且识别率都低于98.5%.王晓煜等[9]采用BP神经网络进行铝板结构损伤识别，可以实现对缺陷尺寸的精确定量，且具有较高的稳定性.董昱等[10]验证了小波包提取故障的有效性，但无法直接进行故障识别.

本文利用小波包变换对转辙机动作电流信号进行分解重构，得到不同频率段的能量值，然后将能量值归一化处理组成特征向量集，输入经参数调优的BP神经网络模型，实现转辙机状态的智能诊断.

1 转辙机动作曲线分析

1.1 动作曲线与转辙机故障间的关系

转辙机动作曲线一般指转辙机的工作电流曲线，它的曲线特征代表了转辙机的各个组成部件的动作状态、电气和机械特性.曲线各个阶段的异常变化代表着转辙机动作过程中参与部件可能发生的故障.通过对某个转辙机动作电流曲线的查询与分析,可以判断该转辙机的工作状态，及时发现和消除隐患，对列车安全运行有着重要的意义.

1.2 转辙机正常动作时的电流曲线分析

本文以ZD6型转辙机为研究对象，在其正常转换过程中的工作电流曲线，见图1.

图1 转辙机正常动作的电流曲线图

ZD6型转辙机的动作过程主要分为四个阶段:

解锁阶段(T1-T4)：解锁时间小于等于0.6 s，电动机启动，通过主轴旋转带动锁闭装置进行解锁.T1点1DQJ吸起，转辙机动作曲线开始记录；T2-T3，2DQJ转极，动作电流曲线骤升形成一个尖峰，峰顶值通常为3～7A；T3-T4，电流至峰点后迅速回落到一定值后趋于平滑.

转换阶段(T4-T7)：道岔成功解锁后，锁闭齿轮和齿条块动作，带动尖轨位移至规定位置.该阶段电流曲线较为平滑，其转换时间长短由阻力大小决定.

锁闭阶段(T7-T9)：锁闭时间小于等于0.3 s，尖轨到位后与基本轨密贴，自动开闭器接点自动断开电动机动作电路，电动机惯性在摩擦带的消耗下，其动作电流曲线逐渐下滑，最后降为零.

缓放阶段(T9-T10)：缓放时间大于等于0.4 s，道岔锁闭后，会形成一段近似为零的曲线.T10点1DQJ落下，转辙机动作曲线记录结束.

1.3 转辙机故障工作时的动作电流曲线分析

根据查阅资料和现场调研，目前ZD6型转辙机主要有8种常见故障[11]，故障详情如表1所示，对应的电流曲线见图2.

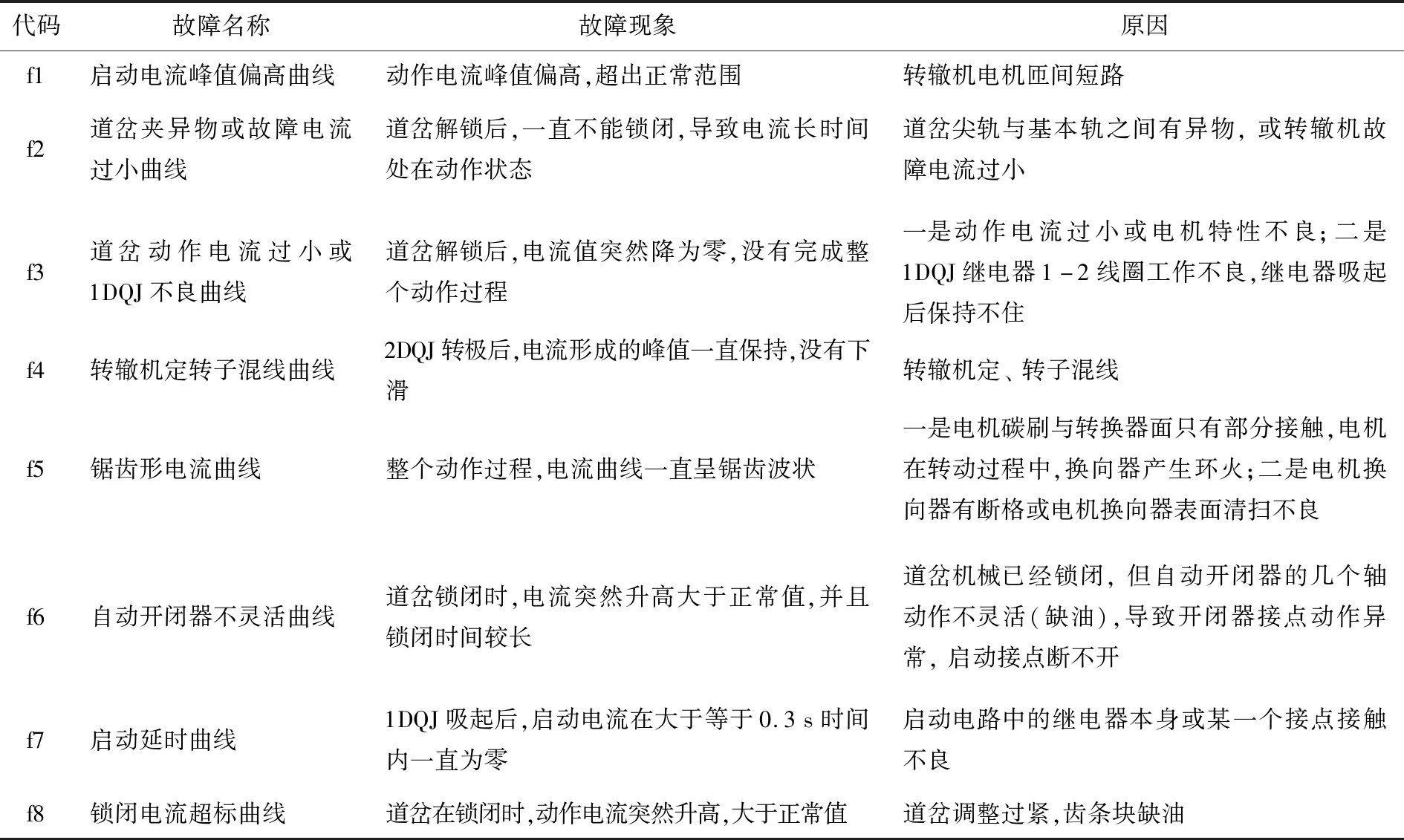
表1 ZD6型转辙机常见故障分析

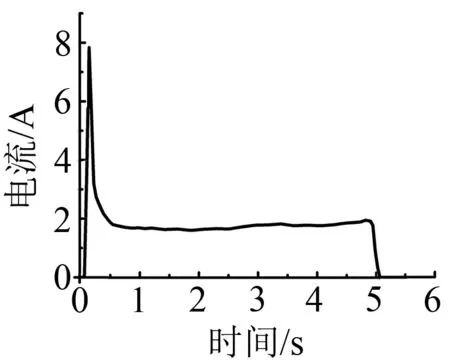
(a) f1启动电流峰值偏高

(e) f5 锯齿形电流

2 动作电流曲线的小波包处理

2.1 小波包变换

小波包变换(Wavelet Packet Transform，WPT)是对信号进行更精细、无冗余、无疏漏的一种分析方法，它分解的高低频信号能在更加细化的频带内进行.小波包定义如下，假设信号为y(t),则

(1)

式中：函数系{yn(t)}称作正交小波包;h(k)为低通滤波器;g(k)为高通滤波器;h(k)和g(k)两者之间互为正交关系.

2.2 动作电流曲线特征提取

小波包分解的过程可以看作对信号进行滤波，每层分解由一组高通滤波器和一组低通滤波器实现，在对信号进行处理时，每次分解产生的所有信号均参与下一层的分解，使得转辙机动作曲线每一个频段的信号都能得到全面的表征，提取的特征能更好地反映转辙机的动作过程.具体步骤如下：

(1)对原始信号进行N层小波包分解，得到2N个不同频带的分解系数，对得到的所有高低频分解系数进行小波包重构，重构系数表示为SN,k(k=0,1,…,2N-1)，计算每个频带的小波包能量值：

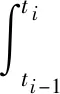
(2)

式中:ti-1-ti是该频带信号的起止时间.

(2)考虑到信号的部分频段的能量可能会过大，因此将对每个频带的能量进行归一化处理，得到归一化值pN,k：

(3)

将现场采集到的原始动作电流信号进行三层小波包分解，通过MATLAB分解、重构，得到各频段信号能量值，组成信号故障特征向量，即

(4)

正常状态(用f0表示)和8种常见故障状态信号小波包分解重构得到的故障能量值见表2.可以看出，当转辙机发生故障时，某些频带的能量值(如f3、f4、f7)与正常状态频带的能量值(f0)相差很大，但是有些不同的类型(如f0、f1、f5等)，其频带能量值的分布很相似，无法直接看出转辙机的具体故障，因此选用BP神经网络模型进行故障分类.

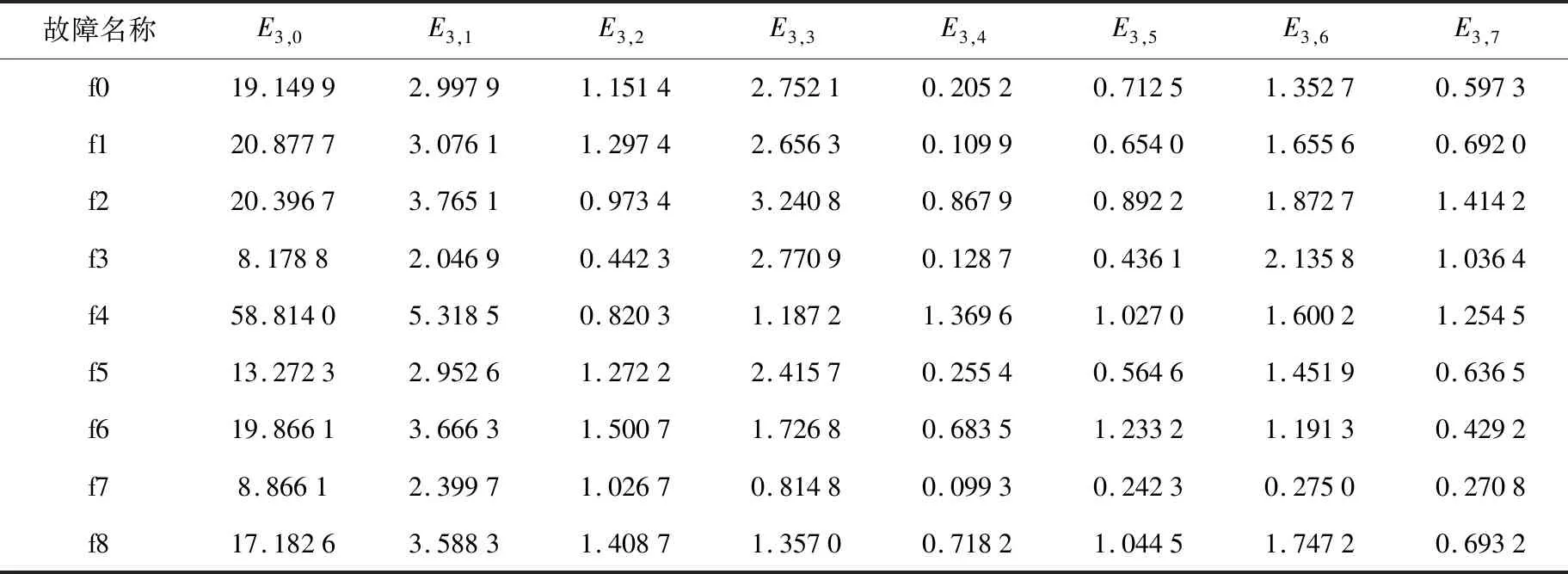
表2 正常状态与故障状态小波包分解能量值

利用MATLAB归一化函数mapminmax对故障特征向量处理得到BP神经网络的输入.

3 故障诊断

3.1 故障诊断系统流程

转辙机故障诊断系统主要由电流特征提取和故障诊断两部分组成，故障诊断系统结构图见图3.

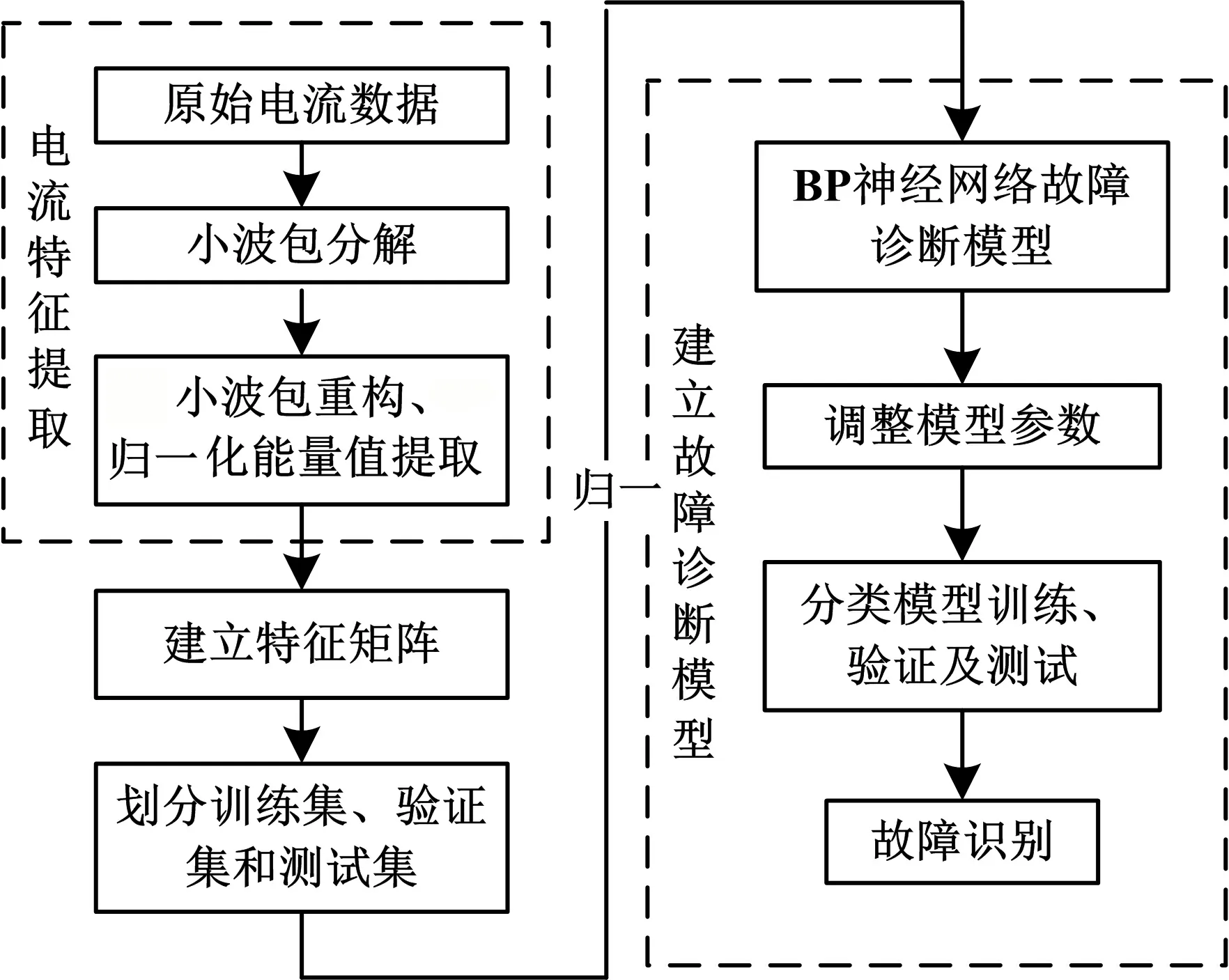
图3 故障诊断系统结构图

3.2 BP神经网络的构建

构建三层BP神经网络模型，设计输入层为归一化得到的故障特征集的个数为8个神经元；输出层为不同故障类型目标输出为9个神经元；隐含层神经元个数的确定参考如式(5)[3]：

(5)

式中:m,n分别为输入、输出层神经元个数；a为0～10之间的常数.

对BP神经网络的各层函数进行调整寻优，最终确定输入层和隐含层传递函数采用tansig函数，隐含层和输出层采用purelin函数，神经网络参数训练采用trainlm函数.

4 仿真及结果分析

利用铁路现场采集到的ZD6型转辙机动作电流数据进行实验，其动作一次时间为5 s，系统每隔0.04 s采集一次数据，采集点125个.选择样本数据3 600组，其中2 160组为训练样本，720组为验证样本，720组为测试样本，各类型样本数量见表3.

表3 模型训练及测试数据集表

采用db3小波基对原始样本数据进行分解，得到第三层8个小波包系数重构信号，见图4.可以看出，S3,0小波系数的幅值最大，与表2中E3,0能量值最高相一致.

图4 小波包变换重构信号

根据构建的神经网络，设定训练迭代次数为2 000次，训练目标最小误差为1×10-5，学习速率为0.01.经训练、验证和测试，为隐含层神经元为9时，模型的均方误差最小.采用不同模型参数和不同特征提取方法的训练迭代次数和均方误差曲线见图5.若采用文献[1]tansig+tansig+traingdx函数训练(图5(a))，BP神经网络训练迭代次数为150步，此时诊断的准确率为95.9%；采用PCA-WT提取特征(图5(b))，迭代次数为105步，诊断准确率为98.0%.若采用文献[3]tansig+logsig+trainlm函数训练(图5(c))，迭代次数为270步，此时诊断的准确率为83.8%；采用HAAR小波提取特征(图5(d))，迭代次数为97步，诊断准确率为98.3%.若采用文献[4]在时域上的道岔转换状态提取特征(图5(e))，迭代步数为129步，诊断准确率为97.8%.本文选用小波包提取特征和寻优后tansig+purelin+trainlm函数(图5(f))，迭代次数为79步，此时诊断的准确率为99.3%.由于测试集数据多，分类结果过于集中，故选择其中部分数据的分类结果进行展示，见图6.

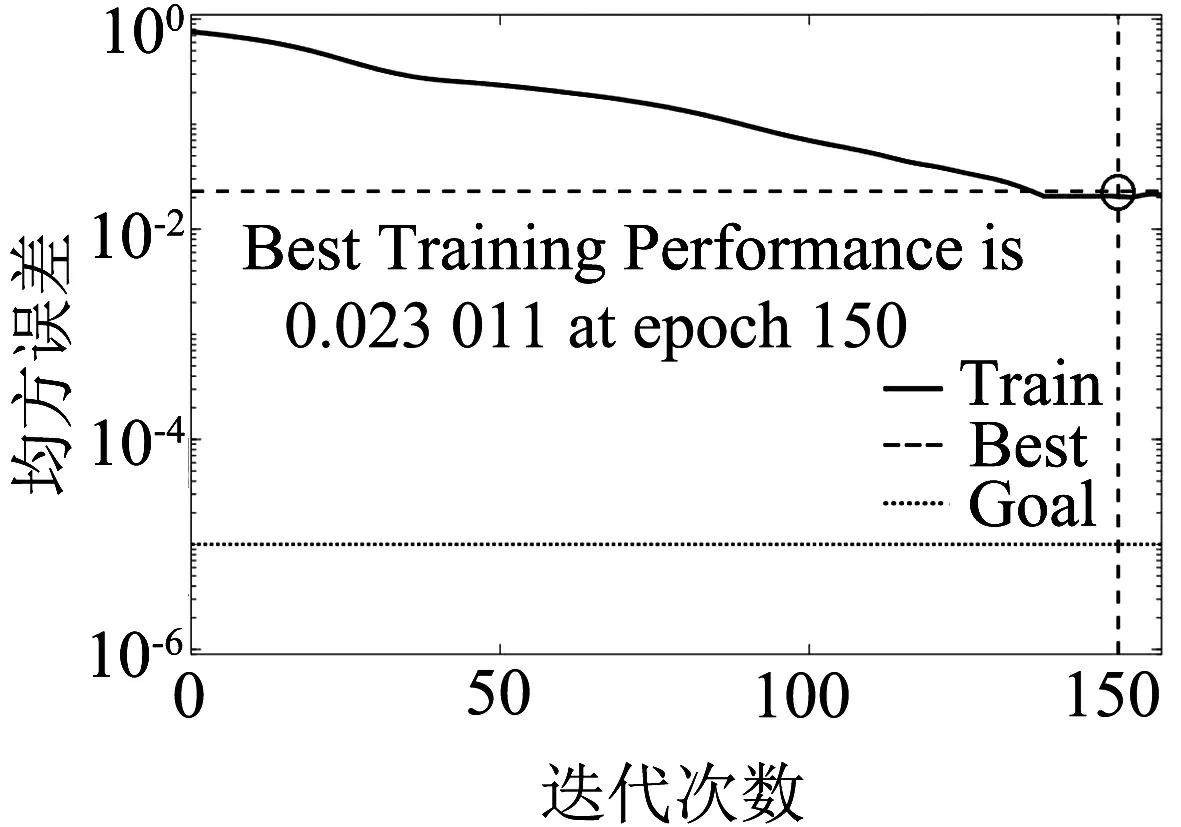
(a)tansig+tansig+traingdx

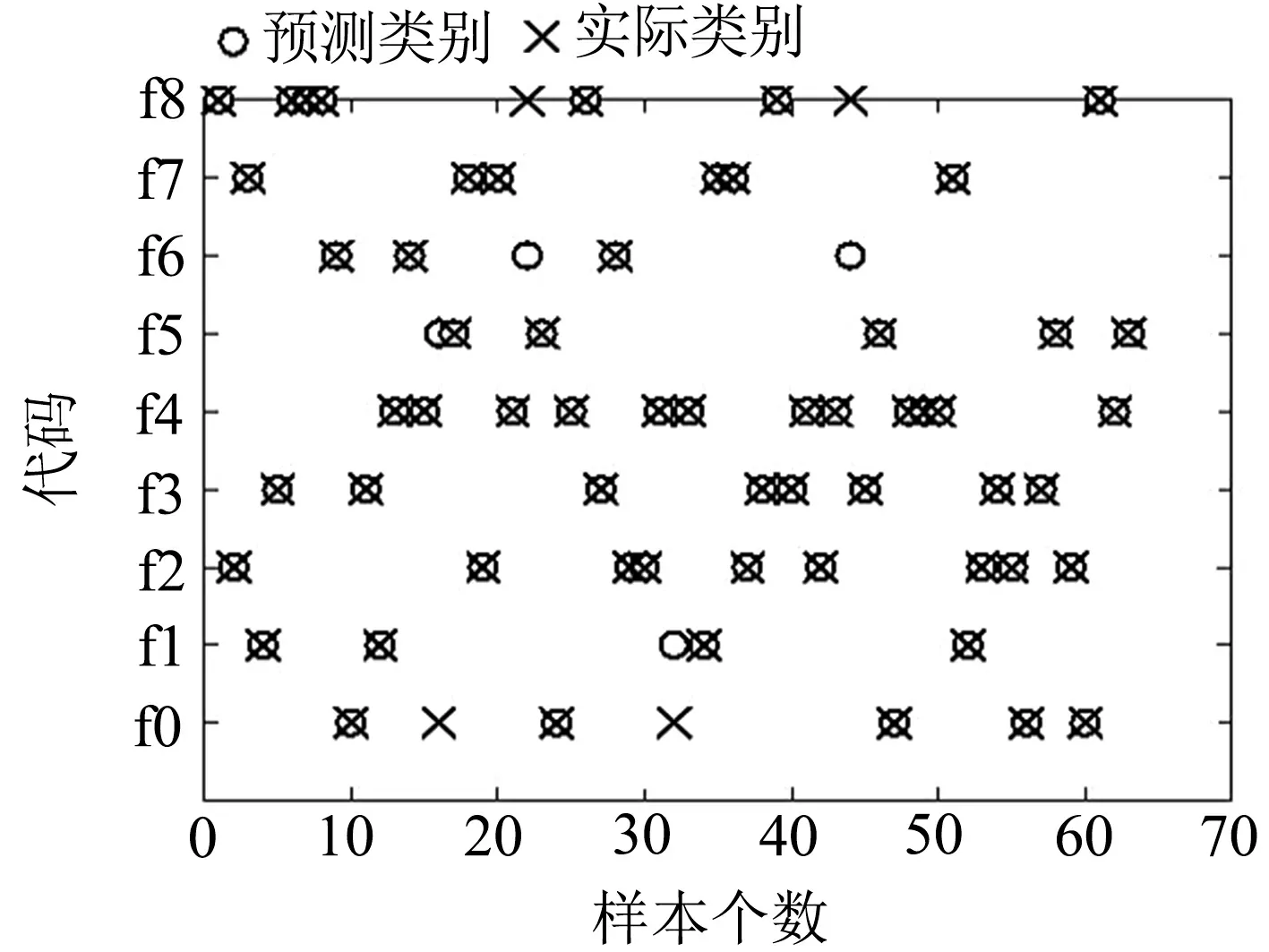
图6 预测集样本部分数据分类结果

分类结果中，f1(启动峰值偏高)、f5(锯齿形电流)被识别为f0(正常电流)，f6(自动开闭器不灵活)被识别为f8(锁闭电流超标)，通过能量值分布可以看出，这几种分布结果很接近，导致模型识别错误.

采用不同函数参数BP神经网络的测试结果见表4，采用其他特征提取方法的测试结果对比见表5，可以看出本文采用小波包进行故障特征提取和经过调整寻优后的BP神经网络相结合的方法，迭代次数最低、故障诊断准确率最高，能够满足铁路现场故障诊断的需求.

表4 不同神经网络函数结果对比

表5 不同特征提取方法的结果对比

5 结论

本文利用小波包变换提取转辙机动作电流特征值，该方法得到了信号的时频域联合分布信息，即不同时间和频率的能量值分布，相比直接提取时域特定参数值更能反映原始信号的突变信息，将得到的特征向量经寻优调整后的BP神经网络模型诊断后，准确率达到了99.3%，能够满足铁路现场维护的需求.由于ZD6型转辙机动作曲线与ZDJ9、S700K等转辙机动作曲线具有一定的相似性，因此本文研究方法亦适用于这些类型的转辙机故障诊断.