高速列车头型的减阻降噪多目标优化设计
2022-12-14季玲刘海东陈秉智
季玲,刘海东,陈秉智
(大连交通大学 机车车辆工程学院,辽宁 大连 116028)
随着列车运行速度的提高,空气阻力、空气升力和空气噪声等空气动力学问题的影响逐渐加剧[1-2].当列车速度达到300 km/h时,空气阻力占总阻力的75%,增加了列车能耗;空气升力降低了列车运行的安全性,正升力过大,轮轨间作用力严重降低时甚至导致列车脱轨;负升力过大,轮轨间磨耗增加;空气噪声成为主要噪声源,降低了乘坐舒适性[3-8].列车空气阻力、空气升力和列车表面噪声源声功率与头型几何曲面有密切关系,故列车头型的优化设计成为改善高速列车的噪声性能和气动性能的主要措施[9-10].Sun等[11]和姚拴宝等[12]以空气阻力为目标,分别采用MOGA-Ⅱ和改进的蚁群算法对列车头型进行优化设计.李明等[13]以空气阻力和空气升力为目标,分别采用伴随方法和NSGA-Ⅱ算法,对列车头型进行多目标优化.Krajnovic[14]以横风稳定性和空气阻力为目标,研究3种近似模型对列车优化设计的影响,结果表明:径向基神经网络和多项式函数的组合模型效果较好.刘加利等[15]对列车头型进行多目标优化设计,降低列车的空气阻力和偶极子噪声源.于梦阁等[16]以空气阻力和轮重减载率为目标,基于Kriging近似模型对列车头型进行多目标优化,优化后列车的空气阻力减小3.27%,轮重减载率减小1.44%.
以上研究工作专注于优化高速列车头型的气动性能,较少同时考虑列车的噪声性能和气动性能,并且大多数气动头型优化研究仅仅针对一个或两个气动优化目标进行研究,得到的优化头型效果有限.此外,对高速列车头型进行优化设计时,每次优化迭代都需要对整车模型进行参数化几何建模、网格划分和空气动力学计算,优化设计时间长.因此,本文采用Isight软件集成Sculptor和Fluent模块,以高速列车的空气阻力、空气升力和列车表面噪声源声功率为优化目标,运用ASD技术和响应面近似模型,采用NSGA-Ⅱ算法对高速列车头型进行多目标自动优化设计.
1 优化设计流程
本文设计了如下的优化流程(图1),运用ASD技术快速建立列车网格模型,经空气动力学计算得到优化目标值,构建设计变量关于优化目标的响应面近似模型,并采用NSGA-Ⅱ算法进行多目标优化设计.
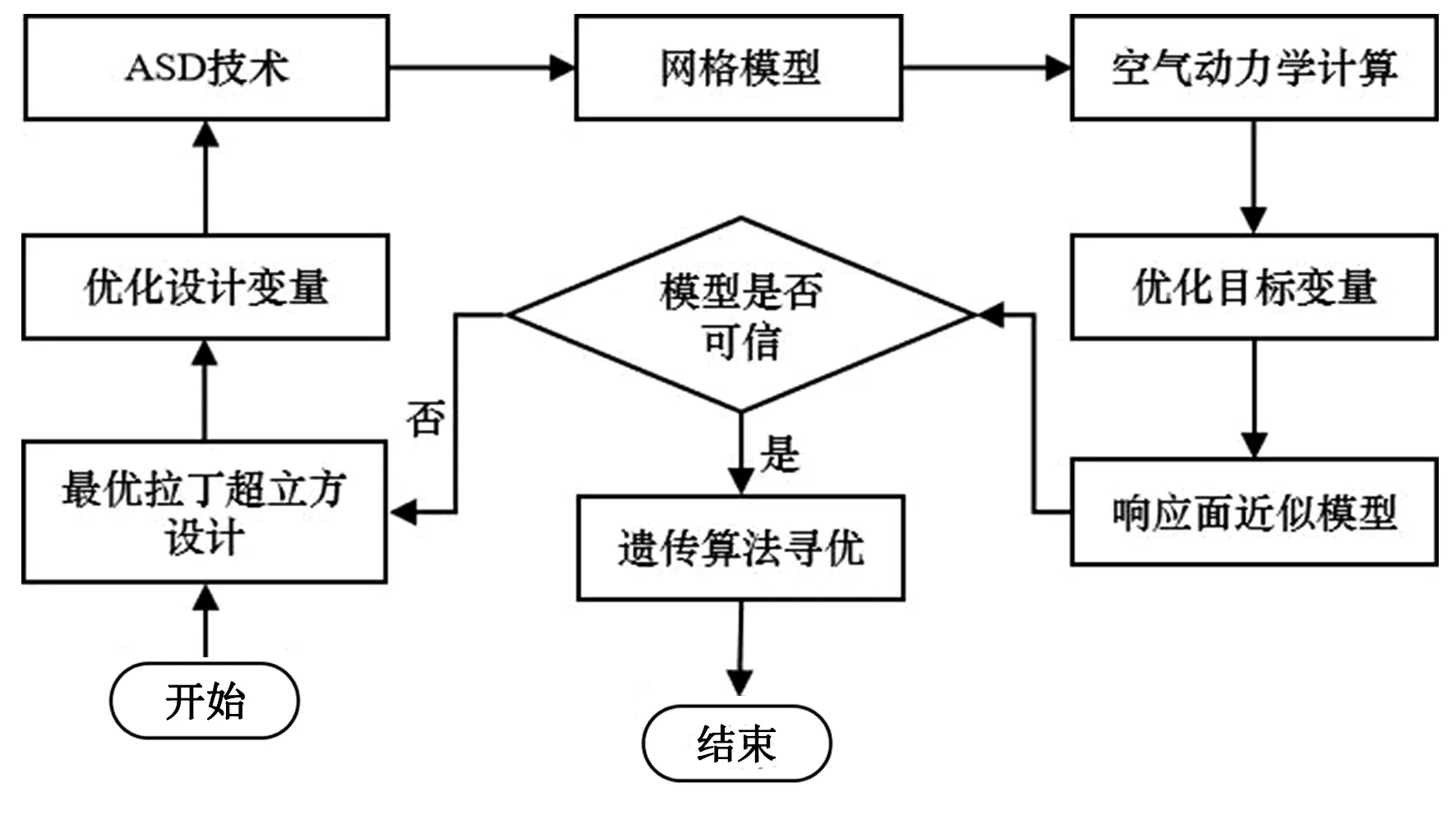
图1 优化设计流程
2 高速列车空气动力学模型
2.1 控制方程
本文高速列车运行时马赫数小于0.3,可以忽略空气密度变化对流场的影响[17].因此,采用三维不可压缩非定常方程进行模拟:
连续方程:
(1)
N-S方程:
(2)
式中:ui、uj为流场速度;xi、xj为坐标分量;ρ为空气密度;p为热力学压强;μ为空气动力黏度.
高速列车周围流场采用k-ε模型模拟.
湍流黏性系数μt为:
(3)
湍流动能k方程为:
(4)
湍流耗散率ε方程为:
(5)
式(3)~式(5)中:Cu为湍流常数,取值为0.09;c1、c2、σk、σε为经验常数,取值分别为1.47、192、1.0、1.33.
Proudman方程利用Lighthill理论模拟各向同性湍流运动声功率:
(6)
式中:α为模型常量;ρ为空气密度;u为湍流速度;l为湍流尺度;c0为声速.
声功率级Lp为:
LP=10 lg(PA/Pr)
(7)
式中:Pr为参考声功率;Pr=10-12W/m3.
声功率可以估计单位体积或面积的局部噪声.
2.2 数值模型
本文计算模型为三节编组列车(头车+中间车+尾车),列车运行速度为350 km/h.对高速列车车头表面网格细化,最大尺寸为50 mm,其他部位网格不超过100 mm.流场采用四面体网格离散,网格最大尺寸为2 400 mm.流场左侧为速度入口边界,右侧为压力出口边界.地面为运动壁面,移动速度与入口速度相同,模拟地面效应.在高速列车稳态计算的基础上,利用宽频噪声模块计算列车表面噪声源分布.模型计算区域见图2,列车流线型头型网格模型见图3.
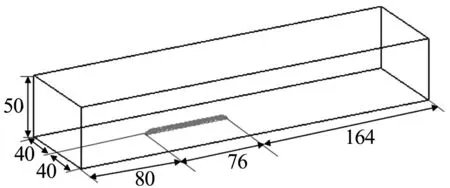
图2 模型计算区域

(a) 列车头型网格
3 网格驱动变形技术
3.1 ASD技术
本文采用基于Sculptor软件的网格驱动变形技术(Arbitrary Shape Deformation,ASD)在网格处建立控制体,一个ASD控制体包括多个控制点及控制点间连线.控制点移动,相邻区域网格随之移动,实现网格变形.网格移动满足C1连续,保证网格光滑变形.网格驱动变形技术为复杂模型的外形优化供了可行性.
3.2 定义设计变量
选取高速列车模型的控制点,控制列车车头形状.在车头顶部选取5个设计变量(dy1、dy2、dy3、dy4和dy5),控制车头沿垂向变形;在车头两侧选取设计变量dz,控制车头沿横向变形;在车头前部选取设计变量dx,控制车头沿纵向变形.高速列车头车和尾车控制点对称布置图,控制点布置见图4.根据工程经验,设计变量的取值范围见表1.

(b) 流场纵向对称面网格图4 控制点布置

表1 设计变量取值范围
4 多目标优化计算及结果分析
4.1 多目标问题描述
本文以高速列车的空气阻力绝对值最小化、空气升力绝对值最小化和列车表面噪声源声功率最小化为优化目标,进行多目标优化设计.
4.2 构造响应面近似模型
采用最优拉丁超立方采样法选取200组样本,分别构建列车空气阻力、空气升力和列车表面噪声源声功率的四次多项式响应面近似模型.随机选取10个样本点进行误差分析,检验近似模型精度,分析指标包括:均值(Average)、最大值(Maximum)、均方根(Root Mean Square)、相关系数(R-Squared).列车空气阻力、空气升力和列车表面噪声源声功率的预测值与真实值对比见图5.列车空气阻力、空气升力和列车表面噪声源声功率的预测值与真实值基本接近.表2给出了近似模型的误差分析结果,列车空气阻力、空气升力和列车表面噪声源声功率的误差均满足相应的误差分析指标要求.

(a) 空气阻力对比

表2 近似模型误差分析
4.3 优化结果分析
本文基于列车空气阻力、空气升力和列车表面噪声源声功率的四次多项式响应面近似模型,采用第二代非劣排序遗传算法NSGA-Ⅱ对高速列车头型进行多目标优化设计.NSGA-Ⅱ算法的种群规模设为24,进化代数为24代,交叉概率为0.9.将多个目标函数合并为单目标时,需指定各目标函数的缩放因子和权重系数.本文的三个优化目标数量级相差较大,为得到均衡的优化结果,目标函数的缩放因子和权重系数见表3.

表3 缩放因子和权重系数
优化目标的Pareto前沿解集见图6.表4给出了从Pareto前沿解集中选取的新头型P1~P5和优化前原头型P0的气动性能和噪声性能对比.新头型P1为空气阻力最小的头型;新头型P2为空气升力最小的头型,同时新头型P2为Pareto最优解;新头型P5为列车表面噪声源声功率最小的头型.选取最优新头型时,应确保新头型的空气阻力、空气升力和列车表面噪声源声功率都小于原列车的初始值,故不考虑新头型P5.因为新头型P1~P4的空气阻力和列车表面噪声源声功率变化比例较小,选择空气升力最小的新头型P2作为优化后的模型进行分析.优化后,列车空气阻力减小5.20%,空气升力减小36.68%,列车表面噪声源声功率减小2.11%,列车的气动性能和噪声性能有所改善.
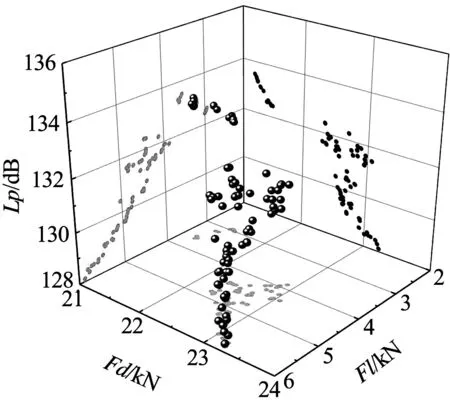
图6 优化目标的Pareto前沿解集

表4 优化前后模型的结果对比
对优化后的列车头型进行空气动力学计算验证,结果见表5.列车空气阻力的相对误差为0.06%,空气升力的相对误差为2.26%,列车表面噪声源声功率级的相对误差为0.54%,优化结果与空气动力学仿真计算结果的误差在允许范围.

表5 优化结果验证
表6给出了当高速列车速度为300 km/h、400 km/h和500 km/h时优化前、后的列车气动性能和噪声性能对比.相比于原头型,优化后的列车头型在不同速度下的空气阻力、空气升力和列车表面噪声源声功率都减小,列车的气动性能和噪声性能提高,有较好的优化效果.随着列车速度提高,列车的空气阻力和空气升力的变化比例增大,列车表面噪声源声功率的变化比例减小.
图7给出了优化前、后列车头型的变量变化幅值.图8给出了优化前、后列车的流线型头型对比,虚线为优化前的原头型,实线为优化后的列车头型.与原头型相比,优化后头型的鼻锥前伸量增大,鼻锥宽度减小,鼻锥高度增高,观察窗高度增高且内凹,车头与车身过渡处高度降低.

表6 不同速度下优化前后模型的结果对比
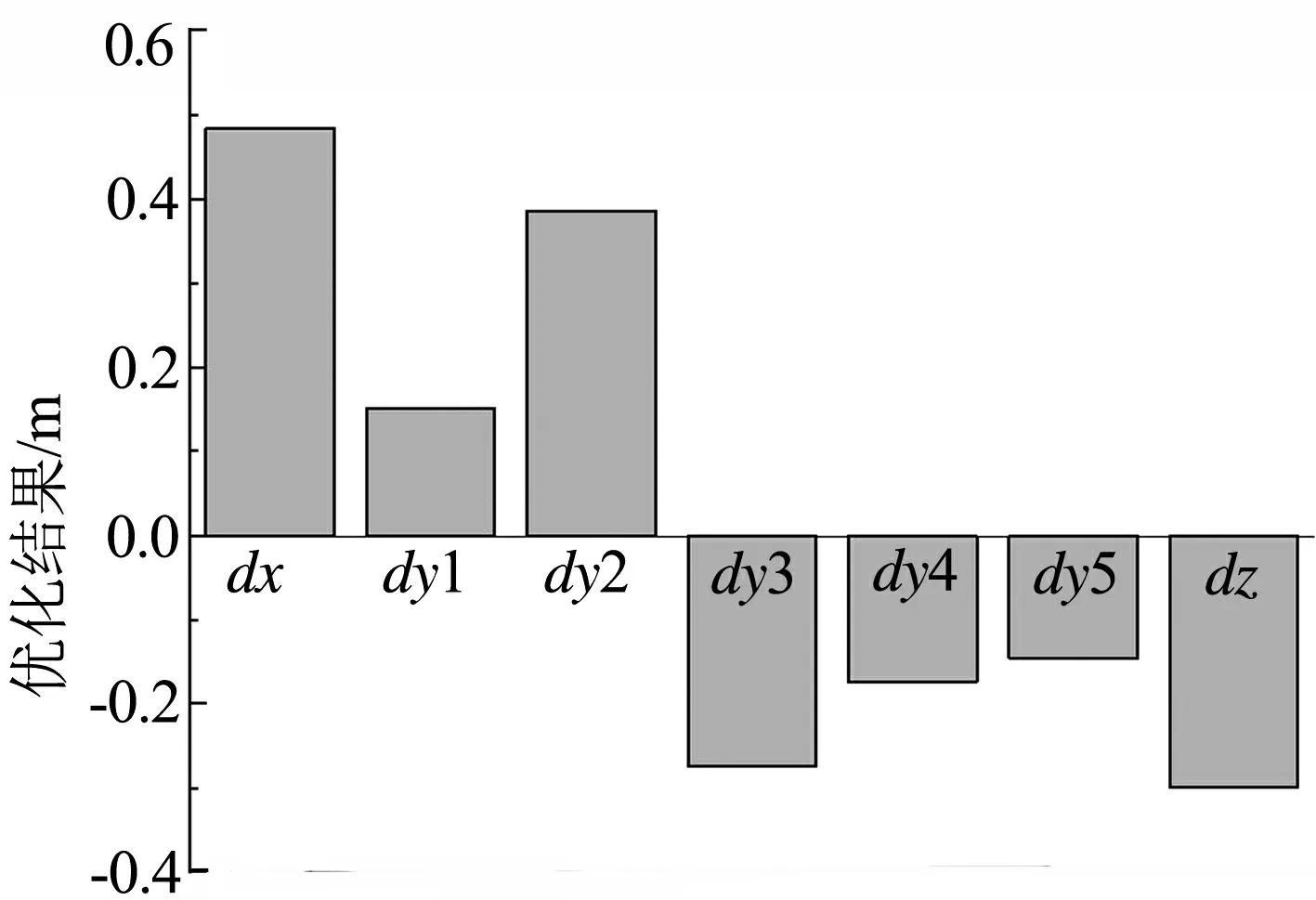
图7 变量变化幅值

(a) 垂向视图
图9给出了优化前、后列车头型表面的压力分布,优化后高速列车头车的正压区比优化前原头型头车的正压区小,正阻力减小;尾车的正压区比原头型尾车的正压区大,负阻力增大,故优化后列车的空气阻力降低.优化后尾车鼻锥顶部正压区比原头型尾车的正压区大,故优化后列车的空气升力降低.优化后列车头车的正压区比原头型头车的正压区分布更均匀,气流扰动程度降低,故优化后列车表面噪声源声功率降低.

(a) 头车表面压力分布图9 优化前、后列车头型表面压力分布
5 结论
(1)本文以高速列车空气阻力、空气升力和列车表面噪声源声功率为优化目标,运用ASD技术和响应面近似模型,采用遗传算法NSGA-Ⅱ,对高速列车头型进行多目标自动优化设计,缩短高速列车流线型头型的优化时间,提高优化设计效率.
(2)相比于原头型,优化后的高速列车头型鼻锥前伸量增大,鼻锥宽度减小,鼻锥高度略增高,观察窗高度增高且内凹,车头与车身过渡处高度降低;优化后的列车空气阻力减小5.20%,空气升力值减小36.68%,列车表面噪声源声功率减小2.11%,列车的气动性能和噪声性能提高,且在不同运行速度下,都得到较好优化效果,具有一定工程参考价值.
