凹底平车车辆大小底架强度及模态分析

许钦华，徐聪，李家宝

(中车青岛四方车辆研究所有限公司，山东 青岛 266031)

凹底平车作为铁路常见的特种车辆，主要用于运输长大类特种货物，这类车辆一般自重大、尺寸长、结构复杂、制造周期较长，一般需要结合有限元对车体结构的强度、刚度进行计算，识别相应的模态频率，为后期设计提供参考.近年来，关于铁路货车的标准更新较快，对凹底平车等长大货物车强度相关研究的文章较少，未对具体的加载及约束进行介绍，也未对计算工况的设置依据进行阐述.

本文研究了凹底平车强度分析的工况及评估依据、有限元模型加载及约束方式、部分结构的优化及改进方法、不同模型边界约束方式对大底架结构振型频率的影响等，为同类车型的强度及模态等相关研究提供借鉴.

1 车辆结构

凹底平车车辆为双层底架结构，主要由一个大底架、两个小底架、四个转向架、制动装置及车钩缓冲装置等组成.大底架与小底架之间、小底架与转向架之间均通过心盘结构连接[1].

大底架为焊接结构，主要由中部上盖板、两层中部下盖板、端部上盖板、端部下盖板、弯角上盖板、弯角下盖板、四层纵向腹板、若干隔板、若干筋板、若干外檐板等组焊而成，材料为Q345E高强度耐候钢，具体结构(局部)见图1(a).小底架为焊接结构，主要由中梁、枕梁、牵引梁、纵向腹板等组成，中梁下盖板和牵引梁下盖板的材料为Q460E高强度耐候钢，其他材料为Q345E高强度耐候钢，具体结构(局部)见图1(b).

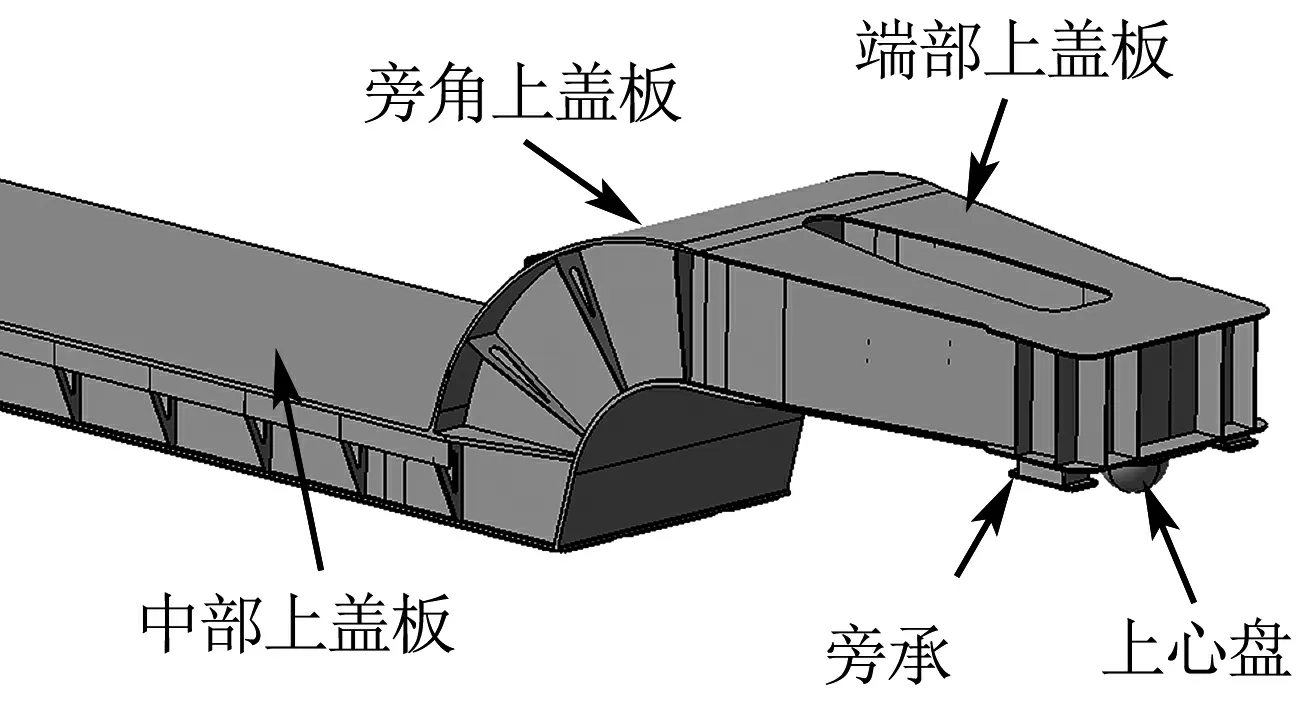
(a) 大底架

2 工况及评估依据

原铁道部发布实施TB/T 1335—1996《铁道车辆强度设计及试验鉴定规范》[2]，规定“专用车辆的强度设计，除特殊要求在设计任务书中加以载明外，均应符合本标准”.在较长一段时间内，我国铁路车辆的强度校核主要依据TB/T 1335—1996标准.

长大货物车作为铁路特种货车中的一大类车种，长期缺乏统一的行业标准，大多一直参照通用货车的设计标准，这是不合理的.此后，国家铁路局先后实施TB/T 2553—2018《铁路长大货物车》[3]、TB/T 3550.2—2019《机车车辆强度设计及试验鉴定规范车体 第2部分：货车车体》[4]，后者明确仅“适用于标准轨距铁路上运用的新设计一般用途货车车体结构强度的设计和试验鉴定”，其规范总则中亦对货车进行了定义：“用于运输货物的非固定编组铁道车辆属于本类(不包括长大货物车等特种货车)”.所以对于凹底平车车体强度的校核应该依据TB/T 2553—2018标准，参考TB/T 3550.2—2019标准.

标准TB/T 2553—2018中规定，长大货物车应按照第一工况和第二工况进行校核.该凹底平车车辆额定载重160 t，承载面长10 m，应用时一般列尾编挂，重车时限速，不涉及铁路驼峰调车情形，无须校核车辆结构的强度是否满足调车冲击载荷下的要求，也就无须使用第二工况校核[5].凹底平车静强度计算工况[6-8]见表1.

表1 凹底平车静强度计算工况

标准TB/T 2553—2018中定义了拉、压应力下的安全系数值，复合应力状态下一般使用拉应力下的安全系数值1.59进行校核；TB/T 3550.2—2019标准较TB/T 1335—1996标准增加了利用率和安全系数的要求，明确了货车车体常用材料安全系数，给出了Q345材料的第一工况安全系数(1.60)，第一工况许用应力216 MPa.对于低合金钢Q460E材料，标准中未明确给出第一工况许用应力值，参考文献中安全系数的计算方法[9]对零件工作条件系数、剩余应力影响系数、力与应力确定的正确程度系数都取1.1，对零件材料组织的均匀性系数取1.2，得到实际安全系数n=1.13×1.2=1.597 2，所以，Q460E材料的第一工况许用应力为460/1.597 2，取整为288 MPa.表1中的静强度计算工况中的最大应力均不得大于材料的第一工况许用应力.

3 模型及加载

大小底架之间通过心盘结构连接，受力较大，联合仿真容易出现接触非线性的不收敛性问题，故单独对大小底架进行强度计算.主要采用壳单元模拟，单位选用mm-t-MPa，大底架单元大小约为20 mm，小底架单元大小约为10 mm，厚度取设计值，心盘采用六面体单元模拟，整个大底架模型单元共691 844个，节点共684 958个，整个小底架模型单元共424 707个，节点共425 063个.

对于通过心盘传递的长大货物车，承载能力较弱，通常根据线路的动力学试验获得总载荷系数，然后以垂向载荷的形式进行实车加载.凹底平车车辆在设计阶段无法通过实车试验获取总载荷系数，且受试验条件、工况及线路影响，根据实测值换算得到的总载荷系数有效性亦有待考究.

垂向总载荷包括垂向静载荷、垂向动载荷和等效至垂向载荷的侧向载荷.垂向静载荷包括车体自重和货物重量；垂向动载荷由垂向静载荷乘以垂向动载荷系数而定，垂向动载荷系数参考TB/T 3550.2—2019标准及同类车型取0.2；侧向载荷由垂向静载荷乘以侧向载荷系数而定，侧向载荷系数参考TB/T 3550.2—2019标准取0.1.车体自重以加速度形式施加，货物的重量以质量单元形式均匀施加于大底架的承载面上.垂向加载时，约束大底架心盘和旁承处的垂向位移，约束小底架上心盘和旁承处的垂向位移.

依据TB/T 3550.2—2019标准，车体扭矩取为40 kN·m，使用公式M=(ΔP1+ΔP2)×b/2计算，式中，b为同一枕梁两支撑点之间距离，ΔP1、ΔP2分别为同一枕梁两支点承力的变化绝对值.在大底架的一个上旁承处施加40 kN·m /b大底架扭转载荷，同时约束其余三个上旁承处的垂向位移.在小底架的一个上旁承处施加40 kN·m /b小底架扭转载荷，同时约束其余三个上旁承处的垂向位移.

纵向拉伸、压缩载荷均沿车辆行驶方向作用于大底架的1位端心盘位置(拉伸、压缩的载荷方向相反)，约束1位端、2位端心盘位置和旁承位置处的垂向位移及2位端心盘位置的沿车辆行驶方向的位移.纵向拉伸、压缩载荷均沿车辆行驶方向作用于小底架下心盘位置(拉伸、压缩的载荷方向相反)，拉伸工况时约束小底架的牵引梁前从板座位置沿车辆行驶方向的位移、小底架上心盘和旁承位置的垂向位移，压缩工况时约束小底架的牵引梁后从板座位置沿车辆行驶方向的位移、小底架上心盘和旁承位置的垂向位移.

4 有限元分析

4.1 刚度计算

凹底平车承载面的长度较长，考虑到特种货物装卸的可操作性，要求承载面距离轨道的高度尽可能低，这将导致大底架两端心盘之间的距离较大[10-11]，所以，刚度值是评价车体性能的关键参数之一.参考TB/T 3550.2—2019标准，“垂向弯曲刚度试验用挠度与车辆定距之比值(挠跨比)来评定”，计算大底架在垂向静载荷作用下，挠跨比为61.6/20 950=1/340；小底架在垂向静载荷作用下，挠跨比为3.4/4 625=1/1 360，均满足设计任务书的要求[12].

4.2 强度计算

对大小底架原结构进行强度计算，底架局部应力云图见图2.分析结果表明：大底架的最大应力为225.6 MPa，位于折角区弯角过渡处的中间区域，已超过材料的许用应力.小底架的最大应力为204.6 MPa，位于中梁上盖板变截面处，已接近材料的许用应力.两种结构在相应区域出现最大应力的原因都在于该区域存在刚度不协调问题，从而导致应力集中.

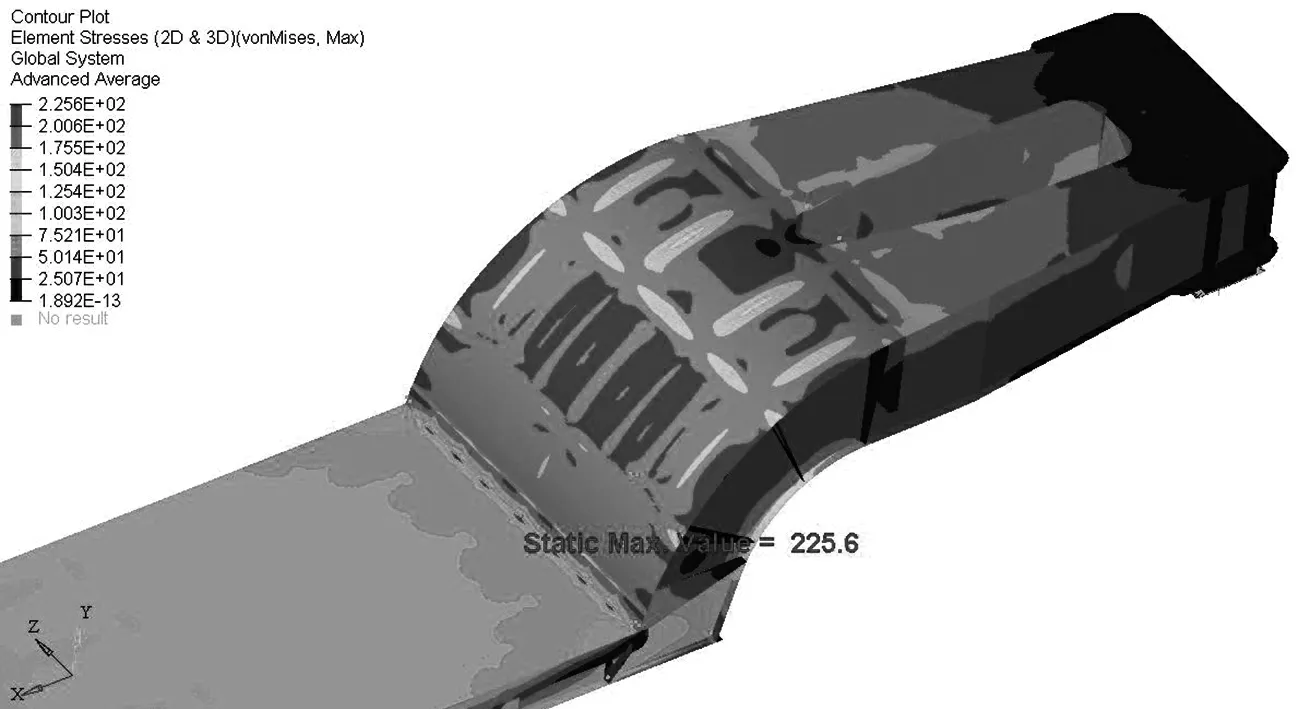
(a) 大底架

结构的刚度不协调问题是导致局部区域出现应力集中现象的主要原因.轨道车辆结构承受着复杂的拉伸、弯曲或扭转载荷的作用.在外载荷的作用下，结构的变形量与其自身刚度成反比.车辆承载结构具有显著的变截面特征，结构不同区域的刚度往往存在着明显差异.因此，在结构刚度急剧变化时，变刚度区域两侧的变形也会急剧变化.这时，在过渡区域均存在显著的应力集中现象.应力集中一般出现在靠近大刚度区域的刚度薄弱但变形显著的区域，且高应力区域的面积较小.

就所研究的大底架结构而言，其原始结构见图3(a).该结构设置了7块竖向隔板，除中部隔板厚30 mm外，其余隔板厚度均为25 mm.在垂向装载载荷的作用下，大底架绕横向轴弯曲.由于大底架端部区域的截面高度较大，而中部区域的截面高度较小，导致中部区域的弯曲变形较端部区域更大.竖向隔板能够有效增加端部区域的抗弯刚度，但也能导致端部结构在位于竖向隔板前缘的区域存在显著的刚度突变问题，并产生应力集中现象.竖向隔板的厚度越大，局部区域的刚度不协调问题越突出.基于此，结构优化通过改善局部区域的刚度不协调问题进行，优化结构见图3(b).优化结构将原有的7块隔板增加到8块，通过保证端部区域的抗弯刚度，使大底架结构的垂直弯曲变形与原始结构相当.非贯通隔板的厚度降低至16 mm，以协调其与中部结构邻近区域的刚度.通过这一优化措施，使大底架的最大应力降低到201.3 MPa，满足结构强度要求.

(a) 原结构

小底架高应力区域也存在因刚度不协调导致的应力集中.小底架枕梁上装设旁承，心盘与旁承共同支撑大底架结构.在旁承承载时，枕梁相对中梁绕纵向轴弯曲.由于中梁的抗弯刚度显著大于枕梁，因此，在原始结构的枕梁与中梁上盖板交界区域将产生明显的应力集中现象，见图4.优化结构将中梁与枕梁的上盖板制为一体，在边缘区域以大半径圆弧过渡，使两个抗弯刚度差异显著的结构实现平缓过渡，刚度变化协调.

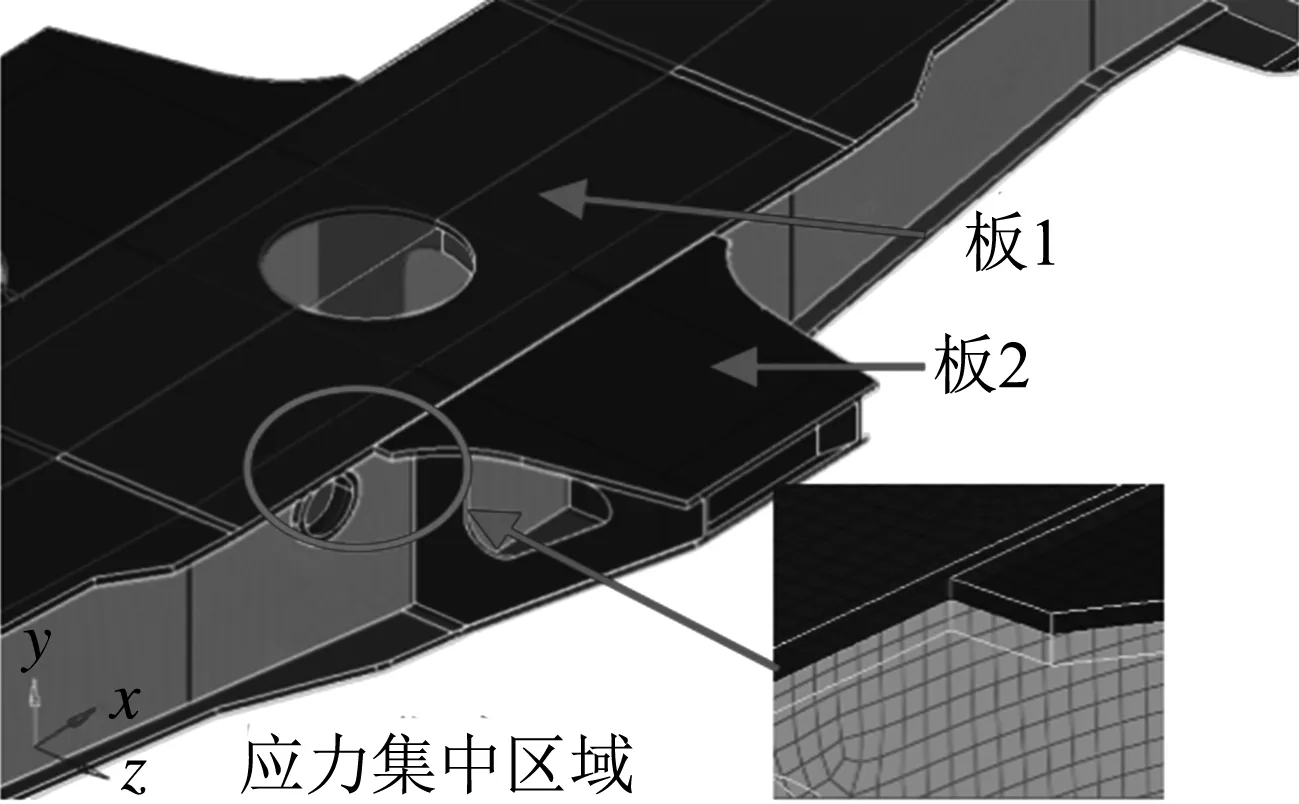
(a) 原结构

结构改进后大底架第一工况的应力均低于相应材料的许用应力，最大应力出现在压缩工况，为201.3 MPa，位于折角区弯角过渡处(图5(a)).小底架第一工况的应力均低于相应材料的许用应力，Q460E材料最大应力出现在拉伸工况，为212.6 MPa，位于中梁下盖板折角处(图5(b)).Q345E材料最大应力出现在压缩工况，为192.3 MPa，位于纵向腹板靠近牵引梁补板处(图5(c)).

从图5(c)的分析结果来看，该区域的应力降低到164.1 MPa.这一优化措施同样适用于承受弯曲载荷的局部结构与主结构之间的过渡，鱼刺形集装箱专用平车车体的横向梁与中梁间亦采用了这样的结构[13-14].此外，优化结构将存在高应力区域的焊缝优化为非焊接结构，能够显著改善结构的疲劳强度.

(a) 折角区弯角过渡处图5 大小底架改进后应力云图

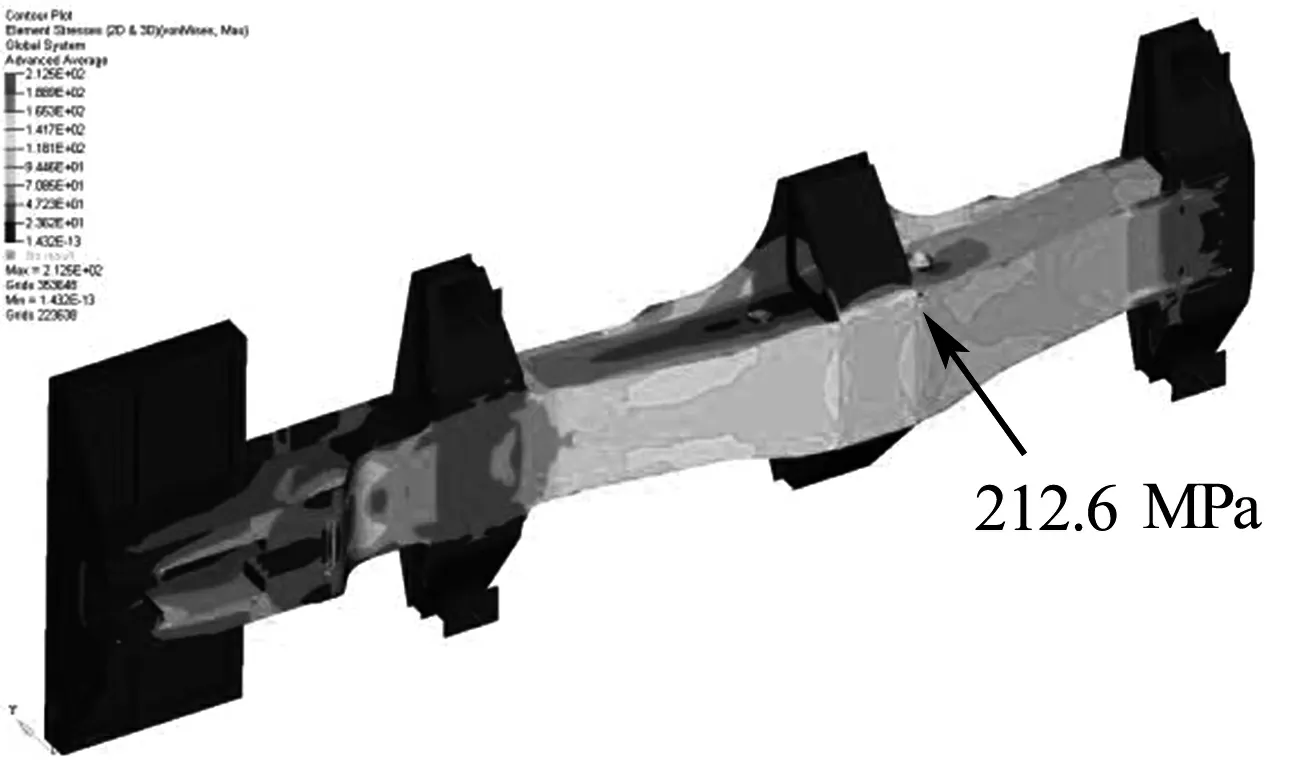
(b) 中梁下盖板折角处

4.3 模态计算

根据三维弹性动力学基本方程及力的边界条件，利用等效积分形式的伽辽金法，最终可以得到有限元格式下的动力学微分方程,该方程是车体振动分析的动力学基础.结构模态分析主要是预测无阻尼结构的自振频率和振型，因此微分方程可进一步简化为：

(1)

Kφ-ω2Mφ=0

(2)

选用工程上常用兰佐斯算法求解特征值问题，基本思想是将原特征值问题转化为三对角矩阵的特征值问题.求解式(2)可确定φ和ω，得到n个特征解：

式中：ω1，ω2，…，ωn为系统的n个固有频率，且0≤ω1<ω2<…<ωn.特征向量φ1，φ2，…，φn为系统的n个固有振型.则系统的固有频率：

(3)

所以，模态主要取决于所考察结构的质量分布以及所考察结构的边界约束(刚度)情况.

对凹底平车进行模态计算，主要是关注大底架的频率.一般情况下，按照实际结构进行有限元建模能够正确反映所考察结构的质量和分布，所以正确地施加边界约束是进行动力分析的先决条件，不适当边界约束将导致局部过刚，影响计算收敛速度及结果.

基于空载工况，建立如表2所示不同边界约束的模型1-5，对大底架的主要振型频率进行统计，见表3.对比模型1-2和3-5的大底架绕垂向一阶扭转频率可知，单独大底架模型明显高于大小底架耦合模型；对比模型1-2、模型3-5可知，不论单独大底架模型还是大小底架耦合模型，对模型心盘位置全简支约束或部分简支约束均不影响大底架的一阶扭转频率，但心盘位置的全简支约束相比于部分简支约束会明显提高大底架的垂向频率；对比模型3-5可知，大小底架耦合模型改变小底架的心盘约束方式，不改变大底架的一阶横向频率.

表2 不同模型边界约束情况

表3 大底架主要振型频率对比 Hz

如果从整车中单独取出大底架作为模态分析对象，边界条件只能简化为简支，然而真实情况是大底架安装在弹性的小底架结构体上，结合模型1-5大小底架的振型以及列尾编挂的实际应用场景，模态分析时需同时考虑大小底架结构，进行结构的综合模态分析，并关注这两个部件之间在低频段的自振频率耦合(共振)现象.

使用模型5的边界约束方式，通过有限元计算识别重载工况下的振型频率如表3模型6所示，各阶频率均较低，且低阶模态主要为大底架的模态，大底架、小底架在低频段没有自振频率耦合现象；相同振型时，空载工况下的模态频率均高于重载工况下的模态频率；空载和重载工况下，一阶模态的振型出现顺序相同且频率的递增趋势相近.

5 结论

本文使用有限元方法分析了凹底平车车辆大小底架的主要应力集中区域并提出了改进方法，改进后的第一工况最大应力均低于材料的许用应力，满足强度要求.详细介绍了强度计算工况的设置依据及有限元模型的加载方法，对比了不同约束边界下的大底架模态频率，识别出的大小底架在低频段没有自振频率耦合现象，可为类似产品的设计及计算提供一定的参考.