综合经典力学与有限元的汽车二维碰撞事故车速再现方法研究
2022-12-14曹弋陈龙飞何霖
曹弋,陈龙飞,何霖
(大连交通大学 交通运输工程学院,辽宁 大连 116028)
随着经济的快速发展,在当今社会公害中,道路交通事故赫然在列.汽车二维碰撞事故的普遍性、复杂性、严重性与不可逆特性,使得这类事故不但对人身财产安全有严重威胁,而且还存在难以认清事故情节、难以划分事故责任等问题[1].因此,有必要利用相关技术手段,对这类交通事故的再现分析方法开展研究.
目前国内外学者对该领域的研究可归纳为基于经典力学原理和有限元仿真分析两个方面.以经典力学原理为代表的研究:张晓云等[2]研究了人车碰撞中人的落地姿态、车辆初速度和人与地摩擦因数之间的关系,建立了人—地摩擦因数有效性模型;邹铁方等[3]以经典力学理论和若干假设为基础,研究了车辆后制动距离和行人抛距之间的相互关系,并建立了基于人车最终距离的碰撞车速估算模型;Ishikawa[4]在碰撞中心引入切向和法向恢复系数,逆向推导了事故再现模型;Zou等[5]基于经典力学理论和四组假设推导公式进行事故再现,并通过仿真试验验证其可行性;Lyu等[6]根据经典力学建立了碰撞部位碰撞角、变形和法向冲量之间的关系,研究了模型求解的曲面重构方法.以有限元仿真为代表的研究:王蕊等[7]根据有限元法建立了大客车与护栏模型,模拟大客车撞击护栏类的交通事故;张晓云等[8]借助有限元仿真,提出了人-地摩擦因数与法向力的函数关系;York等[9]提出了一种新的车辆碰撞仿真算法,该算法在求解过程中考虑了车辆碰撞产生的三维力,并实现了损伤轮廓的可视化,缩短了有限元仿真计算的时间;Fahlstedt等[10]建立有限元碰撞仿真模型,研究了碰撞角度和初始碰撞速度对再现分析结果的影响;Wach[11]提出车辆事故的重建需要根据工程和技术操作的特定系统的可靠性进行评估,利用贝叶斯网络,提出了车辆事故再现可靠性的形式化概念;王金刚等[12]研究了车辆正面碰撞变形能网格图在事故再现与车速计算中的应用;余松[13]通过求解变形能网格图和车辆速度之间的关系,求出车辆碰撞速度;Schelkle等[14]提出了乘员安全计算方法,采用有限元法对车辆碰撞进行了模拟,确定了乘员舱的首次加速度历程;吕继华[15]采用测量碰撞变形量和HyperMesh,建立了汽车有限元模型并进行了碰撞仿真分析.
综上所述,现有研究多基于某一理论体系或方法开展,尚未将经典力学与有限元进行有效结合.两种方法均具有局限性:经典力学方法无法分析碰撞变形,对弹性恢复系数等关键参数的取值具有一定的经验性;有限元方法的汽车初始碰撞速度难以确定,不便进行速度试算.鉴于上述问题,本文采用经典力学方法求解汽车碰撞接触瞬间速度,将其作为有限元碰撞仿真实验的初始速度参数;再利用有限元仿真实验进行有限范围内的速度试算,进而借助动量、能量及弹性恢复系数等参数进行结果验证.研究成果对事故再现分析理论的丰富与发展具有借鉴意义,对交通事故处理及认定责任具有现实应用价值.
1 经典力学模型
以碰撞点为原点建立坐标系.两车重心坐标分别为(a1,b1)和(a2,b2),碰撞冲量在X、Y轴方向上的分量分别为PX、PY.碰撞后两车的速度在X、Y轴上的分量分别为V1Xh、V2Xh、V1Yh、V2Yh,碰撞前速度在X、Y轴上的分量为V1Xq、V2Xq、V1Yq、V2Yq,两车碰撞前后的横摆转动角速度分别为ω1q、ω2q、ω1h、ω2h,两车回转半径为k1和k2,质量为m1和m2,碰撞损失能量为E,汽车碰撞示意图见图1.
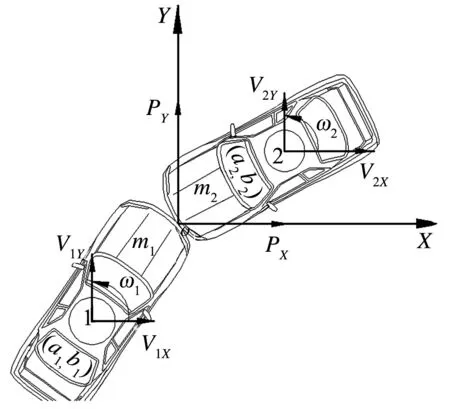
图1 汽车碰撞示意图
根据动量守恒与角动量守恒,可得式(1).
(1)
根据能量守恒可得式(2).
(2)
切向与法向弹性恢复系数,如式(3)所示.
(3)
2 汽车有限元模型
2.1 模型建立
本研究采用了已有的广汽丰田雅力士汽车有限元模型.分别利用Hypermesh软件进行网格划分、Ls-prepost软件进行前处理、LS-DYNA软件进行求解分析、Hyperview软件进行后处理.
对汽车模型进行网格划分.划分时既要保证求解结果的精确度,也要尽可能地减少分析时间,划分结束后会对网格进行检查,参照网格质量检查一般性规律,其中翘曲量不能超过5°;网格单元纵横比应小于5;扭曲角度控制在20°左右;当雅可比数值大于0.7,认为结果理想.材料赋予则需要根据车身不同部对有限元模型处理后,位的零件选取相应的材料,输入密度、泊松比、屈服应力、杨氏模量等相关参数,见表1,并确保车辆的质量与重心等与实际一致.
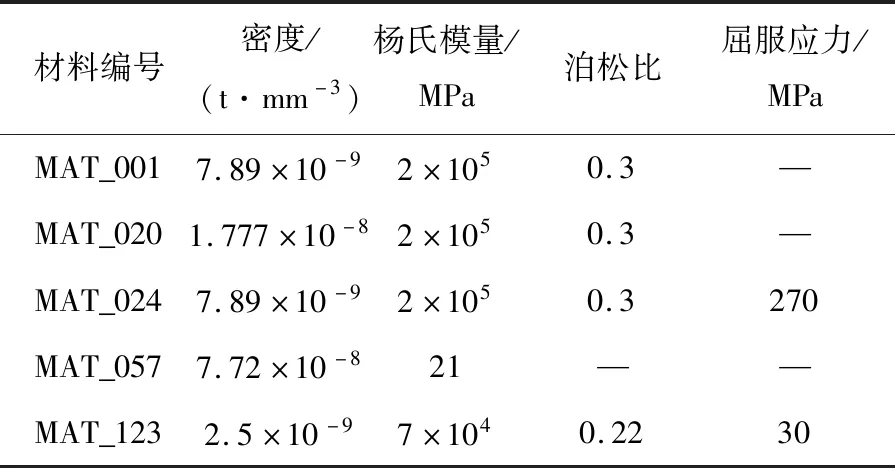
表1 主要材料参数设置
2.2 模型验证
对有限元模型处理后,需要验证汽车模型的准确性.采用C-NCAP汽车100%重叠刚性壁障碰撞试验进行验证.汽车以56 km/h的速度碰撞刚性壁障,最终碰撞仿真结果见图2.输出的车辆速度和能量变化曲线见图3.

图2 实车碰撞与仿真碰撞

(a) 速度
根据图3可以看出,车辆动能在0.067 s时达到最低,由初始的0.159×109J降低到0.005×109J,即速度为零时,能量损失为0.154×109J.根据动能定理计算可得车辆动能变化量为0.148×109J.两者之间能量误差为5.705×106J,占总能量损失的3.7%,在误差允许范围内,可以认为汽车有限元模型是合理的.
对车辆和刚性壁作用力进行分析,对X、Y、Z三个方向和总的作用力进行分析,见图4.
从车辆和刚性壁之间的相互作用力可以看出,X方向为其主要受力方向,与总的作用力相同或者相反.Y和Z方向在0值上下波动着.
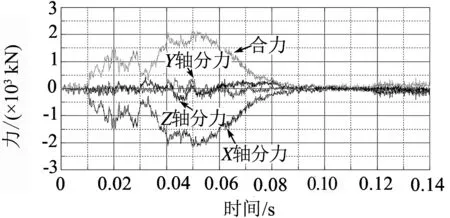
(a) 车辆受力
3 经典力学与有限元结合法
根据事故现场与车辆残留痕迹,如制动痕迹、散落物抛落位置及变形部位与形状等,初步确定车辆碰撞位置及角度.依据经典力学原理求解出车辆碰撞前的速度,将该速度代入有限元模型中.通过碰撞仿真实验,对比实际变形量与仿真变形之间的误差.通过对碰撞角度、碰撞速度、碰撞位置等参数的连续调试,使实际变形与仿真变形相符.最后输出有限元法得出的车辆速度变化曲线,并得出碰撞前后车辆速度.再根据动量、能量及弹性恢复系数关系验证最终求解的速度,经典力学与有限元结合法流程图见图5.

图5 经典力学与有限元结合法流程图
4 事故案例分析
4.1 事故概况
某日交叉路口上,一辆从西向东行驶的本田飞度轿车(甲车),与从南向北行驶的哈飞路宝轿车(乙车)发生侧面碰撞,事故造成多人受伤,车辆受损严重.发生事故时,汽车轮胎与道路的附着系数为0.70[16].事故过程示意图见图6.

图6 事故过程示意图
对事故现场的汽车型号进行确定,然后根据汽车型号查找汽车的相关尺寸,见表2.
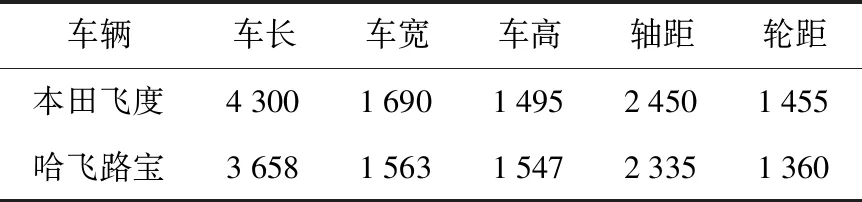
表2 两车参数 mm
4.2 参数定义
根据事故现场留下的制动痕迹及车辆碰撞后最终的停止位置,使用PC-Crash仿真模拟.首先对事故现场相关参数进行设置,如事故位置参数、车辆参数等.然后进行仿真模拟,通过不断调整事故车辆的碰撞点、碰撞角度、转向角度、碰撞速度等相关参数,使得碰撞模拟的运动轨迹和最终停止位置与实际终止位置一致,停止仿真碰撞的模拟.车辆轨迹及最终位置模拟见图7.
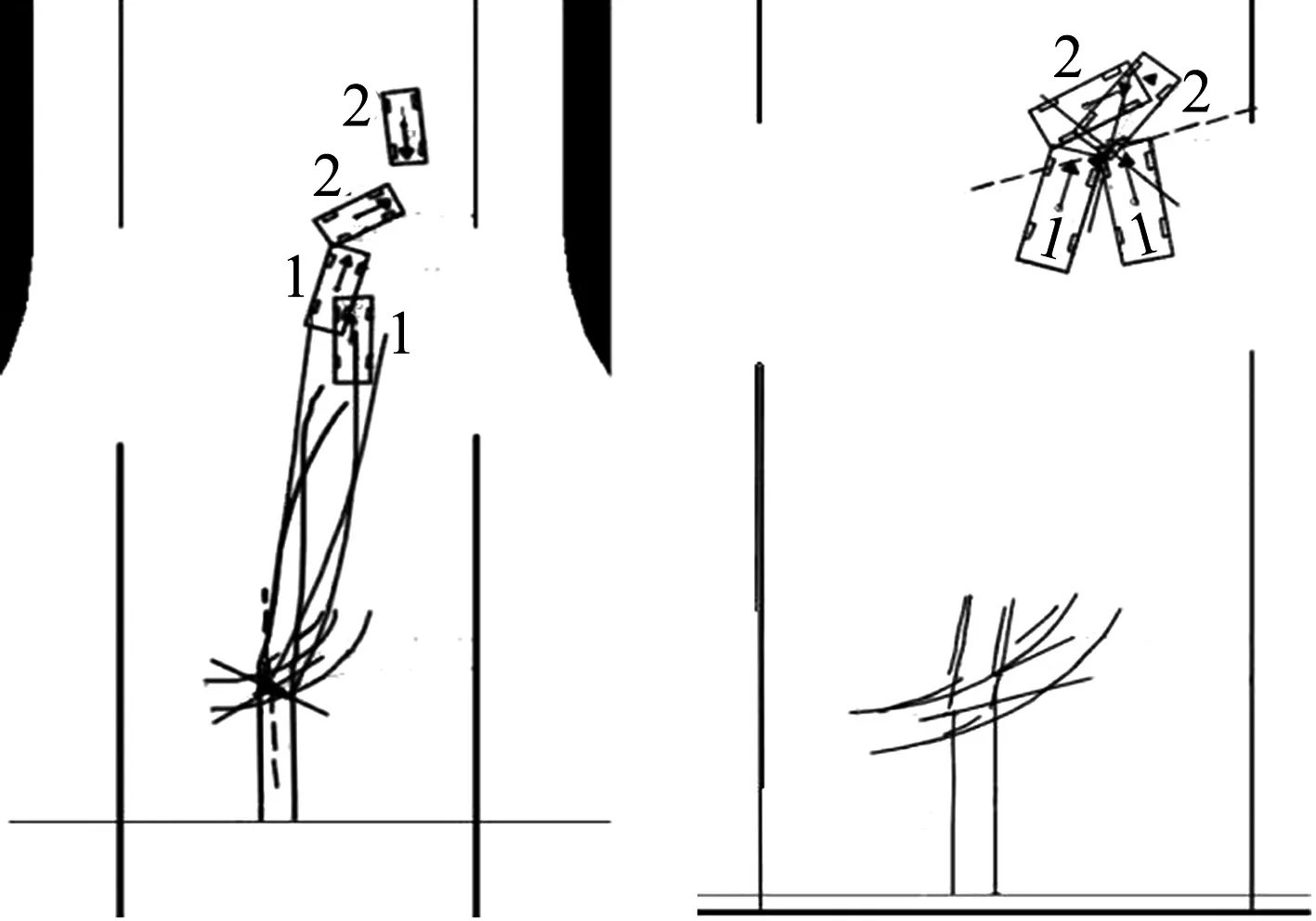
图7 车辆轨迹及最终位置模拟
经PC-Crash仿真分析,两车碰撞前速度分别是V1=44.57 km/h,V2=56.3 km/h,两车相对东西方向的角度分别是19°和89.9°.将上述速度、角度作为初始参数代入到有限元模型中,进行有限元仿真分析.对仿真输入的碰撞速度、碰撞角度以及碰撞位置等参数不断调试,直到仿真变形与实际仿真变形相符,导出最后的仿真结果.
4.3 模拟结果
有限元仿真与实际发生事故汽车变形比较,见图8.输出两车碰撞前后速度以及能量变化,见图9.
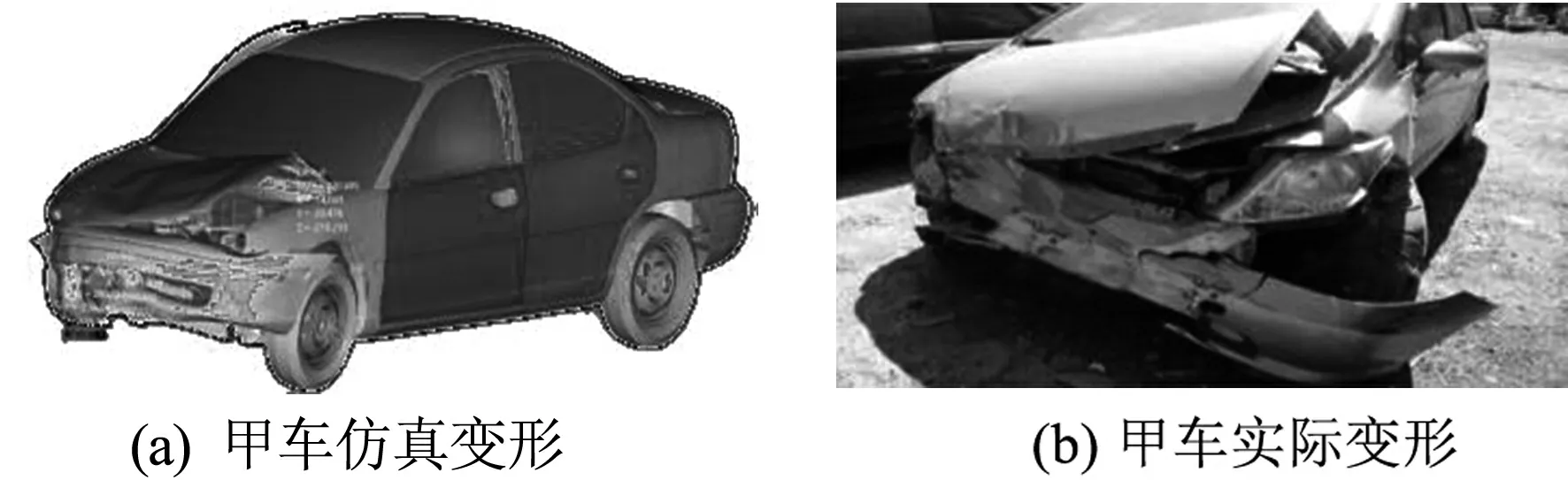
图8 仿真变形与实际变形对比分析

(a) 甲车速度
从速度变化曲线可以得出,两车碰撞前速度分别为V1Xq=11.63 m/s、V1Yq=-4.23 m/s、V2Xq=0 m/s、V2Yq=-15 m/s、V1Xh=6.3 m/s、V1Yq=-11.3 m/s、V2Xq=5 m/s、V2Yq=-12.5 m/s.由于碰撞前两车沿着直线运动,所以假定两车碰撞前横摆转动角速度分别为ω1q=0和ω2q=0.由现场参数收集和调查可得,两车质量为m1=1 190 kg和m2=1 225 kg,两辆汽车的质心坐标分别为(-1.28,0)和(0.78,0),两车回转半径分别为k1=1.28、k2=1.09.根据式(1)计算可得两车碰撞后角速度分别为ω1h=-5.52和ω2h=-18.05.根据式(2)计算可得碰撞过程损失的能量E=80.998×106J,从能量变化曲线图(图9(c))也可以得出内能变化量为81×106J,两者相差无几.进而根据式(3)可以推导出两车的切向和法向恢复系数分别为eX=0.111 8和eY=0.834 3.对比实车碰撞后求解的恢复系数,两者相符.结果对比分析见表3.

表3 结果对比分析
5 结论
(1)与PC-Crash软件及有限元模拟结果相比,汽车二维碰撞事故再现的经典力学与有限元结合法分析所得车辆碰撞接触瞬间速度与总能量损失的误差均在5%以内.
(2)经典力学与有限元结合法充分利用了事故车辆的碰撞变形特征数据,改善了事故再现结果的可信度;同时借助经典力学的初步计算,可在初始碰撞速度相对明确的条件下进行有限范围的试算与变形量比对,提升了正向模拟分析的效率.
鉴于事故详细资料获取的困难性,本研究仅对少数事故案例进行了多方法再现分析,并从中挑选有代表性的事故案例进行说明,研究结果尚缺乏普适性检验.尽管如此,本研究所提出的一般性方法与规律性结论仍可为其他同类研究所借鉴.事故案例数量不足的问题,可在后续研究过程中逐步积累完善.
致谢:本文受2021年度大连交通大学专业学位研究生质量攻关项目和2021年度大连交通大学教学改革研究立项项目资助,特此致谢!
