联体泵马达补油流量的分析与理论计算
2022-12-13侯明江刘晓玲
岳 崧 田 璐 侯明江 刘晓玲 李 斌
(中国航发西安动力控制科技有限公司,陕西 西安 710077)
0 引言
联体泵马达是由变量柱塞泵(简称泵)、定量柱塞马达(简称马达)、补油阀、伺服控制机构及安全溢流阀等共同组成的一个闭式静液压传动装置,用于将发动机输出的机械能经泵转化为液压能,再经马达将液压能转化为机械能,实现能量的传递和无级调速,广泛应用于履带式车辆转向系统中。联体泵马达中设置了补油油路,用以补充泵和马达内泄漏所消耗掉的油液,并维持低压侧的压力,同时轴承和球碗保持架组件的润滑油液也由补油油路提供,因此补油对联体泵马达非常重要,补油流量则是判断产品是否合格的一个重要指标。
1 补油流量的需求与影响
1.1 补油流量的需求组成
某型联体泵马达液压原理简图如图1所示。泵的进出油通过壳体中的油道直接与马达相连接,构成一个静液压闭式回路,简化了连接管路。通过伺服控制机构来改变泵的变量,进而改变主油路中液压油的流量和方向,实现马达的变速和换向。补油油液通过补油进口进入闭式回路中,一是向四个喷嘴供油,为轴承和球碗保持架组件润滑;二是从补油阀流入低压侧油道,补充泵和马达内泄漏流量损失,维持低压侧油道的压力,防止吸空现象的产生。
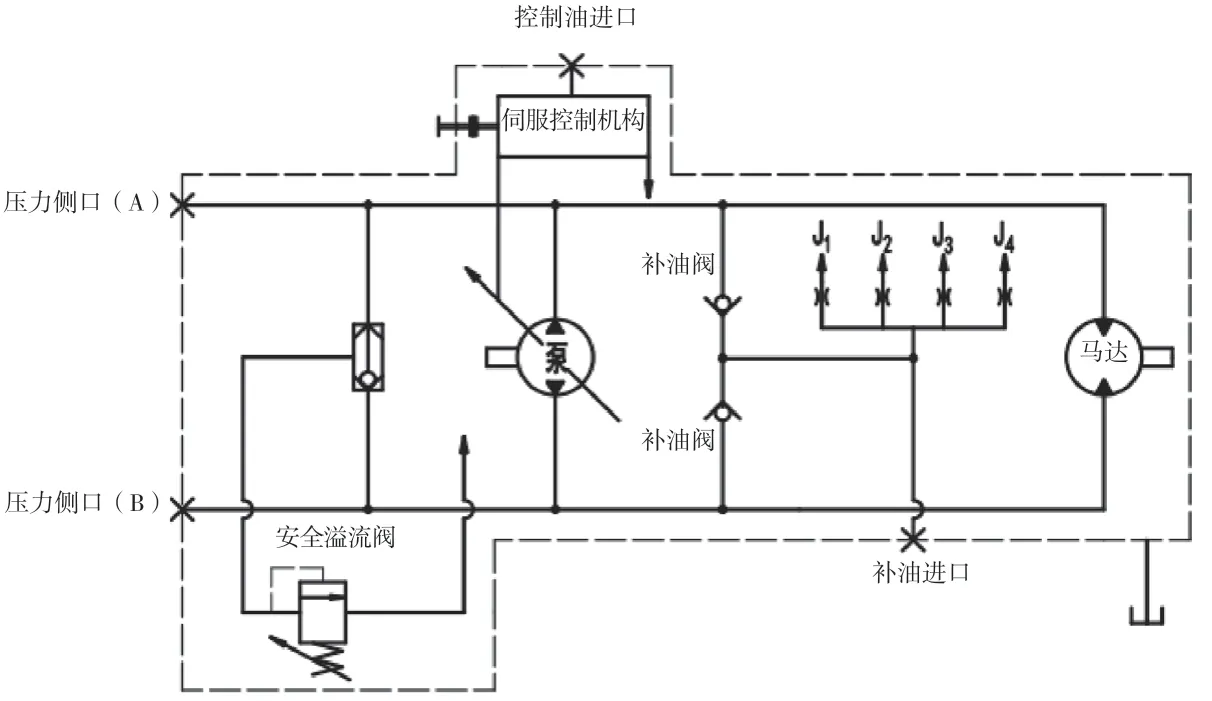
图1 联体泵马达液压原理简图
当工作压力未达到安全溢流阀设定压力时,总补油流量为四个喷嘴的通流流量与流入低压侧的流量之和,如公式(1)所示。

式中:QB为补油总流量;QJ1、QJ2、QJ3和QJ4分别为四个喷嘴通流流量;QL为补入低压侧油腔流量。
1.2 各需求部分对补油流量的影响
四个喷嘴结构图如图2所示,满足薄壁孔口流量计算:当孔口的壁厚LJ小于孔径dJ的1/2,且孔口边缘是无倒角的锐缘时,孔口出流的流体仅与孔口边缘相接触,此时孔口就可认为是薄壁锐缘孔口,其流量如公式(2)所示[1]。

图2 喷嘴J1~J4简图
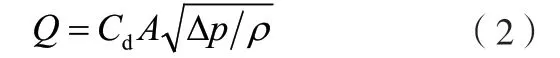
式中:Q为喷嘴通流流量,m3/s;Cd为流量系数;A为喷口面积,m2;∆p为喷嘴孔口压差,Pa;ρ为油液密度,kg/m3。
喷嘴孔口压差为补油压力与壳体回油压差,忽略管道压力损失和壳体回油压力,孔口前后压差即为补油压力值。当补油压力稳定时,则通流流量为定值,它不随工况的改变而发生变化。
由于泵和马达内部相互运动的结合部均为间隙配合,因此工作中必定会产生一定的内泄漏,即存在容积效率,补入低压侧中的油液即泵和马达内泄漏之和如公式(3)所示。

式中:QP为泵内泄漏流量,m3/s;QM为马达内泄漏流量,m3/s;V为联体泵马达排量,mL/r;ηP为泵容积效率;ηM为马达容积效率。
由泵和马达特性可知,随着转速和压力的提高,内泄漏流量增大,因此联体泵马达总补油流量将增大。
2 泵和马达泄漏流量分析
为了进一步分析泵和马达的容积效率,下面对泵和马达的泄漏机理进行详细的分析。由于该回路中泵与马达的排量相等,核心组件结构完全一致,因此泄漏的机理是相同的,下面以泵为例进行内泄漏的分析与计算。
如图3所示,在实际工作中,泵在柱塞和缸体孔、滑靴和斜盘、配流盘和缸体配流端面3对运动副缝隙之间均存在油液泄漏,分别记为q1、q2和q3,则QP=q1+q2+q3。由于上述3对运动副缝隙流动的Re一般较小,流态为层流,因此层流理论适用于该文的泄漏量分析[2]。
2.1 柱塞和缸体孔之间泄漏
如图3所示,油液在缸体孔和壳体之间形成压力差,使缝隙内形成压差流。柱塞与缸孔间实际流场的情况是柱塞与缸孔两端发生接触,即完全偏心,但在缸孔的中点位置柱塞与缸孔完全同心。柱塞相对缸孔有相对速度,柱塞的密封长度L是随柱塞在缸体孔内的位置而变的[3]。在既考虑了柱塞偏心问题,又考虑了柱塞密封长度变化的情况下,推导出的单柱塞和缸体孔的泄漏流量公式qx1如公式(4)所示。

式中:d为柱塞直径,m;δ为柱塞与缸孔单边缝隙高度,m;∆p为缸孔油压与壳体回油压差,Pa;μ为油液的动力黏度,Pa·s;L为柱塞留在缸体最大长度,m;Df为缸孔分度圆直径,m;γ为斜盘最大摆角,°。
柱塞在随缸体旋转一周时,一半时间处在吸油侧,一半时间处在排油侧。忽略吸油侧泄漏时,z个柱塞与缸体孔之间泄漏总量如公式(5)所示。

2.2 滑靴与斜盘之间泄漏
如图3所示,通过柱塞中心的阻尼孔将排出侧的压力油引入滑靴底面的油室,在结构上,油室外圈是环形的密封带,在密封带与斜盘间形成极薄的油膜[4]。滑靴油室的压力和壳体回油压力使缝隙h1内产生压差流,根据流量连续性原理可知,滑靴与斜盘缝隙间泄漏流量与柱塞中心阻尼孔通流流量相等,因此由平行圆盘缝隙流量公式和细长孔流量公式可得单个滑靴斜盘缝隙泄漏量qx2,如公式(6)所示。

图3 泵主要摩擦副及相关尺寸

式中:h1为滑靴与斜盘之间缝隙(油膜)厚度,m;d1为柱塞中心阻尼孔直径,m;r1、r2为滑靴密封环内、外半径,m;L1为柱塞阻尼孔长度,m;∆p为缸孔油压与壳体回油压差,Pa。
工作中滑靴随缸体旋转一圈只有一半时间处在排油侧。忽略吸油侧的泄漏流量时,z个滑靴与斜盘之间的泄漏总量q2如公式(7)所示。

2.3 配流盘与缸体之间泄漏
配流盘简图如图4所示,缸体与配流盘构成的配流副体现在缸体紧贴配流盘回转,以周期性地向吸油侧和压油侧配流。配流间隙内的液体形成液压油膜来保证配流副的压力场、速度场的平衡,泄漏主要是从腰型槽流出的液体[5]。根据层流理论,可得配流盘与缸体之间的泄漏流量q3,如公式(8)所示。

图4 配流盘简图
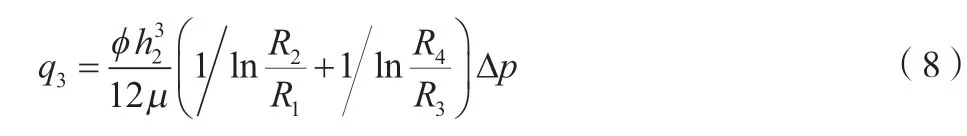
式中:ϕ为配流盘压力区包角,rad;h2为配流盘与缸体之间缝隙(油膜)厚度,m;R1、R2为配流盘内密封环内、外半径,m;R3、R4为配流盘外密封环内、外半径,m;∆p为配流盘腰型槽与壳体回油压差,Pa。
3 补油流量范围分析
通过以上分析可知,联体泵马达的补油总流量随工况的变化而变化,而变化的实质是泵和马达在不同的工况下内泄漏流量不同,即容积效率不同。由于零件在生产制造过程中存在一定的尺寸公差范围,产品在装配过程中也会存在一定的装配间隙范围,因此在同一工况下,联体泵马达的补油流量也是存在一定范围的。在产品进行试验时,通过在补油进口安装流量计便可测量出实时补油流量,将其作为判断产品是否合格的一个重要性能指标。一般情况下只需要计算额定工况下的补油流量范围即可。
3.1 补油流量的最大值分析
在额定工况下,泵和马达的容积效率是根据工作需求来设计确定的,同样也可参考泵和马达的相关标准的规定值来确定。当泵和马达工作在容积效率最低值时,相对应的泄漏流量为最大值,即QL(max)=Vn10-3[1-ηP(min)ηM(min)]。同时考虑喷嘴喷口直径加工公差,喷口直径取最大值,由公式(2)可知喷嘴通流流量最大,于是便可计算出联体泵马达补油流量的最大值。
3.2 补油流量的最小值分析
在工作中,泵和马达的功率损失主要是摩擦副的泄漏流量功率损失和摩擦功率损失,当这两者功率损失之和最小时,泵和马达的总效率最高,此时泵和马达对应的泄漏流量为最小值。满足泵和马达工作在最高效率时的条件是滑靴和斜盘、配流盘和缸体之间的油膜工作在最佳油膜厚度上,下面详细介绍这两种最佳油膜厚度的求解方法。
先来分析滑靴的泄漏流量功率损失。由于泵在工作过程中是(z-1)/2和(z+1)/2个柱塞交替处于压油过程,因此取z/2个柱塞处于压油过程来计算滑靴处的漏损流量∆Q[6],忽略回油压力,漏损功率如公式(9)所示。
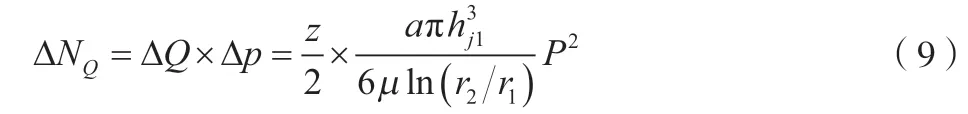
式中:a为压降系数;hj1为滑靴与斜盘之间的最佳油膜厚度,m;P为压油压力,Pa。
z个滑靴的摩擦功率损失如公式(10)所示。

式中:Fh为滑靴密封面摩擦力,N;υ为滑靴绕泵轴旋转的平均圆周线速度,m/s;S为滑靴密封环带面积,m2;ω为滑靴绕泵轴旋转角速度,与缸体角速度一致,rad/s;Rf为滑靴的分布圆半径,取缸孔分布圆半径为,Df/2,m。
总功率损失∆N=∆NQ+∆NF,最小功率损失的条件为d(∆N)/d(hj1)=0,于是便可以求出最佳油膜厚度,如公式(11)所示。
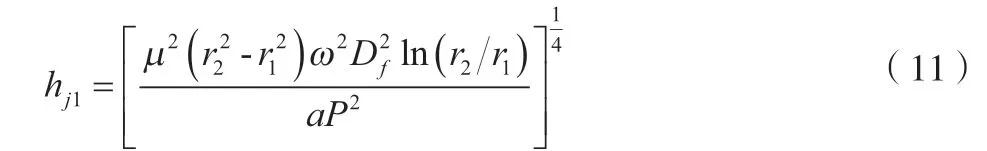
同理,配流盘与缸体配流端面泄漏功率损失如公式(12)所示。
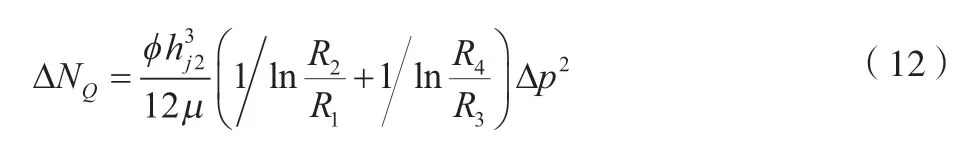
式中:hj2为配流盘与缸体之间最佳油膜厚度,m。
如图4所示,配流盘与缸体配流端面摩擦功率损失由3个部分组成,分别是内密封带摩擦功率损失、外密封带摩擦功率损失和两处吸油、排油间隔带摩擦功率损失,因此总摩擦功率损失如公式(13)所示。

式中:ω为缸体旋转角速度,rad/s;θ0为吸油、排油窗口间隔角,rad。

根据以上分析,当其他各参数已知时,可以计算出泵在最佳油膜厚度下的泄漏流量QPJ。
由于系统中马达和泵的摩擦副尺寸是一致的,计算出的理论泄漏流量相等,即QL(min)=2QPJ。同时喷嘴喷口直径取最小值时,便可计算出联体泵马达在额定工况下的补油流量最小值。
4 结论
该文主要通过由泵和马达的最小容积效率来确定内泄漏流量的最大值,同时对泵和马达的泄漏机理进行了分析,通过最佳油膜厚度的计算来确定内泄漏流量的最小值,并考虑喷嘴喷口直径公差的影响,最终建立起补油流量的数学模型,得出补油流量的理论范围。以上的分析和计算具有以下几方面实际意义:1)可指导产品试验验证,在产品试验中, 通过对补油流量的测量,将其作为判断产品是否合格的一个重要指标。2)可指导试验系统中补油流量的参数设置。3)可指导泵和马达摩擦副结构参数的优化设计。
