重型车辆作用下钢栈桥振动响应对比分析

殷新锋， 陈诚， 晏万里

(长沙理工大学 土木工程学院， 湖南 长沙 410114)

车辆行驶通过桥梁时产生激励导致车辆和桥产生相互振动，这种振动称为车桥耦合振动。钢栈桥作为一种运输物料、重型设备及人员而修建的临时结构，在工程建设中起到很重要的作用。已有众多学者对钢栈桥力学性能进行了大量研究，如谢晓鹏等采用通用有限元软件ANSYS，简化钢栈桥桩顶梁形式，将复杂的工字钢截面简化为矩形截面，对比分析发现2种截面形式下钢栈桥的力学性能差别不大，在进行有限元建模时钢栈桥桩顶梁截面形式可以简化；刘永锋采用ANSYS软件，根据工程特点及荷载情况，对一种皮带栈桥进行结构强度、稳定性验算，通过对栈桥各组成结构的分析，发现各类型杆件相互作用较小；殷新锋等基于LS-DYNA程序，将车辆子系统与桥梁子系统联立耦合形成显式车-桥耦合振动分析模型，验证了该车桥耦合方法的正确性。以上研究多是分析静载作用下钢栈桥的力学性能。钢栈桥作为一种临时通行设施，动载作用下性能特别是移动重载作用下力学性能尤为重要。本文以一座钢栈桥为工程背景，采用ANSYS软件建立桥梁模型，通过LS-DYNA程序建立显式车-桥耦合振动系统并结合实测值验证该系统的精确性，最后进行105 t重车作用下钢栈桥振动响应分析。

1 车辆模型的建立

1.1 车辆概况

重型车辆采用大件运输车辆，其由牵引车、叶片升举板和叶片组成，总质量105 t，车辆外形尺寸见图1。牵引车前轴和中轴轴距L1为2.98 m，中轴和后轴轴距L2为1.37 m，后轴与挂车第一轴轴距L3为9.2 m，挂车车轮之间的轴距L4、L5均为1.55 m，总长度为19.75 m；牵引车横向轴距L6、L7为1.80 m，挂车横向轴距L8、L10为0.74 m，L9为1.06 m。车辆轴重如下：P1=11.0 t；P2=15.5 t；P3=15.5 t；P4=21.0 t；P5=21.0 t；P6=21.0 t。

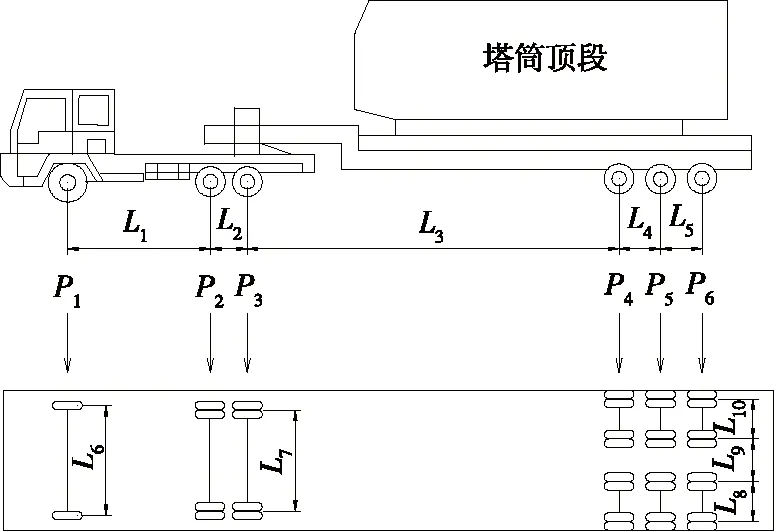
图1 车辆外形尺寸示意图

1.2 车辆模型的建立

为了使有限元数值模拟分析趋近于现实中重型车辆通过钢栈桥的情形，基于LS-DYNA程序建立105 t车辆模型。通过CAD软件中的HyperWorks建立105 t重车几何模型，运用其内嵌的HyperMesh模块对重车模型进行网格划分，最后保存k文件。通过LS-DYNA前处理软件LS-PREPOST对重车模型进行关键字修改，包括车轮、悬架系统等汽车细部构造。105 t重车有限元模型见图2。

图2 重车有限元模型

车轮由轮胎、轮毂、车盘组成。为真实地模拟轮胎与桥面的接触，轮胎采用线弹性橡胶材料，轮盘和轮毂采用线弹性刚性材料，整个车轮的各组成部分均为刚性连接。车轮压力在LS-DYNA中通过关键字*AIRBAG_SIM_PLE_AIRBAG_MODEL来定义，定义轮胎中的气体压力为0.8 MPa。车轮模型组成见图3。

图3 轮胎构造

采用壳单元、刚体、弹簧阻尼单元和多点约束模拟悬架系统，悬架系统的弹簧和阻尼器参数参考文献[10]确定。悬架系统见图4。

图4 悬架系统

通过定义关键字*INITIAL_VELOCITY_CENER_ATION来设置车轮的转动和平动速度、汽车运动状态及轨迹。

1.3 车辆模型的验证

车辆模型的正确性关系到车桥耦合试验结果的精确性。为验证车辆模型的正确性，对实车与有限元车辆模型各轴载值进行对比。

为得到车辆模型各轴轴重，通过定义关键字*DAMPING_GLOBAL对车辆模型施加全局阻尼，使车辆在移动过程中能快速趋于稳定，最后读取车辆各轴与桥面的接触反力(见图5)。轴载计算值与实车轴重对比见表1。

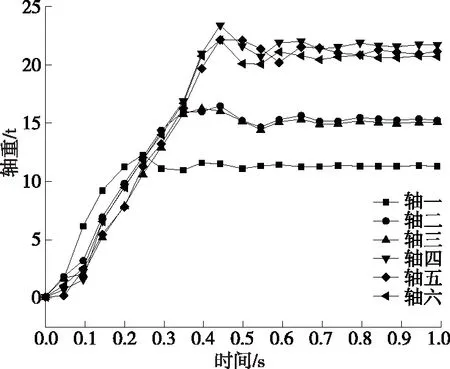
图5 车辆各车轴轴载时程曲线

表1 车辆模型轴载与实际轴载的比较

从表1可以看出：有限元重车模型模拟的轴载与实际轴载分布情况偏差较小，总质量偏差仅为0.67%，有限元车辆模型能真实地模拟重车的轴重分布。

2 桥梁模型

2.1 桥梁概况

某钢栈桥总长153 m，单跨跨径为9 m，桥面板宽6 m、厚10 mm，分配梁横向长6 m，每隔35 cm布置一根分配梁，分配梁采用I20a；主梁桁架采用双排单层3组贝雷梁，跨径9 m；桩顶承重梁采用2I40b，横向焊接为一体；桩基采用φ529钢管桩，每墩3根桩基，纵桥向间距9 m，横桥向间距2.6 m；桩长根据地质情况确定，不满足入土6 m时引孔，引孔深度4 m。图6为钢栈桥实图，图7为钢栈桥立面图。

图6 钢栈桥实图

图7 钢栈桥立面图(单位：cm)

2.2 桥梁三维有限元模型的建立

考虑到钢栈桥节点数量繁多且重复，钢栈桥各跨之间连接方式采用铰接，各跨之间的影响不大，建立四跨桥模型能反映105 t重车通过钢栈桥时钢栈桥的振动响应。此外，鉴于模型过于累赘会使计算时长成倍增加，在保证计算结果准确性的前提下合理简化桥梁模型。

利用有限元分析软件ANSYS建立初始单跨钢栈桥模型，再将ANSYS模型转为k文件导入LS-PREPOST，在LS-PREPOST中对模型进行一些关键字的定义，得到四跨钢栈桥模型(见图8)。

图8 四跨钢栈桥模型

2.3 有限元桥梁模型验证

为检验有限元桥梁模型的精确性，对模型进行静载试验，并将试验结果与现场实测值进行对比。限于篇幅，只给出一种工况下的对比结果，且仅对单跨下弦杆跨中节点进行分析。同时，在保证对比结果严谨性的同时，简化加载级数，仅加载一级，即对钢栈桥只作用一辆载重卡车，以减少数值模拟耗时。

后来姑父在城管给他找了个临时工，做市场管理员，工资不高，二千多，比玉敏少了三分之一。姑妈嫌工资少了，姑父说，指望工资吃饭喝西北风啊。姑妈顿悟，同意让小虫干市场管理员了。事实证明，小虫虽然文化不高，但智商不低，姑父什么也没指点，他竟无师自通，不但自己吃喝不花钱，连姑妈家吃菜他都管着。姑父对姑妈说小虫是块料子，就是文化低了，否则前途无量。

正式试验之前，先进行预加载，消除非弹性变形，以得到更真实的试验数据。测点布置见图9，静载试验现场见图10，静载试验结果与有限元计算结果对比见表2。

图9 测点布置

图10 静载试验现场

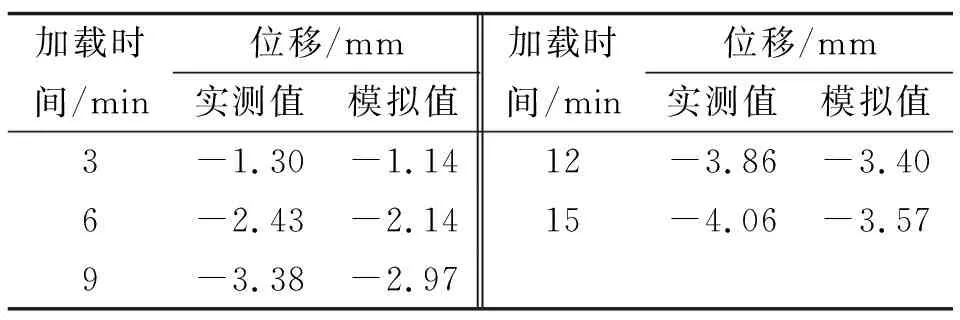
表2 跨中下弦杆节点位移

从表2可以看出：静载试验下单跨跨中下弦杆节点位移实测值为-4.06 mm，数值模拟值为-3.57 mm，相同加载时间内，模拟值为实测值的88%左右。根据结构力学，结构变形与施加的体外力、结构截面面积和弹性模量有关。这次静载试验和数值模拟的体外力相同，由试验车提供，下弦杆截面面积相同，两者变形存在差异的原因可能是钢栈桥经过长年使用其弹性模量降低。

为验证上述猜测，将有限元模型的弹性模量降低12%，通过LS-DYNA模拟动载试验，将模拟值与现场动载实测值进行对比。动载试验用车辆为一辆35 t自卸车，其前轴重为7 t，后轴重为28 t。试验车慢速(10 km/h)行驶通过钢栈桥，记录跨中下弦杆节点位移。图11为动载试验现场。

图11 现场动载试验

通过LS-DYNA程序中关键字*CONTACT_AUTOMATIC_SURFACE_SUAFACE实现车桥耦合，考虑到计算时间及试验车长度，将桥梁模型进一步简化，得到双跨车-桥耦合系统。除简化桥模型外，其余各条件均与现场动载试验相同。跨中下弦杆节点振动位移实测值与修改弹性模量后数值模拟值的比较见图12。

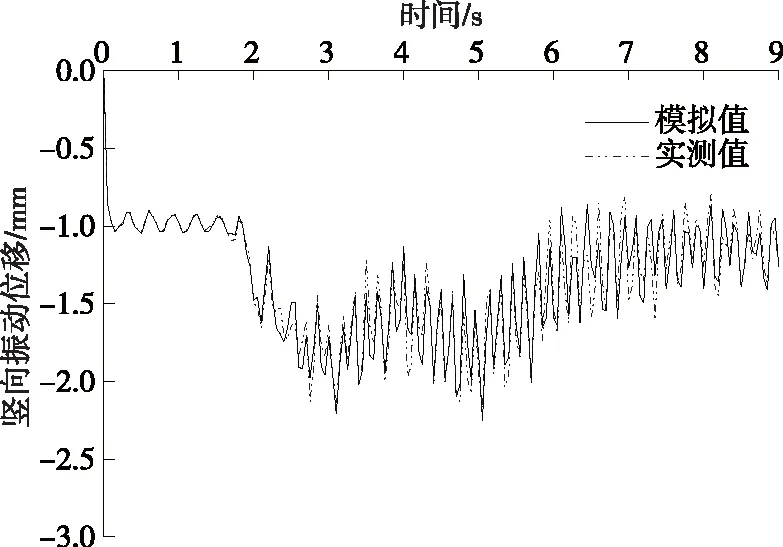
图12 动载作用下跨中竖向位移对比

从图12可以看出：修正弹性模量后的数值模拟结果与实测值的振动轨迹几乎一致，说明钢栈桥经过长年使用刚度出现下降，降低12%弹性模量后建立的LS-DYNA桥梁模型与实桥吻合。

3 重车作用下钢栈桥振动响应分析

3.1 荷载工况

通过LS-DYNA程序中关键字*CONTACT_AUTOMATIC_SURFACE_TO_SURFACE将105 t重车与钢栈桥耦合，形成四跨显式车-桥耦合振动分析系统(见图13)。

图13 车桥耦合系统

设置2种工况分析车辆质量和车速对钢栈桥振动响应的影响。工况一：一辆54 t重车以15 km/h的速度匀速驶过钢栈桥，一辆105 t重车以15 km/h的速度匀速驶过钢栈桥。通过关键字*MAT_RIGID改变材料密度实现重车质量的改变(通过这种方式改变质量不会改变车辆的轴重比)。

3.2 钢栈桥振动响应分析

3.2.1 动位移对比

2种工况下钢栈桥下弦杆跨中节点竖向振动位移对比见图14、图15。

图14 车辆质量对钢栈桥下弦杆跨中节点竖向振动 位移的影响

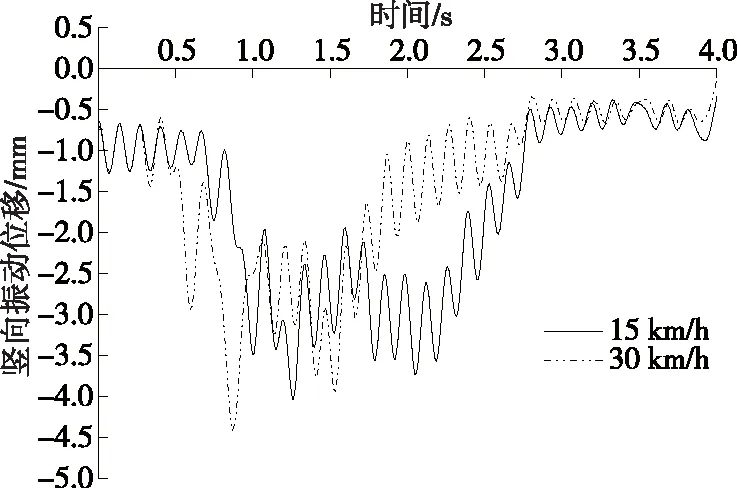
图15 车速对钢栈桥下弦杆跨中节点竖向振动位移的影响

从图14可以看出：车辆行驶速度相同时，车辆质量增大一倍，钢栈桥下弦杆跨中节点竖向最大振动位移增大55.57%，增幅明显。当钢栈桥产生较大变形时，需考虑行车荷载引起钢栈桥疲劳的问题。车辆超载对桥梁结构疲劳损伤的影响更显著。

从图15可以看出：车辆质量相同的情况下，速度增大一倍，钢栈桥下弦杆跨中节点竖向最大振动位移增大4.39%，单从增大幅度来看速度影响较小；短时间内车速越快，钢栈桥振动幅度越大，短时间内振动幅度突然增大会对钢结构桥梁的稳定性产生影响。

3.2.2 振动应变对比

2种工况下钢栈桥下弦杆跨中振动应变对比见图16、图17。

从图16可以看出：车辆行驶速度相同时，车辆质量增大一倍，钢栈桥的振动规律大体一致，跨中最大振动应变增大17.89%。

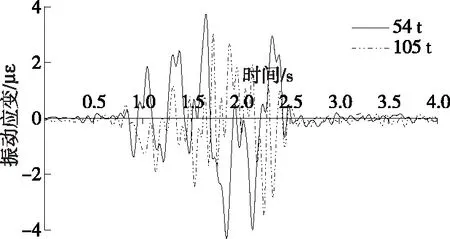
图16 车辆质量对钢栈桥下弦杆跨中动应变的影响

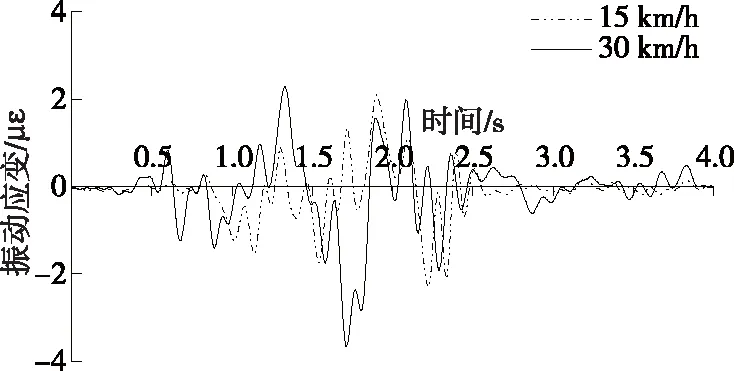
图17 车速对钢栈桥下弦杆跨中动应变的影响

从图17可以看出：车辆质量相同的情况下，车速增大一倍，钢栈桥的振动规律有明显差别，主要体现在最大振动应变及整车完全驶过跨中后对跨中持续影响的能力。车速增大一倍，最大振动应变增大17.01%，在2.5 s后，整车驶过跨中，车速为30 km/h时振动应变仍在小幅变化，说明车速增大会对钢栈桥产生持续的振动影响。

4 结论

本文通过ANSYS建立单跨钢栈桥有限元模型，基于LS-DYNA程序建立显式车-桥耦合振动分析系统，以车辆质量、车辆速度为参数，对比分析各工况下钢栈桥的振动响应，得出以下结论：1) 通过现场静载试验和动载试验结果与有限元数值模拟结果的对比，调整钢栈桥模型弹性模量为设计值的88%使其与实桥更吻合。2) 车辆质量增大一倍，钢栈桥跨中竖向振动位移增大55.57%，竖向动应变增大17.89%。3) 车速增大一倍，钢栈桥跨中最大振动位移增大4.39%，车速越快，振动幅度增大，且对钢栈桥的振动影响时间增长。

本文尚未研究桥面平整度改变时钢栈桥的振动响应，这种情况可作为后续研究方向。