基于5-SPS并联机构的锚杆钻机机构运动学研究*

刘云龙， 罗彪， 黄苛， 罗运杰， 凌涛， 尹来容

(1.中铁五局集团 第一工程有限责任公司， 湖南 长沙 410117；2.长沙理工大学 汽车与机械工程学院， 湖南 长沙 410114)

在当前科学技术高速发展的背景下，岩土工程中锚固技术应用越来越普遍。王鹏设计了一种四臂锚杆钻车，主要应用于魏墙煤矿双巷掘进工作面。王威设计了一种用于完成巷道中全部顶板锚杆支护和侧帮锚杆支护的锚杆钻机，解决了掘锚机组无法一次性完成全部巷道锚杆支护的问题。并联机构具有精度高、累计误差小、承载能力大等特点。Li Y. B.等提出了一种5-PSS/UPU并联机构并对其进行了运动学与动力学求解。柳纪琛等提出了一种两平移一转动(2T1R)并联机构，并对其进行了运动学分析与工作空间及尺度优化。沈惠平等提出了一种零耦合度、含1条冗余支链的三自由度2T1R并联机构,并对该机构进行了运动学与刚度分析。叶伟等提出了一种用于微创手术的新型远中心并联机构，并对该机构进行了运动学分析与性能优化。本文以5-SPS并联机构为研究对象，建立位置反解模型进行锚杆钻机机构运动学求解。

1 机构运动学分析

1.1 机构系统坐标系的建立

如图1所示，在5-SPS直线动平台并联机构的定平台上建立定坐标系O-XYZ(简称O坐标系)，在直线动平台上建立动坐标系P-xyz(简称P坐标系)。定平台上5个铰链点中，第3个铰链点S13位于O坐标系Y轴正方向，其余4个铰链点均匀分布在以坐标系原点为圆心、半径为R的圆上，分布角为72°。直线动平台上第1个铰链点S31至第5个铰链点S35间隔均匀分布在P坐标系x轴负方向，分布值为b/2,第5个铰链点S35与P-xyz坐标系原点的距离为a。

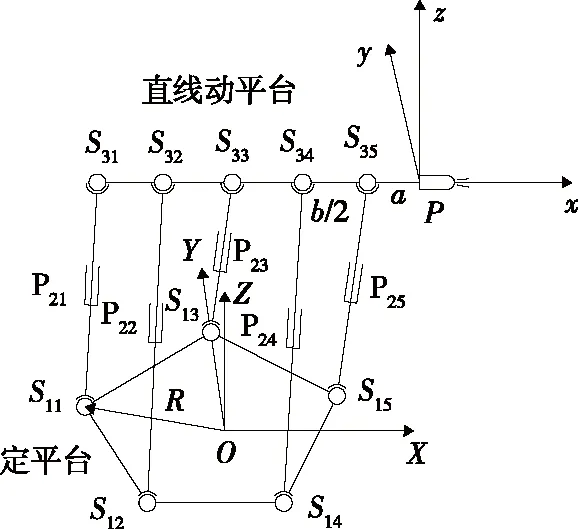
P21～P25代表5个移动副

P坐标系相对于O坐标系的旋转矩阵为：

ORP=R(y,β1)R(z,β2)=

(1)

式中：β1、β2分别为末端输出沿Y方向和Z方向转动的旋转角。

1.2 机构位置分析

该机构的逆解可以简单描述为：已知动平台的空间位置和姿态，即给定动平台末端输出点P的位姿(x，y，z，β1，β2)，求解该机构的输入量，即与定平台相连接的该并联机构5个驱动杆的位移L1、L2、L3、L4、L5。机构各铰链点坐标见表1。

表1 5-SPS并联机构铰链点坐标

OS3i在O坐标系下的坐标为：

OS3i=ORP×PS3i+P

(2)

式中：P为P坐标系的原心相对于O坐标系的坐标表示，即输出，P=[x,y,z]T。

对于该并联机构的5个驱动杆，其杆长矢量为OS1iOS3i(i=1,2,3,4,5)。该并联机构的位置约束方程为：

(i=1,2,3,4,5)

(3)

给定该并联机构结构参数a、b后，根据动平台运动规律，由式(3)可求出该并联机构的位置逆解。

1.3 速度分析

对式(3)两端求导，建立该并联机构的速度方程，其矩阵形式为：

(4)

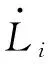
Jε、Jx的形式如下：

式中：

由式(4)可得速度方程为：

(5)

当det(Jε)≠0和det(Jx)≠0时，Jε和Jx均为满秩矩阵，此时Jε和Jx可逆。

(6)

式中：

1.4 加速度分析

对式(3)进行二阶求导，得：

(7)

式中：Hi为该并联机构的二阶影响系数矩阵，为Hessian矩阵，是一个5层5行5列的五维立体矩阵，自上而下共分为5层，其中每个元素均为1×5的矩阵；J为雅克比矩阵。

2 运动学分析算例

取中间分布值b/2为162 mm，a为200 mm，定平台外接圆半径R为340 mm。设定机构动平台初始位置为P=(545，-134，920)T，驱动函数为：

(8)

式中：t为时间变量，其取值范围为0～10 s。

利用MATLAB编程，绘制各驱动副位置、速度及加速度曲线(见图2～4)。

图2 驱动副L1～L5的位移变化曲线

图3 驱动副L1～L5的速度变化曲线

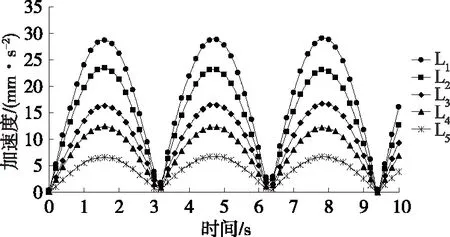
图4 驱动副L1～L5的加速度变化曲线

通过ADAMS软件对该并联机构进行运动学仿真，设定其运动驱动函数为：

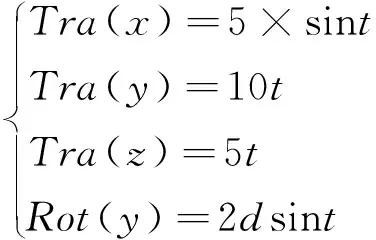
(9)

式中：d为每秒转的角度。

设置仿真时间为10 s，步数为200，在后处理中生成驱动副L1～L5的位置、速度及加速度曲线(见图5～7)。

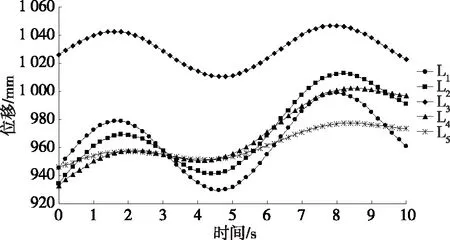
图5 驱动副L1～L5的位移仿真曲线

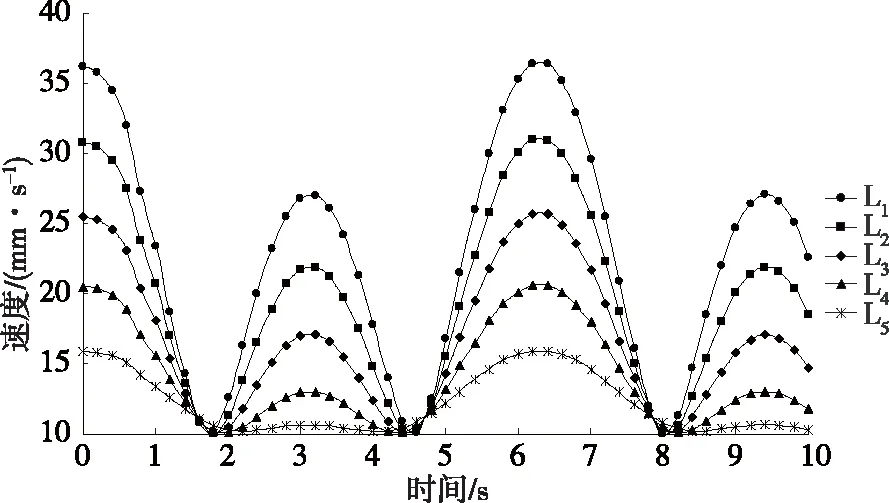
图6 驱动副L1～L5的速度仿真曲线

图7 驱动副L1～L5的加速度仿真曲线

对比图2～4和图5～7，仿真分析结果与理论计算结果一致。根据上述逆向仿真结果，得到该并联机构运动曲线呈有规律的周期性变化，驱动副L1～L5的运动变化平稳，该并联机构具有良好的逆向运动特点。

3 机构奇异性分析

3.1 逆解奇异

矩阵Jε奇异而矩阵Jx非奇异，此时矩阵Jε行列式为零，矩阵Jx行列式不为零，并联机构的自由度增多，驱动机构没有输入，但动平台仍能运动，导致运动失控，此类奇异称为逆解奇异。

求解矩阵Jε行列式为零需满足的条件为L1、L2、L3、L4、L5的乘积为零，即矩阵对角线上的5个元素中至少需满足其中一个为零。当L1、L2、L3、L4、L5中任一个为零时，Jε行列式为零。

对于杆长L1、L2、L3、L4、L5，考虑并联机构的运动特性，由于伸缩杆的长度不可能为零，矩阵Jε和Jx行列式均不为零，不存在逆解奇异。

3.2 正解奇异

矩阵Jx奇异而矩阵Jε非奇异，此时矩阵Jε行列式不为零，矩阵Jx行列式为零，并联机构的自由度减少，机构丧失某种功能，此类奇异称为正解奇异。在MATLAB中编程，得出矩阵Jx的行列式分布(见图8)。

图8 Jx行列式分布

从图8可以看出：Jx的行列式分布并没有一个从零过渡的区间，不存在行列式为零的情况，Jx各行各列都不线性相关，矩阵Jx行列式不为零，并联机构不存在正解奇异。

3.3 混合奇异

矩阵Jε、Jx奇异，此时矩阵Jε和Jx行列式均为零，此为混合奇异。综合以上分析，该并联机构不存在混合奇异。

4 结论

本文利用空间位置矢量法构建5-SPS并联机构的运动学逆解模型，通过ADAMS仿真验证，所设计的理论模型与仿真模型正确、合理，该并联机构动平台加速度变化较平稳，具有较好的运动学性能。求解该并联机构的速度雅可比矩阵，并利用该矩阵对机构奇异性进行分析，结果表明该机构不存在正解奇异、逆解奇异与混合奇异。