含附加能量支路的虚拟同步双馈风机次同步振荡抑制策略

沈雅琦，马 静，李鹏冲，霍乾涛，孙素娟，黄远彦，赵书强

（1. 新能源电力系统国家重点实验室（华北电力大学），北京市 102206；2. 国网漯河供电公司，河南省漯河市 462300；3. 国电南瑞科技股份有限公司，江苏省南京市 211106；4. 北京金风科创风电设备有限公司，北京市 100176）

0 引言

虚拟同步双馈风机具有类似同步发电机的惯性和频率响应特性，可作为未来风机并网的关键技术［1-5］。然而，虚拟同步控制策略的引入使得双馈风机与电网交互特性也发生了质的改变，在双馈风电场经串补线路远距离输电时，可能改变系统次/超同步频段响应特性，影响系统次同步振荡稳定水平，威胁电力系统安全稳定［6-7］。因此，亟须构建适用于虚拟同步双馈风机次同步振荡的阻尼方案，提升系统安全稳定运行能力。

目前，针对次同步振荡的控制策略研究主要围绕传统双馈风机进行设计，从改善风机次/超同步频段上的动态特性出发，包括振荡滤波、参数优化和有源阻尼这3 种方式。振荡滤波主要通过在控制环节中加入带通滤波器，滤除控制环节中所包含的振荡分量，消除次同步频段下的机网耦合作用［8-9］。然而，此类滤波器参数针对某一固定谐振频率点设计，仅适用于单一振荡场景，当电网的运行方式改变时，该控制策略难以自适应振荡频率变化。参数优化主要通过量化风机控制参数与阻尼水平的关联关系，构建控制参数优化模型，提升系统次同步振荡稳定性［10-11］。但受风机正常稳定运行需求的限制，机组变流器控制参数可调整范围有限。有源阻尼是目前最常用的控制策略，其主要通过在转子侧和网侧变流器中附加控制支路或控制环节，优化风机整体阻尼水平［12-13］。然而，现有控制主要针对传统双馈风机进行设计，但虚拟同步双馈风机的控制结构与传统双馈风机之间存在较大差异，对应的控制策略设计思路也有所区别，现有有源阻尼控制策略的适用性仍有待验证。

目前，针对虚拟同步双馈风机振荡稳定性的研究，主要集中于虚拟同步发电机（VSG）控制的电压源型逆变器。文献［14-17］构建了VSG 线性化模型，兼顾系统阻尼和响应特性要求，提出了VSG 参数优化方法；文献［18-20］探究了阻尼系数和系统频率的关联关系，并提出了基于频率偏差的自适应阻尼算法，构建了阻尼系数调节方法。上述研究主要围绕VSG 的低频动态特性进行分析，虚拟同步双馈风机次同步振荡的发生发展诱因尚未阐明，难以从源头实现系统振荡抑制。

针对上述问题，本文提出了一种含多附加能量支路重塑的虚拟同步双馈风机次同步振荡控制策略。首先，根据虚拟同步控制策略划分能量支路，并探究能量支路对能量耗散率的不同贡献程度，筛选关键能量支路。在此基础上，构建附加能量补偿支路，补偿抵消系统中正动态能量，并以系统总能量耗散率最小为目标，设计多能量支路参数优化模型，在兼顾基频稳定需求的基础上，实现次同步振荡抑制。最后，在RT-LAB 仿真平台上进行了试验验证。

1 含虚拟同步的双馈风机动态能量模型

双馈风电场并网结构见附录A 图A1。含虚拟同步控制的双馈风机经0.69 kV/35 kV 变压器接入风电场汇集母线，再经35 kV/500 kV 变压器，通过串补线路连接到无穷大电网。

根据文献［21］，基于节点电流方程，对任意系统的节点电流方程取虚部并积分，可构造一种能量保守系统如式（1）所示。

式中：Y为网络导纳矩阵；UB为各节点电压；IG和IL分别为发电机节点和负荷节点注入电流；“*”表示共轭。

附录A 图A1 所示系统主要包括双馈风机、串补线路和无穷大电网。由于无穷大电网的电压恒定，其电压变化率为0，则无穷大电网能量为0，系统总能量主要由双馈风机能量与串补线路能量构成。结合式（1），该系统能量可写为：

式中：WDFIG为双馈风机产生的动态能量；WLC为串补线路产生的能量；IGi为第i台风机的端口电流；Ui为 第i台 风 机 的 端 口 电 压；Id、Iq和Ud、Uq分 别 为 风机端口电流和电压的d、q轴分量；K为恒定常数；P为双馈风机的有功功率；θ为双馈风机的功角；ωd为转子角速度的d轴分量；C为线路中的串补电容；L为线路中的等效电抗；U为风机端口电压幅值。

由式（2）可知，WDFIG＞0 且满足对所有状态变量均具有连续的一阶偏导数。因此，WDFIG满足李雅普诺夫函数基本性质，本文将其定义为双馈风机的端口动态能量，其振荡过程中的瞬时变化量ΔWDFIG可写为：

式中：Δid、Δiq和Δud、Δuq分别为风机端口电流和电压变化量的d、q轴分量；ΔP为风机端口有功功率变化量；Δθ为风机端口电压相角变化量。

双馈风机主要通过定子侧送出功率，其大小及相角主要受转子侧变流器控制的影响。因此，式（3）中ΔP对Δθ的积分可由转子侧功率ΔPr和转子电压相角变化量Δθr表示。因此，式（3）可写为：

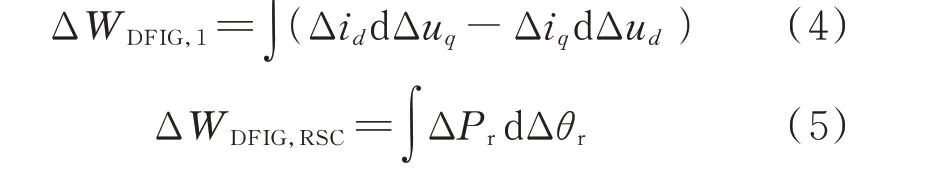
式中：ΔWDFIG，1为受dq轴电流、电压分量影响的能量项；ΔWDFIG，RSC为受转子侧有功功率和电压相角影响的能量项。

分别对这两部分动态能量进行推导。根据文献［22］，可得含虚拟同步控制的双馈风机线性化模型为：

式中：ΔUr为转子电压幅值指令值；Rv为虚拟电阻；Δurd、Δurq和Δird、Δirq分别为转子侧电压和电流d、q轴分量的变化量；Kqp1和Kqi1分别为无功功率控制回路的比例、积分参数；ωb为转速基准值；Δps和Δqs分别为双馈风机定子有功功率和无功功率的变化量；Tj为虚拟惯性时间常数；D为虚拟阻尼系数；Ur0为转子电压稳态幅值。

假设定子磁链恒定，忽略定子电阻的影响，联立双馈风机在同步旋转dq坐标系下的定、转子电压以及磁链方程，可得振荡过程中双馈风机转子电流和电压在dq轴下的变化量为：

式中：Δisd和Δisq分别为定子侧电流d、q轴分量的变化量；Ls和Lr分别为定子、转子等效自感；Lm为定转子互感；ωslip为双馈风机的转差角速度。

将式（8）和式（9）代入式（4），可得ΔWDFIG，1的表达式为：

式中：Δusd和Δusq分别为定子侧电压d、q轴分量的变化量；Rg为双馈风机的定子电阻。

将式（6）和式（7）代入式（5），可得ΔWDFIG，RSC的表达式为：

式中：Us为定子电压幅值；ird0、irq0和urd0、urq0分别为转子电压和电流的d、q轴稳态分量。

由式（10）和式（11）可得含虚拟同步控制的双馈风机动态能量表达式，该模型中受转子侧变流器控制参数影响，可通过评估双馈风机内部各控制参数对系统总动态能量变化趋势的影响，提出相应的振荡抑制措施。

2 含附加能量支路的振荡抑制策略

2.1 控制支路动态能量分析

结合Lyapunov 第二稳定定理，对于一个自由系统，若系统的总能量V(V＞0)随时间的导数恒为负值，则系统总能量不断减少，最终达到最小值，即平衡状态，则此系统稳定［23］。因此，当双馈风机的WDFIG逐渐减少，即动态能量变化率恒为负值时，系统总能量不断减少到最小值，最终系统达到稳定。若WDFIG逐渐增加，其变化率恒为正值，系统总能量不断增多，最终振荡失稳。本文根据Schultz-Gibson的变量梯度法思想，将动态能量ΔWDFIG关于时间的导数定义为能量耗散率aEnergy，根据能量耗散率的符号评估系统稳定水平，其表达式为：

当aEnergy＜0 时，风机产生的能量不断降低，当其降到最低点，系统收敛至稳定。当aEnergy=0 时，风机累积和消耗作用达到相对平衡，产生的动态能量为恒定值，系统处于临界稳定。当aEnergy＞0 时，风机产生的动态能量不断增大，系统逐渐失稳。

在风机动态能量模型的基础上，本文进一步划分系统能量支路，并以降低系统能量耗散率为目标，在控制系统中设计附加能量支路。首先，需要追踪能量在控制系统中的流通路径，划分能量支路，探究各能量支路对能量耗散率的贡献。由附录A 图A1可知，含虚拟同步控制的双馈风机主要包含3 条控制支路：无功功率控制支路、有功功率控制支路以及虚拟电阻控制支路。其中，有功功率控制支路影响的振荡分量为Δθr，无功功率控制支路影响的振荡分量为ΔUr，虚拟电阻控制支路影响的振荡分量为转子电压增量IabcRv，其中Iabc为abc 坐标下转子电流测量值。结合式（6）和式（7）可知，上述3 条控制支路对转子电压和电流dq轴振荡分量产生影响：有功功率控制支路改变Δurq；无功功率控制支路改变Δurd；虚拟电阻控制支路改变Δird和Δirq。进一步，结合动态能量推导过程，按照控制支路中的能流路径，将式（10）和式（11）划分为6 条能量支路，如图1 所示。

图1 动态能量支路Fig.1 Dynamic energy branches

图1 中：ΔWDFIG，1，Q和ΔWDFIG，RSC，Q分别为受无功功率控制支路与定子侧状态量影响的能量支路、受无功功率控制支路与有功功率控制支路影响的能量支 路；ΔWDFIG，1，P和ΔWDFIG，RSC，P分 别 为 受 有 功 功 率控制支路与定子侧状态量影响的能量支路、受有功功 率 控 制 支 路 影 响 的 能 量 支 路；ΔWDFIG，1，ii和ΔWDFIG，RSC，ii分 别 为 虚 拟 电 阻 控 制 支 路 与 定 子 侧 状态量共同决定的动态能量、受虚拟电阻控制支路与有功功率控制支路影响的能量支路。

将式（10）和式（11）代入式（12），推导各能量支路对应的能量耗散率，并对其进行解析，探究各能量支路对系统总能量耗散率的贡献，筛选影响系统次同步振荡稳定性的关键能量支路，并据此设计附加能量支路。

受无功功率控制支路与定子侧状态量影响的能量支路为ΔWDFIG，1，Q，其能量耗散率aDFIG，1，Q可写为：

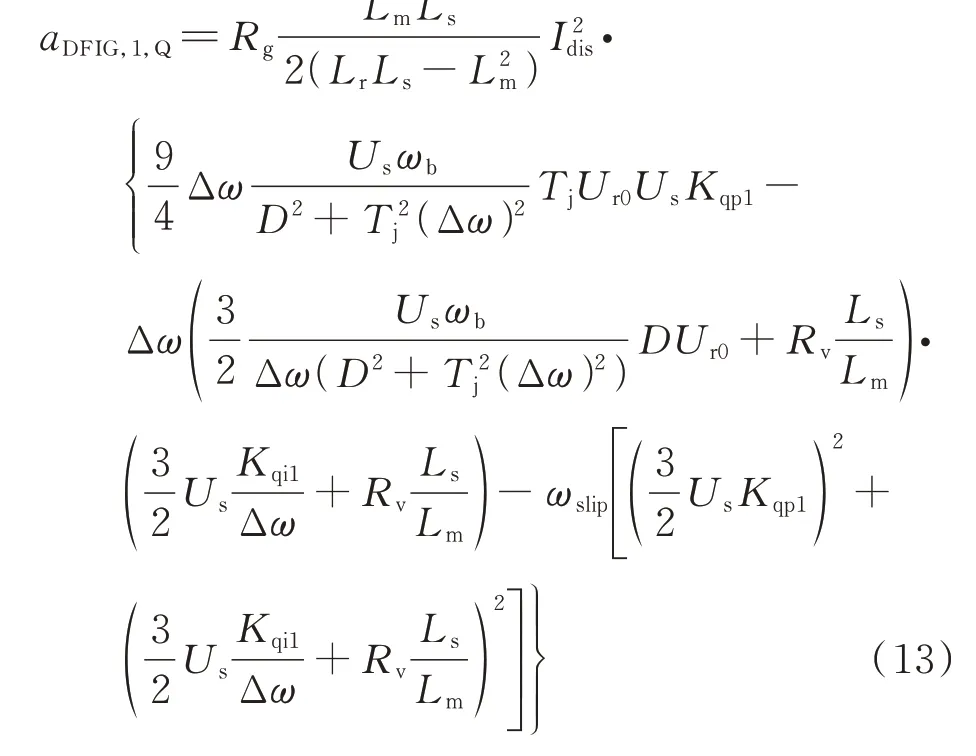
式中：Idis为扰动电流的幅值；Δω=ωs-ωdis，其中，ωs为工频转子角速度，ωdis为次同步扰动下的转子角速度。风机处于发电状态时，双馈风机的转差角速度ωslip＜0，对应的Δω和-ωslip所在项也为正值，即这两项可能助增系统能量耗散率；-Δω所在项为负值，有利于降低能量耗散率。因此，ΔWDFIG，1，Q可正可负。

受无功功率控制支路与有功功率控制支路影响的能量支路为ΔWDFIG，RSC，Q，其能量耗散率aDFIG，RSC，Q可写为：

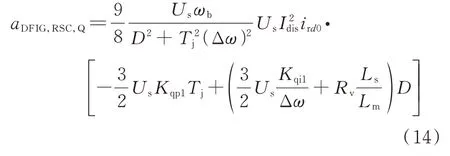
由式（14）可以看出，Kqp1所在项为负值，产生负能量耗散作用；Kqi1和Rv所在项均为正值，助增系统能量耗散率。因此，ΔWDFIG，RSC，Q中产生的耗散作用可正可负。

受有功功率控制支路与定子侧状态量影响的能量支路为ΔWDFIG，1，P，其能量耗散率aDFIG，1，P可写为：

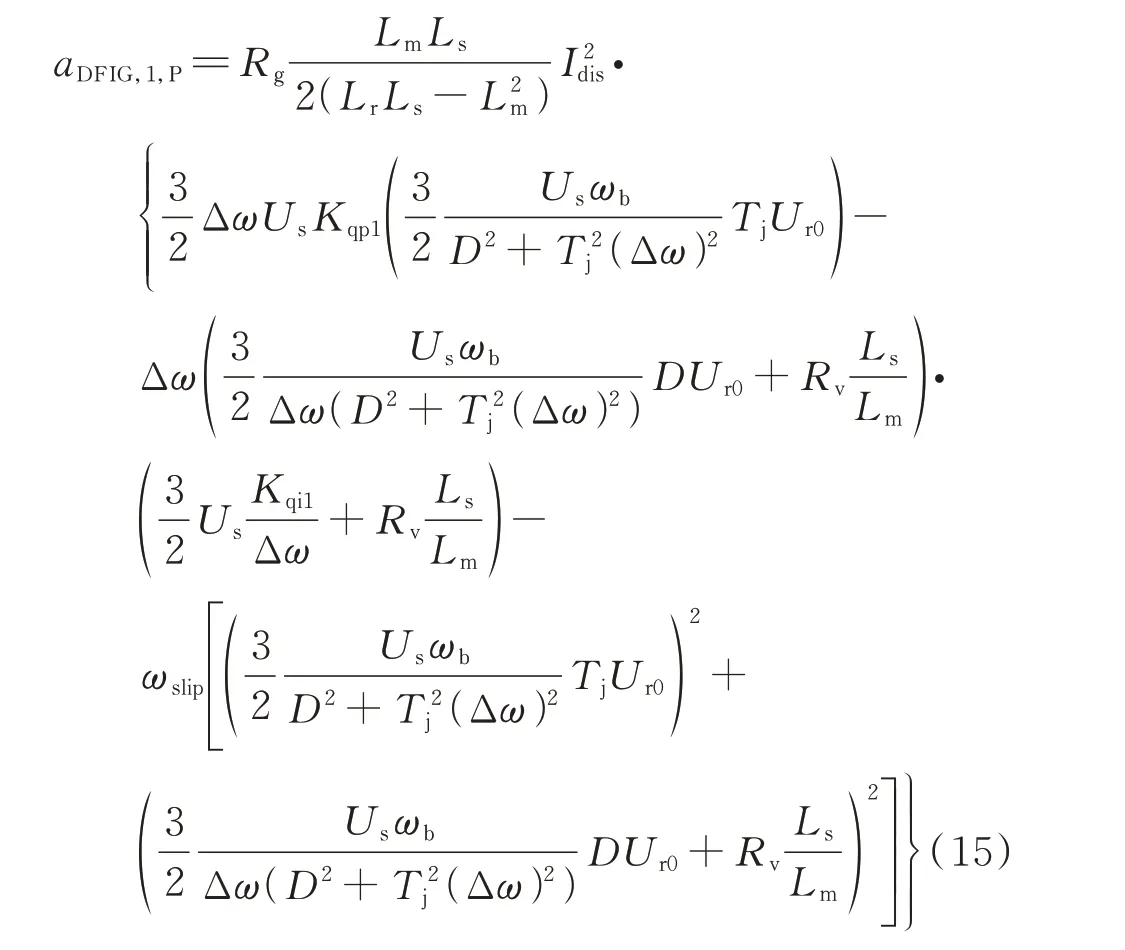
由式（15）可知，Δω和-ωslip所在项为正值，可能增大系统能量耗散率；-Δω所在项为负值，产生负能量耗散作用。因此，ΔWDFIG，1，P产生的能量耗散作用可正可负。

仅受有功功率控制支路影响的能量支路为ΔWDFIG，RSC，P，其能量耗散率aDFIG，RSC，P可写为：

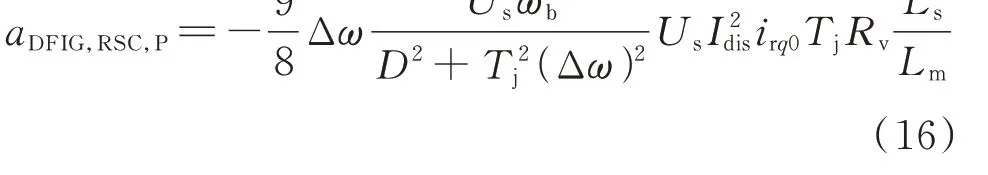
由式（16）可知，ΔWDFIG，RSC，P中仅存在负动态能量，有助于降低系统能量耗散率。

虚拟电阻控制支路与定子侧状态量共同决定的动 态 能 量 为ΔWDFIG，1，ii，其 能 量 耗 散 率aDFIG，1，ii可写为：

由式（17）可知，aDFIG，1，ii恒为正值，可能助增系统 能 量 耗 散 率。相 应 地，ΔWDFIG，1，ii只 存 在 正 动 态能量。受虚拟电阻控制支路与有功功率控制支路影响的 能 量 支 路 为ΔWDFIG，RSC，ii，其 能 量 耗 散 率aDFIG，RSC，ii可写为：

由式（18）可知，aDFIG，RSC，ii恒为正值，助增系统能量 耗 散 率，相 对 应 地，ΔWDFIG，RSC，ii只 包 含 正 动 态能量。

综合上述分析，ΔWDFIG，RSC，ii和ΔWDFIG，RSC，P所在能量支路与其他支路呈现弱耦合，其中，ΔWDFIG，RSC，ii可能助增系统能量耗散率，ΔWDFIG，RSC，P有助于降低能量耗散率。

此 外，由 式（13）和 式（15）可 知，ΔWDFIG，1，Q和ΔWDFIG，1，P的 能 量 耗 散 率 较 为 接 近，即aDFIG，1，Q≈aDFIG，1，P。而式（16）中，Δωωb为次同步角速度与同步角速度的差值，数量级一般为102，因此aDFIG，RSC，P的数值远大于aDFIG，1，P和aDFIG，1，Q，即受无功功率控制支路影响的能量支路对振荡的贡献较小。此外，ΔWDFIG，1，Q和ΔWDFIG，1，P同 时 还 与 其 他 支 路 相 互 耦合，难以解耦。因此，不宜在该支路中设计补偿环节，而虚拟电阻控制支路和有功功率控制支路与其他支路耦合较弱，且对能量耗散率贡献较大，可通过对其进行能量补偿，提升系统稳定性。

2.2 附加能量控制支路构建

本文以降低系统动态能量、减小能量耗散率为目标，构建能量补偿支路。基于2.1 节中各控制支路 能 量 耗 散 率 的 分 析，本 文 结 合ΔWDFIG，1，ii和ΔWDFIG，RSC，P的构成形式，在虚拟电阻控制支路和有功功率控制支路设计能量补偿支路。

1）虚拟电阻控制支路

由图1 可知，ΔWDFIG，1，ii与其他控制支路不存在耦合关系，可根据ΔWDFIG，1，ii的流通路径及构成方式构建附加能量支路1。

由式（17）可知，能量耗散率aDFIG，1，ii主要受Δurd和Δurq幅值系数影响，其中，针对系数A2、A4，可针对虚拟电阻控制支路产生的正动态能量，设计反向补偿能量，降低其幅值系数，从而降低aDFIG，1，ii，补偿支路如图2 蓝色框图所示。引入补偿支路后的虚拟电阻控制支路表达式为：

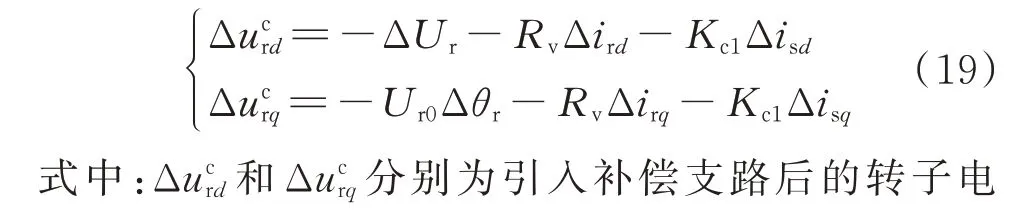
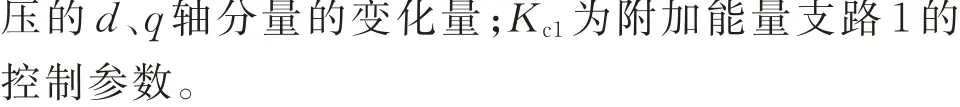
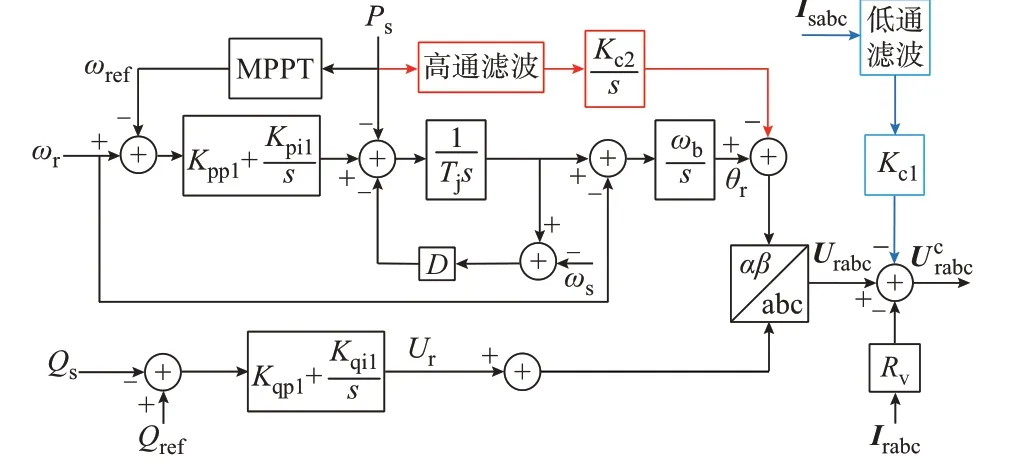
图2 含附加能量支路的控制策略Fig.2 Control strategy with additional energy branch

将式（19）代入式（11）后可推导得到附加能量支路1 后 的 动 态 能 量ΔWDFIG，1，ii的 表 达 式，并 结 合 式（14）得到能量耗散率a'DFIG，1，ii为：

对比式（20）与式（17）可知，在引入附加能量支路 后，ΔWDFIG，1，ii的 能 量 耗 散 率 下 降，系 统 稳 定 性提升。

进一步，考虑到附加支路可能会影响其他能量支路的稳定性，需要对其他能量支路进行校验。结合图1 可知，引入附加能量支路1 后，ΔWDFIG，RSC，ii中出现新增能量分量，其能量耗散率的变化量ΔaDFIG，RSC，ii为：

根据式（21）可知，附加能量支路1 在ΔWDFIG，RSC，ii中引入负动态能量，有助于降低能量耗散率，提升系统稳定性。

2）有功功率控制支路

由2.1 节 分 析 可 知，ΔWDFIG，RSC，P与 其 他 控 制 支路相互解耦，可根据ΔWDFIG，RSC，P的构成路径设计附加能量支路2。

由 式（16）可 知，ΔWDFIG，RSC，P会 产 生 负 动 态 能量，可在有功功率控制支路中设计附加能量支路2，降低该支路产生的能量耗散率，增大其产生的负动态能量。附加能量支路如图2 红色框图所示。引入附加能量支路2 后，有功功率控制支路可写为：

由式（23）可知，引入附加能量支路2 后，ΔWDFIG，RSC，P中产生了负动态能量增量，有助于降低能量耗散率，减少动态能量累积。

进一步，考虑两条附加能量支路引入后可能影响其他控制支路的稳定性，需要对其进行校验。当投入两条附加能量支路时，ΔWDFIG，1，P中出现新增能量 分 量，对 应 的 能 量 耗 散 率 变 化 量 为ΔaDFIG，1，P，可写为：

由式（24）可知，ΔaDFIG，1，P由附加能量支路的控制参数Kc1和Kc2共同决定，需要对该参数进行合理配置，保证ΔWDFIG，1，P产生负能量耗散率，引入正耗散作用，提升系统稳定水平。

引入两条附加能量支路后，ΔWDFIG，1，Q中产生的新增能量耗散率可写为：

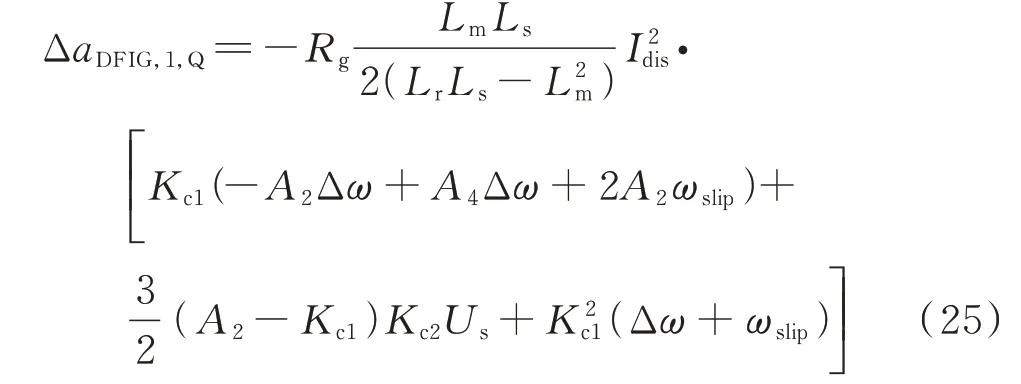
由式（25）可知，ΔWDFIG，1，Q的正负受Kc1和Kc2影响，需要对这两个控制参数进行合理配置，才能在ΔWDFIG，1，Q中引入负的能量耗散率，提高系统稳定性水平。

引入两条附加能量支路后，ΔWDFIG，RSC，Q中出现新的能量分量，对应的ΔaDFIG，RSC，Q可表达为：

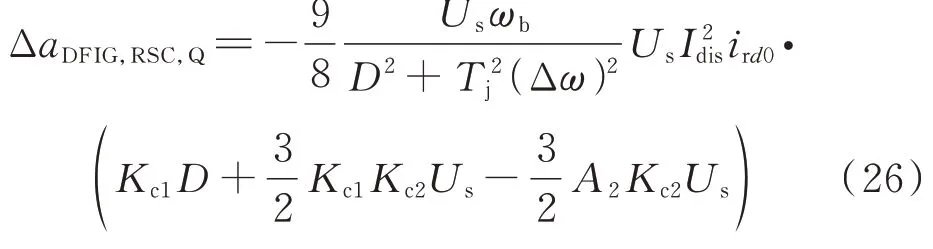
由 式（26）可 知，ΔWDFIG，RSC，Q的 正 负 性 同 样 由Kc1和Kc2共同决定，需要对这两个参数进行合理设定，才能保证ΔWDFIG，RSC，Q产生负能量耗散率。

引入两条附加能量支路后的控制框图如图2 所示。图中：Irabc、Urabc和Isabc分别为转子侧三相电流、三相电压和定子侧三相电流；Ucrabc为引入控制支路后的转子侧三相电压；Ps和Qs分别为双馈风机定子输出的有功和无功功率；Qref为无功功率的参考值；ωr为双馈风机转子角速度；ωref为以最大风电功率追踪所计算的转子角速度参考值；θr为转子电压相角；Kpp1和Kpi1分别为有功功率控制回路的比例、积分参数；MPPT 表示最大功率点跟踪控制。

引入附加能量支路后，有功功率支路控制方程为：

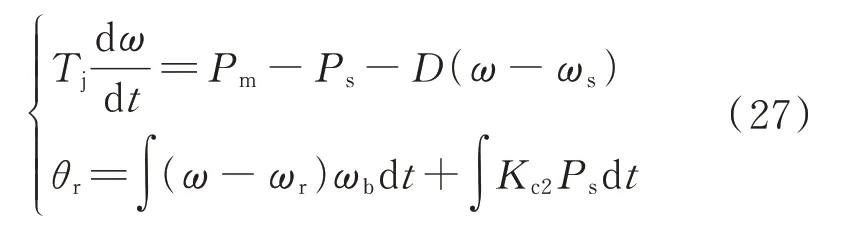
式中：Pm为双馈风机等效机械功率；ω为双馈风机虚拟定子角速度。

由式（27）可知，附加能量支路1 的引入会导致转子电压变化，若该支路参数设置过大，转子电压变化量也会随之增大，从而改变双馈风机的基频响应。因此，需要配置低通滤波器滤除基波频率，保证仅次同步分量通过，对转子电压中的振荡分量进行补偿，减小补偿支路对稳定工况下风机正常运行能力的影响，保证了风机在基频下的稳定性，滤波器的位置如图2 蓝色控制支路所示。此外，引入附加能量支路2 会导致转子电压相角变化，进而改变风机的频率响应。为兼顾风机调频需求，本文设置高通滤波器滤除基频分量，仅保证次同步振荡分量进入控制支路，滤波器的位置如图2 红色控制支路所示。

综上所述，针对虚拟电阻控制支路和有功功率控制支路设计的附加能量支路1 和2 能够在风机中引入负能量耗散率，降低风机产生的动态能量。但是引入附加能量支路1 可能导致稳态转子电压变化，影响风机的正常稳定运行，其产生的次同步频段补偿作用也受到限制。此外，附加能量支路2 在ΔWDFIG，1，P、ΔWDFIG，1，Q和ΔWDFIG，RSC，Q中 引 入 的 能 量增量由控制参数Kc1和Kc2共同决定，如果参数设计不合理，其产生的补偿作用将会减弱，也可能加剧系统振荡发散。因此，需要兼顾次同步频段补偿作用和风机基频特性稳定需求，协同多补偿支路最大程度挖掘附加能量支路对系统次同步频段的补偿作用。

3 附加能量支路控制参数优化

由第2 章分析可知，附加能量支路的参数会影响风机对次同步振荡的阻尼作用以及风机的稳态运行能力，因此，需要对参数进行合理设置。本文在能量耗散率模型的基础上，以系统能量耗散率最小为目标，构建多能量支路参数优化模型，提高振荡稳定水平。

首先，设置目标函数。以系统能量耗散率最小为目标，其表达式为：

式中：ΔaEnergy，l为第l条能量支路的能量耗散率变化量，可由式（20）—式（26）求得；n为能量支路总数。

由式（28）可知，a'Energy受ωs、ωr和ωdis的影响，其中，控制参数Kc1和Kc2为优化对象。

由式（19）可知，附加能量支路会影响风机稳态运行能力。为兼顾风机基频特性稳定需求，需对转子电压设置约束。同时，考虑到补偿支路会通过转子侧换流器改变风机直流母线电压大小，为保证风机的稳定运行，需要兼顾直流母线电压约束，使其变化量小于5%，尽可能降低附加能量支路对风机稳定运行能力的影响。因此，兼顾上述两者要求，设置如下约束条件：

式 中：Ur为 转 子 电 压，Ur，max和Ur，min分 别 为 其 上、下限；Ud为直流母线电压，Ud，max和Ud，min分别为其 上、下限。

其次，为避免出现超调现象引发控制系统失稳，控制参数需要满足控制系统稳定约束。另外，考虑到双馈风机并网系统次同步振荡的振荡频率覆盖范围为5～45 Hz，ωdis需要设置在次同步频段范围内。

在优化过程中，为了加快计算速度，本文设置目标函数约束，即投入附加能量支路后的能量变化率均为负值，保证优化后系统动态能量呈现下降趋势。综合上述分析，多支路控制参数优化模型可表示为：

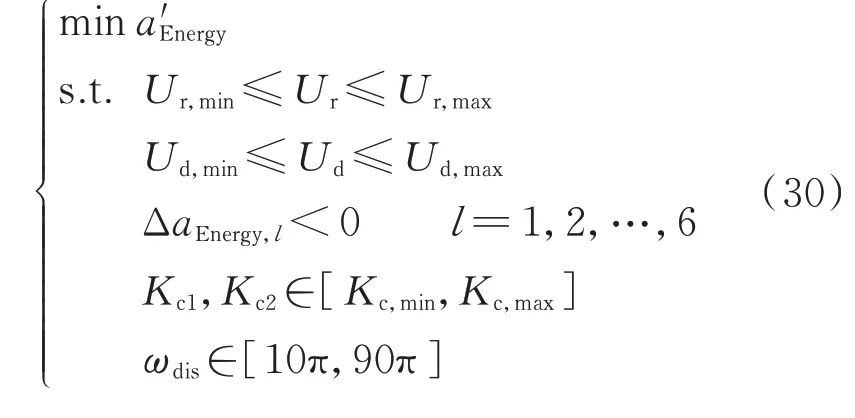
式 中：Kc，max和Kc，min分 别 为 补 偿 支 路 控 制 参 数 的 上、下限。

针对上述优化模型，本文利用细菌群体趋药性算法［24］进行求解，该优化算法的主要步骤如下：

步骤1：初始化各个细菌的位置。将系统控制参数以及状态量代入式（20）、式（21）、式（23）—式（26），计算能量耗散率变化量，并根据式（30）的约束条件描绘控制参数Kc1和Kc2的可行域。

步骤2：设置初始收敛精度ε=0.136 和进化精度更新常数α=1.24。

步骤7：重复步骤3 至步骤6，直至满足终止条件。

基于上述模型，搜索得到最优解Kc1，min和Kc2，min，并将其应用到附加能量支路中，实现多能量支路的协同优化控制。

4 仿真验证

为了验证本文分析结果的真实性，本文根据附录A 图A1 所示网络结构，在RT-LAB 平台搭建仿真模型，试验平台见图A2，风机参数见表A1。

本文首先通过测量风机端口状态量以及本文所推导的各部分能量表达式，计算各部分能量的能量耗散率，验证本文所提各部分动态能量对系统稳定性影响的分析结果。然后，在控制系统中添加附加能量支路的振荡抑制措施，验证本文所提次同步振荡抑制措施的控制效果。

4.1 控制支路动态能量分析验证

当系统受扰激发发散型振荡时，将系统参数代入式（13）—式（18）中，计算6 条能量支路及其耗散率，如图3 所示。

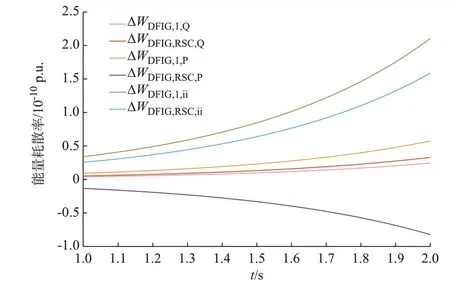
图3 各能量支路的能量耗散率Fig.3 Energy dissipation rate of each energy branch

由图3 可知，ΔWDFIG，1，ii和ΔWDFIG，RSC，ii产生的能量耗散率恒为正值，ΔWDFIG，RSC，P产生的能量耗散率恒为负值，虽然ΔWDFIG，1，Q、ΔWDFIG，RSC，Q、ΔWDFIG，1，P均大于0，但其数值远小于其他控制支路。在2 s 时，ΔWDFIG，1，Q和ΔWDFIG，RSC，Q产生的能量耗散率分别为2.45×10-11和 3.29×10-11； ΔWDFIG，1，P和ΔWDFIG，RSC，P产生的能量耗散率分别为5.74×10-11和-8.27×10-11；ΔWDFIG，1，ii和ΔWDFIG，RSC，ii产生的能量耗散率分别为2.10×10-10和1.59×10-10。根据能量耗散率数值可知，ΔWDFIG，1，Q和ΔWDFIG，RSC，Q对系统阻尼贡献相对较小，并非影响系统稳定性的主要支路。

4.2 附加能量支路振荡抑制效果验证

首先，验证引入两条附加控制支路后对系统振荡的抑制效果。其次，对比验证参数优化后的系统振荡抑制效果。

1）附加能量支路1

在1 s 时投入串补线路，系统激发次同步振荡；在2 s 时投入附加能量支路1，设置该支路控制参数Kc1=0.09。

风机有功功率的变化情况如图4（a）所示。由图可知，2 s 投入附加能量支路1 后，系统由逐渐发散转为收敛，最终收敛至稳定。对风机端口电流进行快速傅里叶变换（FFT）分析，如附录A 图A3 所示，附加能量支路1 投入前，系统激发了14 Hz 左右的次同步振荡和86 Hz 的超同步振荡。投入附加能量支路后，电流中的振荡分量明显降低。

转子侧d轴电压变化曲线如图4（b）所示。由图可知，虽然投入附加能量支路1 后系统振荡逐渐收敛，但转子侧d轴电压的稳态值产生了较大改变，在支路投入前urd0=-0.221 p.u.，支路投入后urd0=-0.175 p.u.，变化量高达20.81%，超出了转子电压允许的变化范围。因此，引入附加能量支路1 在一定程度上能够通过降低风机产生的动态能量抑制系统次同步振荡，但其对风机稳定运行特性会产生负面影响，若该支路参数设置过大，可能恶化风机稳定运行特性。

图4 加入附加能量支路后的双馈风机仿真曲线Fig.4 Simulation curves of DFIG-based wind turbines with additional energy branches

2）附加能量支路2

1 s 时接入串补线路，系统激发发散型振荡，2 s时接入附加能量支路2，其中Kc2=10。为验证该能量支路的阻尼作用，本文分别设置20%和40%串补度下的振荡场景，仿真结果如图4（c）和4（d）所示。由图4（c）可知，当串补度设置为20%时，引入附加能量支路2 后系统振荡快速收敛。但当串补度达到40%时，由图4（d）可知，未投入附加能量支路时系统振荡发散剧烈，投入补偿支路后，系统振荡发散趋势下降，但未达到稳定状态，而是呈现等幅振荡。因此，对比图4（c）和（d）可知，附加能量支路2在一定程度上可以抑制系统振荡，但抑制效果低于附加能量支路1。

综合上述分析，单独投入两条能量附加支路难以兼顾基频特性，实现振荡的有效抑制，需协同多能量支路，尽可能挖掘补偿支路阻尼作用，使得系统总体能量耗散作用达到最优。

3）附加能量支路控制参数优化

同样，1 s 时接入串补线路，系统激发发散型振荡，2 s 时投入两条附加能量支路。为提升附加支路的阻尼作用，利用式（30）的优化模型，以风机总能量耗散率最优为目标，构建优化方案。参数优化结果为：Kc1，min=0.074、Kc2，min=9.69。为对比最优参数和非最优参数下的计算结果，控制参数下的风机能量耗散率的变化情况如图5 所示。由图5 可知，能量耗 散 率 极 小 值a'Energy，min对 应 的 坐 标 为(0.074，9.69，-7.328×10-10)。进一步，分别设置最优控制参数Kc1=0.074、Kc2=9.69 和非最优控制参数Kc1=0.065、Kc2=8.50，进行时域仿真对比，验证参数优化后的振荡抑制效果。

图5 不同参数下的能量耗散率变化情况Fig.5 Variation of energy dissipation rate with different parameters

在1 s 时接入串补线路，系统激发发散型振荡。图6（a）所示为不同附加支路控制参数下的风机动态能量变化曲线。在附加能量支路投入前，风机产生的动态能量不断增长，且速率加快。2 s 后投入附加能量支路，风机产生的动态能量变化逐渐放缓，最终达到恒定值，此时单位时间内风机不再发出动态能量，系统达到稳定。对比最优控制参数和非最优控制参数下的能量变化曲线可知，选取最优控制参数时，动态能量达到稳定状态的速度更快。

图6（b）所示为不同参数下风机能量耗散率的变化情况，在1～2 s 期间，风机能量耗散率恒大于0，且不断增长。在2 s 时引入附加能量支路后，系统能量耗散率由正值转为负值，系统呈现正耗散作用。对比两组控制参数下的能量变化率可知，当采用最优控制参数时，能量变化率的绝对值最大，即能量耗散速度最快，系统稳定性最高。

为验证上述能量分析的准确性，分别针对附加支 路 选 取Kc1=0.065、Kc2=8.50 和Kc1，min=0.074、Kc2，min=9.69 两组参数进行仿真验证。图6（c）所示为不同参数下风机输出的有功功率变化曲线，投入附加支路前，系统呈现发散型振荡；投入附加控制支路后，系统振荡逐渐衰减至稳定。当附加支路参数Kc1，min=0.074、Kc2，min=9.69 时，振 荡 收 敛 速 度 最快，0.6 s 左右达到稳定状态。图6（d）所示为不同参数下风机转子侧d轴电压的变化趋势。投入附加支路后，电压中的振荡分量逐渐收敛，且当选取最优控制参数时，振荡分量收敛速度最快。此外，计算1～2 s 及2 s 以后的转子侧d轴电压稳态值urd0可知，投入控制策略前后差值远小于5%，即该控制策略几乎不影响风机的稳态运行。因此，本文所提的控制策略能够在兼顾工频电压稳定需求的基础上，实现次同步振荡的有效抑制。

图6 不同参数下风机动态能量、能量耗散率及仿真结果Fig.6 Dynamic energy, energy dissipation rate and simulation results of DFIG-based wind turbines with different parameters

5 结语

本文基于动态能量在虚拟同步双馈风机控制支路中的流通路径，划分控制系统中的能量支路，并筛选影响系统次同步振荡稳定性的关键控制支路，在此基础上，以系统能量耗散率最小为目标，构建了基于多能量支路协同优化的次同步振荡抑制策略，主要结论如下：

1）风机各控制回路产生的动态能量之间存在强耦合作用。其中，虚拟电阻控制支路会产生正能量耗散率，助增系统累积动态能量，不利于系统稳定。有功功率控制支路会产生负能量耗散率，降低系统能量累积，有助于提升系统的稳定性。

2）在虚拟电阻控制支路中引入负耗散支路补偿，抵消该支路产生的正耗散作用；在有功功率控制支路中构建负能量耗散补偿支路，可增加风机产生的负动态能量，有助于降低系统能量耗散率，提升系统稳定性水平。

3）考虑到附加能量支路可能影响风机基频特性以及其他能量支路稳定性，以附加能量支路控制参数为优化对象，计及风机基频运行需求约束，以总能量耗散率最优为目标，构建了多能量支路协同优化策略，在兼顾风机基频稳定运行需求的基础上，实现了次同步振荡抑制。

本文控制策略主要基于风电场单机等值并网系统，针对风电场多机间振荡机理及控制策略设计将是下一步的研究工作，本文提供的基于动态能量的风电场级主动阻尼控制初步研究思路，可供读者探讨。在单机建模的基础上，构建风电场级机间交互动态能量模型，追踪能量在多机控制环节间的交互路径，筛选关键交互能量支路。进一步，在关键交互能量支路中，设计能量补偿环节，并以风电场级能量耗散率最小为目标，构建风电场级多机能量协同优化方案，实现多机并网系统次同步振荡抑制。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。