浅谈独立支路法求混联电阻电路的等效电阻

徐礼长

(共青科技职业学院，江西 共青城 330300)

一、引言

在直流电阻电路的分析中，对单一的电阻串/并联电路分析是比较容易解决的问题，但这种单纯的串/并联电路一般较少出现，而大部分电阻电路总是以“混联”的形式出现较多。对于这类电路的分析，一般的求解步骤是先按逐步等效法将电路整理出有规则的，联接关系明确的等效电路，然后再根据电阻的串/并联的特性关系，求出等效电阻和各个支路电流及各段电压。在这个问题上，对于等效电阻的求解方法成为了分析该类电路的根本。它也是研究电路输入输出阻抗及匹配、戴维南定理、诺顿定理等重要课题中求解“等效电阻”必不可少的内容。本文结合多年的教学经验对一些设计巧妙和结构复杂的直流电阻网络进行剖析，介绍一种巧妙的求解方法----独立支路法。

二、独立支路法

1、定义

独立支路是指不重复经过同一电阻而能使电流从正极流回负极的支路。

2、作独立支路的方法

在不剩余无阻导线的前提下让支路包含尽可能多的电阻，而使独立支路数量少，未包含在独立支路中的剩余电阻，由其两端在原电路中的位置决定其在新电路中的关系。

3、一般步骤

①先在原电路图中，给每一个连接点标上字母。

②从待求的等效端口处出发假设一点为起点，分别沿各条独立支路(按作独立支路的方法)绕到端口的另一点(终点)画出独立支路。

③未包含在独立支路中的电阻根据其在原电路中的位置添加到新电路中的对应连接点之间。

④根据整理出来的等效电路求出其等效电阻。

三、案例分析

案例一：如图1-a所示，已知R1=6Ω，R2=R3=10Ω，R4=5Ω，R5=40Ω，R6=15Ω，R7=12Ω，求AB端口处的等效电阻RAB。

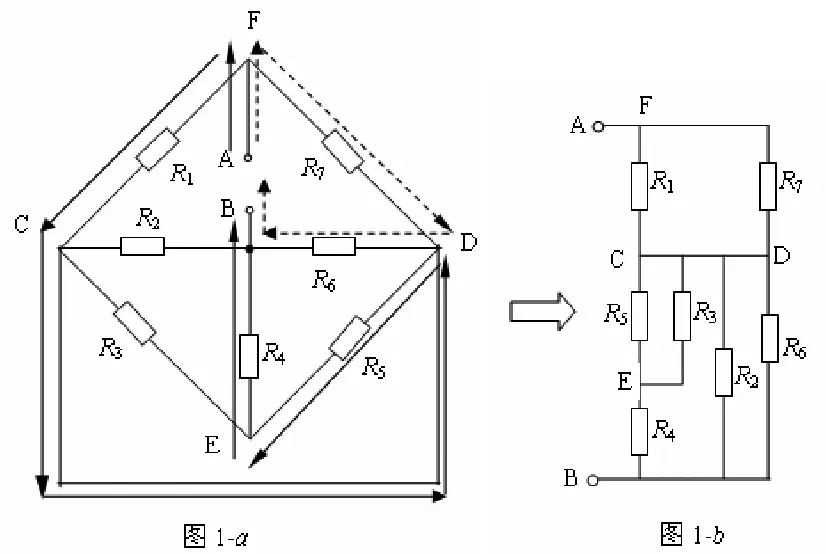
图1 案例一分析：(1)按上述电路分析方法及步骤首先在原图1-a中找到第一条最长的独立支路AFCDEB(如图a实线箭头所示)画于图1-b中。

(2)然后再在原图1-a中找到第二条独立支路AFDB(如图1-a虚线箭头所示)联接在图1-b的对应交点之间。

(3)最后剩余的R2R3应根据其在原电路中的位置确定它在新电路中的关系。于是得到了图1-b所示的完整的，规则的电路图。显然，根据图1-b可确定：

RAB=R1//R7+(R5//R3+R4)//R2//R6=8Ω

本题如果用常规等效法视乎有些繁琐，特别对初学者很难搞定。

案例二：如图2-a所示电路，已知R1=20Ω，R2=40Ω，R3=10Ω，R4=20Ω，R5=40Ω，R6=20Ω，求ab端口处的等效电阻Rab。

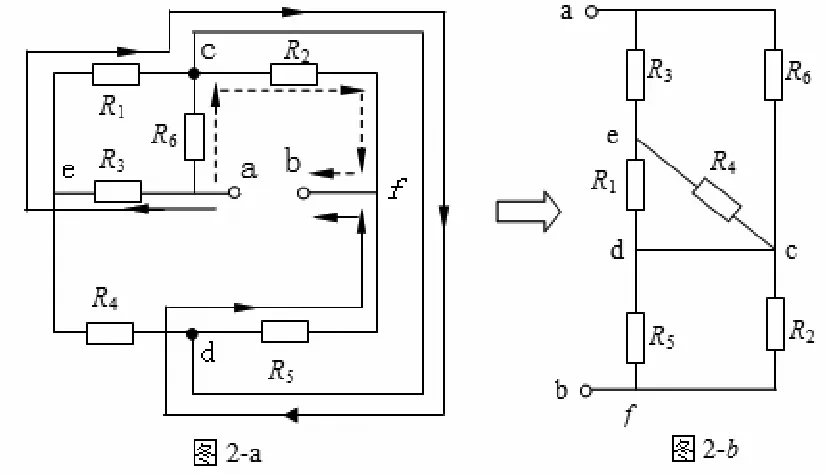
图2 案例二

分析：(1)按上述电路分析方法及步骤首先找到原图2-a所示电路中aecdfb为第一条独立支路，画于图2-b中。

(2)然后找到另一条独立支路acfb画于图2-b中对应的交点之间。

(3)最后剩下的R4根据其在原电路中的位置确定它在新电路中的关系。因此不难算出等效电阻为：

Rab=(R1//R4+R3)//R6+R5//R2=30Ω

四、注意事项

通过以上两个例子读者应该对独立支路法的分析过程有所了解了，但还应注意以下几点：

①在选择独立支路时应使独立支路包含尽可能多的电阻。独立支路越长，电路越好整理。

②当某些电阻的两端跨接短路线时，这个电阻在新电路中无效，自动消失且把这两端视为同一个连接点处理。

③当某些电阻支路开路时，这条支路在新电路中不应出现。

④未包含在独立支路中的电阻应在画完所有独立支路后添加到新电路中去。