基于改进狼群算法的焊接机器人路径规划*

龚 正，涂福泉，李圣伟

(武汉科技大学 机械自动化学院，湖北 武汉 430081)

0 引 言

随着科学技术的发展，焊接机器人在汽车制造业中的作用越来越大，以焊接机器人为核心的生产和技术改革，成为越来越多的学者研究对象，其中研究重点之一就是白车身焊接任务的合理规划[1]。白车身是汽车设计的重要组成部分，拥有着5 000～7 000个焊接点[2]。如果能有效合理的规划出焊接路径，不仅能大大提高焊接机器人的工作效率，也可以降低生产中的成本[3]。焊接路径规划所用方法可以分为两种，传统算法路径规划和智能算法路径规划。传统算法计算速度快，方法也简单，但在解决多焊点离散型问题上很难找到最优解，已不能满足路径规划需求。因此，越来越多的学者开始利用智能算法开展路径规划研究。王春华等人[4]在蚁群算法中加入局部搜索策略，并引入最大最小蚂蚁机制对算法进行了改进，避免算法陷入局部最优，但算法选取精英蚂蚁比较困难，且对路径规划结果影响很大。吴明辉等人[5]提出了一种梯度下降和蚁群的混合算法，通过算法间的结合，增加了蚁群算法在寻优过程中的随机性，但是算法路径规划所用时间太长，不利于提高工作效率。林巨广等人[6]利用蚁群算法对焊接路径进行规划，通过引入评价函数来提升算法的工作效率，但是选取的焊点实在太少，初始路径也比较有规律，不具备普适性。

与上述方法相比，狼群算法(wolf pack algorithm,WPA)具有良好的收敛性和鲁棒性，能够适用于不同的焊接路径，所以选用了WPA对焊接路径进行规划。但WPA也存在着精度不高、容易陷入局部最优且搜索时间太长的不足[7,8]，为此，对WPA进行了改进，提出了一种基于Logistic混沌初始化的模拟退火WPA。将改进WPA应用于TSP和焊接路径规划任务中，利用MATLAB仿真分析验证算法的有效性和可行性。

1 焊接路径规划任务描述

1.1 车门焊接件结构描述

汽车车门是白车身的重要组成部分，车门上焊点分布特征明显，几乎在一个平面上，本文选取上汽荣威IR31白车身车门为示例，忽略焊点高度差，建立二维车门焊接任务模型。如图1(a)为车门结构，从图中可以明显的看出，车门上的焊点数量众多且排列没有规则，现从其中提取出焊点模型，为焊接路径规划做准备。车门焊点模型如图1(b)。

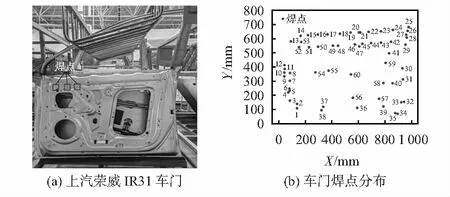
图1 车门模型

1.2 焊接任务描述

本文将焊接总路径距离最短作为目标函数，来进行焊接任务路径规划，即焊接机器人从初始位置出发，在遍历所有焊点后回到初始位置，寻找出一条焊接路径总距离最短的路线。焊接路径规划模型如下：

给定N个焊点，N个焊点的其集合为C=(c1,c2,…,cn)以及各焊点之间的距离d，目标函数为

(1)

式中L为遍历焊点的总路径长度，d(ci，ci+1)为第i个焊点ci与第i+1个焊点ci+1之间的距离，i=1，2，…，n-1，d(cn，c1)为第n个焊点cn到第一个焊点c1之间的距离。在整个路径规划过程中,怎样使目标函数L最小，是路径规划的关键。

2 改进WPA

2.1 WPA

狼群在捕猎过程中分工明确，相互协作，对捕获到的猎物按劳分配，弱小的狼自动被淘汰。WPA模型[9]如图2。

图2 狼群捕猎活动

狼群的捕猎空间为N×D，其中,N为狼群的人工狼数量，D为焊点数量，人工狼用Xi表示，Xi=(Xi1，Xi2，…，Xid)，Xi即为焊点序列。目标函数：L=F(X)，L为焊接路径长度。狼群捕猎规则如下：

1)头狼产生：以狼群中目标函数最小的狼为头狼，头狼引领整个狼群，当出现目标函数更小的人工狼时，更新头狼。即：若人工狼目标函数Li小于头狼目标函数Llead，则Llead=Li，Xlead=Xi。头狼不执行3种智能行为。

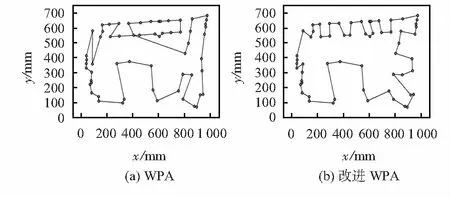
2)游走行为：狼群中探狼负责寻找猎物，游走过程中探狼向t个不同方向游走，计算游走前后的目标函数值，选择目标函数更小的方向前进，前进后更新探狼位置。之后探狼继续游走，直至Li

3)召唤行为：头狼召唤，其余狼向它靠近奔袭，在奔袭过程中，猛狼所在位置目标函数Li小于头狼所在位置目标函数Llead，则更新头狼，新的头狼继续召唤行为，直到与头狼Xlead的距离dis小于或等于所要求的判定距离dnear。猛狼与头狼间的距离采用最长公共子序列[10，11]来计算。判定距离dnear，dnear=1/(D×ω)，ω为距离判定因子。

4)围攻行为：经历过召唤行为的狼，已经距离猎物非常近，而且狼群中人工狼的距离也非常近，在围攻的时候，狼群采用精细化搜索向猎物靠近，围攻前后目标函数值变小，则更新人工狼所在位置，如果没有，则人工狼位置不变。

5)狼群淘汰机制：狼群按强者生存法则，淘汰掉狼群中弱小的狼。即将狼群中目标函数值较差的狼从狼群中淘汰出去，重新产生多条新的狼，以此增加整个种群的多样性。

2.2 WPA改进策略

2.2.1 Logistic混沌初始化

狼群的初始解很大程度影响着狼群最后寻优精度和稳定性，初始解分布不均匀，也将直接影响算法的寻优结果，为使初始种群中的个体更好的遍及整个解空间，减少初始解对算法的影响，本文采用Logistic混沌初始化方法[12]对狼群进行初始化处理，混沌序列产生公式如下

Zi+1=μZi(1-Zi)，i=0，1，2，…，n，μ=4

(2)

其中，0≤Zi≤4，且Zi≠0.25，0.5，0.75。

2.2.2 2-opt算子

狼群围攻过程中，人工狼之间距离已经越来越近，狼群精细化搜索起到的作用越来越少，但狼群精细化搜索所用时间却很长，利用2-opt算子代替狼群围攻行为，可实现细化搜索，提高搜索速度，减少搜索时长。2-opt算子示意如图3所示，选取abcd共4个焊点，若ab的距离加cd的距离大于ac加bd的距离，则反转cb段编码。若没有,则保留。

图3 2-opt算子示意

2.2.3 模拟退火算法

WPA在搜索后期存在着正反馈效应，头狼引领着整个狼群，若头狼没有前进，狼群中所有的狼就会离头狼越来越近，狼群中解的种类就会越来越少，最终就会出现停滞现象。并且WPA中的淘汰机制目的即为增加种群多样性，让算法拥有一定的概率突破局部最优解，但概率实在太小，到算法寻优后期很难找到更好的解。通过引入模拟退火机制，不仅能够有效地增加解的多样性，而且能避免WPA陷入早熟现象。模拟退火算法的引入，就是在所有狼完成一轮搜索后，让头狼作为变换的基础，以一定的概率进行互换、逆转和平移中的一个操作，以产生新的不同解。若新的解总路径更短，则重新计算初始解和新的解偏离度，如果偏离度变小了，则接受新产生的解，如若没有，则以一定的概率接受新的解[13]。接受概率为

(3)

式中p为接受新解的概率，ΔD为新旧解的偏离度差值，T为当前所处的温度，在完成模拟退火操作之后，再进行目标函数更新和降温操作，降温公式为T=T×a，a为降温系数，a∈(0，1)。

3 改进WPA流程

改进WPA步骤如下：1)初始化：初始化狼群规模Nwolf，最大游走次数Smax，退火温度T，冷却因子a，最大迭代次数kmax，距离判定因子ω等参数，logistic混沌初始化每匹人工狼的位置Xi，计算目标函数值Li，选出头狼。执行步骤2。2)探狼游走：当目标函数值Li≤Llead或者达到最大游走步数Smax，转入步骤3，否则，继续游走。3)头狼召唤：若人工狼目标函数Li大于头狼目标函数Llead，则重复召唤行为。若Li≤Llead，则更新头狼，计算人工狼与头狼的距离dis，判断dis与判定距离dnear的大小，若dis≤dnear,则转入步骤4，否则继续召唤行为。4)猛狼围攻：猛狼执行围攻行为，围攻后转入步骤5。5)模拟退火：狼群执行模拟退火操作。6)更新狼群：更新狼群计算目标函数值。7)降温操作：根据式(5)降温操作，若当前温度T小于最小温度Tmin，或者达到循环次数kmax则退出循环，输出最优路径，否则，转步骤2。

4 仿真试验与分析

4.1 TSP仿真分析

机器人焊接路径规划可看作TSP，为验证改进WPA具有一定普遍性，可以适用不同的路径情况，现将基本WPA、改进WPA、蚁群算法和模拟退火算法分别应用于TSP求解，迭代次数为1 000次，重复运行算法30次，做对比分析。验证算法的数据均来自TSPLIB标准数据库。算法的测试环境为个人电脑：Intel®coreTM2.9 GHz，8 GB RAM，在Windows 10系统下的MATLAB R2018a编程测试，算法的各参数由经验和试算得到。由表1可以看出，在算例Burma14,Oliver30,Eil51和Pr76中，改进WPA具有较好的寻优能力，相比其他3种算法，改进WPA在4个案例中均寻找到了已知最优解，偏差为0，收敛率为100 %，具有明显优越性。

表1 4种算法的寻优结果对比

仿真试验证明，改进WPA具有良好的收敛性能和寻优能力，可以适用不同的路径情况。图4为改进WPA在以上算例上的最优解路径。

图4 改进WPA路径寻优

4.2 车门焊点路径规划仿真分析

将改进WPA运用到车门焊接路径规划任务中，以上汽荣威某车型车门焊接模型为例，分别利用基本WPA和改进WPA对焊接任务进行路径规划，算法迭代次数250次，重复运行30次，取单次和多次算法寻优结果进行对比分析。图1(b)为某种车门实物，均匀的取车门上的60个焊点做仿真。图5(a)为基本WPA规划的结果，最终得到的焊接路径最短长度为5 457.130 9 mm，路径规划所用时间为268 s。图5(b)为改进WPA的机器人焊接路径规划的结果，最终得到的最短焊接路径长度为4 592.384 5 mm，路径规划所用时间为28 s。改进WPA在MATLAB仿真中，最短焊接路径为：1—2—3—4—5—6—7—8—9—10—11—12—13—52—53—14—15—51—50—16—17—49—46—47—45—20—21—22—44—43—23—24—25—26—27—28—29—42—41—59—30—31—40—58—33—32—34—35—39—57—36—56—60—55—54—37—38—1。

图5 2种算法寻优路径

图6为基本WPA和改进WPA在焊接路径中的单次和多次寻优路径对比，可以看出，改进WPA的收敛速度明显高于基本WPA，改进WPA在迭代50次左右就开始收敛，而基本WPA在迭代70次左右才开始收敛。在搜索过程中，改进WPA在迭代60～80次时能很好地跳出局部最优解，在迭代100～130次时就能寻找到最优解，而基本WPA并不能有效地跳出局部最优，且会发生停滞现象。从算法单次寻优结果上看，改进WPA最短路径比基本WPA减少了864.74 mm，总路径缩短了15.8 %，且在路径规划时间上减少了4 min，所用时间缩短了89.5 %。

图6 单次、平均寻优路径对比

5 结 论

本文改进的WPA具有很好的普适性，能够适用于不同的路径，寻优偏差小且收敛率高；从焊点路径规划试验结果分析，改进WPA在路径规划任务中取得了明显的效果，解决了基本WPA寻优过程中的不足；通过引入Logistic混沌初始化、2-opt算子和模拟退火算法对WPA进行的改进是有效的，改进WPA能够很好的适用于焊接路径规划任务中，提出的改进策略缩短了算法运行时间，增加了算法精度，成功帮助算法在路径规划中跳出了局部最优解，大大提高了算法性能和焊接效率。