适应航天力学环境的质量检测器设计与仿真

2022-12-10周文兴蔡红华杨云凯刘俊杰杨清宇

传感器与微系统 2022年12期

周文兴，蔡红华，杨云凯，黄刚，刘俊杰，杨清宇

(1.航天员科研训练中心,北京 100094; 2.西安交通大学电子与信息工程学院,陕西西安 710049)

0 引言

四极质谱仪因为其优异的性能在航天领域被广泛应用。所有的设备产品在应用于航天领域时都要进行复杂苛刻的力学环境适应性分析和设计[1～8]，质量检测器作为四极质谱仪的核心部件，是用于化学分析的精密仪器，内部组件精密且抗复杂力学性能较差，需要优化内部组件结构设计，保证整机在经历复杂力学环境的优良性能。

通过仿真分析和试验验证进行产品设计是目前常使用的有效手段，本文采用有限元分析(FEA)法对质量检测器在复杂力学环境下的适应性进行计算分析，并开展力学试验对结构设计进行有效验证。

1 质量检测器结构设计

1.1 质量检测器结构形式

质量检测器分为离子源端和四极分析器端，两部分分别装配在质谱腔上，均通过法兰进行硬连接，保证其良好力学环境适应性。离子源端装配进质谱腔长度为63.5 mm，重量为120 g；四极分析器端装配进质谱腔长度为202.1 mm，重量为385 g。

1.2 质量检测器的结构特性

离子源端全部使用金属材料硬连接，并且通过法兰进行固定，不存在结构设计风险。四极分析器段全部使用金属材料硬连接，通过法兰进行固定，但由于长度较长，且固定连接使用螺钉连接，螺钉固定连接图和螺钉承力部分截面如图1。因此，重点对四极分析器端进行结构分析，并进行环境适应性设计优化和分析验证。

图1 螺钉固定示意与承力部分截面

2 三维仿真分析

2.1 有限元分析方法[9，10]

1)结构离散化

在结构理想化的基础上，将结构划分成有限个单元，并在指定的各个单元设置节点，把各个单元节点连接起来作为一个整体等效原结构。

2)选择位移函数

对单元的位移分布做出假定来定义单元的形状和节点。其中位移分布与形状函数NN有关。则单元体内任意一点的广义位移U定义为单元节点变量uN,e的表达式为

Ue=NNuN,e

(1)

3)单元的力学特性分析

通过几何方程推导出单元应变关系的表达式为

εe=BNuN,e

(2)

通过材料本构关系推导出单元应力的表达式为

σe=DBNuN,e

(3)

令初应力、初应变分别为σ0、ε0，则应力表达式为

σe=DBNuN,e-Dε0+σ0

(4)

4)等效节点的计算

单元上的体力、集中力和单元边界上的力必须作用在节点上，用节点上的力等效单元上的力。则单元节点力的表达式为

(5)

当有初应力σ0和初应变ε0时，则单元节点力的表达式为

(6)

5)整体结构平衡方程的建立

将单元的整体刚度矩阵等效结构总体的刚度矩阵，将单元节点上的力等效结构总体上的各个载荷，建立整个结构的平衡方程

∑Keü=F

(7)

单元的刚度矩阵为

(8)

将单元坐标系到整体坐标系的变化代入单元等效节点力和单元刚度矩阵进行求解。

6)结构平衡方程的求解

应用位移边界条件，化解总体刚度矩阵的奇异性，进而得到线性方程组，求解方程组得到各个节点的位移。

7)单元应力和单元应变的计算

结构静力学和动力学的分析过程类似，只是结构动力学在计算等效节点力时不包含体力项，而被单元质量矩阵和广义加速度矢量的积替代，则整体结构的平衡方程的表达式为

∑Meü+Ku=FS

(9)

其中单元质量矩阵为

(10)

求解整体结构的平衡方程可以得到所需要的节点位移和加速度。

2.2 计算网格与边界条件

质量检测器整体计算网格如图2所示，有限元计算网格共有节点449 096个，单元240 624个；重点关注螺钉和锁紧螺母部位局部网格分别如图 3(a)和(b)所示。

图2 质量检测器有限元计算网格

图3 零部件螺钉部位局部网格

2.3 仿真结果分析

对产品进行正弦振动试验和随机振动试验[11，12]，质量检测器被系统给定响应条件表明，同一外界条件下，其正弦响应的应力值比随机响应小，这里主要分析随机振动下的应力响应见表 1，响应输入点位于法兰表面，静载荷等效计算时按照3σ准则进行。

表1 随机振动试验条件

2.3.1 原设计方案仿真结果分析

质量检测器结构设计方案中倍增器屏蔽桶底部与法兰连接使用M2×6不锈钢螺钉，锁紧螺母端未使用固定辅助手段，分别对X,Y,Z共3个振动方向力学环境试验条件进行响应分析，重点分析连接处M2×6螺钉的适用性，不锈钢螺钉的材料参数见表 2。不同规格螺钉尺寸为：1)M2×6螺钉小径直径1.567 mm，截面面积1.93 mm2；2)：M3×6螺钉小径直径2.5 mm，截面面积4.9 mm2。

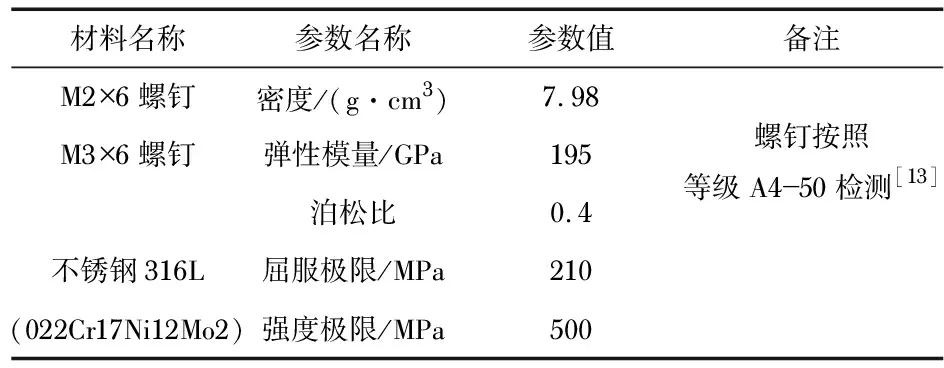
表2 关注点螺钉材料参数

本文分析质量检测器的高频随机振动力学环境适应性主要针对5～2 000 Hz能量范围[14]。针对3个不同轴向方向的随机振动激励条件进行仿真分析，得到锁紧螺母上测点响应均方根加速度值和螺钉截面的平均等效应力如表 3所示，每个轴向应力最大螺钉的截面平均等效应力分布云图如图4所示，与表 2中螺钉的屈服极限和强度极限对比可知，原设计方案下螺钉无法满足给定的随机振动条件下的使用需求。

图4 仿真得到M2×6螺钉截面上等效应力分布

表3 随机振动条件下M2×6螺钉截面的平均等效应力

2.3.2 优化设计与仿真结果分析

由原设计方案的仿真分析结果可知，原设计方案中M2规格螺钉不满足力学环境试验条件使用要求，锁紧螺母端未进行辅助固定形成“悬臂梁”结构的力学环境适应性较差。针对上述分析结论对质量检测器结构设计进行优化：1)将M2螺钉更改为M3螺钉；2)在锁紧螺母端使用定位环进行径向(X向和Z向)固定。

针对优化设计方案进行3个不同轴向方向的随机振动仿真分析，得到锁紧螺母上测点响应均方根加速度值和螺钉截面的平均等效应力如表 4所示，与原设计方案仿真结果表 3对比发现，在锁紧螺母端增加定位环消除了“悬臂梁”效应，大幅降低了锁紧螺母的振动响应，明显提升了对随机振动的力学适应性。

表4 随机振动条件下M3×6螺钉截面的平均等效应力

结合优化设计方案的每个轴向应力最大螺钉的截面平均等效应力分布云图如图5所示，与表 2中螺钉的屈服极限和强度极限对比可知，优化后设计方案下螺钉能够充分满足给定随机振动条件下的使用需求，并且有充足的设计冗余。

图5 仿真得到M3×6螺钉截面上等效应力分布

3 试验验证

3.1 试验条件

装配质量检测器试验件进行结构设计的力学试验验证，随机振动试验条件由其所经历的真实力学环境制定，总均方根加速度值为10.58grms(加载方向包括X/Y/Z3个轴向)，试验过程中质量检测器安装工况图 6所示。试验条件控制点设置在试验平台上，试验过程中质量检测器安装在质谱腔内，安装边界条件保持与工作状态一致。