网络谣言传播的动力学建模及其平衡点稳定性分析

2022-12-08高卫国蔡永丽

扬州大学学报（自然科学版） 2022年5期

高卫国, 蔡永丽

(淮阴师范学院 a. 计算机科学与技术学院; b. 数学与统计学院, 江苏淮安 223300)

随着互联网技术的飞速发展,谣言传播方式逐渐从人与人之间的口口相传演变为通过微博、微信和抖音等新媒体社交平台传播, 且具有传播速度快、影响范围广和危害程度高等特点, 故突发事件中网络谣言传播规律的研究尤为重要. 1964年, Daley等[1]率先利用传染病动力学方法将人群分为无知者、传谣者以及听说过谣言但不传谣者三类,研究了谣言传播规律.此后, 大批学者应用动力学模型探讨谣言传播机理,并为制定抑制网络谣言扩散的相关策略提供了科学依据. Zhao等[2]考虑不同传谣者之间的通信对谣言传播的影响 ,建立新的易感者-感染者-易感者(susceptible-infectious-susceptible, SIS)谣言传播模型, 验证行波解的存在性, 并分析了不同扩散形式对谣言传播的影响; Zhang等[3]认为真实信息传播者的初始值越大谣言传播者的峰值越小, 谣言传播终止时间则越短; Huo等[4-6]考虑异质网络中的社会强化和遗忘因素, 证实谣言的最终大小与社会强化程度相关, 还探讨了考虑心理因素和时滞的谣言传播模型的最优控制问题, 通过建立具有脉冲效应的官方信息与谣言传播之间的相互作用模型,得到谣言消除和系统持久性的阈值; Yin等[7]探讨了谣言和反谣言对信息传播动力学的影响机制; Sun等[8]考虑心理因素对谣言传播的影响建立了谣言传播模型, 结果表明信任和关联机制会扩大谣言规模和缩短终止时间; Cheng等[9]通过删除谣言帖子或实施科普教育等策略控制谣言传播规模并优化成本; 赵敏等[10]建立了一类具有政府控制效应的社交网络谣言传播模型, 结果表明政府等相关部门采取积极的应对策略有利于谣言传播的有效控制. 谣言传播的影响机制颇多,如监管机构对谣言的监管效应[11]、空间因素[12-13]及随机因素[14-15]等．本文拟考虑政府干预效应和智者影响力等因素对网络谣言传播的影响, 运用传染病仓室动力学建模方法建立新的网络谣言传播动力学模型,并通过平衡点的稳定性分析和数值模拟研究网络谣言的传播规律及其相应的控制措施.

1 模型建立

借鉴传染病动力学建模方法将总人群N分为3个“仓室”, 记为u,v,w,分别代表无知者(对谣言一无所知且不具备辨识能力者)、传谣者(肆意传播谣言者)和智者(听说过谣言但不传播谣言且能够进行真相剖析并传递正确信息者)的密度．建立谣言传播的微分方程模型:

(1)

其中输入率常数Λ=μN, 移出率μ表示个体由于对事件本身失去兴趣而退出系统的概率,N=u+v+w;α为传播率;β为无知者与智者的接触率;δ为传播者与智者的接触率;r为传播者进入智者仓室的速率;av/(1+bv) 表示政府部门干预对谣言传播的影响,a为政府干预效应参数,b为饱和系数.参数Λ,α,β,μ,δ,r,a,b均为非负常数．

由于u+v+w=N, 所以仅须通过简化的平面系统

(2)

研究模型(1)的动力学行为．

2 平衡点的存在性及稳定性

1) 模型(2)始终存在灭绝平衡点E0=(0, 0),传谣者v和智者w都被移出系统,即谣言系统消失;

2) 当β>μ/N时, 模型(2)存在边界平衡点E1=(0, (Nβ-μ)/β), 传谣者v消失而智者w持续存在, 即谣言不攻自破;

3) 当满足条件(H)

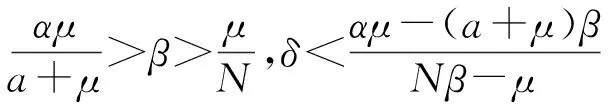
定理1模型(2)的平衡点局部稳定性结果如下:

1) 当β≤μ/N且α<(a+μ)/N时,E0是局部渐近稳定的;

2) 当β>μ/N且α<β(a+μ)/μ时,E1是局部渐近稳定的;

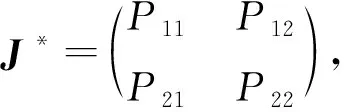
定理2对于模型(2), 当条件(H)成立且α>ab-r时,E*是全局渐近稳定的.

3 数值模拟与结果分析

下面根据定理1～2进行数值模拟研究3类平衡点的稳定性,以期进一步研究网络谣言传播规律以及最终扩散状态,从而为控制网络谣言传播措施的制定提供科学依据.

3.1 灭绝平衡点E0的稳定性

由定理1可知, 当β<μ/N且α<(a+μ)/N时, 模型(2)的解最终收敛到灭绝平衡点E0=(0,0), 即传谣者和智者都被移出系统, 谣言系统消失.选取参数α=0.2,N=2,δ=0.01,a=0.01,b=0.3,μ=0.5,β=0.2,r=0.5, 模型(2)的解趋于E0=(0,0)时的动力学行为如图1所示.由图1可知, 谣言自身没有吸引力, 随着时间的推移, 谣言消失.

图1 灭绝平衡点E0的稳定性Fig.1 The stability of the extinction equilibrium E0

3.2 边界平衡点E1的稳定性

由定理1可知, 当β>μ/N且α<β(a+μ)/μ时, 边界平衡点E1局部渐近稳定, 即最终谣言传播者移出系统.选择参数α=0.2,N=2,δ=0.01,a=0.01,b=0.3,μ=0.5,β=0.3,r=0.5, 模型(2)的解趋于平衡点E1=(0,0.33)时的动力学行为如图2所示.由图2可知, 该情形下谣言传播者v趋于0,而智者w持久存在,智者的公信力较高,网民在其正确引导下对谣言具有一定的辨识能力,并且不信谣、不传谣,最终传播者被移出系统,谣言销声匿迹.

图2 边界平衡点E1的稳定性Fig.2 The stability of the boundary equilibrium E1

3.3 共存平衡点E*的稳定性

图3 共存平衡点E*的全局稳定性Fig.3 The stability of the coexistence equilibrium E*

3.4 谣言传播控制

为了进一步研究谣言传播规律, 现通过数值模拟分别探讨传谣者与传播率α、接触率β、移出率μ以及政府干预效应a之间的关系, 结果如图4所示.由图4可见: 1) 随传播率α的增大,v(t) 逐渐增加.表明降低传播率α在很大程度上可以减少传谣者的数量; 2) 随接触率β或移出率μ的增大,v(t)均呈现逐渐下降的趋势.表明加强智者与无知者接触,或网民对谣言兴趣的衰减都可有效控制谣言传播; 3) 随政府干预效应a的增大,v(t) 逐渐降低.表明政府部门的干预能够有效控制谣言的传播.