基于组合式信号的Hammerstein系统两阶段辨识

2022-12-08张明光王正群

扬州大学学报（自然科学版） 2022年5期

俞洋, 张明光, 李峰, 王正群

(1. 江苏理工学院电气信息工程学院, 江苏常州 213001; 2. 扬州大学信息工程学院, 江苏扬州 225127)

Hammerstein系统是一类由静态非线性模块和动态线性模块串联组成的非线性动态系统, 具有易辨识、计算量少和非线性逼近能力强等特点, 被广泛用于描述非线性过程[1]．目前, 对于Hammerstein系统的辨识主要分为同步辨识和分步辨识两大类[2-4]．实际工况下, 系统易受测量噪声和时滞的干扰, 故噪声和时滞干扰下的Hammerstein系统辨识研究具有重要意义．Ma等[5]针对Hammerstein时滞系统探讨了基于卡尔曼滤波的最小二乘迭代算法和递推最小二乘算法; Wang等[6]针对Hammerstein状态空间系统,提出基于数据滤波技术的多新息随机梯度辨识方法; Dong等[7]考虑一类具有动态扰动和测量噪声的Hammerstein系统,提出一种扩展递推最小二乘辨识算法; Prasad等[8]针对具有输入延迟和死区的Hammerstein系统, 提出了一种新的基于分离死区参数和分数阶参数的辨识策略; Wang等[9]将具有子空间状态空间线性元素的Hammerstein输入非线性系统转化为双线性辨识模型, 并提出一种递归和迭代最小二乘辨识算法．上述方法尽管能够辨识Hammerstein系统,但仍存在下述问题: 1) 辨识方法中包含的静态非线性模块和线性模块参数的乘积项增加了辨识复杂度, 须通过参数分解技术分离混合参数以提升辨识精度; 2) 对于强非线性或不连续的非线性系统,采用多项式或分段函数建模时的精度较低．本课题组在前期工作[10]中发现当输入为可分离信号且存在常数的情况下, 可用静态非线性系统的自相关函数替代其互相关函数解决中间变量信息不可测问题, 从而实现静态非线性模块和动态线性模块的分离辨识．本文拟针对含测量噪声和时滞的神经模糊Hammerstein非线性系统,设计一种由可分离信号和随机信号相结合的组合式信号, 利用相关性分析方法和辅助模型递推最小二乘法分别辨识Hammerstein系统线性模块和静态非线性模块的参数,以期实现静态非线性模块和动态线性模块的分离辨识．

1 问题描述

考虑如图1所示的含测量噪声和时滞的神经模糊Hammerstein非线性系统, 利用神经模糊模型[11-12]逼近静态非线性模块f(·), 利用时滞状态空间模型逼近动态线性模块L(·)．

图1 神经模糊Hammerstein系统结构示意图Fig.1 Structure diagram of neuro-fuzzy Hammerstein system

Hammerstein系统的输入/输出数学表达式为:

v(k)=f(u(k));
x(k+1)=Ax(k)+Bx(k-1)+hv(k);
ω(k)=cx(k);
y(k)=ω(k)+e(k),

(1)

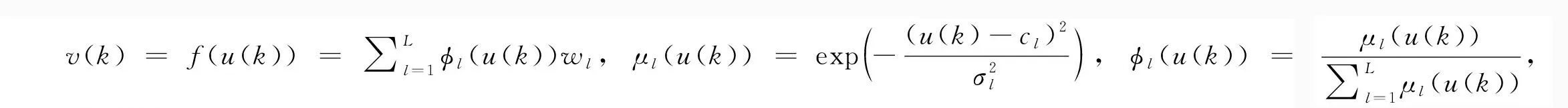
定义adj[X]为方阵X的伴随矩阵, det[X]为方阵X的行列式,z-1为单位后移算子, 则x(k-1)=z-1x(k),x(k+1)=zx(k)．根据单位后移算子的特性, 将Hammerstein系统(1)转化为输入/输出形式:

(2)

式中b(z)=z-2n+1cadj[z2I-Az-B]h=b1z-1+…+a2n-1z-(2n-1),I为合适维数的单位矩阵,a(z)=z-2ndet[z2I-Az-B]=1+a1z-1+…+a2nz-2n．

对给定的阈值ε, 建立神经模糊Hammerstein系统, 计算满足下述条件的参数:

(3)

2 神经模糊Hammerstein系统辨识

为了实现Hammerstein系统的静态非线性模块和动态线性模块的分离辨识, 现设计一种由高斯信号u1(k)及其输出y1(k)和随机信号u2(k)及其输出y2(k)相结合的组合信号．

2.1 动态线性模块

根据式(2)可得Hammerstein系统高斯输入信号u1(k)的输出

(4)

式中ai,bj为线性模块的参数;na,nb为阶次,na=2n,nb=2n-1．在式(4)两边同时乘以u1(k-τ)并计算其数学期望, 可得

(5)

式中Ry1u1(τ)=E(y1(k)u1(k-τ))为u1(k)和y1(k)的互相关函数,Rv1u1(τ)=E(v1(k)u1(k-τ))为v1(k)和u1(k)的互相关函数,Reu1(τ)=E(e(k)u1(k-τ))为e(k)和u1(k)的互相关函数,E(·)表示数学期望,τ为时间常数．

由白噪声序列e(k)的均值为零可得E(e(k))=0, 由于白噪声序列e(k)和输入u1(k)是相互独立的, 则E(e(k)u1(k))=E(e(k))E(u1(k))=0, 故Reu1(τ)=0．于是, 有

(6)

利用相关性分析法辨识动态线性模块的参数．假设τ=1,2,…,P(P≥na+nb), 则动态线性模块的参数

(7)

2.2 静态非线性模块

利用神经模糊模型逼近静态非线性模块．神经模糊模型中须辨识的参数包含中心cl、宽度σl及权重wl, 其中中心cl和宽度σl采用聚类算法[12]辨识．下面讨论权重wl的辨识．

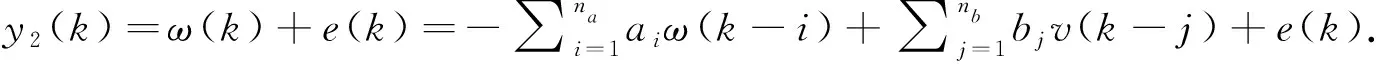
y2(k)=ξT(k)γ+e(k),

(8)

式中参数向量γ=[a1,…,ana,b1w1,…,b1wL,…,bnbwL]T, 信息向量ξ(k)=[-ω(k-1),…,-ω(k-na),φ1(u2(k-1)),…,φL(u2(k-1)),…,φL(u2(k-nb))]T．由式(8)可见信息向量ξ(k)中存在不可测变量ω(k), 故Hammerstein系统的参数辨识无法通过计算获取．现运用辅助模型技术[13]解决该问题, 即利用辅助模型的输出ωa(k)代替辨识系统中的不可测变量ω(k)．定义ξa(k)和γa分别为k时刻辅助模型的信息向量和参数向量, 则辅助模型的输出

(9)

定义准则函数

(10)

(11)

(12)

(13)

(14)

3 数值仿真

应用2016a MATLAB软件进行数值仿真, CPU为Intel Core i7-6700HQ, 主频2.60 GHz, GPU为NVIDIA GeForce GTX950M, Windows 10 64位操作系统．为了验证本文两阶段辨识方法的有效性, 考虑含测量噪声和时滞的Hammerstein系统:

(15)

y(k)=[1,0]x(k)+e(k),

其中系统的静态非线性模块v(k)是不连续函数．

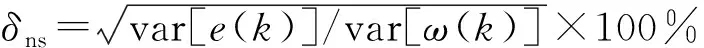
图2 不同噪信比下线性模块参数a1,a2,a3,a4的估计Fig.2 Estimation of linear module parameters a1, a2, a3, a4 at different noise-to-signal ratios

图3 不同噪信比下线性模块参数b1,b2,b3的估计Fig.3 Estimation of linear module parameters b1, b2, b3 at different noise-to-signal ratios

由图2～3可见: Hammerstein系统训练样本总数为5 000, 当噪信比为10.94%, 训练样本数为1 000～1 500时, 动态线性模块参数a1,a2,a3,a4,b1,b2,b3的估计值接近真实值, 且随数据长度的增加, 参数估计精度逐渐提高, 估计曲线趋于稳定; 当噪信比增加至20.51%, 训练样本数达1 500～2 000时, 动态线性模块参数a1,a2,a3,a4,b1,b2,b3的估计值接近真实值, 且随训练样本数的增加,参数估计精度逐渐提高并趋于稳定．故本文提出的相关性分析法可有效辨识动态线性模块的参数．