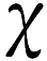有限元Crank-Nicolson格式高阶求解非稳态扩散方程
2022-12-08王晓莹
王晓莹, 刘 雪, 江 山
(南通大学理学院, 江苏 南通 226019)
非稳态扩散问题广泛存在于流体力学、化工制造、环境科学和能源开发等领域.在实际应用中, 主要采用有限差分法[1-2]、有限体积法[3-4]、谱方法[5-6]或有限元法[7-10]等数值方法进行求解.上述方法大多需要一定的限制条件, 如Gowrisankar等[1]在解决非稳态抛物型初边值问题时, 须运用迎风有限差分格式在时间层的等分布原理; Quenjel[3]提出的全隐格式有限体积法, 需要在多边形网格上才能更好地保证数值解的非负性.然而, 有限元法的优势在于可以针对不同的微分方程建立对应的变分形式以适应不同的问题, 在有限单元离散剖分背景下参考单元与实际单元之间形成必要的仿射变换, 并通过独立构造的多项式基函数有效耦合局部与全局间的空间尺度信息, 得到精度更好、收敛更快的模拟结果.如Cheng等[7]利用局部间断有限元法处理奇异摄动非稳态问题, 给出全离散时间在三阶龙格-库塔法的误差分析; Lin等[8]提出一种对流扩散反应方程的流线迎风Petrov-Galerkin(streamline-upwind Petrov-Galerkin, SUPG)稳定化时空有限元法, 得到了时空数值格式的误差估计; Varma等[10]针对非稳态对流扩散反应方程, 分析了自适应有限元法的后验误差.近年来, 利用多种数值方法相结合进行优势互补的措施备受关注.如Das等[11]针对奇异摄动延迟抛物方程, 在Shishkin网格应用有限元与有限差分的混合计算格式得到一致收敛; Li[12], Mekonnen[13]等分别利用迎风格式的本征正交分解与混合有限差分格式有效模拟了双参数非稳态模型.此外, 通过构造特殊函数与边界元技术, 在二维情形紧凑型的高阶计算格式也取得相关进展[14-15].截至目前, 尚未出现文献报道在空间上应用高次有限元法与时间上应用θ=0.5的Crank-Nicolson有限差分隐格式相结合求解时空间非稳态的对流扩散反应方程.本文拟基于高次有限元法结合Crank-Nicolson有限差分格式求解非稳态对流扩散反应方程,以期获得精确化的高阶一致收敛模拟结果.
1 问题提出
考虑非稳态对流扩散反应方程
(1)
其中u为原时空问题的真解,x为空间变量,t为时间变量,α,β,χ为方程系数,f为方程右端项.设定初边值条件:
u(x,0)=u0,x∈[a,b];
(2)
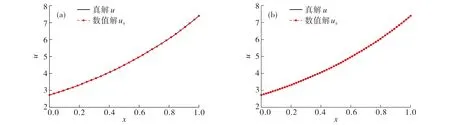
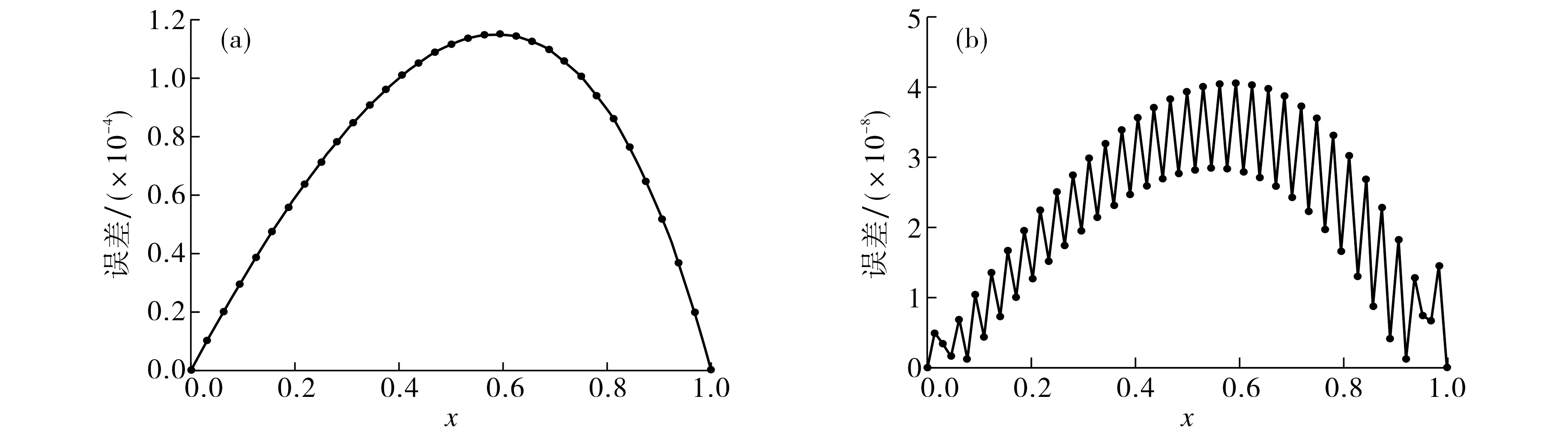
u(a,t)=ua,u(b,t)=ub, 0 (3) 本文研究目的是得到真解u的精确化高阶数值逼近结果uh. 根据虚功原理, 在问题(1)左右两边同时乘以检验函数v, 在区间I=[a,b]进行积分,得 (4) 限定检验函数满足v(a)=v(b)=0, 在此基础上利用分部积分化简式(4)得 (5) (6) Galerkin方法通过有限维空间近似无限维空间.记有限元空间Uh为无限维空间H1(I)的子空间, 即Uh⊂H1(I), 再记uh为空间的有限元解函数, 其中h为空间步长, 则问题(1)的半离散Galerkin格式为: 寻找uh∈H1(0,t;Uh), 满足 (7) 在半离散Galerkin格式(7)中, 有限维空间Uh是在有限元格式下由分片多项式构造的基函数张成.本文中, 有限单元上的基函数通过“参考元→局部元→全局元”的模式构造, 现以二次基函数为例描述其构造过程. (8) (9) (10) (11) (12) 由此可得局部有限元空间Sh(Ihn)=span{ψn1,ψn2,ψn3}. 4) 在剖分形成的每一个全局节点xj(j=1,2,…,Nb)处定义全局基函数, 使得φj|Ihn∈Sh(Ihn)且满足条件 (13) 其中φj(j=1,2,…,Nb)为所张成有限维空间的基函数数目.类似地, 可构造线性有限元基函数及其张成的有限维空间,且线性有限元基函数张成有限维空间时, 多项式次数和节点数据对应关系较二次有限元更简单. (14) 其待定系数为u1(t),u2(t),…,uNb(t). 将方程组(14)进一步以向量和矩阵形式表示, 则可得到对应的代数系统为 MX′(t)+A(t)X(t)=b(t), (15) 采用有限差分法对系统(15)的时间尺度进行全离散.将问题(1)中时间(0,T]一致剖分成Nm个步长为ht的时间层单元, 时间节点为tm=mht,m=0,1,…,Nm.于是, 经过时间尺度离散, 可得系统(15)的全离散格式 (16) 其中θ为具体格式的参数, 其取值决定着时间层的差分格式.当θ=0时为向前差分格式, 这种显格式虽可直接迭代且无须解方程组, 但其稳定性差,会导致误差传播不可控; 而当θ=1、θ=0.5时分别为向后差分格式和Crank-Nicolson六点对称格式, 均为隐格式,虽然都需要求解方程组,但是稳定性和数值精度更佳.故本文分别选择向后差分格式和Crank-Nicolson对称格式进行时间离散. 令θ≠0, 定义Xm+θ=θXm+1+(1-θ)Xm, 则有 (17) 将式(17)代入全离散Galerkin格式(16), 化简得 (18) (19) 求解系统(19), 可得未知向量组Xm+θ. (20) 为了清晰有效地对比验证数值解的真实效果,在空间处理的有限元格式分别采用线性有限元法和二次有限元法, 由此形成从局部单元到全局单元的构造与组装.在时间处理的有限差分格式分别取θ=1及θ=0.5的2种隐格式差分, 由此对全离散系统(19)进行求解, 最终得到数值解uh.为了度量uh对方程(20)的真解u的逼近效果, 在t时刻分别计算二者误差的L∞范数、L2范数及H1半范数: ‖u-uh‖∞=supx∈I|u-uh|, (21) (22) (23) 再利用上下层空间剖分形成的粗网格和细网格对应的误差范数值EN,E2N, 计算3种范数各自的收敛阶数 (24) 进而根据收敛阶数验证数值方法的稳定性和收敛速度. 将空间步长h与时间步长ht的关系固定为ht=h2, 采用线性有限元法分别结合θ=1、θ=0.5两种时间全离散隐格式, 计算问题(20)在空间剖分数N不断偶数倍增大时的数值解uh,并根据式(21)~(24)分别计算两种差分格式下数值解与真解之间的3种误差范数及相应收敛阶, 结果如表1~2所示.由表1~2可见:两种差分格式下, 3种误差范数值随空间剖分数N偶数倍增大而不断递减,表明数值解与真解的逼近越来越好;L∞范数和L2范数均有清晰的二阶收敛,H1半范数有清晰的一阶收敛,保证了线性有限元法结合时间层计算的可靠性和稳定性;θ=0.5的Crank-Nicolson差分格式下数值解的逼近效果稍优于θ=1的向后差分格式. 表1 θ=1时线性有限元的误差范数和收敛阶Tab.1 Error norm and convergence order of linear finite elements, θ=1 表2 θ=0.5时线性有限元的误差范数和收敛阶Tab.2 Error norm and convergence order of linear finite elements, θ=0.5 类似地, 取空间步长h与时间步长ht的关系为ht=h2, 当空间剖分数N偶数倍增大时, 采用二次有限元法分别结合θ=1、θ=0.5两种时间全离散隐格式求解问题(20), 并计算相应的误差范数和收敛阶, 结果如表3~4所示.由表3~4可见:θ=1的向后差分格式下,L∞范数、L2范数及H1半范数均有二阶收敛;θ=0.5的Crank-Nicolson对称差分格式下,L∞范数、L2范数达到三阶收敛, 而H1半范数也能达二阶收敛; 应用二次有限元法结合两种不同的时间全离散隐格式求解时,θ=0.5的收敛性结果明显优于θ=1时的, 二次有限元法在θ=0.5的Crank-Nicolson隐格式下精度更高,收敛更快. 表3 θ=1时二次有限元的误差范数和收敛阶Tab.3 Error norm and convergence order of quadratic finite elements, θ=1 表4 θ=0.5时二次有限元的误差范数和收敛阶Tab.4 Error norm and convergence order of quadratic finite elements, θ=0.5 分别选定ht=h2,θ=1和ht=h2,θ=0.5, 对比分析线性有限元法和二次有限元法在空间尺度求解问题(20)时的误差精度及收敛阶.由表1和表3可知, 二次有限元法的误差范数值明显优于线性有限元法的, 其结果更为精确, 误差精度更高.由表2和表4可知, 二次有限元法的数值精度较线性有限元法高103倍或以上, 且3种范数的收敛阶全部提升了一阶,L∞范数、L2范数达三阶,H1半范数达二阶. 图1给出了t=1 s时分别采用线性有限法和二次有限元法结合Crank-Nicolson对称差分格式求解问题(20)得到的数值解uh与真解u.由图1可见,无论是采用线性有限元法还是二次有限元法,在最简便且较稀疏的一致网格剖分数N=32上计算皆可实现数值解uh对真解u的完美逼近.其中,由于二次有限元法在对空间尺度进行剖分时自由度加入了单元中点, 所以使得数值解uh在图1(b)显示更密集, 这表明本文方法求解一维非稳态对流扩散反应问题的有效性与稳定性较高. 图1 当θ=0.5、t=1 s时,线性有限元(a)与二次有限元(b)在N=32下的真解和数值解Fig.1 When θ=0.5, t=1 s, the exact solution and the numerical solution of linear finite element (a) and quadratic finite element (b) on N=32 图2给出了真解u与数值解uh之间的绝对误差|u-uh|.由图2可见, 在t=1 s时采用线性有限元法和二次有限元法模拟结果的精确度均较高.由于二次有限元法是基于线性有限元法, 在空间尺度进行单元剖分时再取同一单元步长的中点作为单元新节点,所以依次连接所有离散节点的误差值时会出现图2(b)所示的上下振荡情况,且二次有限元法的误差在较粗剖分数N=32上更是达到了10-8数量级, 再次验证二次有限元求解非稳态问题的优越性. 图2 当θ=0.5、t=1 s时, 线性有限元(a)与二次有限元(b)在N=32下的绝对误差Fig.2 When θ=0.5, t=1 s, the absolute error of linear finite element (a) and quadratic finite element (b) on N=32 综上分析,本文利用空间上的二次有限元法,结合时间上的Crank-Nicolson有限差分隐格式, 精确有效地模拟了一维非稳态对流扩散反应问题.数值算例表明,在一致网格进行等距的时空间步长离散后可以获得理想结果,二次有限元结合Crank-Nicolson有限差分隐格式求解时的计算精度和收敛阶数更高,应用优势更明显.2 空间尺度的有限元法
2.1 有限元变分形式
2.2 半离散Galerkin格式


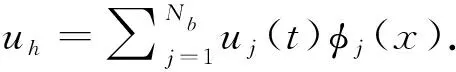
3 时间尺度的全离散格式

4 数值实验