基于动态时间规整的纱线毛羽H值周期模式识别方法
2022-12-08王波波朱闯闯郑小虎汪俊亮鲍劲松
王波波, 朱闯闯, 郑小虎, 汪俊亮, 鲍劲松
(东华大学 a.机械工程学院,b.人工智能研究院,c.上海工业大数据与智能系统工程技术研究中心, 上海 201620)
毛羽是衡量纱线质量的重要性能指标之一[1]。纱线毛羽对纱线的性能、品质和后序加工过程影响显著[2-4]。毛羽产生于细纱,增加于络筒工艺。在粗纱经细纱机拉伸、加捻变为细纱的过程中,细纱机上与纱线直接接触的各个部件都对毛羽生成有一定程度的影响[5-6]。这些部件或周期性地作用在纱线上,或带动纱线和其他部件周期性地接触,导致毛羽的生成在短期和长期上也呈现周期性。
目前,文献研究多针对与纱线直接接触的某单个细纱机部件对纱线毛羽生成的周期性影响。如:余豪等[7]通过理论推导证实导纱钩周期性上下往复运动会引起纺纱三角区几何面积发生规律性变化,并通过试验证实纱线毛羽指数的周期性。兰小鹏[8]在研究钢丝圈的整个生命周期对毛羽指标的影响时发现,钢丝圈的生命周期符合磨合期、稳定期和衰退期的规律,该规律也是毛羽在稳定状态下的长期周期模式,其中周期模式是指周期时间或周期数据长度上毛羽数据的变化。
毛羽H值是纱线毛羽评估指标之一,是无量纲值,其值等于1 cm测试长度内纱线毛羽的累计长度之和。研究毛羽H值的周期模式对提高纱线质量有着重要意义。实际中,毛羽H值不仅反映多个直接与纱线接触的细纱机部件对毛羽生成周期性影响的叠加效果,还受到部件的运行参数、环境温湿度和原材料等的影响。但从这些方面考虑诸如钢丝圈的型号、罗拉的转速、温湿度和长绒棉等特征参数与毛羽H值的建模和映射关系是非常复杂的,相反从具有周期性的毛羽H值数据中提取周期模式更为简单直接。
理想状态下,毛羽H值在周期时间下的周期数据长度是一个固定值。但实际上纱线在生产或检测时受力不均匀,导致毛羽H值的周期数据长度和毛羽在纱线上的特征分布发生变化。本文旨在从周期数据长度不断变化的毛羽H值数据中提取具有代表性的周期模式。距离函数是衡量模式与样本、样本与样本之间相似度的一类方法[9],如余弦相似度[10]、欧几里得距离和动态时间规整(dynamic time warping,DTW)[11]等。由于欧几里得方法只能计算两个长度相同的序列,因此无法通过欧几里得距离确定周期模式[12]。而DTW算法能够计算两个不同长度的序列,并可得到最优的规整路径,但DTW算法的复杂度较高。本文研究了稳定状态下基于DTW的毛羽H值周期模式识别算法,并使用局部暴力搜索和剪枝方法对识别算法进行优化。
1 毛羽H值周期模式识别方法
1.1 动态时间规整算法
DTW是一个描述序列数据之间相似度和距离的函数,它可以求解两个序列匹配时的累计最小距离,同时可以衡量两个长短不一的序列。现有一组采集到的纱线毛羽数据,这组数据足够长,且在采集的过程中没有出现断纱等明显影响毛羽的因素。若按图1(a)所示的不同长度滑动窗口和欧几里得距离来提取毛羽H值的周期模式,最后得到的累加和最小的滑动窗口长度就是毛羽H值的周期。其中X是从原始毛羽数据中截取的一定长度序列(向量),然后和数据集中每一个相同长度滑动窗口中的片段序列Y1、Y2等进行欧几里得计算(见式(1)),最后计算它们的累加和。该方法默认周期模式特征分布在一个完全固定的长度和周期上,即相邻滑动窗口不重叠,X和Y1、Y2的长度相同。然而纱线是一种柔性的、纵向易于拉伸变形的物质,当受到自身不匀率和纵向拉力的影响时,其长度和毛羽特征分布会发生变化。因DTW可以规整两个不同长度的序列并计算相似度,基于DTW提取毛羽H值的周期模式,如图1(b)所示。
d(X,Y)=
(1)
式中:d为X和Y序列的欧几里得距离;xi和yi分别为X和Y序列上分布的毛羽特征值。

图1 两种毛羽H值周期模式提取方法Fig.1 Two methods of extracting cycle pattern of hairiness H-value
设Y是采集到的细纱工序纱线毛羽H值的原始数据集,X是从中提取的一段长度为N的序列,即X∈Y。T是分析计算得到的毛羽H值的理论周期,[T-t,T+t]是考虑生产实际和误差情况下毛羽H值可能存在的周期范围。为提取毛羽H值的周期模式,将Y拆解为[T-t,T+t]长度的序列,则Y={YT-t,…,YM,…,YT+t},其中YM={YM,1,…,YM,i,…}是包含所有长度为M的序列集合。任意一个序列YM,i与X的DTW计算如式(2)所示。通过计算找到距离最小、相似度最大的X序列,则其长度N为毛羽H值的实际周期,对应的序列为毛羽H值的周期模式。
为了对齐两个长度分别为N和M的纱线毛羽序列X和YM,i,DTW构建一个N×M的规整矩阵DN×M。矩阵中位置(i,j)上的矩阵元素D(i,j)代表(0,0)到(i,j)的最短距离平方和,则(N,M)位置上的元素值D(N,M)开平方即为两个序列间的DTW距离,计算公式[13-15]如下:
(2)
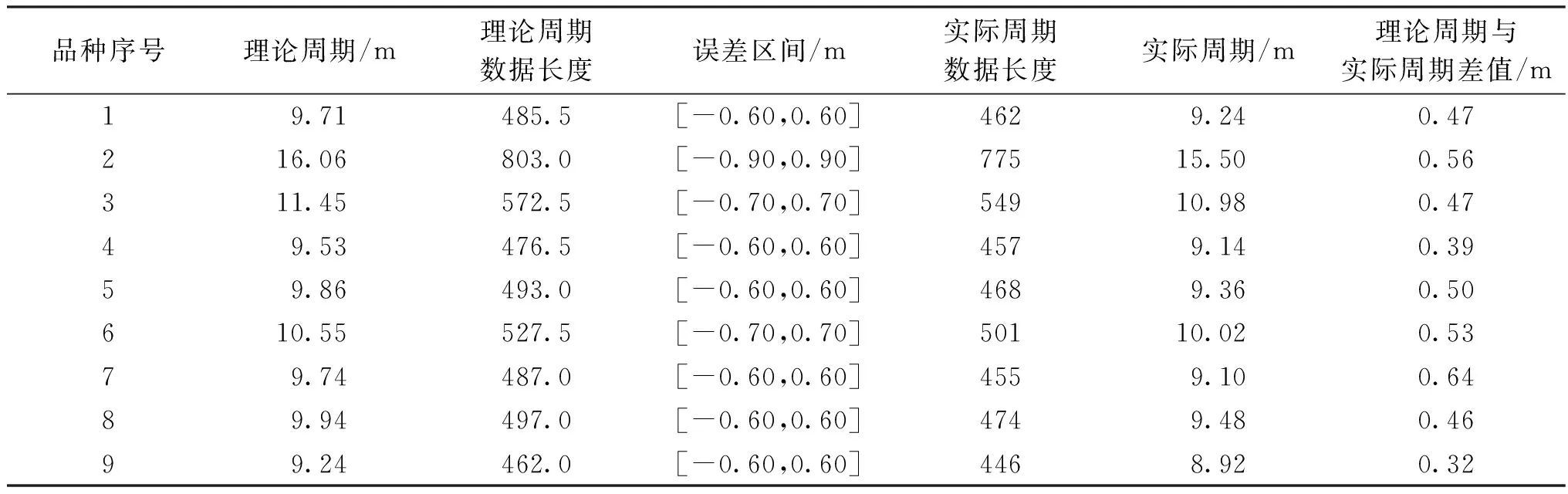
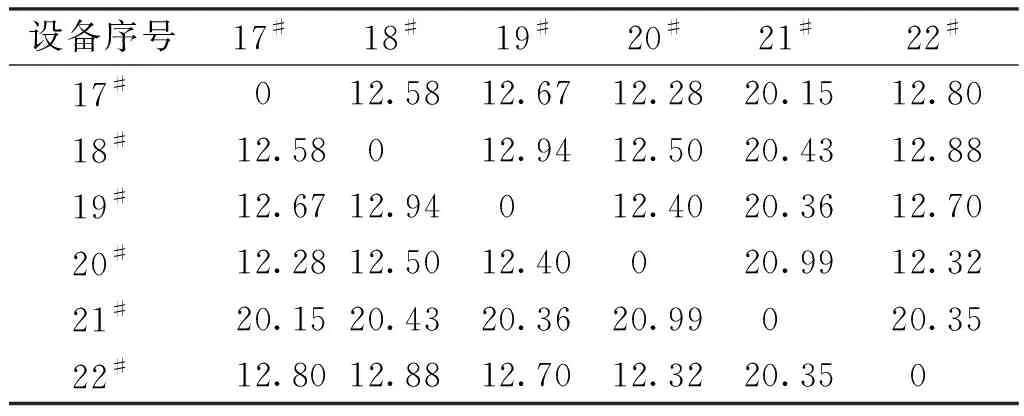
式中:w为规整矩阵DN×M中的路径点,wki和wkj分别为路径点的横、纵坐标,下标k代表第k步,同时也是规整矩阵DN×M中位置(0,0)到(N,M)规整路径的最后一步,满足max(N,M)≤k D(wki,wkj)=(X[wki]-YM,i[wkj])2+ D(w(k-1)i,w(k-1)j) (3) (4) D(0,0)=0,D(i,0)=∞,D(0,j)=∞ (5) 上述公式转化成的具体算法见算法1。其中:①是对规整矩阵进行初始化,如式(5)所示;②~④通过两层循环计算规整矩阵中每个位置上的元素值,如式(3)和(4)所示;⑤返回规整矩阵最后一个元素值的开平方,即两个序列数据的DTW距离度量值,如式(2)所示。 算法1原始的DTW算法 输入:毛羽H值数据集的任意一个序列YM,i以及从中提取的一段序列X 输出:YM,i和X的DTW距离 ①D(0,0) ← 0,D(0:len(X), 0) ← ∞,D(0, 0:len(YM,i)) ← ∞ ② fori←1 to len(X) do ③ forj←1 to len(YM,i) do ④D(i,j) = (X(i)-YM,i(j))2+ min(D(i-1,j-1),D(i,j-1),D(i-1,j)) 图2 两个具体序列的DTW距离计算图解[16]Fig.2 Illustration of the DTW distance calculation for two specific sequence [16] DTW算法的时间和空间复杂度为O(N×M),若对Y上所有长度在[T-t,T+t]区间的X候选集做1次搜索,将耗费巨大时间和空间成本。选用Y起始部分且长度为[T-t,T+t]的片段作为X候选集,即X候选集的样本个数为2t+1个。该步骤对算法的简化和性能提升可通过式(6)进行说明。 (6) 式中:d为改进前和改进后X候选集的数量之比,表示算法性能提升倍数;l为长度L的毛羽数据集上某个X候选片段的长度,且l∈[T-t,T+t];L-l+1表示长度为l的序列个数。由于t≪l≪L,d近似为L-T+1,甚至L。这充分说明减小搜索空间和减弱某特定长度序列的代表性可大幅提高运算效率。 在选定X候选集之后,对每个候选序列以[T-t,T+t]的滑动窗口确定该区域内最小DTW距离的YM,i片段,并以YM,i片段的终点为起点确定下一个[T-t,T+t]滑动窗口内最小DTW距离的片段。局部暴力搜索方法示意图如图3所示,即:候选集中某X先和[T-t,T+t]的滑动窗口中的2t+1个序列分别进行DTW计算,得到距离值最小且标号为Y1的片段,然后以Y1片段的终点作为起点设定下一个[T-t,T+t] 的滑动窗口即[L-t,L+t],在该区间内计算得到距离值最小且标号为Y2的片段;如此迭代直到达到Y的终点,计算得到X在Y上的DTW距离累加和,最后通过对比候选序列的结果得到实际的毛羽周期。在局部暴力搜索中,“局部”是指缩小搜索空间,如X候选集变为Y起始部分的2t+1个序列片段,而“暴力搜索”是指在这个已经缩小的局部搜索空间内计算X和YM,i所有组合的DTW距离。 图3 DTW局部暴力搜索方法Fig.3 Diagram of the DTW local violence search method 剪枝就是通过某种判断,避免一些不必要的遍历过程,常用于搜索算法的优化。应用剪枝优化的核心问题是设计剪枝判断方法,即确定哪些枝条应当舍弃,哪些枝条应当保留。利用剪枝方法进一步优化上述的局部暴力搜索,以提前结束迭代或搜索,算法流程如图4所示。该算法流程中主要包括两个循环体:一是用于遍历X候选集中的每个候选序列;二是用于计算Y上的所有周期序列和X的DTW距离累加和。添加剪枝操作在第二个循环体中,当某个X在Y上的DTW距离累加和大于当前最小的DTW距离累加和时结束当前循环,然后计算下个候选X。 根据图4所示的算法流程图实现的算法见算法2。其中:②~⑨对应算法的第一个循环体;④~⑦对应算法的第二个循环体;⑥~⑦对应算法第二个循环体中的剪枝操作。 算法2DTW暴力搜索和剪枝算法求解实际毛羽指标周期算法 输入:毛羽指标数据集Y,毛羽指标理论周期T,实际周期波动区间t 输出:实际毛羽指标周期TO ① min_sum=inf ② For eachXin {YT-t,0,…,YT,0,…,YT+t,0} ③ sum=0 ④ For eachYM,iinY ⑤ sum=sum+min(DTW(X,YM,i)) ⑥ if sum>min_sum ⑦ NextX ⑧ min_sum=sum ⑨TO=len(X) ⑩ returnTO 使用USTER TESTER 4-S型乌斯特条干仪作为检测设备。该仪器通过将电容极板间的电容量变化转换为电流变化,得到纱线的毛羽数据并绘制毛羽不匀率曲线。试样来自无锡经纬纺织公司的14台JWF1562EJM2型细纱机,试样生产环境温度为31~34 ℃。 研究棉纺细纱工序的纱线毛羽。为和其他混纺毛羽进行对比,采集不同品种的纱线试样进行试验,如表1所示。试验共采集9个品种的纱线试样,其中,重点研究的棉纺纱即品种1采集了110个纱线样本,其余品种均采集了20个纱线样本,最后通过试验平台对采集到的试样进行检测以获取相应的毛羽数据。 图4 剪枝算法流程图Fig.4 Flow diagram of pruning algorithm 表1 细纱纱线试样采集详情表Table 1 Details sheet of fine yarn specimens 寻找纱线毛羽H值的实际周期需要先确定各品种纱线毛羽H值的理论周期。在实际生产经验中认为钢领板上下往复的周期运动对毛羽的周期影响最大,因此,将钢领板的往复周期时间tg作为毛羽H值的理论周期指导。再考虑其他因素和纱线自身的影响,通过设定误差区间寻找毛羽H值实际的周期模式。纱线锭子的线速度为15~16 m/min。利用式(7)推导毛羽H值的理论周期T(m),其中锭子线速度取16 m/min作近似处理。 (7) 为准确得到生产各品种纱线时钢领板的往复周期,使用秒表重复多次测量周期时间并用平均值代替。其中,每个周期时间从钢领板到达上升的顶端开始计时,在再次达到上升的顶端时结束计时。最终测得的钢领板往复周期时间tg及毛羽H值的理论周期T如表2所示。 表2 钢领板往复周期和毛羽H值理论周期 表3 各品种纱线毛羽H值的实际周期试验结果Table 3 Experimental results of the actual cycle of the hairiness H-value for each yarn variety 在纺纱厂实际生产时,同一品种的纱线会由多台设备同时生产。按照相同的步骤重复了多台设备下品种1的实际周期试验,结果如表4所示。由表4可知,不同设备的毛羽H值实际周期略有差异,但非常接近。说明设备之间的差异带来了毛羽差异,但在相同的参数设定和一致的工况下不同设备生产的同品种纱线毛羽实际周期是非常接近的。图5为19#设备生产的纱线的毛羽H值周期模式示例。 表4 品种1在不同设备下生产的毛羽H值实际周期 不同设备生产的同一品种纱线的毛羽周期模式存在细微差异,故本文利用原始的DTW算法计算各周期模式间的DTW距离,得到的距离矩阵如表5所示。表5描述了来自不同设备同一品种纱线毛羽周期模式两两间的相关关系。文献[17]中,1台设备生产的试样的毛羽数据可以看作1个团,用作计算的是团内具有代表性的周期模式;表5则是对不同设备生产的试样的毛羽数据即团间进行相关性计算:因此可以依据相关性的强弱进行团间异常检测。由表5可知,除21#设备生产的试样外,其他设备生产的试样间的DTW距离约为12,而21#设备与其他设备生产的试样之间的距离约为20。观察发现21#设备生产的粗纱在该段沾染了污渍,导致毛羽H值异常。这表明通过周期模式对比可以检测异常情况[17],至于实际导致异常的原因则需进一步分析。 表5 同品种不同设备毛羽H值周期模式的DTW距离矩阵 针对细纱机各部件对纱线的周期性作用和纱线本身的特性,从毛羽数据出发研究提取周期模式的方法,提出使用滑动窗口和DTW方法提取纱线毛羽H值的周期模式,并使用局部暴力搜索和剪枝方法提升算法性能。研究发现:在1台设备上长期稳定生产的某品种纱线可采用同一毛羽周期模式进行描述;不同设备生产的同品种纱线的周期模式具有相似性;当某设备生产的纱线的毛羽周期模式在DTW距离矩阵中出现不同于其他周期模式的现象时,可能存在某种异常或故障;优化后的DTW算法可根据近似卷绕速度和设定误差区间得到最终的毛羽H值理论周期,从而反向推导出实际的卷绕速度。除品种2的钢领板上下往复周期为60.23 s外,其余约为36 s,而国产钢丝圈的使用寿命约为15 d,这个往复周期和使用寿命可分别代表纱线毛羽的短期周期和长期趋势。下一步将基于毛羽H值的短期周期和钢丝圈导致的长期趋势进行联合预测以提高算法的预测精度。
i=1,2,…,N;j=1,2,…,M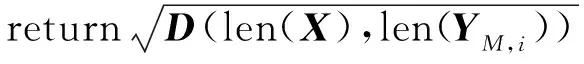
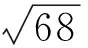
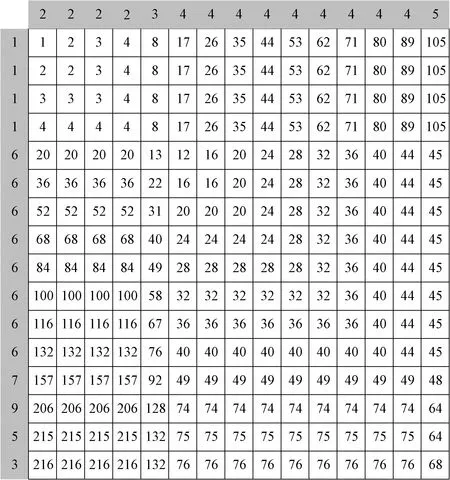
1.2 局部暴力搜索和剪枝算法

2 试验过程
2.1 试验平台
2.2 试验方法

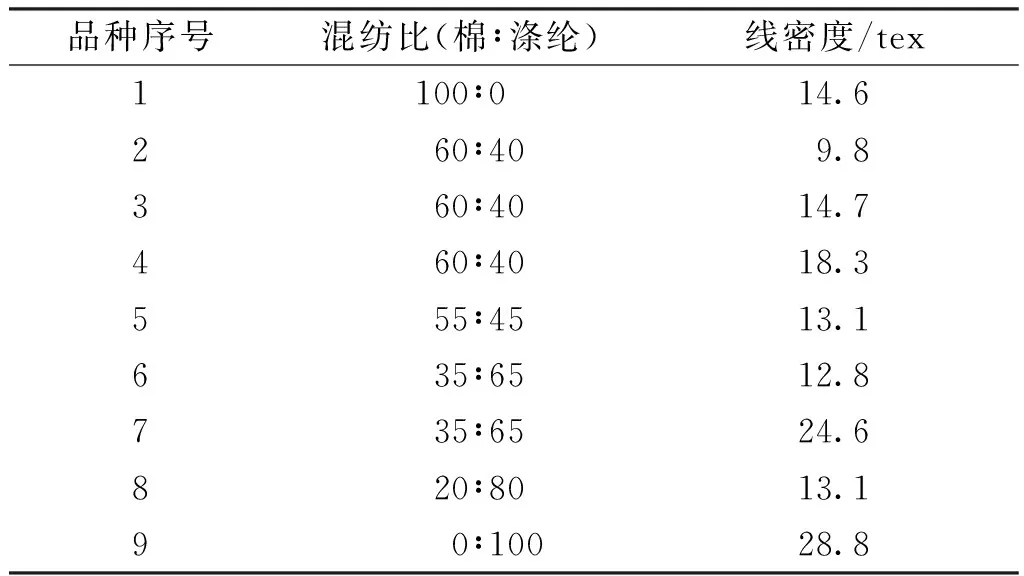

2.3 试验结果分析
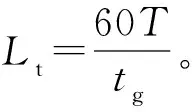

3 结 语
