Convergence in Conformal Field Theory
2022-12-06YiZhiHUANG
Yi-Zhi HUANG
Abstract Convergence and analytic extension are of fundamental importance in the mathematical construction and study of conformal field theory.The author reviews some main convergence results,conjectures and problems in the construction and study of conformal field theories using the representation theory of vertex operator algebras.He also reviews the related analytic extension results,conjectures and problems.He discusses the convergence and analytic extensions of products of intertwining operators(chiral conformal fields)and of q-traces and pseudo-q-traces of products of intertwining operators.He also discusses the convergence results related to the sewing operation and the determinant line bundle and a higher-genus convergence result.He then explains conjectures and problems on the convergence and analytic extensions in orbifold conformal field theory and in the cohomology theory of vertex operator algebras.
Keywords Conformal field theory,Vertex operator algebras,Representation theory,Convergence,Analytic extension
1 Introduction
Quantum filed theory has become an important area in mathematics.Many mathematical problems are deeply connected to structures studied in quantum field theory and have been solved or are expected to be solved using the ideas and tools developed in the mathematical study of quantum field theory.
The most successful quantum field theories are topological ones.Since the state spaces of these quantum field theories are typically finite dimensional,topological field theories usually do not involve convergence problems.On the other hand,since the state spaces of nontopological quantum field theories must be infinite dimensional,convergence problems are often the most basic ones that we have to solve first.For topological quantum field theories that are constructed using some underlying nontopological quantum field theories,one might also need to solve some convergence problems.Such convergence problems are in fact problems for the underlying nontopological quantum field theories.
Convergence results and problems in mathematics are usually related to existence results and problems.Such existence results and problems are always of fundamental importance in mathematics.For example,the first fundamental problem for a differential equation is the existence of solutions under suitable conditions.Though one can still derive many important results by assuming the existence of a mathematical structure,such results in mathematics are still conjectures unless the existence is proved.In a problem related to analysis,the existence is often a problem about convergence.For example,the existence of a solution of a differential equation is mostly a problem about the convergence of a sequences of functions obtained from a suitable iteration procedure.In some cases,even though the further development of a problem was studied using algebraic methods,without the existence established by proving suitable convergence results,the subsequent important results would still be conjectures.
One main nontopological conformal field theory for which we have precise definitions and substantial mathematical results is two-dimensional conformal field theory.In this paper,for simplicity,we shall omit the words “two-dimensional” so that by conformal field theory,we always mean two-dimensional conformal field theory.Conformal field theory was studied in physics using the approach of operator product expansion starting from the work of Belavin-Polyakov-Zamolodchikov[3].The fundamental early works of Friedan-Shenker[12],Verlinde[39],Moore-Seiberg[35]and others led to some major conjectures on rational conformal field theories.Around the same time,the representation theory of vertex operator algebras was developed starting from the works of Borcherds[4]and Frenkel-Lepowsky-Meurman[11].The representation theory of vertex operator algebras is now one of the main mathematical approaches for the construction and study of conformal field theory.
In the construction and study of conformal field theories using the representation theory of vertex operator algebras,almost in every major step,we have to prove a convergence result.Moreover,these convergence results are always obtained together with some analytic extension results that are necessary and important for proving further results on conformal field theories.To further develop conformal field theory and apply conformal field theory to solve mathematical problems,many convergence and analytic extension conjectures and problems still need to be proved and solved.Without the proofs of these conjectures and the solutions to these problems,we would not and will not be able to solve many of the mathematical problems related to conformal field theory.
In this paper,we review some main convergence results,conjectures and problems in the construction and study of two-dimensional conformal field theories using the representation theory of vertex operator algebras.We also discuss the related analytic extension results,conjectures and problems.These analytic results and problems are of the fundamental importance in the study of conformal field theory and the representation theory of vertex operator algebras.We believe that in the future study and applications of conformal field theory,the results and problems on convergence and analytic extensions will play an even more important role.
For the definitions and basic properties of vertex operator algebras,(lower-bounded and grading-restricted)generalized V-modules and(logarithmic)intertwining operators,see for example,[10,24,26].For simplicity,in this paper,we shall call a logarithmic intertwining operator an intertwining operator.
This paper is organized as follows:In Section 2,as a comparison with the main convergence results that we shall discuss in later sections,we discuss the convergence of products of vertex operators for vertex operator algebras and modules.We also briefly discuss the generalizations this type of convergence in this section.In Sections 3—4,we discuss the convergence and analytic extensions of products of intertwining operators and the convergence and analytic extensions of q-traces and pseudo-q-traces of products of intertwining operators,respectively.In Section 5,we discuss the convergence related to the sewing operation of spheres with punctures and local coordinates vanishing at the punctures and to the determinant line bundle.In Section 6,a higher-genus convergence result proved by Gui is discussed.The convergence and analytic extension conjectures and problems in orbifold conformal field theory and the convergence problems in the cohomology theory of vertex operator algebras are discussed in Sections 6 and 7,respectively.
2 Rational Functions,Their Generalizations and Algebraic Convergence
The convergence of an expansion of a rational functions(or suitable simple generalizations of rational functions)is the simplest type of convergence appearing in the study of vertex operator algebras,their modules and twisted modules.This type of convergence is simple,algebraic and very useful,but unfortunately does not work for general intertwining operators.We begin our discussion of the convergence in this paper with this type of convergence and the reader should compare it with the convergence to be discussed in later sections.

where g(z1,z2)∈C[z1,z2]and m,n,l∈N.In other words,h(z1,z2)is absolutely convergent in the region|z1|>|z2|>0 to the rational function f(z1,z2).The rational function f(z1,z2)is an analytic function defined on the regionand thus is the analytic extension to M2of the sum of h(z1,z2)on the region|z1|>|z2|>0.
This simple fact gives a method to prove the convergence of a suitable series h(z1,z2)∈To prove this convergence,we need only find a nonnegative integer N such that(z1−z2)Nh(z1,z2)is a Laurent polynomial in z1and z2.Note that the algebraic formulation of this convergence holds when we replace C by any field F of characteristic 0.


where(z1−z2)Nis understood as the binomial expansion of(z1−z2)Nin nonnegative powers of z2,that is,the expansion of(z1−z2)Nin the region|z1|>|z2|>0.Then the same argument as above shows that h(z1,z2)is equal to the expansion as a series in powers of z1and z2with only finitely many negative real parts of the powers of z2of a function

where g(z1,z2)∈C[z1,z2],m,n∈N and l∈C.In other words,h(z1,z2)evaluated using any values,log z1and log z2is absolutely convergent in the region|z1|>|z2|>0 to the function f(z1,z2)evaluated using the same values.But in practice,it is not easy to apply this method in this general case since the generalization of the weak commutativity in this case is not easy to verify.In fact,since the power N is not a nonnegative integer anymore,the expansion of(z1− z2)Nin the regions|z1|>|z2|>0 and|z2|>|z1|>0 are very different.In this case,the weak commutativity for two(multivalued)fields A1(z1)and A2(z2)is of the form
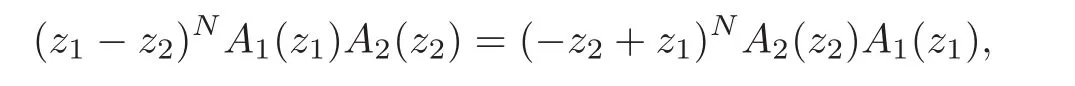
where(z1−z2)Nis the binomial expansion of(z1−z2)Nin nonnegative powers of z2and(−z2+z1)Nis the binomial expansion of(−z2+z1)Nin nonnegative powers of z1.In general,this weak commutativity is not always easy to verify since(z1−z2)Nand(−z2+z1)Nare very different.
For general intertwining operators(for example,intertwining operators among modules for the affine vertex operator algebras and Virasoro vertex operator algebras),even weak commutativity for abelian intertwining operator algebras is not satisfied.This is the main reason why we need the method in the next section to prove the convergence of products of intertwining operators.Even in some special cases that we expect the intertwining operators to form an abelian intertwining operator algebra,because of the difficulty to verify the weak commutativity mentioned above,we still need the method in the next section to prove the convergence of products of intertwining operators.
Our discussions above are for series in only two complex variables or products of two series of operators.But they can be generalized easily to the case of an arbitrary number of complex variables or products of an arbitrary number of series of operators.
3 Convergence of Products of Intertwining Operators
The convergence discussed in the preceding section does not work for general intertwining operators.We have to use a completely different method.In this section,we discuss the convergence of products of intertwining operators and their analytic extensions using this method.

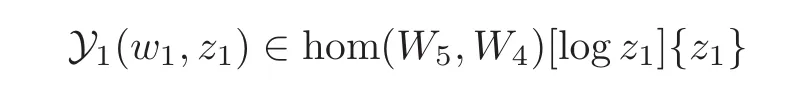

The first problem in the study of the product Y1(w1,z1)Y1(w2,z2)is the convergence of this product in a suitable sense.Since the series Y1(w1,z1)Y1(w2,z2)contains nonintegral powers of z1and z2and nonnegative integral powers of log z1and log z2,we first need to choose values of these powers of z1and z2and values of log z1and log z2.In fact,if the values of log z1and log z2are chosen to be lp(z1)=log|z1|+i arg z1+2πip and lq(z2)=log|z2|+i arg z2+2πiq,where 0 ≤ arg z1,arg z2<2π,then these values also give values emlp(z1)and enlq(z2)of the powersof z1and z2.Using these values,we obtain a series in C,

for w1∈W1,w2∈W2,w3∈W3and w′4∈W′4.We want to know whether(3.1)is absolutely convergent in a suitable region for z1and z2.
In general,(3.1)might not be convergent.The method used in the preceding section works only when it is possible to multiply a nonnegative integral powers(z1−z2)Nof z1−z2to get a finite sum.But in general(even in the case of abelian intertwining operator algebras),there is no such N;in general,there is even no polynomial in z1and z2that can be multiplied to(3.1)to get a finite sum.
The method used to prove the convergence of(3.1)is to show that the series(3.1)satisfies the expansion in the region|z1|>|z2|>0 of a system of differential equations with coefficients in the ring

and with regular singular points at(z1,z2)=(∞,0).In fact,since each coefficient of(3.1)as a series in powers of z2and log z2is a finite sum,we need only prove the convergence of(3.1)for fixed z1∈ C×.In particular,we need only derive a differential equation in the variable z2with the regular singular point z2=0.Then by the theory of differential equations of regular singular points,the formal series solution of the system of the differential equations of regular singular points must be the expansion of an analytic solution of the system.In other words,the series(3.1)is absolutely convergent in the region|z1|>|z2|>0 to an analytic solution.Since the coefficients of the system of differential equations are in the ring R,this solution on the region|z1|>|z2|>0 can be analytically extended to a multivalued analytic function on M2.Moreover,this multivalued analytic extension also satisfies a system of differential equations with coefficients in R and with regular singular points at(z2,z1− z2)=(∞,0).Then the multivalued analytic extension can be expanded in the region|z1|>|z1−z2|>0 as a series containing terms in powers of z2and z1−z2and nonnegative integral powers of logarithms of z1and z2.
In the special case of Wess-Zumino-Witten models or minimal models,we have the Knizhnik-Zamolodchikov equations(see[30])or the Belevin-Polyakov-Zamolodchikov equations(see[3]),respectively.The Knizhnik-Zamolodchikov equations were used by Tsuchiya and Kanie[38]to prove the convergence of products of intertwining operators(called vertex operators in[38])among suitable modules for the affine Lie algebra.The Belevin-Polyakov-Zamolodchikov equations and Knizhnik-Zamolodchikov equations were used by the author[14]and by Lepowsky and the author[25],respectively,to prove the convergence of products of intertwining operators for vertex operator algebras for the minimal models and for the Wess-Zumino-Witten models.But for general vertex operator algebras,products of intertwining operators might not satisfy differential equations.Some conditions on the vertex operator algebras and modules must be satisfied in order to have such differential equations.
Using the Jacobi identity for intertwining operators and vertex operators acting on modules,we obtain certain identities for series of the form(3.1).For example,we have

where(Resxx−1−kYW2(u,x))′is the adjoint on W′4of Resxx−1−kYW4(u,x).Using these identities,the C1-cofiniteess condition,the quasi-finite-dimensionality of the generalized V-modules involved and the L(−1)-derivative property,it was proved in[17]that the derivatives of(3.1)span a finitely-generated module over R and thus must satisfy the expansion in the region|z1|>|z2|>0 of a system of differential equations with coefficients in R.Using more careful examinations of the coefficients of the differential equations,it was proved in[17]that one can always find such a system of differential equations such that the singular point(z1,z2)=(∞,0)or(z2,z1−z2)=(∞,0)is regular.(As is mentioned above,in fact it is enough to show that for fixed z1∈ C×,(3.1)satisfies a differential equation in the variable z2with the regular singular point z2=0.)Then we obtain the convergence and analytic extension result for products of two intertwining operators.
Below is the precise statement of the convergence and analytic extension result.It is essentially the n=2 case of[28,Theorem 11.8]with the category C being the category of gradingrestricted generalized V-modules.Its proof was in fact given in the proof of[17,Theorem 3.5],where it is proved in addition that when all N-gradable weak V-modules are completely reducible,there is no logarithms of the variables in the expansion near the singular point(z2,z1− z2)=(∞,0).

The convergence and analytic extensions of products of more than two intertwining operators are proved similarly.The convergence and analytic extensions of iterates of intertwining operators can be derived from Theorem 3.1 and properties of intertwining operators.See[27—28].
4 Convergence of q-Traces and Pseudo-q-Traces of Products of Intertwining Operators
The multivalued analytic functions obtained from the analytic extensions of products of intertwining operators discussed in the preceding section are in fact the genus-zero correlation functions for the corresponding chiral conformal field theories.To construct genus-one correlation functions from these genus-zero correlation functions,we need to take q-traces and pseudo-q-traces of products of intertwining operators.Since grading-restricted generalized V-modules in general are always infinite dimensional,the first problem one needs to solve is the convergence of these q-traces and pseudo-q-traces.
As in the case of products of intertwining operators,we shall discuss only the case of q-traces and pseudo-q-traces of products of two intertwining operators.The general case is similar.
Geometrically,products of intertwining operators correspond to genus-zero Riemann surfaces with punctures and local coordinates(see[15—16])but the q-traces or pseudo-q-traces of products of intertwining operators correspond to genus-one surfaces with punctures and local coordinates.Since the standard description of genus-one Riemann surfaces is in terms of parallelograms in the complex plane,not annuli in the sphere,to use intertwining operators to write down genus-one correlation functions,we have to modify intertwining operators correspondingly.
For a grading-restricted generalized V-module W,as in[18],let



commute with the action of P on W3.Note that the q-trace(4.1)is the special case of(4.2)for which P={e},where e is the identity element of P,and φ is given by φ(e)=1.We want to know whether(4.1)and(4.2)are absolutely convergent in a suitable region for z1,z2and q.
In general,(4.1)—(4.2)might not be convergent.Just as in the case of products of intertwining operators,we also need some cofiniteness condition.When the confiniteness condition is satisfied,(4.1)—(4.2)are convergent in a suitable region.The method that we use to prove this convergence is to show that the series(4.1)—(4.2)satisfy the expansion in the region 1>|qz1|>|qz2|>|q|>0 of a system of differential equations with coefficients in the ring C[G4(τ),G6(τ),℘2(z1− z2;τ),℘3(z1− z2;τ)],where
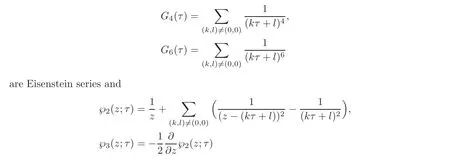
are Weierstrass℘-function and its derivative with respect to z multiplied by−.
The first convergence result on q-traces of products of vertex operators on a V-module was obtained by Zhu[41]for V satisfying the conditions that V has no nonzero element of negative weights,every lower-bounded generalized V-module is completely reducible and a cofiniteness condition which is now called the C2-cofiniteness condition.Let C2(V)be the subspace of V spanned by elements of the form Resxx−2YV(u,v)v for u,v∈V.If dim V/C2(V)< ∞,we say that V is C2-cofinite.The convergence result of Zhu was generalized by Miyamoto in[33]to a convergence result on q-traces of products of one intertwining operator and several vertex operators on modules in the case that V satisfies the three conditions mentioned above in Zhu’s paper[41].It was also generalized by Miyamoto in[34]to a convergence result on pseudoq-traces of products of vertex operators on a V-module in the case that V has no nonzero element of negative weights and is C2-cofinite.These convergence results are all proved in two steps:(i)An algebraic recurrence relation is proved to reduce the convergence of(pseudo-)qtraces of products of n vertex operators on a V-module(or products of n−1 vertex operators on a V-module and one intertwining operator)to the convergence of(pseudo-)q-traces of one vertex operator(or one intertwining operator)on the same V-module.(ii)The convergence of(pseudo-)q-traces of one vertex operator(or one intertwining operator)on the same V-module is proved by using differential equations of regular singular points.
The proofs of the algebraic recurrence relations in step(i)above need the commutator formula for vertex operators on V-modules or the commutator formula between vertex operators on V-modules and intertwining operators.Since in general there is no commutator formula for intertwining operators,there is no algebraic recurrence relation to reduce the convergence of(4.1)—(4.2)to the convergence of(pseudo-)q-traces of intertwining operators.This difficulty is the main reason why the modular invariance of the space of q-traces of products of at least two intertwining operators had been a conjecture for many years after Zhu’s work[41].
In[18],the author proved the convergence of(4.1).In[8—9],using the same method,Fiordalisi generalized the convergence of(4.1)proved in[18]to the convergence of(4.2).In fact,certain formulas on q-traces of products of geometrically-modified intertwining operators are proved in[18]and generalized in[8—9]to pseudo-q-traces of products of geometrically-modified intertwining operators.For example,one such formula is
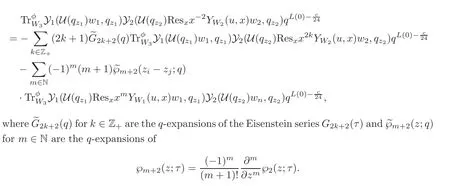

Below is the precise statement of the convergence and analytic extension of(4.2).As is mentioned above,(4.1)is a special case of(4.2).In the semisimple case that every lowerbounded generalized V-module is completely reducible,(4.2)is the same as(4.1).
Theorem 4.1(see[8—9,18])Assume that the vertex operator algebra V has no nonzero element of negative weights and is C2-cofinite.Then in the region 1>|qz1|>|qz2|>|qτ|>0,the series(4.2)with q=qτ=e2πiτis absolutely convergent and can be analytically extended to a multivalued analytic function in the region given by ℑ(τ)>0(here ℑ(τ)is the imaginary part of τ),z1/=z2+kτ+l for k,l∈ Z.Moreover,the singular point z1=z2+kτ+l for each k,l∈Z is regular,that is,any branch of the multivalued analytic function can be expanded in a neighborhood of the singular point z1=z2+kτ+l as a series of the form
where rj∈ R for j=1,···,M and fj,p(z)for j=1,···,M,p=0,···,K are analytic functions on a disk containing 0.
The convergence and analytic extensions of q-traces and pseudo-q-traces of products of more than two intertwining operators are proved similarly.See[8—9,18].
5 Convergence Results Associated to the Sewing Operations of Genus-Zero Riemann Surfaces and Determinant Lines
Vertex operator algebras have a geometric definition in terms of the partial operad of the moduli space of suitable genus-zero Riemann surfaces with punctures and local coordinates and the determinant line bundle over this moduli space,see[15].To prove that a vertex operator algebra V indeed satisfies this geometric definition,associated to such surfaces,we need to construct suitable linear maps from tensor powers of V to the algebraic completion of V using vertex operators(corresponding to spheres with three punctures and standard local coordinates)and Virasoro operators(corresponding to spheres with two punctures and local coordinates).The main work is to prove that these linear maps satisfy some basic properties,including a sewing axiom.Since there are conformal anomalies(corresponding to central charges for the Virasoro operators),the determinant line bundle over the moduli space of such Riemann surfaces and its powers are also involved.
The convergence results discussed in the preceding three sections are for the constructions of correlation functions associated to genus-zero or genus-one Riemann surfaces with punctures and standard local coordinates vanishing at the punctures.To construct and study correlation functions associated to Riemann surfaces with punctures and general local coordinates vanishing at the punctures,we need to exponentiate suitable infinite sums of Virasoro operators and prove that they behave exactly in the same way as the underlying surfaces and determinant lines.The properties that one has to prove include in particular a convergence involving the exponentials of suitable infinite sums of the Virasoro operators and another convergence involving the central charge of the Virasoro algebra.These convergence problems related to the Virasoro operators were solved by the author in[15].
For simplicity,we use genus-zero Riemann surfaces with only two punctures(one positively oriented and the other negatively oriented)and local coordinates vanishing at the punctures to describe these convergence results.Such a Riemann surface with punctures and local coordinates is conformally equivalent to C∪{∞}with the positively oriented puncture 0 and negatively oriented puncture∞.Then the local coordinate vanishing at 0 becomes a univalent analytic function f0(w)defined near 0 and vanishing at 0.Similarly the local coordinate vanishing at∞ becomes a univalent analytic function f∞(w)defined near∞ and vanishing at∞.It is further conformally equivalent to C∪{∞}with punctures 0 and∞ and with local coordinates given by f0(w)and f∞(w)as above such that the Laurent expansion of f∞(w)is of the form1w+ ···,where ···are higher order terms in.We denote C ∪ {∞}with such punctures and local coordinates by Σ.Such a genus-zero Riemann surface with two punctures and local coordinates vanishing at the punctures are said to be canonical.
Let[Σ]be the conformal equivalence class of a canonical genus-zero Riemann surface Σ with two punctures and local coordinates vanishing at the punctures.As in[15],we have


respectively.Then we have ν[Σ1],ν[Σ2]:.We define a series ν[Σ1]◦ ν[Σ2]of linear maps from V toby

On the other hand,if there exists r ∈ R+such that we can cut disks of radius r from Σ1and Σ2using the local coordinates vanishing at 0 on Σ1and at ∞ on Σ2,respectively,with the remaining parts of the surfaces still containing the other punctures,we say that Σ1can be sewn with Σ2.In this case,we identify the boundary of the remaining part of Σ1with the boundary of the remaining part of Σ2using the composition of the local coordinate map near 0 in Σ1,the mapand the inverse of the local coordinate map near ∞ in Σ2to obtain a new genus-zero Riemann surfaces with two punctures and local coordinates.We denote it by Σ11∞0Σ2.The sewing axiom in the geometric definition of vertex operator algebra states that ν[Σ1]◦ ν[Σ2]is absolutely convergent when Σ1can be sewn with Σ2and its sum is proportional to ν[Σ11∞0Σ2].
To prove the sewing axiom in this case,one first has to prove the convergence of ν[Σ1]◦ ν[Σ2]when Σ1and Σ2can be sewn together.The following result is a special case of a more general result proved in[15].
Theorem 5.1(see[15])Assume that Σ1can be sewn with Σ2.Then ν[Σ1]◦ν[Σ2]is absolutely convergent in the sense that for v ∈ V and v′∈ V′,

where the right-hand side should be viewed as a Laurent series in a0.It is proved in[15]by using formal calculus and properties of the Virasoro operators on V that the right-hand side of(5.1)is equal to
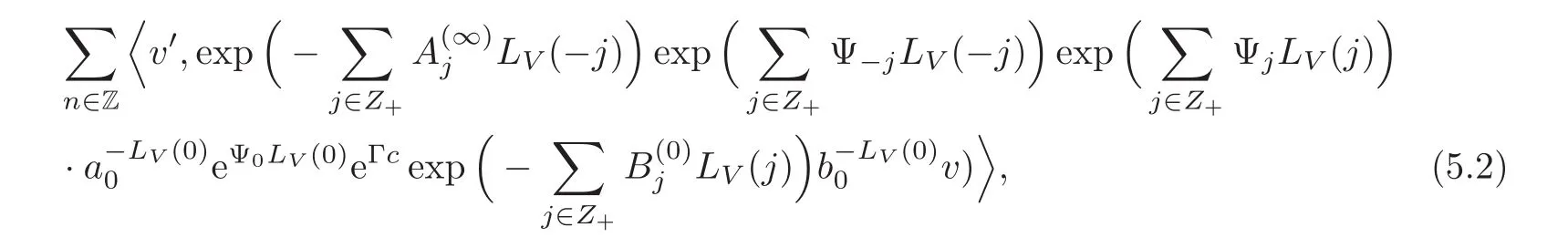
where Ψjfor j ∈ Z and Γ are Laurent series inwith polynomials infor j∈ Z+as coefficients.It is proved in[15]by using the uniformization theorem and an old result of Grauert that the Laurent series Ψjfor j∈ Z are expansions of analytic functions and therefore are absolutely convergent.It is also proved in[15]by using the analyticity of the canonical isomorphisms between the tensor product of the determinant lines of Σ1and Σ2and the determinant line of Σ11∞0Σ2,that the Laurent series Γ is the expansion of an analytic function and therefore is also absolutely convergent.Then(5.2)and thus the left-hand side of(5.1)is absolutely convergent.
The convergence result discussed above also applies to lower-bounded generalized V-modules and even to any lower-bounded graded modules for the Virasoro algebra.
The convergence of Ψjfor j ∈ Z above was generalized by Barron[1—2]to the case of N=1 superconformal algebras.
6 A Higher-Genus Convergence Result of Gui
Conformal field theories have a geometric formulation given by Segal[37].Segal in[37]further gave a geometric formulation of chiral conformal field theories(called weakly conformal field theories).One of the main goal of the mathematical study of conformal field theories is to construct chiral and full conformal field theories satisfying Segal’s axioms.In particular,one needs to construct correlation functions associated to Riemann surfaces with ordered,parametrized and labeled boundaries or,equivalently,Riemann surfaces with punctures and local coordinates vanishing at punctures,from genus-zero Riemann surfaces with one,two or three punctures and local coordinates.Correlation functions corresponding to the genus-zero Riemann surface with one puncture and the standard local coordinate are determined by the vacuum of the conformal field theory.Correlation functions corresponding to genus-zero Riemann surfaces with two punctures and local coordinates have been discussed in the preceding section and are given by the Virasoro operators on modules for a vertex operator algebra.Correlation functions corresponding to genus-zero Riemann surfaces with three punctures and standard local coordinates are given by intertwining operators.So to construct chiral conformal field theories,one needs to construct correlation functions associated to arbitrary Riemann surfaces with punctures and local coordinates from the vacuum,the Virasoro operators and intertwining operators.The genus-zero correlation functions and genus-one correlation functions were constructed in[17]and[18],respectively(see also Sections 3—4 for the convergence problems associated to these constructions).
To construct higher-genus chiral correlation functions from genus-zero and genus-one chiral correlation functions,we need to prove a higher-genus convergence.For rational conformal field theories,this was in fact stated as a conjecture in[21,40].This conjecture was proved in 2020 by Gui[13].
We now describe this higher-genus convergence result.Let W1,···,Wnbe grading-restricted generalized V-modules.For w1∈ W1,···,wn∈ Wn,an n-point genus-g correlation function associated to W1,···,Wnis a linear map from W1⊗ ···⊗ Wnto the space of multivalued analytic functions on the moduli space of genus-g Riemann surfaces with n punctures and local coordinates vanishing at the punctures satisfying suitable conditions.Here for simplicity we omit the description of these conditions.
Let Σ1be a genus-g1Riemann surface with n1punctures and local coordinates vanishing at the punctures and Σ2be a genus-g2Riemann surface with n2punctures and local coordinates vanishing at the punctures.If there exists r∈R+such that we can cut disks of radius r from Σ1and Σ2using the local coordinates vanishing at the i-th puncture on Σ1and at the j-th puncture on Σ2,respectively,with the remaining parts of the surfaces still containing the other punctures,we say that Σ1can be sewn with Σ2at the i-th puncture on Σ1and the j-th puncture on Σ2.In this case,we can identify the boundary of the remaining part of Σ1with the boundary of the remaining part of Σ2using the composition of the local coordinate map near the i-th puncture on Σ1,the mapand the inverse of the local coordinate map near the j-th puncture on Σ2to obatin a new Riemann surfaces with punctures and local coordinates.
Let ψ1be an n1-point genus-g1correlation function associated to W1,···,Wn1and ψ2be an n2-point genus-g2-correlation function associated to.Assume thatOne axiom for chiral conformal field theories requires that the series

is absolutely convergent when Σ1can be sewn with Σ2at the i-th puncture on Σ1and the j-th puncture on Σ2,whereare dual homogeneous basis of Wiand.This is the higher-genus convergence problem for the sewing of two Riemann surfaces.The convergence of products of intertwining operators discussed in Section 3 is the special case of this convergence.
There is also another convergence problem for the self sewing of one Riemann surface.Let Σ be a genus-g Riemann surface with n punctures and local coordinates vanishing at punctures.If there exists r ∈ R+such that we can cut disks of radius r from Σ using the local coordinates vanishing at the i-th and the j-th punctures on Σ with the remaining parts of the surfaces still containing the other punctures,we say that Σ can be sewn at the i-th and j-th punctures.In this case,we can also obtain a new genus-g+1 Riemann surface with n−2 punctures and local coordinates vanishing at the punctures by sewing Σ at the i-th and j-th punctures using the same procedure as in the case of two surfaces above.
Let ψ be an n-point genus-g correlation function associated to W1,···,Wn.Assume that.Assume that i is absolutely convergent when Σ can be sewn at the i-th and j-th punctures.This is the convergence problem for the self sewing of one Riemann surface.The convergence of the qtraces of products of geometrically-modified intertwining operators discussed in Section 4 is the special case of this convergence. The following theorem is proved by Gui in[13]. Theorem 6.1(see[13]) Let V be a C2-cofinite vertex operator algebra containing no nonzero elements of negative weights.If the grading-restricted generalized V-modules involved are finitely generated,then(6.1)–(6.2)are absolutely convergent when Σ1can be sewn with Σ2at the i-th puncture on Σ1and the j-th puncture on Σ2and when Σ can be sewn at the i-th and j-th punctures,respectively. As in the proof of the convergence of products of intertwining operators and the proof of the convergence of q-traces and pseudo-q-traces of products of geometrically-modified intertwining operators discussed Sections 3 and 4,respectively,this theorem is proved in[13]by deriving differential equations.But in this case the derivation of the differential equations involving analytic functions on the moduli space of higher-genus Riemann surfaces.These analytic functions are much more difficult to study than those on the moduli spaces of genus-zero and genus-one Riemann surfaces.For example,the differential equations satisfied by q-traces and pseudo-q-traces of products of intertwining operators were derived using the q-expansions of the derivatives of the Weierstrass function(see[18]).We need similar results for functions on the moduli space of higher-genus surfaces.This difficult in the higher-genus case was overcame in[13]by using a theorem of Grauert in complex analysis. Orbifold conformal field theories are conformal field theories constructed from known conformal field theories and their automorphisms.In the framework of the representation theory of vertex operator algebras,orbifold conformal field theory is the study of twisted intertwining operators among(generalized)twisted modules.In this section,we discuss the convergence conjectures and problems for orbifold conformal field theories. satisfying suitable axioms,including in particular an equivariance property and a duality property which requires that products of twisted vertex operators are convergent in suitable regions and the associativity and commutativity for twisted intertwining operators hold.To construct lower-bounded generalized twisted modules,the convergence of products of twisted vertex operators can be proved using the method in Section 2(see[22]).In[7],by using the method of Zhu[41],Dong,Li and Mason generalized the convergence and analytic extension results of Zhu[41]to the convergence and analytic extension of q-traces of twisted vertex operators on a g-twisted module associated to a finite order automorphism g of a C2-cofinite vertex operator algebra V.But orbifold conformal field theories are about twisted intertwining operators among twisted modules.In general,the convergences of products and(pseudo-)q-traces of products of twisted intertwining operators are still conjectures. But for an infinite group or a finite nonsolvable group G,VGbeing C2-cofinite or even C1-cofinite when V is C2-cofinite is still an open problem.Instead of trying to prove VGsatisfies the conditions needed,the author proposed in[21,23]a program to study orbifold conformal field theories by studying directly twisted intertwining operators among suitable generalized twisted V-modules.In this program,we need to prove in particular that(7.1)is absolutely convergent in the region|z1|>|z2|>0 and the sum can be analytic extended as in Theorem 3.1.As in the case of intertwining operators among(untwisted)generalized V-modules,we expect that(7.1)is absolutely convergent only when W1,W2,W3,W4and W5as generalized twisted V-modules(not as generalized VG-modules)satisfy certain conditions. Though(7.1)looks completely the same as(3.1),it is much more difficult to study since the twisted vertex operators for generalized twisted modules in general involve nonintegral powers and logarithms of the variables.It is especially difficult to study in the case that the automorphisms g1,g2,g3,g4,g5do not commute with each other.There is still no general convergence result yet.But we have the following conjecture formulated in[21,23]. The general form of this convergence conjecture is for pseudo-q-traces of products of more than two intertwining operators.See[23]for details. In the general case,we have the following problem. Problem 7.1 Let V be a vertex operator algebra and let G be a group of automorphisms of V.Under what conditions do products and pseudo-q-traces of products of twisted intertwining operators among the grading-restricted generalized g-twisted V-modules for g∈G converge and have analytic extensions as in the conjectures above? Since cochains in this cohomology theory by definition must satisfy such a convergence condition,results and explicit calculations in this cohomology theory are always based on some basic convergence results or assumptions.Though the series involved should be convergent to rational functions,the method in Section 2 cannot be applied because cochains does not satisfy properties such as weak commutativity or weak associativity.To understand this cohomology theory and apply it to solve mathematical problems,we need to find algebraic conditions on the vertex algebra and modules and to develop new techniques to prove this type of convergence under these algebraic conditions. It is proved in[19]that 1-cochains always satisfy the convergence condition.So here we use 2-cochain to discuss the convergence condition.Given a grading-restricted vertex algebra V and a grading-restricted(or lower-bounded)generalized V-module W,a 2-cochain composable with m vertex operators is equivalent to a linear map satisfying certain conditions,including in particular,the condition that the series obtained from the compositions of Ψ with m vertex operators are absolutely convergent in suitable regions. For example,for w′∈ W′,v,v1,···,vk+l+1∈ V, should be absolutely convergent in the region|z1|> ···|zk|>|z|>|zk+1|> ···>|zk+l|>0 to a rational function in z1,···,zk+l,z with the only possible poles zi=0 for i=1,···,k+l,z=0,zi=zjfor 1 ≤ i This series is required to be absolutely convergent in the region|zm+1|>|z1− zm+1|> ···>|zm− zm+1|>0 to a rational function in z1,···,zm+1of the form above.There are certainly many different ways to compose Ψ with m vertex operators.They are all required to be absolutely convergent in suitable regions to rational functions in z1,···,zm+1of the form above. To calculate explicitly the cohomology of a grading-restricted vertex algebra,we need to find all the cochains first.Thus the first problem in such a calculation is to determine all the maps from the n-th tensor power of V to the space of-valued rational functions in variables z1,···,znsatisfying the convergence condition.This is in general not an easy problem,even for a relatively simple vertex algebra.For example,if we want to calculate the second cohomology of a grading-restricted vertex algebra V,we need to determine all those maps of the form(8.1)such that the convergence condition holds.For example,in the case m=1 above,we need to determine in particular whether are absolutely convergent in the region|z1|>|z2|>0 to a rational function in z1and z2with the only possible poles at z1=0,z2=0 and z1− z2=0.Note that Ψ(v1,z1)and YV(v2,z2)or YW(v1,z1)and Ψ(v2,z2)do not have to satisfy the weak commutativity,as we have discussed in Section 2,the method in Section 2 cannot be used to determine such Ψ.So we have the following problem. Problem 8.1 Is there a general method that can be used to determine all the cochains?Are there algebraic conditions on V and W such that we can determine all the cochains coposable with m vertex operators using these algebraic conditions? Another convergence problem related to the cohomology theory appeared in the work[29]of Qi and the author.It has been proved in[19]that the first cohomology of a grading-restricted vertex algebra V with coefficients in a grading-restricted generalized V-module W is isomorphic to the space of derivations from V to W modulo the space of inner derivations.In[29],it is proved that if every derivation from V to W is the sum of an inner derivation and a derivation called zero-mode derivation for every Z-graded bimodules when V is viewed as a meromorphic open-string vertex algebra,then every lower-bounded generalized V-module satisfying a composability condition is completely reducible.In this result,the complete reducibility holds only for lower-bounded generalized V-module satisfying a composability condition.This composability condition is in fact a convergence condition. We now describe this composability condition.Let W be a lower-bounded generalized V-module and W2be a V-submodule of W.We say that the pair(W,W2)satisfies the composability condition if there exists a graded subspace W1of W such that W=W1⊕W2as a graded vector space and for v,v1,···,vk+l∈V,w′2∈W′2and w1∈W1is absolutely convergent in the region|z1|>···|zk|>|z|>|zk+1|> ···>|zk+l|>0 to a rational function in z1,···,zk+l,z with the only possible poles zi=0 for i=1,···,k+l,z=0,zi=zjfor 1 ≤ i Assume that V contains a subalgebra V0such that the following conditions for intertwining operators among grading-restricted generalized V0-modules are satisfied: (1)For any n∈Z+,products of n intertwining operators among grading-restricted generalized V0modules evaluated at z1,···,znare absolutely convergent in the region|z1|>···>|zn|>0 and can be analytically extended to(possibly multivalued)analytic functions in z1,···,znwith the only possible singularities(branch points or poles)zi=0 for i=1,···,n and zi=zjfor i,j=1,···,n,i/=j. (2)The associativity of intertwining operators among grading-restricted generalized V0-modules holds. Then it is proved in[29]that for a lower-bounded generalized V-module W,a lower-bounded generalized V-submodule W2of W and a lower-bounded generalized V0-submodule W1of W such that W=W1⊕W2,the pair(W,W2)satisfies the composability condition.In particular,W satisfies the composability condition. This result on the composability requires that there is a nice subalgebra V0of V.This is in general not true. In[36],Qi studied the composability condition in the case that V is a Virasoro vertex operator algebra.For certain special V-modules and their submodules,he proved the composability conditions. We have the following main convergence problem related to this complete reducibility theorem in[29]. Problem 8.2 Are there algebraic conditions on V,W and W2such that the pair(W,W2)satisfies the composability condition if these algebraic conditions are satisfied? Acknowledgements The author gave an online minicourse“Convergence in conformal field theory”based on the material in this paper in the School on Representation theory,Vertex and Chiral Algebras,IMPA,Rio de Janeiro,March 14—18,2022.The author would like to thank the organizers,especially,Jethro van Ekeren for the invitation and arrangement.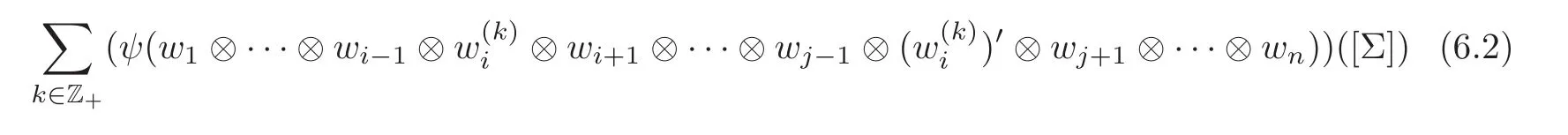
7 Convergence Conjectures and Problems in Orbifold Conformal Field Theory
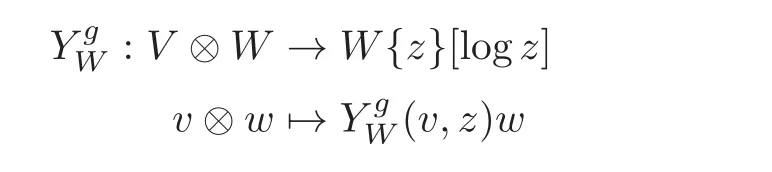



8 Convergence Problems in the Cohomology Theory of Vertex Algebras

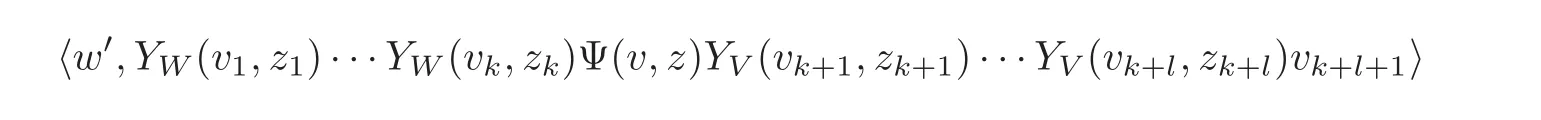
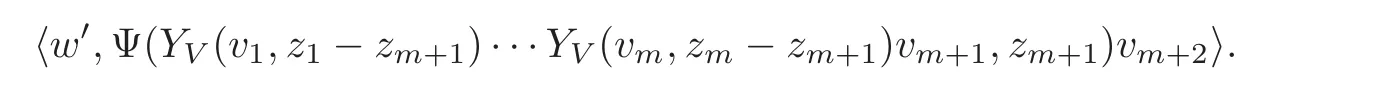
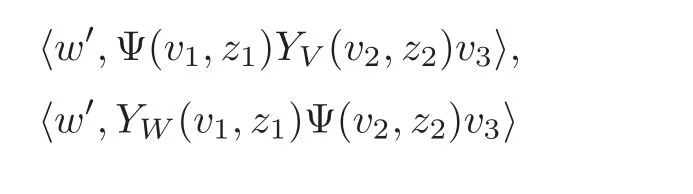
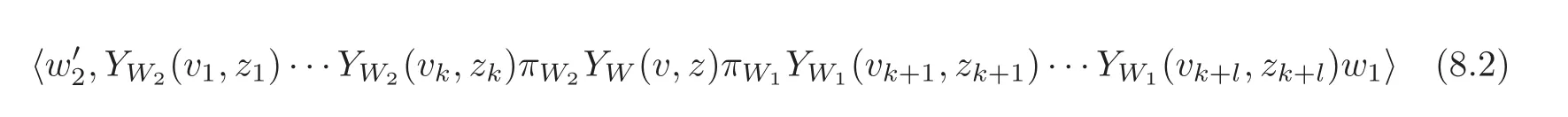
杂志排行
Chinese Annals of Mathematics,Series B的其它文章
- Long-time Asymptotic Behavior for the Derivative Schrödinger Equation with Finite Density Type Initial Data∗
- Generalized Maximum Principles and Stochastic Completeness for Pseudo-Hermitian Manifolds∗
- Local Well-posedness of the Derivative Schrödinger Equation in Higher Dimension for Any Large Data
- Turnpike Properties for Stochastic Linear-Quadratic Optimal Control Problems∗
- Holomorphic Curves into Projective Varieties Intersecting Closed Subschemes in Subgeneral Position∗
- Recent Progress in Applications of the Conditional Nonlinear Optimal Perturbation Approach to Atmosphere-Ocean Sciences∗
