Turnpike Properties for Stochastic Linear-Quadratic Optimal Control Problems∗

Jingrui SUN Hanxiao WANG Jiongmin YONG

Abstract This paper analyzes the limiting behavior of stochastic linear-quadratic optimal control problems in finite time-horizon[0,T]as T→∞.The so-called turnpike properties are established for such problems,under stabilizability condition which is weaker than the controllability,normally imposed in the similar problem for ordinary differential systems.In dealing with the turnpike problem,a crucial issue is to determine the corresponding static optimization problem.Intuitively mimicking the deterministic situations,it seems to be natural to include both the drift and the diffusion expressions of the state equation to be zero as constraints in the static optimization problem.However,this would lead us to a wrong direction.It is found that the correct static problem should contain the diffusion as a part of the objective function,which reveals a deep feature of the stochastic turnpike problem.

Keywords Turnpike property,Stochastic optimal control,Static optimization,Linear-quadratic,Stabilizability,Riccati equation

1 Introduction

Let(Ω,F,P)be a complete probability space on which a standard one-dimensional Brownian motion W={W(t)|t≥ 0}is defined.Denote by F={Ft}t≥0the usual augmentation of the natural filtration generated by W.For a random variable ξ,we write ξ∈ Ftif ξ is Ft-measurable;and for a stochastic process X,we write X∈F if it is progressively measurable with respect to the filtration F.

Consider the following controlled linear stochastic differential equation(SDE for short)

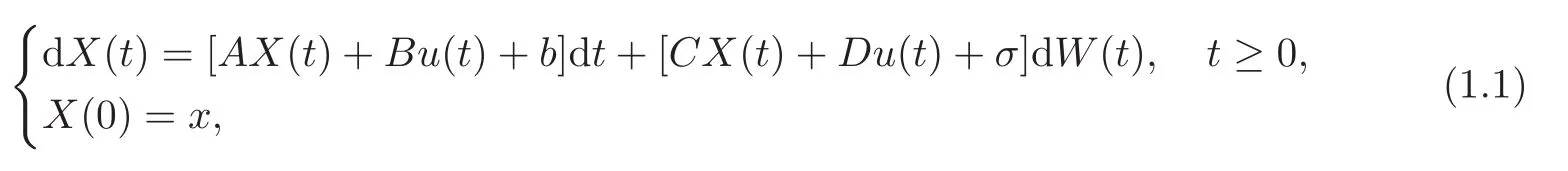
and the following general quadratic cost functional

Namely,in a big portion[δT,(1 − δ)T]of time interval[0,T],the optimal pair(XT(·),uT(·))is exponentially close to the point(x∗,u∗).This will give us an essential picture of the optimal pair without solving the problem analytically,which is very useful in applications.

The study of turnpike phenomena for deterministic problems can be traced back to the work of von Neumann[15]on problems in economics.In 1958,Dorfman,Samuelson and Solow[5]coined the name “turnpike” which was used in the highway system of the United States.Since then the turnpike phenomena have attracted considerable attentions,not only in mathematical economy(see[14]),but also in many other fields such as mathematical biology(see[9])and chemical processes(see[19]).It is well-known by now that the turnpike property is a general phenomenon which holds for a large class of variational and optimal control problems.Numerous relevant results have been established for finite and infinite dimensional problems in the context of deterministic discrete-time and continuous-time systems(see,e.g.,[2—3,7,13,23—24,27—30]and the references cited therein).In particular,we mention the papers[4,6]for discrete-time LQ problems and the papers[17—18]for continuous-time LQ problems of ordinary differential equations.

The study of turnpike phenomena for stochastic optimal control problems is quite lacking in literature.In this paper,we shall carry out a thorough investigation on the turnpike property for the stochastic LQ optimal control problem introduced earlier.Note that when C=0,D=0 and σ=0,Problem(SLQ)Treduces to a deterministic LQ problem,for which the exponential turnpike property has been established in[17]and[24]under controllability and observability assumptions.For the deterministic LQ problem(i.e.,the case of C=0,D=0,σ=0),the associated static optimization problem,which is used to determine the point(x∗,u∗),reads

To establish the turnpike property for the stochastic LQ problem,suggested by the deterministic situation,one might naively introduce the following static optimization problem:

Assume the above admits an optimal solution(x∗,u∗).Then one tries to show that the optimal pairof Problem(SLQ)Tsatisfies(1.5).However,by a little careful observation of the above,one immediately realizes that(1.8)seems to be not natural because the condition that ensuring such an optimization problem to be feasible is already very restrictive:The two equality constraints might be contradicting each other.It turns out that(1.8)is not the correct one,which will be shown later in this paper.As a main contribution of this paper,we find that the correct formulation of the static optimization problem is as follows:

one will have a unique positive definite solution P to the above ARE(1.10),and problem(1.9)is not only feasible,but also admits a unique solution(x∗,u∗).We will show that there exist positive constants K,µ>0,independent of T,such that(1.5)holds,and the adjoint process(·)will also have the same turnpike property.Note that by a(classical)standard condition,we mean that Q−STR−1S is merely positive semidefinite,which could even be 0.In such cases,P might not be positive definite,and(x,u) → F(x,u)might not be coercive.Therefore,it is unclear if the optimal solution(x∗,u∗)exists,or it might not be unique.This might bring some additional issues into the study and we will try to address that in our future publications.Also,we note that for the state equation,stabilizability is strictly weaker than the(null)controllability which was assumed in[13,17,24]for deterministic problems.For the study of controllability of linear SDEs,see[25].

The rest of the paper is organized as follows.In Section 2,we give the preliminaries and collect some relevant results on stochastic LQ optimal control problems.In Section 3 we recall the notion of stabilizability and formulate the correct static optimization problem.The convergence of the solution to a related differential Riccati equation as the time-horizon tends to infinity will be presented in Section 4.In Section 5,we study the static optimization problem associated to Problem(SLQ)Tand establish the turnpike property of Problem(SLQ)Tas well as of the adjoint process.Some concluding remarks are collected in Section 6.

2 Preliminaries

We begin with some notation that will be frequently used in the sequel.Let Rn×mbe the space of(n×m)real matrices equipped with the Frobenius inner product

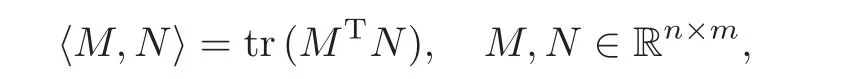
where MTdenotes the transpose of M and tr(MTN)is the trace of MTN.The norm induced by the Frobenius inner product is denoted by|·|.For a subset H of Rn×m,we denote by C([0,T];H)the space of continuous functions from[0,T]map into H,and by L∞(0,T;H)the space of Lebesgue measurable,essentially bounded functions from[0,T]map into H.Let Snbe the subspace of Rn×nconsisting of symmetric matrices andthe subset of Snconsisting of positive definite matrices.For Sn-valued functions M(·)and N(·),we write M(·) ≥ N(·)(respectively,M(·)>N(·))if M(·)−N(·)is positive semidefinite(respectively,positive definite)almost everywhere with respect to the Lebesgue measure.The identity matrix of size n is denoted by In,and a vector always refers to a column vector if not specified.Also,recall that W={W(t)|t ≥ 0}is a standard one-dimensional Brownian motion,F={Ft}t≥0is the usual augmentation of the natural filtration generated by W,and that U[0,T]is the space of Rm-valued,F-progressively measurable,square-integrable processes over[0,T].

For the purpose of later presentation,we recall some results of time-variant stochastic LQ problem in finite time-horizon.Consider the state equation

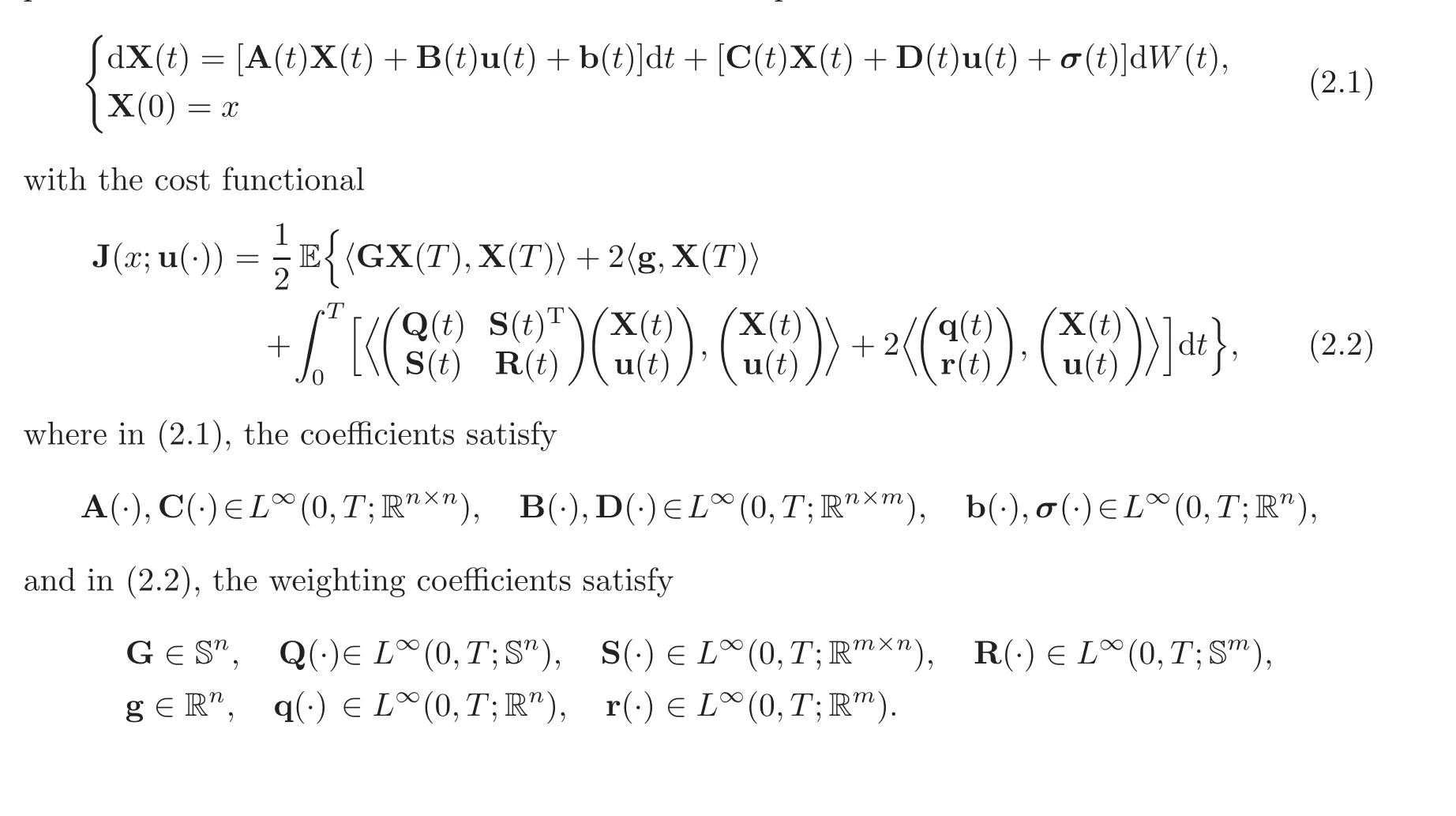
In the case that b=σ=q=0,we denote the corresponding optimal control problem by Problemand call it a homogenous LQ problem on[0,T].The value function of Problemis denoted by

3 Stabilizability and the Static Optimization Problem

Consequently,Problem(O)is well-formulated and admits a unique optimal solution.

From the above examples,together with our main result on the turnpike property of Problem(SLQ)Twhich will be presented a little later,we see that(1.8)is not a suitable problem to be considered and the correct one is Problem(O).

4 Convergence of the Riccati Equation

According to Lemma 2.1,we know that under(H1)—(H2),for each T>0,Problem(SLQ)Tadmits a unique optimal control for every initial state x.Moreover,the following conclusions hold:

5 The Turnpike Property

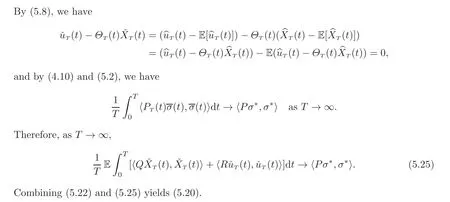
We point out that for general situation,namely,the state equation(1.1)and the cost functional(1.2),we may carry out the procedure(with more complicated notation)to get the same results,or transform back from the results for the reduced problem.The general conditions ensuring the results are the stabilizability of the system[A,C;B,D]and the stronger standard condition(1.11)for the weighting functions of the cost functional.

6 Concluding Remarks

For linear-quadratic stochastic optimal control problems in finite time-horizon,we have established the turnpike property under the natural condition of stabilizability of the controlled linear SDE and the strong standard condition of the quadratic cost functional.The crucial contribution of the current paper is to find the correct form of the corresponding static optimization problem in which the diffusion part of the state equation should be getting into the cost functional,rather than taking it to be as an additional equality constraint.Such an idea should have big impact on the study of turnpike type problems for general stochastic optimal control problems.We will report some further results along this line in our future publications.

Acknowledgements The authors would like to thank the associate editor and the anonymous referees for their suggestive comments,which lead to this improved version of the paper.