Local Well-posedness of the Derivative Schrödinger Equation in Higher Dimension for Any Large Data

Boling GUO Zhaohui HUO

Abstract In this paper,the authors consider the local well-posedness for the derivative Schrödinger equation in higher dimension

Keywords Well-posedness,Derivative Schrödinger equation in higher dimension,Short-time Xs,b,Large initial data

1 Introduction

The aim in this work is to study the well-posedness for the Cauchy problem of the Schrödinger equation with derivative in higher dimension(DNLS):

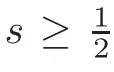
From above known results,it follows that there exists an open problem:How about solution of(1.1)in high dimension with large data?For large data,Kenig,Ponce and Vega[10]obtained local well posedness of the generalized DNLS equation(1.2)in Hswith s≫.Moreover,Bienaim´e[1]considered the generalized DNLS equation(1.2),and proved the local existence,the uniqueness and the smoothing effect given any u0∈ Hswith s>+3;his proof followed the same plan as that of Kenig,Ponce and Vega[10].In this paper,we will consider the solution of(1.1)for large data,DNLS equation(1.1)is simpler than DNLS equation(1.2).In fact,we can also use the stand energy method in[4]to show that the Cauchy problem(1.1)is locally well-posed in Hswith s>+1 for any large initial data.From the result in one dimension,there exists a gap betweenandin high dimension.In this paper,we will solve this gap except for the endpoint space Hn2.That is,the Cauchy problem(1.1)is locally well-posed in Hswith s>for any large initial data.Moreover,from the following proof,it follows that the flow map defines a continuous map on Hswith s>,not a uniformly continuous map.But basing on the method in this paper,we will show that the Cauchy problem(1.2)is locally well-posed in Hswith s>+1 for any large initial data in the future.

2 Definitions and Notations

3 Multilinear Estimates

4 Linear Estimates,Trilinear Estimates,Energy Estimates,Well-posedness of DNLS Equation

In this section,we give the proof of Theorem 1.1.In Theorem 1.1,we show that the Cauchy problem(1.1)is locally well-posed in space Hsfor any large initial data.

Lemma 4.1 If Fuk∈Xkwith k≥1,then

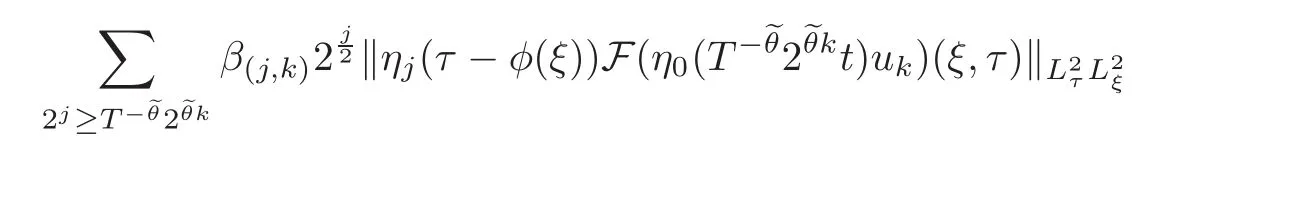
5 Dyadic Trilinear Estimates

6 Trilinear Estimates

7 Energy Estimates