Holomorphic Curves into Projective Varieties Intersecting Closed Subschemes in Subgeneral Position∗
2022-12-06QingchunJIJunYAOGuangshengYU
Qingchun JI Jun YAO Guangsheng YU
Abstract In this paper,the authors introduce the index of subgeneral position for closed subschemes and obtain a second main theorems based on this notion.They also give the corresponding Schmidt’s subspace type theorem via the analogue between Nevanlinna theory and Diophantine approximation.
Keywords Nevanlinna theory,Second main theorem,Holomorphic curve,Subgeneral position,Closed subschemes,Schmidt’s subspace theorem
1 Introduction
In higher dimensional Nevanlinna theory,the second main theorem of holomorphic curves into complex varieties intersecting subvarieties is a main research content.Recently,there are many developments in extending the second main theorem for divisors to arbitrary closed subschemes.To state some of the results,we recall the following notions.

Thus the divisors are in general position if they are in(dim X)-subgeneral position.


Remark 1.1 If Y1,···,Yqare of locally complete intersection closed subschemes intersecting properly on X,then they are in general position.The converse holds if X is Cohen-Macaulay(this is true if X is nonsingular)by[3,Theorem 17.4].Thus,if X is a smooth projective variety,then the subschemes Y1,···,Yq,which are of locally complete intersection,are in m-subgeneral position with index κ,if and only if,the subschemes Y1,···,Yqare in m-subgeneral position and for any set J ⊂ {1,···,q}with|J|≤ κ,Yj,j ∈ J intersect properly.
The purpose of this paper is to extend Theorem 1.2 to the case of closed subschemes.Here is our main result.
Theorem 1.4(Main Theorem)Let X be a smooth complex projective variety,and let Y1,···,Yqbe closed subschemes,which are of locally complete intersection,in m-subgeneral position with index κ on X.Let L be a big line sheaf on X.Let f:C → X be an algebraically non-degenerate holomorphic curve.Then,for every ε>0,
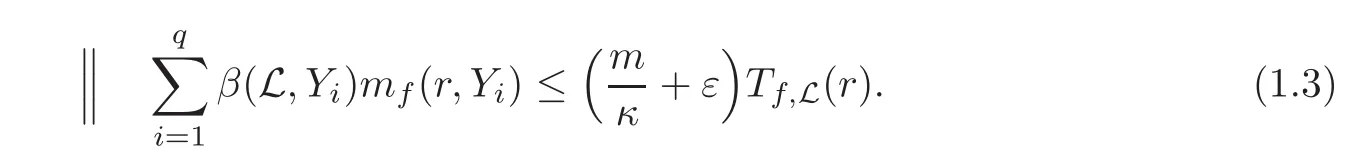
Remark 1.2 We assume that X is smooth and the closed subschemes Y1,···,Yqare of locally complete intersection in Theorem 1.4,because we use the filtration which is valid for properly intersecting closed subschemes.If the closed subschemes Y1,···,Yqare in m-subgeneral position and for any set J ⊂ {1,···,q}with|J|≤ κ,Yj,j ∈ J intersect properly,then we do not need these assumptions.When the closed subschemes intersect proplerly,we can take m= κ =dim X,thus our main theorem recovers Ru-Wang’s result in[6].
2 Preliminaries on Nevanlinna Theory
In this section,we briefly recall some definitions and facts in Nevanlinna theory.
2.1 Weil functions
We briefly recall the basic definition of Weil functions,one can refer to[7]for more details.Let Y be a closed subscheme of a projective variety X.One can associate a Weil function λY:XSupp Y →R,well-defined up to O(1),which satisfies the following properties:If Y and Z are two closed subschemes of X,and φ :X′→ X is a morphism of projective varieties,
(i)λY∩Z=min{λY,λZ};
(ii)λY+Z= λY+λZ;
(iii)λY≤ λZ,if Y ⊂Z;
(iv) λY(φ(x))= λφ∗Y(x).
In particular,let D be a Cartier divisor on a complex projective variety X.A Weil function with respect to D is a function λD:(XSupp D)→ R such that for all x ∈ X there is an open neighborhood U of x in X,a nonzero rational function f on X with D|U=(f),and a continuous function α:U →R such that
8.One of the most beautiful girls: Hyperbole is frequently used to describe beauty in fairy tales. Each beautiful woman has no equal or is the most beautiful or similar. Beauty often represents goodness, worthiness28, privilege, and wealth in fairy tales. Princesses are especially expected to be beautiful. Physical beauty is often considered to represent inner beauty in folklore, except for when it is a magical disguise. Return to place in story.

for all x∈(USupp D).Note that a continuous fiber metric‖·‖on the line sheaf OX(D)determines a Weil function for D given by λD(x)= −log ‖s(x)‖ where s is the rational section of OX(D)such that D=(s).
The Weil functions with respect to divisors satisfy the following properties:
(a)Functoriality:If λ is a Weil function for a Cartier divisor D on X,and if φ :X′→ X is a morphism such that φ(X′)/⊂ Supp D,then x → λ(φ(x))is a Weil function for the Cartier divisor φ∗D on X′.
(b)Additivity:If λ1and λ2are Weil functions for Cartier divisors D1and D2on X,respectively,then λ1+ λ2is a Weil function for D1+D2.
(c)Uniqueness:If both λ1and λ2are Weil functions for a Cartier divisor on X,then λ1= λ2+O(1).
(d)Boundedness from below:If D is an effective divisor and λ is a Weil function for D,then λ is bounded from below.
Lemma 2.1(see[7,Lemma 2.2])There exist effective Cartier divisors D1,···,Dℓsuch that
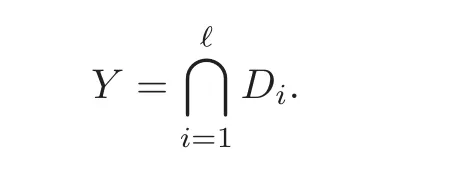
By Lemma 2.1,we can assume that Y=D1∩ ···∩ Dℓ,where D1,···,Dℓare effective Cartier divisors.This means that IY=ID1+ ···+IDℓ,where IY,ID1,···,IDℓare the defining ideal sheaves in OX.We set
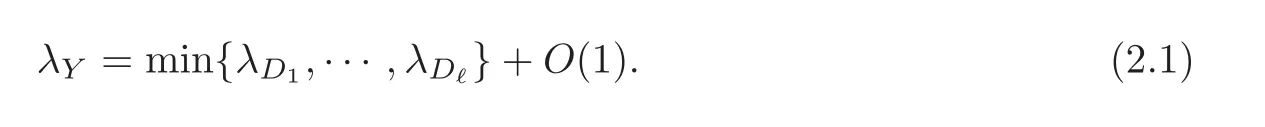
Then we have λY:XSupp Y → R,which does not depend on the choice of Cartier divisors.
2.2 Characteristic function
Let X be a complex projective variety and f:C→X be a holomorphic map.Let L→X be an ample line sheaf and ω be its Chern form.We define the characteristic function of f with respect to L by
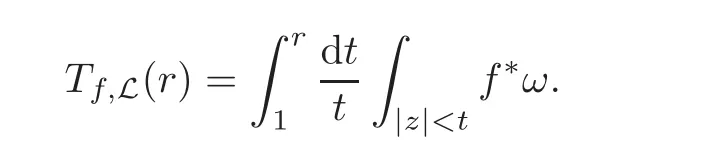
Since any line sheaf L can be written aswith L1,L2being both ample,we define Tf,L(r)=Tf,L1(r)−Tf,L2(r).A divisor D on X defines a line bundle O(D),we denote by Tf,D(r)=Tf,O(D)(r).If X=Pn(C)and L=OPn(C)(1),then we simply write Tf,OPn(C)(1)(r)as Tf(r).
The characteristic function satisfies the following properties:
(a)Functoriality:If φ :X → X′is a morphism and if L is a line sheaf on X′,then
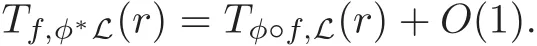
(b)Additivity:If L1and L2are line sheaves on X,then
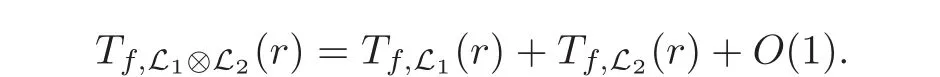
(c)Positivity.If L is ample and f:C→X is non-constant,then
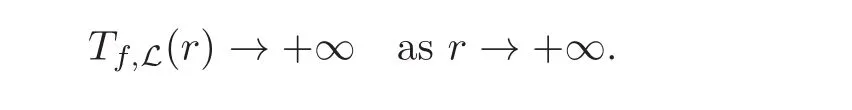
(d)Base locus:If the image of f is not contained in the base locus of|D|,then Tf,D(r)is bounded from below.
(e)Globally generated line sheaves:If L is a line sheaf on X,and is generated by its global sections,then Tf,L(r)is bounded from blow.
2.3 Proximity functions
Let X be a projective variety and let Y⊂X be a closed subscheme.For a holomorphic curve f:C → X with f(C)/⊂ Supp Y,the proximity function of f with respect to Y is defined by
2.4 A general form of Cartan’s second main theorem
To prove our main theorem,we need the following general form of Cartan’s second main theorem given by Ru and Vojta[4].
Theorem 2.1(see[4,Theorem 2.8]Let X be a complex projective variety,and let L be a line sheaf on X.Let V be a linear subspace of H0(X,L)with dim V>1,and let s1,···,sqbe nonzero elements of V.For each j=1,···,q,let Djbe the Cartier divisor(sj).Let f:C → X be an algebraically non-degenerate holomorphic curve.Then,for every ε>0,
3 Proof of Main Theorem
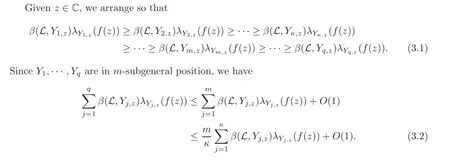



4 Schmidt’s Subspace Theorems
In this section,we introduce the counterpart in number theory of our main theorem according to Vojta’s dictionary which gives an analogue between Nevanlinna theory and Diophantine approximation(see[8—9]).
Let k be a number field.Denote by Mkthe set of places(i.e.,equivalence classes of absolute values)of k and writefor the set of archimedean places of k.
Let X be a projective variety defined over k,let L be a line sheaf on X and let Y be a closed subscheme.For every place v∈Mk,we can associate the Weil functions(or local heights)λL,vand λY,vwith respect to v,which have similar properties as the Weil function introduced in Section 2(see[7]).Define
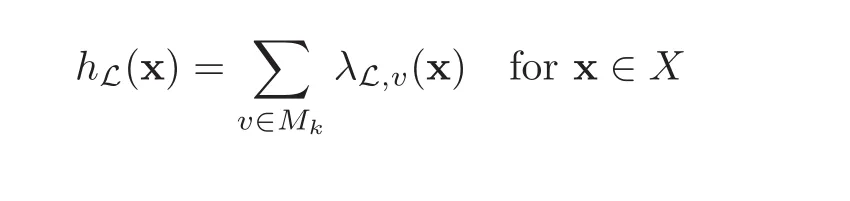

杂志排行
Chinese Annals of Mathematics,Series B的其它文章
- On the Generalized Geroch Conjecture for Complete Spin Manifolds∗
- Holomorphic Retractions of Bounded Symmetric Domains onto Totally Geodesic Complex Submanifolds
- Convergence in Conformal Field Theory
- Heat Transfer Problem for the Boltzmann Equation in a Channel with Diffusive Boundary Condition∗
- Extrapolated Smoothing Descent Algorithm for Constrained Nonconvex and Nonsmooth Composite Problems∗
- Recent Progress in Applications of the Conditional Nonlinear Optimal Perturbation Approach to Atmosphere-Ocean Sciences∗
