Extrapolated Smoothing Descent Algorithm for Constrained Nonconvex and Nonsmooth Composite Problems∗

Yunmei CHENHongcheng LIU Weina WANG

Abstract In this paper,the authors propose a novel smoothing descent type algorithm with extrapolation for solving a class of constrained nonsmooth and nonconvex problems,where the nonconvex term is possibly nonsmooth.Their algorithm adopts the proximal gradient algorithm with extrapolation and a safe-guarding policy to minimize the smoothed objective function for better practical and theoretical performance.Moreover,the algorithm uses a easily checking rule to update the smoothing parameter to ensure that any accumulation point of the generated sequence is an(affine-scaled)Clarke stationary point of the original nonsmooth and nonconvex problem.Their experimental results indicate the effectiveness of the proposed algorithm.

Keywords Constrained nonconvex and nonsmooth optimization,Smooth approximation,Proximal gradient algorithm with extrapolation,Gradient descent algorithm,Image reconstruction

1 Introduction

Nonconvex and nonsmooth composite problems have been receiving much attention in modern science and technology,such as signal processing(see[9,17,51]),image restoration(see[19,32,34,49])and image reconstruction(see[2,15,33,39—40]).This is mainly because of their superior ability to produce sparser solutions and recover images with neater edges(see[11,22,32—34,49]).In particular,compared to unconstrained nonconvex models,the corresponding constrained models can achieve reasonable improvements when most pixel intensities of an image are around the boundary of a closed convex set(see[3—6,10,12,24,41,51]).In this paper,we focus on the following constrained nonconvex nonsmooth composite minimization

where Ω is a closed convex set,r(u)is a nonconvex possibly non-Lipschitz function and h(u)is a smooth function and possibly nonconvex.In image processing problems,r(u)in(1.1)can be considered as the regularization term dependent on the prior knowledge of images,such asℓpregularization(0 ≤ p<1)(see[2,12,19,22,45,48—49,51]),h(u)can be considered as the fidelity term for measuring the deviation of a solution from the observation,such as the least squares data fitting term(see[2,37,43])and Ω is usually a box constrained set.

Algorithms for solving the nonsmooth and nonconvex problems of form(1.1)have been studied extensively,due to their wide range of applications.If h is smooth(possibly nonconvex)and r is simple(i.e.,its proximal operator has a closed form solution or the proximal point is easy to compute),the proximal gradient method(also known as the forward-backward splitting)is very effective(see[1,7,18,29]).An abstract convergence result for nonconvex descent methods including proximal gradient and gradient descent algorithms under a sufficient decrease condition and a relative inexact optimality condition has been presented in[1].For non-simple r,several inexact proximal gradient and gradient descent algorithms have developed to reduce computational cost while still ensuring convergence under certain conditions(see[1,21,24—25,28,30,38,47]).Moreover,a number of works were proposed to integrate the Nesterov’s accelerated gradient descent algorithm into the proximal gradient algorithm for improved iteration efficiency while maintaining convergence guarantee for nonconvex programming(see[20,27—28,39,42]).The iPiano algorithm combined proximal gradient method with an inertial force has better performance and nice convergence properties(see[35,44]).However,most of standard or accelerated and/or inexact proximal gradient algorithms for nonconvex programming require r to be smooth or satisfy the Kurdyka-Lojasiewicz(KL for short)inequality for global convergence(see[1,27,44,46]).In this work we consider more general nonconvex nonsmooth problem composed of gradient operators,which may not satisfy these conditions.

For more general nonconvex and nonsmooth optimization problems,especially for the nonconvex component being also nonsmooth,a natural choice is to use the smoothing strategy(see[4—6,11—14,22,26,33—34,36]).Smoothing methods construct a sequence of smooth nonconvex problems to approximate the original nonsmooth problem,and each smooth problem with the fixed smoothing parameter can be solved by efficient algorithms such as the gradient descent method combined with line search(see[11]),the nonlinear conjugate gradient method(see[14])and the trust region Newton method(see[13]).By updating the smoothing parameter,smoothing algorithms are able to solve the original nonsmooth nonconvex optimizations and any accumulation point of the generated sequence is a Clarke stationary point when the gradient consistency of subdifferential associated with a smoothing function is proved(see[4—6,11—14]).For instance,[4]discussed the first order necessary optimality condition for local minimizers and defined the generalized stationary point for a class of constrained nonsmooth nonconvex problems where the feasible set is a closed convex set.Recently,to accelerate the smoothing method for nonconvex problems,[39]introduced a convergent smoothing gradient descent type algorithm with extrapolation technique.It can not only guarantee that any accumulation point is an(affine-scaled)Clarke stationary point,but also obtain better experimental results compared to the standard smoothing gradient descent method.Instead of directly converting the nonsmooth function into parameterized smooth function,iterative support shrinking with proximal linearization algorithms(see[19,30,40—41,48])obtained a nonconvex smooth objective function by putting nondifferentiable points of the nonsmooth function into constraints.These methods were easy to produce piecewise constant regions and thus were not suitable for recovering smooth parts of images.

In this paper,we propose an accelerated smoothing descent algorithm for solving a general class of constrained nonsmooth nonconvex optimization problems,where the nonconvex term is a potential function composed with the L2norm of the gradient of the unknown function.Our algorithm adopts the proximal gradient algorithm with extrapolation and a safe-guarding policy to minimize the smoothed objective function to guarantee a better practical and theoretical performance.The smoothing method is inspired by[11],which is equivalent to Nesterov’s smoothing technique for non-smooth optimization(see[31]).Moreover,the algorithm uses a rule that is easy to implement to adoptively reduce the smoothing parameter.We can prove that any accumulation point of the generated sequence is an(affine-scaled)Clarke stationary point of the nonsmooth nonconvex problem(1.1).The main contributions are summarized as follows:

•We propose an extrapolated smoothing descent algorithm for constrained nonconvex nonsmooth minimization problems,where the nonconvex part is also nonsmooth and may not be simple or satisfy KL property.Our algorithm adopts the proximal gradient algorithm with extrapolation and a safe-guarding policy to minimize the smoothed objective function.The algorithm can also adaptively reduce the smoothing level to approach a stationary point of the original problem.

•We prove that the sequence generated by the proposed algorithm has at least an accumulation point,and any accumulation point of the sequence is an(affine-scaled)Clarke stationary point of the nonconvex and nonsmooth problem.Moreover,the total number of iterations required to terminate our algorithm with a given tolerance is also studied.

•We conduct a series of numerical experiments with comparisons to several existing descent type of algorithms with or without box constraints and with or without extrapolation for sparseview CT reconstruction.The experimental results demonstrate the effectiveness of the proposed algorithm.

The paper is organized as follows.In Section 2,we identify a class of constrained nonconvex and nonsmooth optimization problems,and present an extrapolated smoothing descent algorithm(ESDA for short)for solving the problem.In the meantime the smoothing method and properties of the smoothed objective function are studied.In Section 3,we provide convergence and iteration complexity analyses of the proposed algorithm.Experimental results are given in Section 4.At last,conclusions are summarized in Section 5.

2 The Problem and the Algorithm

2.1 Preliminaries

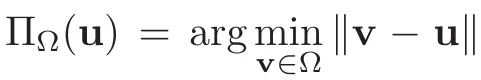
Using the definition of Clarke generalized directional derivative(see[8,16])we give the following definitions.

Definition 2.1 Assume that g:Rn→(−∞,+∞]is a locally Lipschitz continuous function.The Clarke subdifferential of g at x ∈ Rnis defined as

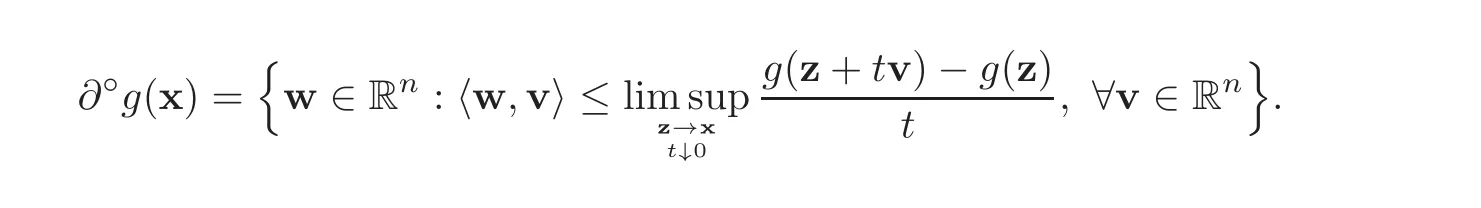
2.2 The problem and basic assumptions

2.3 The algorithm

Before we present the proposed algorithm,we first define a smooth approximation problem for the nonsmooth and nonconvex problem(2.1).

The function ϕ(‖diu‖)is nonsmooth and possibly also non-Lipschitz at ‖diu‖ =0 when ϕ′(0+)=+∞.Inspired by the approximation technique for|t|in[11],we approximate ϕ(‖diu‖)

Table 1 Nonconvex nonsmooth potential functions with a parameter β>0.

Algorithm 1:Extrapolated Smoothing Decent Algorithm(ESDA for short)for(2.1)Step 0:Input(ρ,δ,τ1)∈(0,1),τ>0,Maximum number of iterations K or tolerance εtol>0;Initialize u−1=u0 ∈ Ω,θ0=1,and η−1= η0>0.Step 1:For k=0,1,2,···,Step 1.1:Set θk+1=1+√1+4θ2 2 .Step 1.2:Let wk+1=uk+(θk−1 k)(uk−uk−1).Step 1.3:Define qk+1:θk+1(qk+1=wk+1, if Fηk(wk+1)≤ Fηk(uk)and wk+1∈ Ω,uk, otherwise. (2.10)Step 1.4:Compute buk+1:zk+1=qk+1−s0∇h(qk+1), (2.11)buk+1= ΠΩ(zk+1−sk+1∇rηk(zk+1)), (2.12)Step 1.5:Compute uk+1:uk+1= ΠΩ(uk− αk+1∇Fηk(uk)),if (2.13)Fηk(uk+1)− Fηk(uk)≤ −δ‖uk+1−uk‖2. (2.14)Otherwise,αk+1← ραk+1and go back to(2.13). (2.15)Step 1.6:Choose uk+1:(uk+1=uk+1, if Fηk( buk+1)≤ Fηk(uk+1),uk+1,otherwise. (2.16)b Step 2:Update ηk+1(ηk+1=τ1ηk, if ‖uk+1−uk‖ < τηkαk+1,ηk, otherwise.(2.17)Step 3:If τηkαk+1< εtol,terminate and output uk+1.

Note that in ESDA the generation ofin(2.11)can be viewed as using the proximal gradient algorithm with extrapolation,where s0and sk+1are stepsizes determined by user.Theplays a role in ESDA to attain better efficiency than the standard gradient descent method.Our experimental results confirmed this.However,due to the nonconvexity and nonsmoothness of problem(2.1),the sequencemay not converge.Thein(2.13)is obtained by the standard gradient descent to safeguard the convergence of the ESDA.The stepsize αk+1is determined by a simple line search strategy in(2.14).We set uk+1beingorwhichever has lower value of Fηkto encourage reduction of the objective function.

3 Convergence and Complexity Analysis

In this section,we will discuss the convergence of ESDA and the bound for the number of the iterations required to terminate the algorithm with the prescribed accuracy εtolfor

First,we give the following lemma that has been proved in[39].

Now we are ready to present the convergence result for ESDA.

Theorem 3.3 Let{uk}is the sequence generated by the ESDA with any u0∈ Ω,δ>0,εtol=0,and the maximum number of iterations K= ∞.Let{ukl+1}be the subsequence of{uk},where the reduction criterion in Step 2 is satisfied for k=kland l=1,2,···Then the following statements hold:

1.{ukl+1}has at least one accumulation point on Ω.

2.If ϕ(t)is continuously differentiable on[0,+∞),every accumulation point of{ukl+1}is a Clarke stationary point of problem(2.1).

3.If ϕ(t)is continuously differentiable only on(0,+∞),then every accumulation point of{ukl+1}is an affine-scaled Clarke stationary point of model(2.1),i.e.,if u∗is an accumulation

4 Numerical Experiments

In this section,we consider a class of box constrained problem(2.1),where Ω={u∈Rn:l1e ≤ u ≤ l2e}and e=(1,1,···,1)T∈ Rnin the application of sparse view CT reconstruction.To exam the performance of the proposed algorithm,we compare it to the standard smoothing gradient descent method to minimize the same objective function with and without box constraints,named as(BSGD for short)and(SGD for short)respectively.The BSGD is the same as the proposed algorithm without Steps 1.1—1.4.We also compare the proposed algorithm with accelerated smoothing algorithm(ESA for short)in[39]for corresponding unconstrained problem.All numerical experiments are conducted in MATLAB R2016a running on a PC with Intel Core i5 CPU at 1.6GHz and 8G of memory.Besides visual evaluation we also use peak signal-to-noise ratio(PSNR for short)to evaluate the quality of reconstruction.The PSNR is defined by

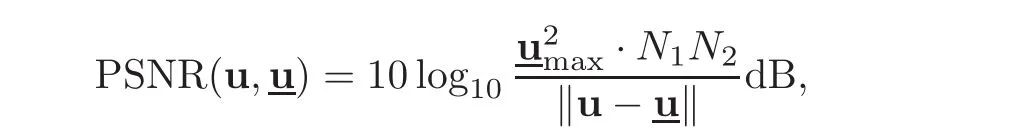
CT reconstruction problem can be modeled as an inverse problem f=Hu+υ,where u is the image to be reconstructed,H is the system matrix for CT scanner depending on the beam geometer,f is the noisy sinogram measurements and υ is the noise with normal distribution.Here,we consider 2D parallel-beam CT with an N×N domain,usingparallel rays for each angle as in[23].The regular view CT has angles 0,1,···,179,whereas the sparse view CT that we deal with has angles 0,5,10,···,175(i.e.,=36 rotated projection views).Number of parallel rays for each angle and the distance from the first ray to the last ray are set to be the nearest integer to,respectively.H is implemented by Radon transform.The images used in this experiment are the“Shepp-Logan”phantom(128× 128),“NCAT”phantom(256×256)and the cerebral phantom(512×512)(see[50])shown in Figure 1.The corresponding noisy sinograms for parallel-beam scanning with=36 are also presented in this figure.

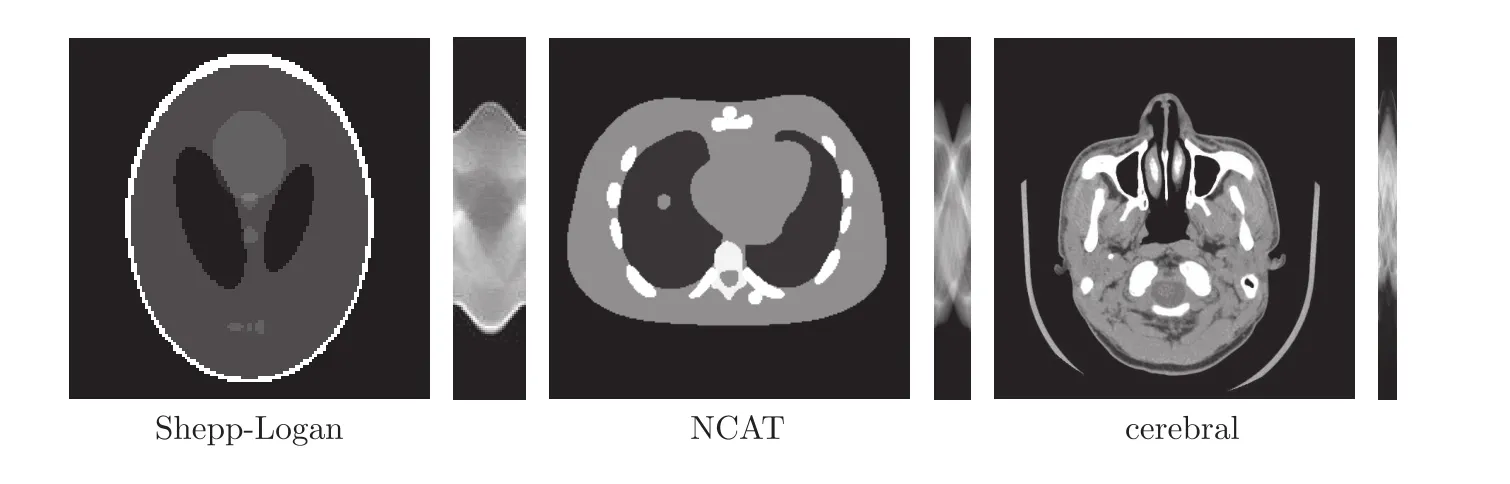
Figure 1 Test images and the corresponding sinogram observations when =36.

In Figure 4,we present reconstruction results on“cerebral”after 100 iterations with=36.In this experiment,we adopt same rules as above to tune parameters in all compared algorithms.The PSNR of reconstructed images from SGD,ESA,BSGD and proposed algorithms for three different regularization functions are shown under the image in this figure.The improvement of PSNR by the proposed algorithm is about 1.01dB,0.20dB,0.90dB increase on average for those regularization functions compared to SGD,ESA and BSGD,respectively.To better visualize the results,the zoomed regions are shown in Figure 5.

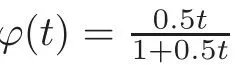
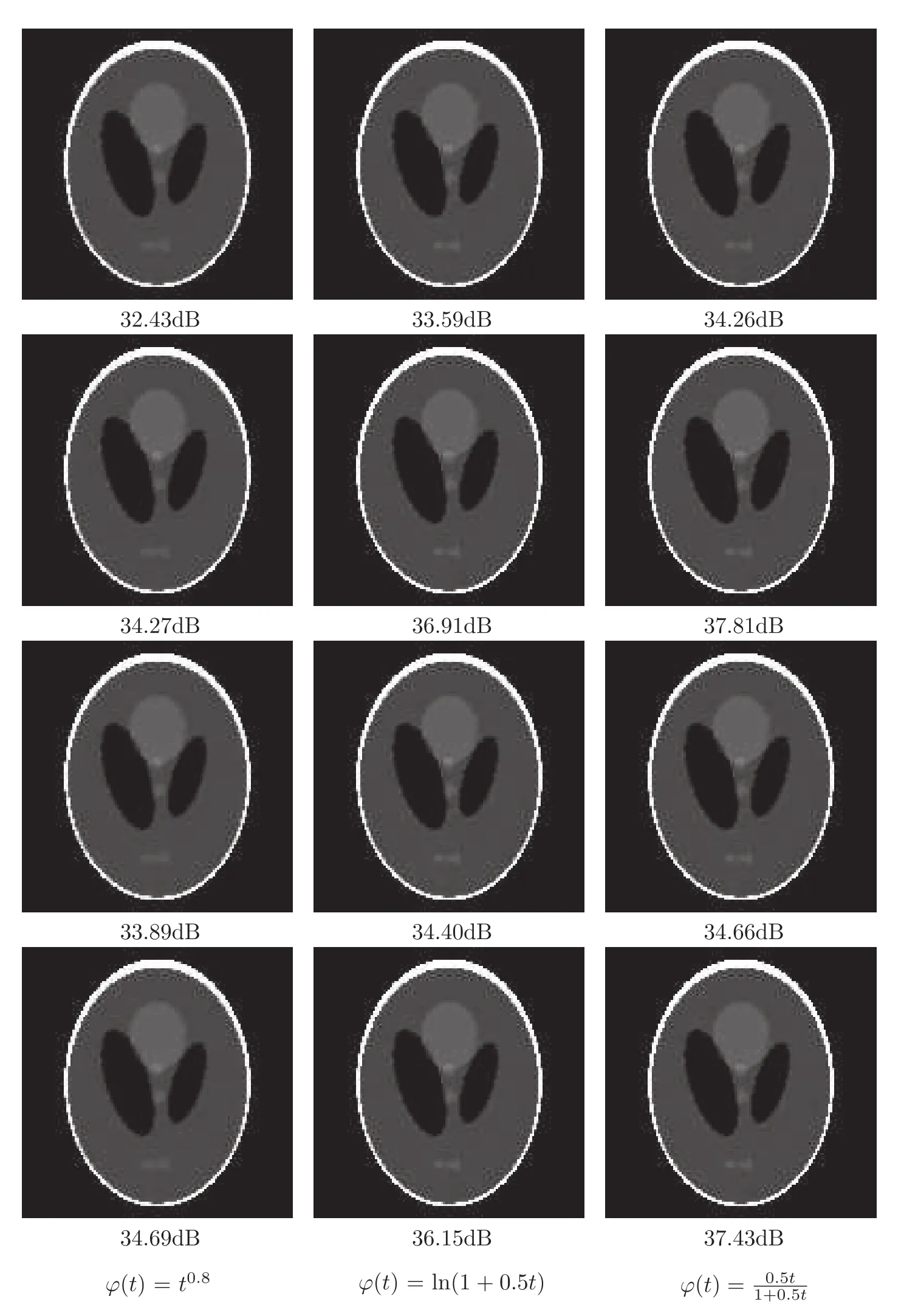
Figure 2 Results after 100 iterations on “Shepp-Logan”.From the first column to the third column:Reconstructions by different potential functions.From the first row to the fourth row:Reconstructions by SGD,ESA,BSGD and the proposed algorithm.PSNR values are listed.

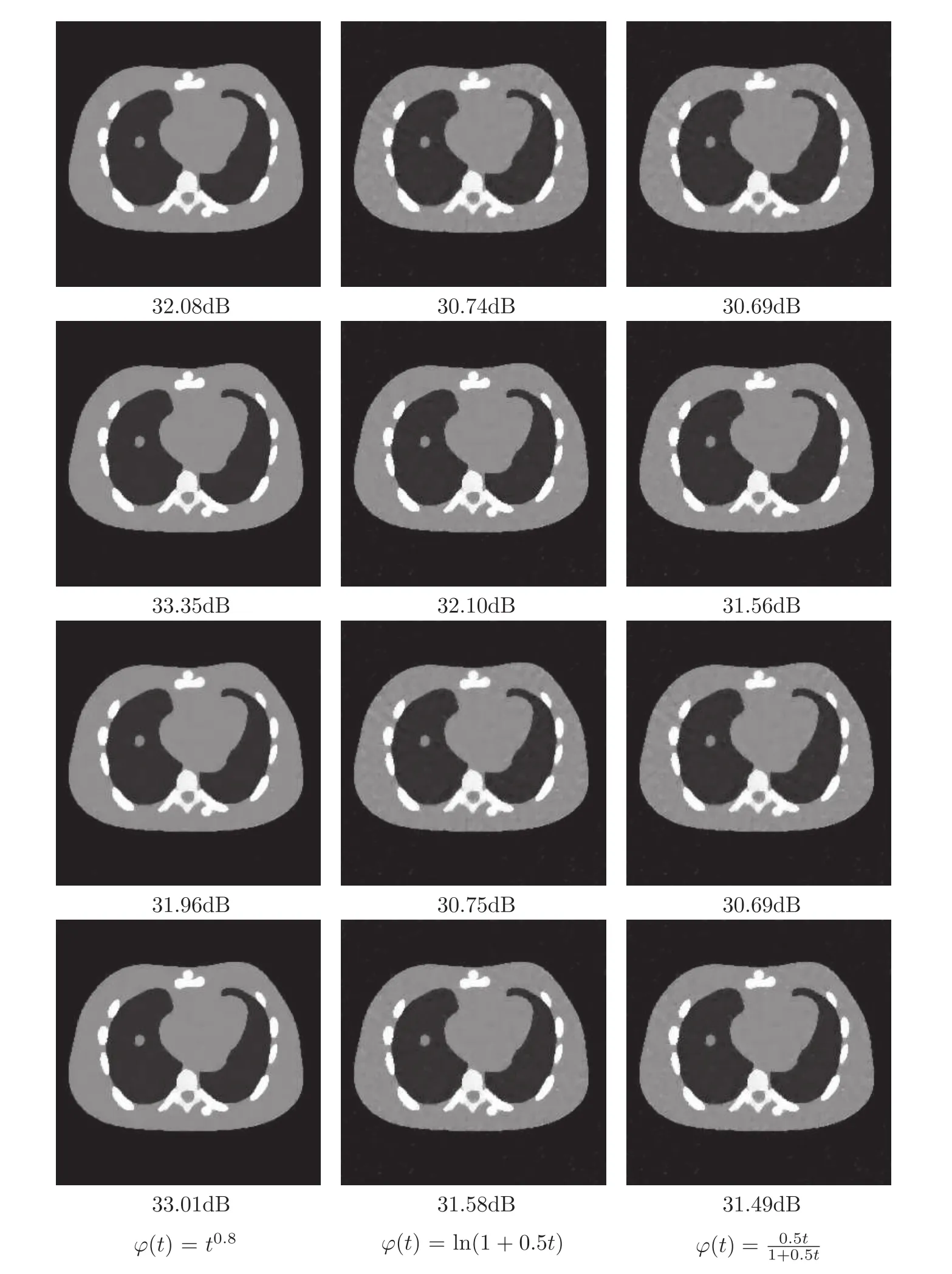
Figure 3 Results after 100 iterations on “NCAT”.From the first column to the third column:Reconstructions by different potential functions.From the first row to the fourth row:Reconstructions by SGD,ESA,BSGD and the proposed algorithm.PSNR values are listed.

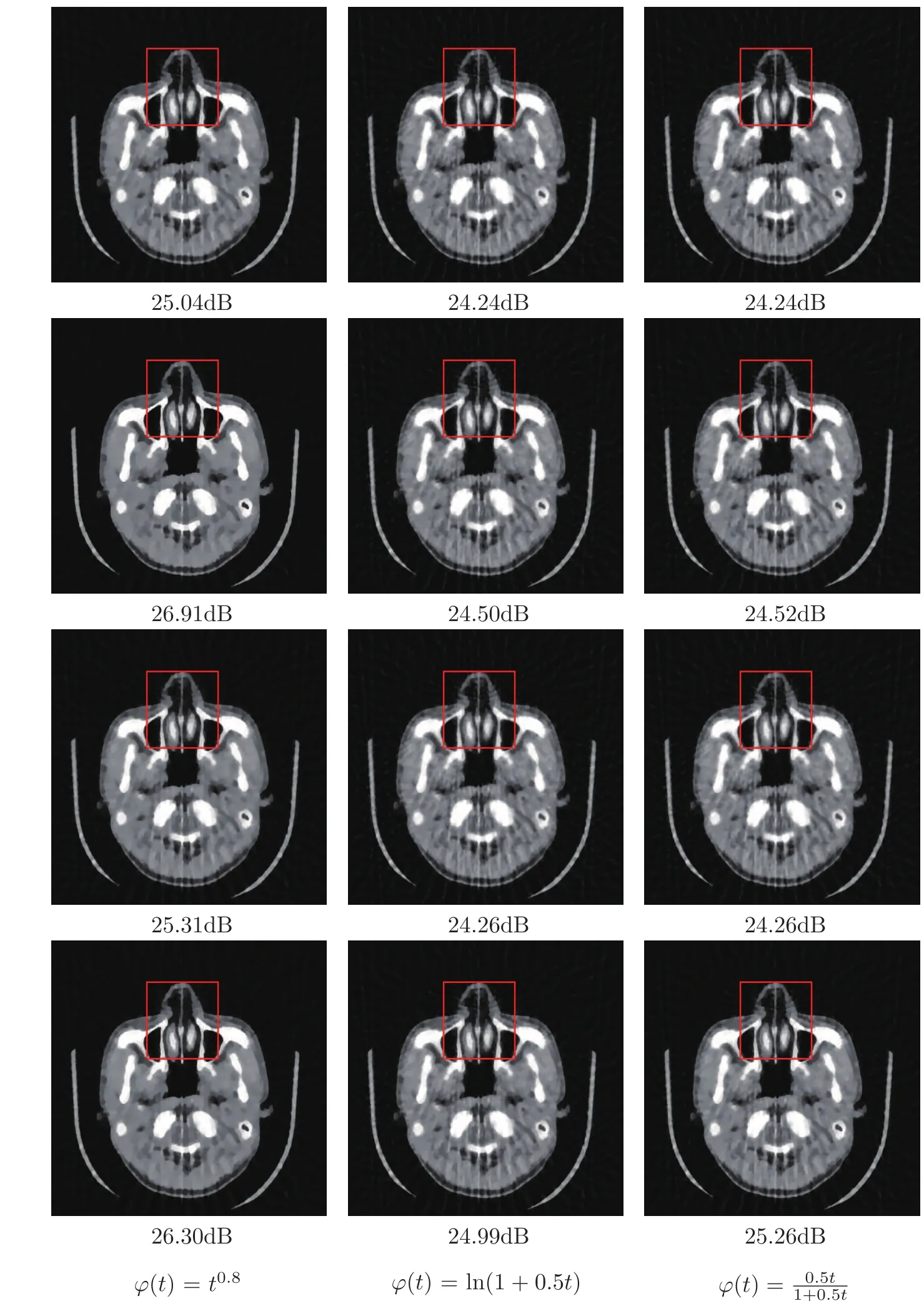
Figure 4 Results after 100 iterations on “cerebral”.From the first column to the third column:Reconstructions by different potential functions.From the first row to the fourth row:Reconstructions by SGD,ESA,BSGD and the proposed algorithm.PSNR values are listed.

Figure 5 The zoomed regions corresponding to results in Figure 4.

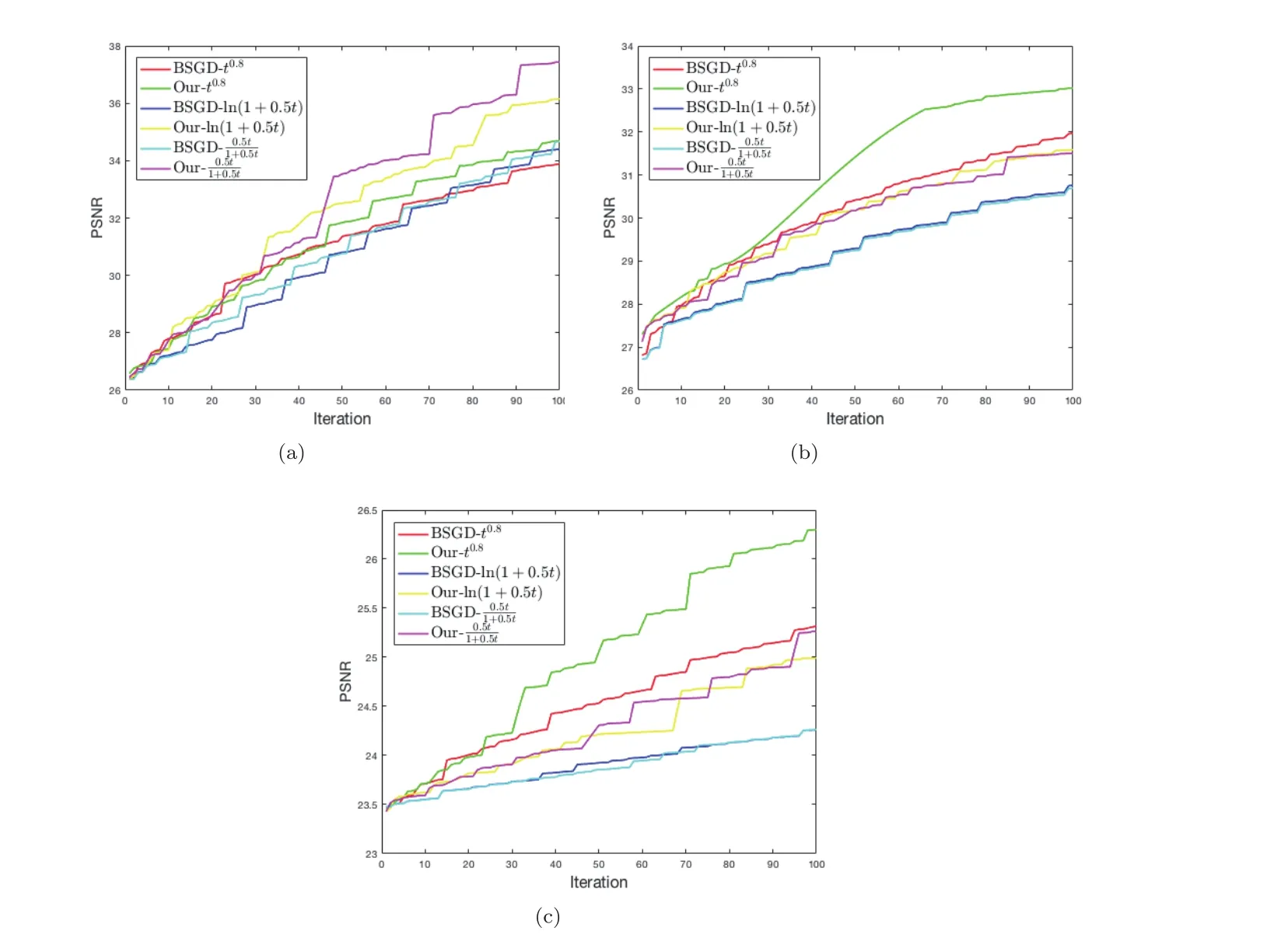
Figure 6 From left to right:The PSNR value of the recovered images by BSGD and the proposed algorithm versus iteration with three potential functions for “Shepp-Logan”,“NCAT” and “cerebral”.

5 Conclusion

In this paper,we proposed a smoothing inexact projected gradient descent with extrapolation to solve a class of constrained nonsmooth nonconvex minimization problems.The inexact projected gradient descent with extrapolation is applied to improve the performance of minimizing the corresponding smoothed nonconvex problem.Combined with a safe-guarding policy and adaptively updating the smoothing parameter,the proposed algorithm guarantees that any accumulation point of the sequence generated by this algorithm is an(affine-scaled)Clarke stationary point of the original nonsmooth and nonconvex problem.Numerical experiments and comparisons indicated that the proposed algorithm performed better visually and quantitatively than nonaccelerated gradient descent algorithms for the same model with or without box constraints for CT reconstruction problem.