高水头混流式水轮机减负荷瞬态流动特性研究
2022-12-05孙龙刚徐卓飞郭鹏程郑小波
孙龙刚,徐卓飞,郭鹏程,2,郑小波,2
(1.西安理工大学 水利水电学院,陕西 西安 710048;2.西安理工大学 省部共建西北旱区生态水利国家重点实验室,陕西 西安 710048)
1 研究背景
水电由于具有快速高效的启停响应,因而被用来调节电网容量及频率的动态平衡。近年来清洁能源在电网中占比持续提高,以风能和太阳能为代表的清洁能源的不定时并网对电网造成剧烈的不稳定冲击,此时水电机组必然经历快速且频繁的工况转换如减负荷过程以平衡电网参数[1-2]。水轮机运行模式的转变,通常伴随着回流、流动分离、空化、尾水管涡带、叶道涡、卡门涡等不稳定流动现象[3-6],从而在机组内部诱发具有繁杂幅频特征的压力脉动。高水头水轮机由于所受动态液体力更大,且水轮机减负荷过程中转轮对来流的不适应性增强,机组将承受更加复杂的不平衡作用力,由此产生的交变应力载荷会进一步加剧机组关键部件的疲劳破坏和磨损,缩短机组寿命,降低机组水力性能,从而影响电站的安全稳定运行[7-9]。因此,开展减负荷过程中高水头水轮机动态响应研究,对进一步促进水电与其他清洁能源的多能互补具有重要的现实意义。
模型试验与数值模拟是明确工况转换过程中水轮机内部不稳定流动特性及其诱发水力振动的重要手段。Trivedi等[10]试验研究了变转速工况下功率急速上升和下降过程中高水头混流式水轮机内部的压力脉动响应,发现动静干涉频率对应的压力脉动幅值在负荷变化期间相对较小,而在瞬态过程结束时提高了30倍。此外,快速启停策略下水轮机转轮叶片最大压力脉动幅值是缓慢启停策略幅值的1.5倍[11]。周勤等[12]通过数值方法研究水泵水轮机,发现甩负荷过程中转轮进口回流是不稳定压力脉动及不均匀湍动能生成的重要原因,叶片扭矩和径向力的最大幅值分别达初始值的10倍和60倍。Fu等[13]基于三维大涡模拟技术捕捉到水泵水轮机内部的异常低频压力脉动,研究发现该种压力脉动的诱发与水轮机内部水锤现象、转轮进口局部回流以及无叶区挡水环有关。基于一维管道与三维数值模拟耦合方法,陈秋华等[14]发现以部分负荷工况为初始工况,水泵水轮机飞逸过程中产生的转轮径向力和压力脉动相对额定工况更为剧烈。Goyal等[15-16]通过水轮模型试验发现,甩负荷过程中水轮机尾水管内形成的螺旋涡带可分解为表征轴向运动的突进模式和表征轴向运动的旋转模式,且突进模式比旋转模式提前出现,而增负荷过程中柱状涡带的形成主要受负荷变化过程中尾水管内驻点、反向流动及回流区的直接影响。Hosseinimanesh等[17]的研究显示,混流式水轮机运行在空载条件下,尾水管内部的轴向反向流动和周向切向流动之间交界面上出现的不稳定强剪切层,是造成涡结构破裂和压力波动向上游传播至转轮叶片的主要原因。Liu等[18]数值研究结果表明,水泵水轮机甩负荷过程中,尾水管壁面附近出现大量大尺度涡结构,引发低频压力脉动。Liu等[19]对原型水泵水轮机甩负荷条件下涡带的形成过程进行了分析,发现尾水管中的涡带出现在零力矩运行之前,随着流量的减小,尾水管中的涡带强度增加。作者前期研究显示[20-21],水轮机甩负荷过程中,尾水管内的涡旋强度显著提升,而飞逸过程中的能量耗散主要发生在转轮和尾水管内部。此外,Fu等[22-24]基于数值模拟方法研究了间隙、空化以及水声学对水泵水轮机工况转换过程的影响。
综上所述,水轮机工况转换会显著提升其内部的压力脉动幅值,且直接影响水轮机尾水管内的涡流结构形态及其演化过程。为进一步明确工况转换条件下水轮机特征参数的动态响应、水轮机内部压力脉动及涡流演化规律,本文基于动网格技术对一高水头混流式模型水轮机负荷减小过程进行了瞬态数值研究,分析了水轮机压力和速度演变规律、尾水管内涡流演化特性,并建立转轮轴向力与不稳定压力脉动之间的关联。
2 数值模拟策略
2.1 高水头模型水轮机本文以挪威科技大学(Norwegian University of Science and Technology-NTNU)公开的Francis99模型水轮机为研究对象,开展水轮机负荷减小过程的瞬态数值研究[25-27]。Francis99模型水轮机三维几何结构如图1所示,由进口至出口分别为带有14个嵌入式固定导叶的蜗壳、叶片数为28的活动导叶、由15个分流叶片和15个长叶片组成的转轮以及弯肘型尾水管。该水轮机模型与原型转轮出口直径分别为0.349 m和1.778 m,对应的原型机和模型机水头分别为12.0 m和377 m。图2所示为Francis99模型水轮机负荷减小过程中活动导叶开度随时间变化曲线,由图可知,负荷减小过程涉及到3种运行工况,分别为时段t=0至t=1.0 s,活动导叶开度为的9.84°的最优工况(Best Efficiency Point-BEP),时段t=3.5至t=10.0 s,导叶开度为6.72°的部分负荷工况(Part Load-PL)以及时段t=1.0至t=3.5 s,导叶开度由9.84°线性减小至6.72°的负荷减小过程(BEP to PL)。此外,整个负荷变化过程中,水轮机转轮的转速均为333.0 r/min。

图1 Francis99模型水轮机
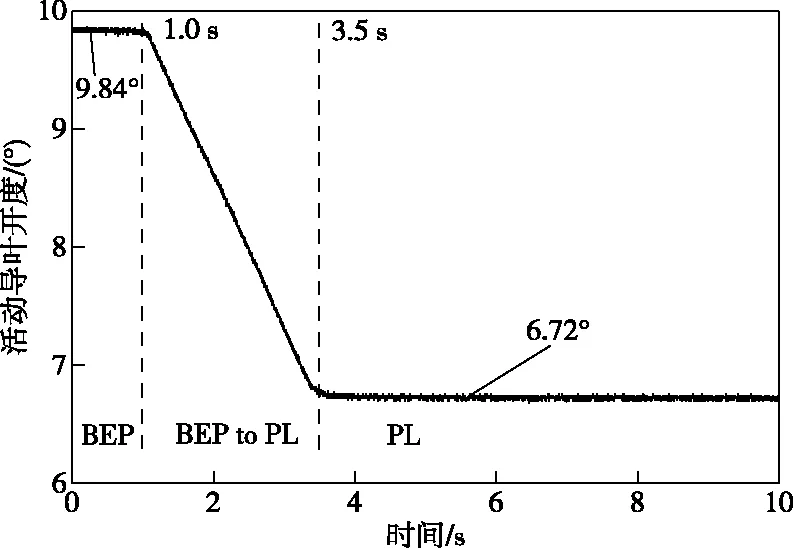
图2 活动导叶开度变化规律
为了对数值方法及模拟控制进行验证,NTNU提供了部分模型试验结果,其中压力及速度测量位置如图3所示[26-27]。图3中共布置了6个压力测点,其中VL02位于活动导叶与转轮之间的无叶区,用以捕捉动静干涉效应;转轮叶片压力面中间位置布置测点P42,出口侧靠近上冠处布置测点P71,用来分析转轮内部的压力脉动特征;同理,转轮叶片吸力面靠近上冠处布置测点S51;尾水管锥管段间隔180°布置了两个压力测点DT5和DT6,用来分析尾水管压力场随负荷变化规律。此外,试验中通过PIV(Particle Image Velocimetry)技术对尾水管锥管段3条线段L1、L2和L3进行了速度测量,其中L1与L2为垂直距离相差120 mm且与水轮机轴线垂直的水平线,其与x轴之间的角度均为79°;L3为与水轮机轴线重合的竖直线。速度测量中,对L1和L2上的28个位置进行测量,而L3上的测点数为19。

图3 压力与速度测点布置示意图
2.2 导叶网格变形控制水轮机工况转换是通过改变活动导叶开度进而控制水轮机流量来实现的,因此水轮机负荷改变数值研究中的一项重要内容为按照一定的导叶运动规律动态调整活动导叶的开度且保证一定的网格精度。为了实现上述目标,本文采用一种几何结构布尔运算与网格重构相结合的方法为活动导叶模拟域提供网格的自动更新,如图4和图5所示。当导叶开度变化时,导叶区域的网格发生变形,求解器按照预设的网格质量判断准则,确定是否执行网格重新划分。导叶运动过程中,网格质量判断准则为同时满足网格单元质量大于0.3且网格偏斜角小于85°。若不满足该条件,则首先获取当前时间步的导叶位置,然后经过导叶与背景区域两者之间的布尔运算获得新的导叶位置,最后以相同的网格设置参数进行网格重新划分。
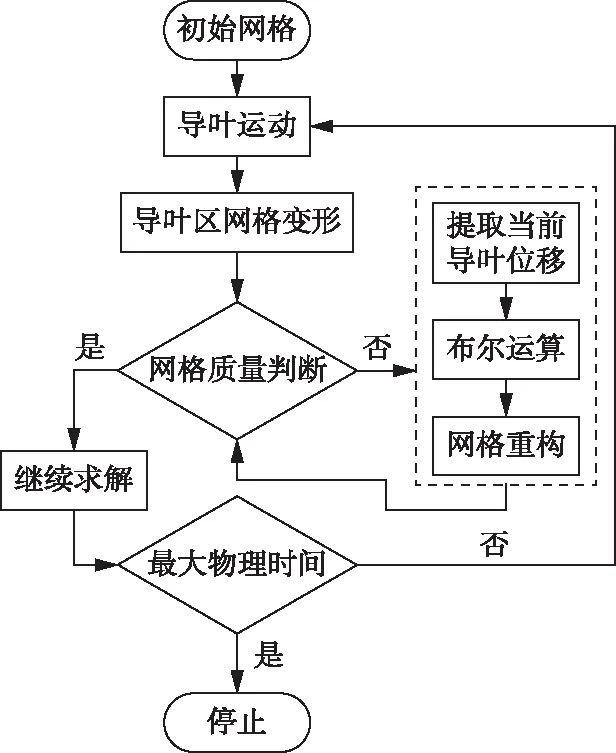
图4 导叶运动控制流程图
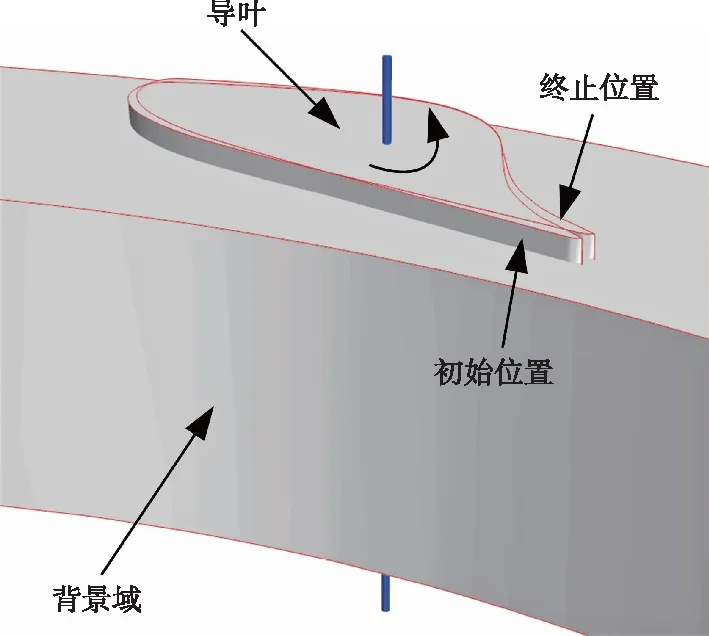
图5 活动导叶运动示意图
2.3 求解设置本文基于ANSYS Fluent进行水轮机负荷变化的数值计算,湍流模型采用SSTk-ω模型[28-29],该模型改进了近壁区低雷诺数流动的处理方式,能较好处理带有逆压梯度、流动分离的复杂流动问题。壁面边界层则采用全y+壁面函数处理方式,这种方式的优点在于使用混合壁面函数,对精细网格仿效低y+壁面处理,而对粗糙网格仿效高y+壁面处理。通过刚体运动来处理转轮域网格的旋转运动,所有壁面均设置为无滑移,对流项采用二阶迎风格式,时间离散则采用高精度的二阶格式,收敛标准设置为残差小于0.0001。按照Mössinger等[30]和Sotoudeh等[31]的研究,针对Francis99模型瞬态数值研究,瞬态时间步长设置为小于转轮旋转4°所用的时间能够获得较为可靠的数值结果。为了进一步提高数值精度,捕捉负荷变化过程中的压力脉动及涡流特性,本文采用对应于转轮旋转2°所用的时间,经计算瞬态时间步长为0.001 s,且每个时间步内迭代15次。首先进行BEP工况下的稳态计算,并以此为初场进行BEP工况下的非稳态计算,以转轮旋转4圈的非稳态计算结果作为负荷减小瞬态计算的初始值。数值计算进口给定总压,出口指定静压,这种边界条件的设置有效保证了数值计算与模型试验水轮机进出口压差的一致性。按照NTNU提供的进口静压P1、流量Q和净水头H的试验数据,可通过式(1)至(3)获得蜗壳进口总压Pin和尾水管出口静压条件Pout,
(1)
(2)
(3)
式中:P1为蜗壳进口静压,Pa;Pout为尾水管出口静压,Pa;Q为流量,m3/s;ρ为密度,取999.8 kg/m3;g为重力加速度,取9.82 m/s2;Ain为蜗壳进口横截面面积;Aout为尾水管出口横截面面积;vin为蜗壳进口速度,m/s;vout为尾水管出口速度,m/s;z为水轮机进出口高程差,m。
此外,本文对NTNU提供的进出口压力数据进行非线性曲线拟合处理,取其拟合结果作为瞬态模拟的进出口边界条件,如图6中点划线所示。
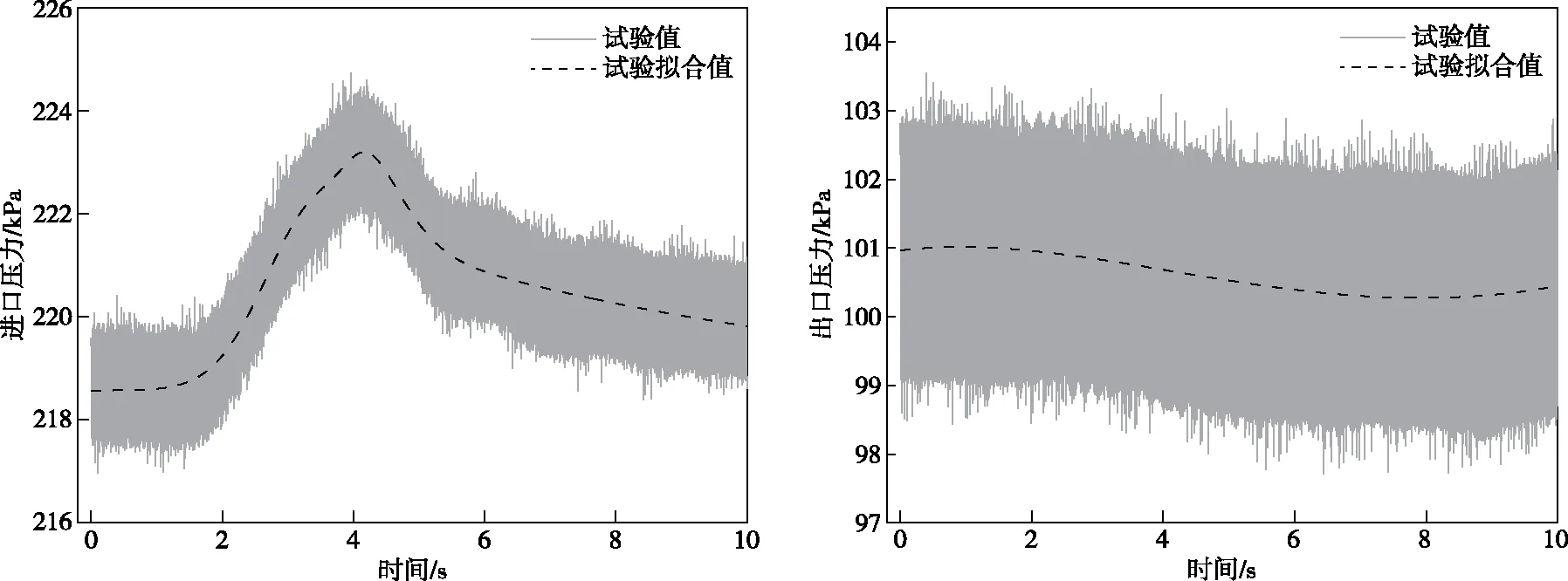
图6 进出口压力边界条件
2.4 计算域离散及网格无关性验证本文采用多面体网格对计算域进行离散,多面体网格的最大优点在于其一个控制体周围有大约10个相邻单元,因而能以相对较少的控制体获得更加精确的梯度和局部流动分离解[32-33]。图7所示为计算域网格示意图,其中固壁面如导叶、转轮叶片等通过棱柱层网格进行边界加密处理。
图7 计算域多面体网格示意图
为消除网格数量对计算结果的影响,本文采用美国机械工程师协会(ASME)推荐的网格收敛指数(GCI)进行网格离散误差的估计[34-36]。GCI是一个具有95%置信区间、表示两个对比网格中更密网格与渐进值之间距离的指标,并且预测进一步的网格细化对求解的影响。GCI网格无关性验证需要3套不同数目的网格,分别为细密网格(Fine)、中等网格(Medium)和粗糙网格(Coarse),计算的近似相对误差ea,外推相对误差eext以及网格收敛指数GCI:
(4)
(5)
(6)
式中:φ为计算所选择的关键变量;r为网格加密因子;p为采用定点迭代法计算的表观级数;下标1、2、3分别对应于网格方案Fine、Medium、Coarse;上标21和32分别表示网格Fine相对于Medium以及网格Medium相对于Coarse的计算值。
表1列出了BEP工况下数值计算离散误差的计算过程及结果统计。其中,N1、N2、N3为三种不同密度下的网格数,分别对应Fine、Medium和Coarse网格方案。本文选择水轮机水头H(单位为m)和转轮扭矩T(单位为N·m)作为网格无关性测试的关键变量。由表1统计结果知,三种密度网格的数值解以渐进形式收敛,表明网格加密有利于平均流场的求解。对Fine和Medium网格而言,计算的水头不确定度分别为0.072%和0.18%,转轮扭矩不确定度为0.066%和0.25%,表明Fine和Medium网格方案获得的数值解误差较小。为了平衡计算精度与计算资源之间的关系,本文最终选择了Medium网格进行数值计算,网格总数目为1451万,其中蜗壳和固定导叶网格数为292万,活动导叶为284万,转轮为514万,尾水管为361万。图8显示了Medium网格方案BEP工况转轮、尾水管的y+值分布云图,由图中可知,转轮壁面最大y+值为11.893,尾水管壁面最大y+值为7.061,且转轮壁面y+值主要范围在2.5以下,而尾水管壁面y+值主要范围在1.1左右,可以认为基本适用于SSTk-ω湍流模型。
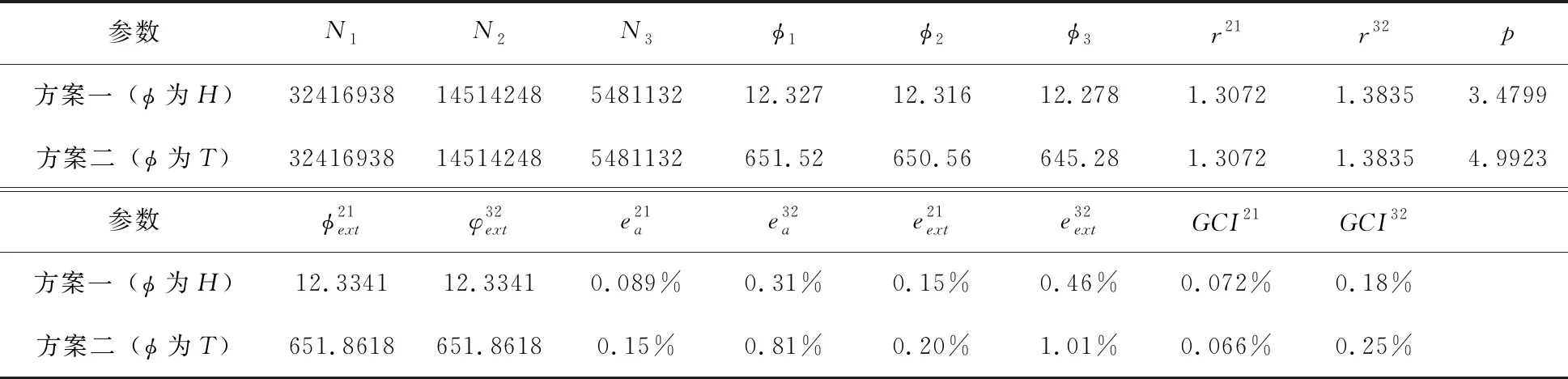
表1 数值计算离散误差及不确定性统计表

图8 转轮及尾水管壁面y+分布
3 结果与讨论
3.1 外特性分析为验证本文所采用数值策略的可靠性,图9显示了数值模拟与试验测试获得的水轮机外特性水头H和流量Q的对比结果。

图9 负荷减小过程水轮机水头与流量变化
图9结果显示,数值预测的水轮机水头与试验测试趋势平均值一致性较高。负荷减小过程中,水头在BEP工况下保持恒定,导叶闭合后,水头快速上升。t=3.5 s导叶停止闭合,水轮机开始运行在PL工况,此时水头继续上升,在t=4.2 s达到最高值,随后缓慢下降。水头变化结果表明,导叶的闭合对水轮机水头有一定的提升,且导叶停止运动后这种影响仍会在一定时间内持续。数值预测的流量与试验测试结果之间存在一定差异,数值结果显示为与导叶开度变化规律一致的线性变化,而试验值则为非线性变化规律,且导叶闭合过程t=1.0 s至t=3.5 s时段内,试验记录的流量值变化率小于数值结果。造成试验与数值之间差异的主要原因在于试验测试的流量计存在一定的时间延迟[27]。尽管数值解与试验测试存在一定差异,但可通过对比负荷减小过程中定导叶开度BEP阶段、PL阶段流量值与对应稳态试验测试结果之间的差异来量化本文数值流量结果的可信度。负荷减小过程中,BEP与PL工况数值计算获得的流量分别为0.193 24 m3/s和0.136 27 m3/s,对应稳态试验条件流量分别为0.199 59 m3/s和0.139 62 m3/s,仅仅相差3.2%和2.4%,表明数值计算的流量准确性较高。此外,水轮机流量调节是通过改变活动导叶开度实现的,流量变化趋势与导叶开度密切相关,本文中数值模拟与试验测试均显示了随导叶闭合流量逐渐减小的变化趋势,因此可认为本文数值计算的流量变化规律具有较高的可信度。综上所述,采用本文数值计算的模拟策略,能较好地反映负荷减小过程中水轮机外特性参数的动态响应。
3.2 压力脉动分析为进一步分析负荷减小过程中水轮机内部压力脉动特性,图10显示了无叶区和尾水管内VL02、DT5与DT6的压力脉动系数Cp,其中Cp为按照式(7)计算的无量纲数,
(7)

分析图10结果可知,数值模拟获得的无叶区压力脉动变化规律与试验测试结果吻合地较好,压力系数在定导叶开度BEP及PL工况下显示为均匀波动,而随着导叶的闭合压力系数线性减小。幅值方面,压力系数数值结果相对于试验值偏低,这与试验测试过程中的机械振动、电磁振荡以及数值模拟采用的网格、湍流模型和时间步长等有关。此外,由初始至终止时刻,数值模拟预测的压力系数幅值保持一致,而试验结果在负荷减小过程及PL工况下的压力脉动幅值要更高。
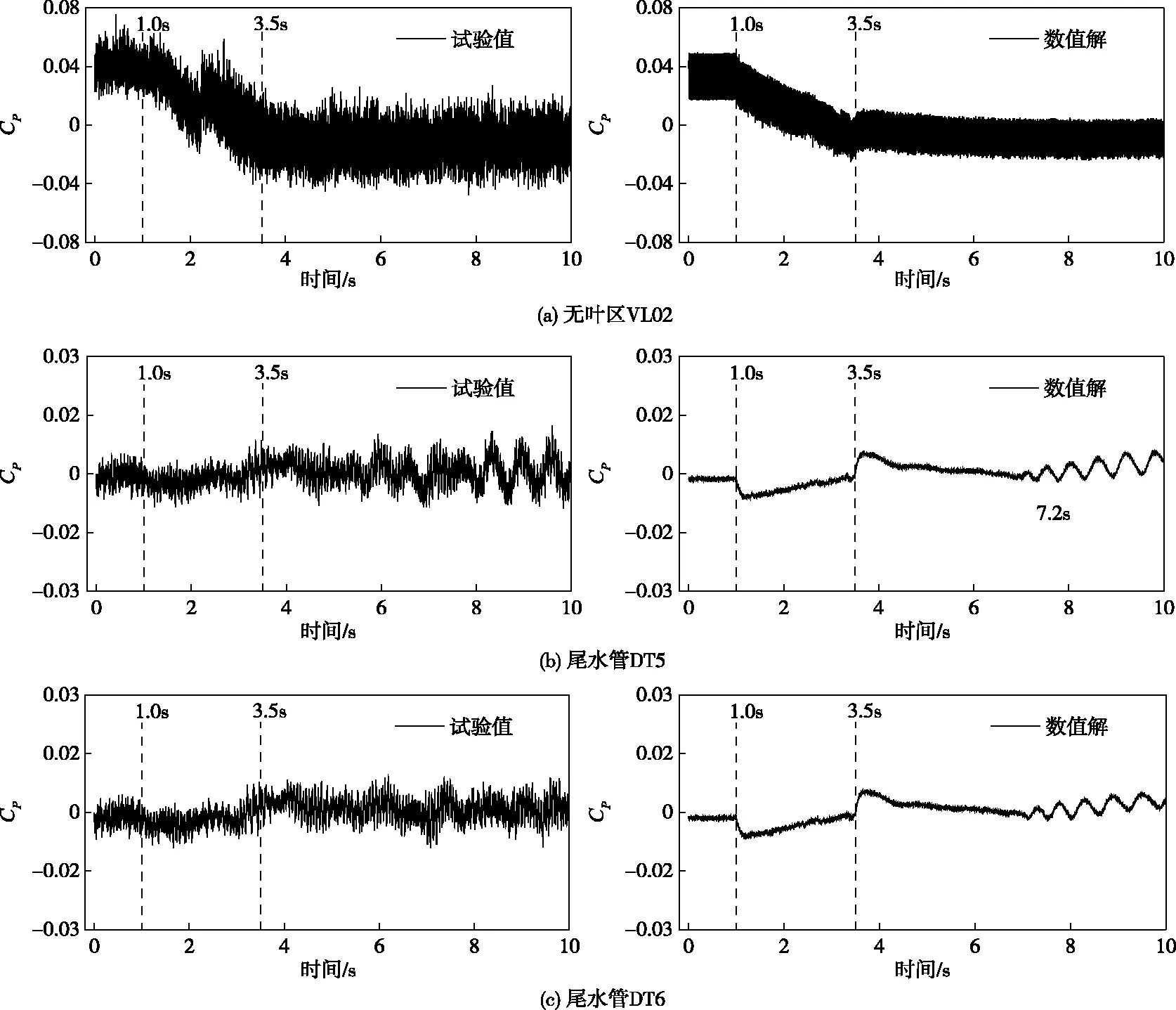
图10 数值与试验压力系数对比
尾水管内的压力系数结果显示,数值模拟低估了尾水管锥管段的压力脉动幅值,然而,其压力系数变化趋势与试验值一致性较高,因而在定性分析尾水管内的流动特性上具有较高的可靠性。BEP工况下,转轮出口接近法向出流,数值压力系数与试验压力系数平均值均保持为一个固定值,导叶闭合后,压力系数迅速下降,随后随导叶开度的减小逐渐增加。与BEP工况相似,导叶停止运动进入PL工况,压力系数首先迅速上升,随后缓慢下降,数值结果在时刻t=7.2 s以后出现一个显著的低频、高幅值周期性脉动,而相同的周期性脉动在试验过程中约在t=6.5 s后出现。低频、高幅值周期性压力系数的出现,与部分负荷工况下尾水管内螺旋形尾水管涡带的出现有关。
3.3 转轮轴向水推力分析轴向水推力不仅是水轮机组推力轴承载荷的重要组成部分,而且其脉动特性对会直接引起厂房结构的振动,因而是水轮机设计和运行过程中的一个重要参数[37]。为进一步分析轴向水推力相对水轮机负荷变化的响应关系,图11显示了负荷减小过程中水轮机轴向水推力随时间变化规律,其中正值表示数值模拟获得的轴向水推力与参考坐标系z轴方向一致。图中结果显示,BEP工况下轴向水推力绝对值最高且保持在一个常数附近。轴向水推力变化与导叶运动规律比较一致,即随着导叶的闭合而减小,且在导叶开始运动后,轴向水推力快速降低,而在导叶停止闭合后进入PL工况,轴向水推力首先快速上升,然后在一定时间范围内缓慢下降,最后做周期性脉动。
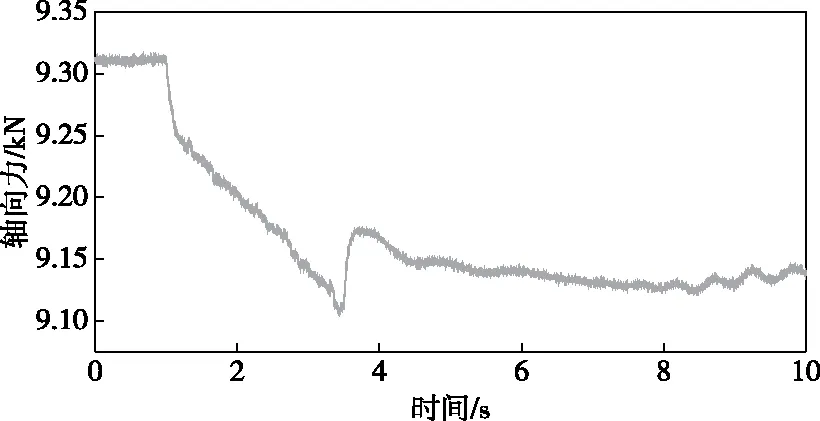
图11 负荷减小过程中轴向水推力随时间变化曲线
为确定影响轴向水推力的重要因素,本文通过相干分析方法建立轴向水推力与不稳定压力脉动之间的联系[38],如图12所示,图中分别显示了轴向水推力与无叶区测点VL02、转轮域测点P42以及尾水管测点DT6的相干系数。图12中横坐标f/fn定义为一个无量纲频率比,为计算频率f与水轮机转频fn之间的比值。纵坐标为相干系数,用来衡量两个变量之间的相关程度,相干系数越大,表明两个变量之间关联程度越高。分析图12可知,除较低频率范围及导叶、叶片通过频率28fn和30fn附近,轴向力相对于DT6的相干性系数均高于VL02和P42。相干系数大意味着两个信号之间的关联程度高,因此认为轴向力Fz与尾水管中DT6的压力脉动的相关度要显著高于无叶区和转轮内,表明尾水管内部非稳态压力波动向上游的传播是造成转轮轴向力波动的重要因素。
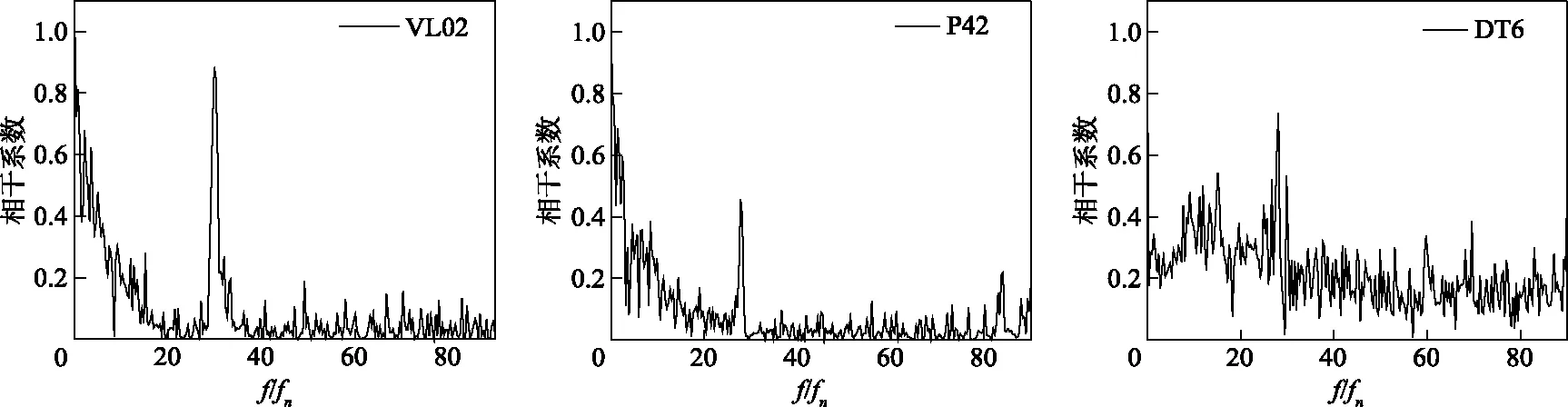
图12 轴向力与测点VL02、P42、DT6压力信号相关性
3.4 尾水管内速度变化情况分析螺旋形尾水管涡带的形成,与锥管段内的轴向速度及切向速度密切相关[39-40]。图13和图14分别为瞬态过程尾水管L1至L3上的轴向和切向速度分布,图中轴向速度沿z轴正向为负,切向速度沿转轮转向为正,图中横坐标r/r0定义为一个无量纲距离比,为速度测量线L1、L2、L3上坐标位置相对于该线段中间位置距离的比值。由于NTNU未提供切向速度数据,因此本文仅给出数值结果。为便于对不同工况的速度变量进行分析,本文将速度变化分为3个阶段,其中BEP工况为阶段Ⅰ,导叶开度变化过程BEP至PL为阶段Ⅱ,PL工况为阶段Ⅲ。
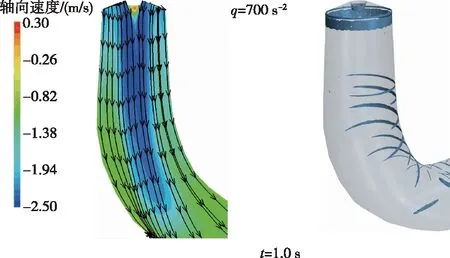
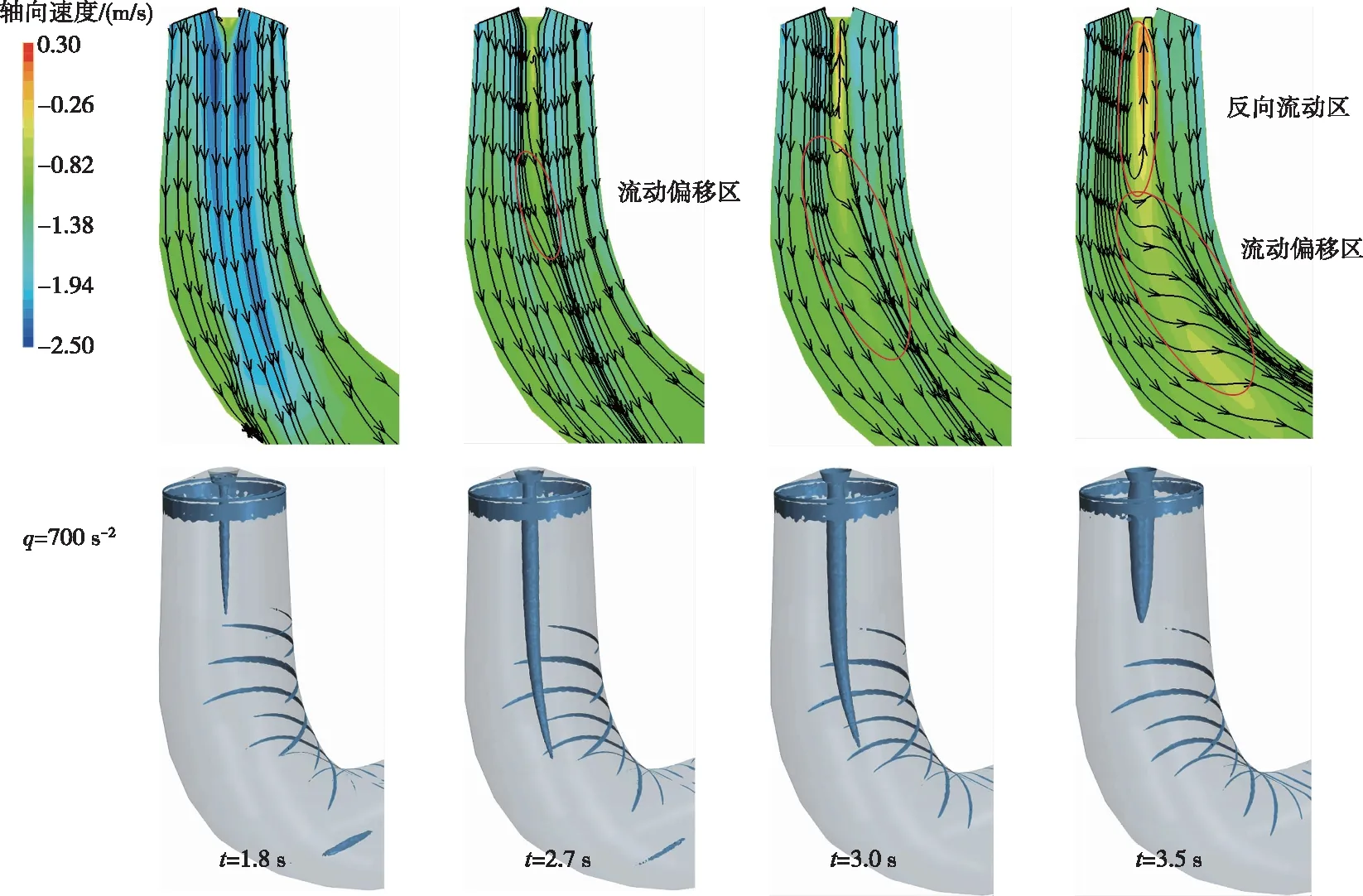
图13结果显示,水平线L1及L2上数值预测的轴向速度与试验结果比较吻合,竖直线L3上数值与试验结果存在一定差异,但二者之间的变化趋势比较一致。第Ⅰ阶段,转轮出口水流接近法向出流,轴向速度与主流方向相同,泄水锥下方L1与L2上的轴向速度高于尾水管锥管段壁面附近,而L3沿流向保持一致。导叶闭合的第Ⅱ阶段,L1与L2上测得的轴向速度在-0.5 图13 轴向速度分布 分析图14结果可知,L1与L2上的切向速度变化比较一致,在第Ⅰ阶段均与转轮转向一致,且转轴中心处绝对值较小。第Ⅱ阶段,转轴中心附近发生切向速度的反转,且随时间推移反向切向速度范围逐渐扩大。第Ⅲ阶段,转轴中心附近的正向切向速度区随导叶的闭合逐渐增加,而在这个正向速度区外侧,均显示为反向切向速度。之后,切向速度也表现以转轴为中心线,正向和负向交替出现的切向速度区。竖直线L3上的切向速度在第I和第Ⅱ阶段变化较小,而在第Ⅲ阶段后期切向速度出现方向的交替变化,且靠近转轮中心测点经历更多的切向速度方向变化。 图14 切向速度分布 3.5 尾水管涡带形成分析由BEP工况过渡至PL工况,水轮机尾水管内的压力、速度均显示了一定的低频振荡,这对尾水管涡带的形成有一定影响。为进一步深入理解水轮机负荷变化过程中尾水管内涡结构演化及尾水管涡带的形成过程,图15至图17分别显示了阶段Ⅰ至阶段Ⅲ尾水管内轴向速度云图、速度矢量分布及以Q准则显示的涡结构,图中Q准则阈值q=700 s-2,轴向速度为负时,表示轴向速度方向与参考坐标系z轴相反,与主流方向一致。由于BEP工况不同时刻尾水管内流场结构比较接近,因此本文只给出了t=1.0 s时刻的结果。 图15 阶段Ⅰ尾水管轴向速度及涡结构 图16 阶段Ⅱ尾水管轴向速度及涡结构 图17 阶段Ⅲ尾水管轴向速度及涡结构 图15速度分布结果显示,BEP工况下尾水管内为几乎与主流方向相同的纯轴向流动的稳定流场,轴向速度在锥管段中心附近较高,而在锥管段壁面附近较低。由于泄水锥的壁面效应,在其正下方出现范围较小的局部回流区。可视化涡结构等值面结果未出现自由涡结构,仅仅显示为附着于尾水管进口、泄水锥表面以及弯肘段的片状涡结构,这主要是由于固壁面附近速度梯度较高所致,而且这种片状涡结构在整个模拟过程的不同时刻均存在。因此,BEP工况下尾水管内流动光顺,未诱发不稳定涡结构。 第Ⅱ阶段,水轮机活动导叶由9.84°线性关闭至6.72°,水轮机流量逐渐减小,转轮进口冲角增大。分析图16结果可知,t=1.8 s,尾水管内的轴向速度由于流量的降低而减小,特别是转轴附近区域,此时水流方向仍然为轴向流动,未出现回流及分离区。然而,尾水管锥管段内出现了轴对称的自由涡结构,表明水轮机负荷的减小,激发了尾水管内部的不稳定流动。t=2.7 s,随着流量的减小,尾水管内的轴向速度进一步降低,锥管段出口与肘管段进口中心区域出现由肘管段外侧指向内侧的流动偏移区。此时,尾水管内的自由涡结构强度显著增加,由泄水锥延伸至肘管段进口处。导叶继续闭合至t=3.0 s,流动偏移强度迅速增强,其中轴向速度流线方向与尾水管轴线呈较大角度,其范围扩大至弯肘段中部。 此外,泄水锥下游出现反向轴向速度而形成回流区,此时的涡强度相对t=2.7 s有所增强,但仍然保持为对称结构。导叶终止闭合时刻t=3.5 s,尾水管内的轴向速度持续降低,流动偏移区域与回流区域范围均显著扩大,表明水轮机流量的减小使尾水管内的水力不稳定性进一步增强。然而,图16中显示的涡结构沿轴向迅速收缩,而在径向其涡核半径增加。综上所述,水轮机负荷变化过程中,尾水管内的轴向速度逐渐降低,诱发不稳定的流动偏移及形成回流区。可视化涡结构首先显示为强度较低的轴对称结构,随后涡强度沿轴向及径向均显著增强,最后沿轴向迅速收缩而沿径向强度增加,而在负荷变化的整个过程中涡形态均显示为对称结构。 第Ⅲ阶段,水轮机运行在定导叶开度PL工况下。t=3.7 s,尾水管内的轴向速度分布与t=3.5 s时刻比较接近,但转轴中心区域的回流强度提高且轴对称涡结构沿轴向收缩。t=5.5 s时,尾水管锥管段及弯肘段的低速区范围显著增加,对应地,尾水管内的流动偏移区域与回流区域范围被扩大,且在转轴中心左侧形成两个明显的漩涡。然而,相对于t=3.7 s,该时刻的自由涡强度被显著抑制,仅仅残留附着在泄水锥表面的部分涡结构。t=7.0 s,尾水管锥管段低速区内出现了多个漩涡区,涡结构强度较上一时刻显示了较大的差别,该时刻的涡强度有所增强,但涡形态演化为双螺旋状偏心结构。t=8.5 s,锥管段流态紊乱程度加剧,转轴中心的低速区不再关于尾水管中心线对称,其在尾水管内显示为“S”状,且靠近壁面的低速区处出现明显的漩涡结构,对水流形成一定的挤压作用而使壁面附近的速度提高。Q准则显示的涡形态为强度较高、单一的螺旋状偏心涡结构,为典型的部分负荷尾水管涡带,t=8.5 s之后,该螺旋状偏心涡带做与转轮转向相同的旋转运动且其形态保持固定。综合以上分析可知,PL工况下,尾水管内的回流范围显著增加,涡形态首先为轴对称形,然后沿轴向剧烈收缩,随后单一的柱状涡结构演化为强度升高的双螺旋状涡结构,最终该双螺旋状涡结构合并为单一的螺旋状偏心涡带并保持其形态。 本文采用基于多面体网格的动网格技术对Francis99高水头混流式模型水轮机负荷减小过渡过程进行了数值计算,分析了负荷变化对水轮机外特性参数、不同位置压力脉动及尾水管内涡流结构的影响,主要结论如下: (1)基于多面体网格技术和进出口压力边界条件的水轮机瞬态数值研究,能够较可靠地模拟负荷变化过程中水轮机水头、流量的变化规律。负荷变化过程中,无叶区压力信号变化趋势与导叶闭合规律一致。导叶闭合及停止运动的瞬间对尾水管压力信号有较大的扰动作用。导叶停止运动进入部分负荷工况,尾水管内逐渐产生低频周期性压力信号,且转轮轴向力与尾水管内压力脉动关联度最高,表明尾水管内的压力脉动向上游的传播是影响轴向水推力形成的重要因素。 (2)导叶闭合导致水轮机流量的降低,对尾水管内的横向流动及回流有一定的促进作用,加剧了尾水管内的不稳定流动。最优工况下,水轮机内部为光顺流动,尾水管内无自由涡结构。负荷减小过程中,尾水管内形成的强度较小的轴对称涡带结构,首先沿轴向拉伸,随后沿轴向剧烈收缩但径向尺寸增加。部分负荷工况下,轴对称涡带首先溃灭收缩,随后演变为附着在泄水锥上的双螺旋涡带结构,最后双螺旋涡带合并为单一的强度较高的螺旋形尾水管涡带。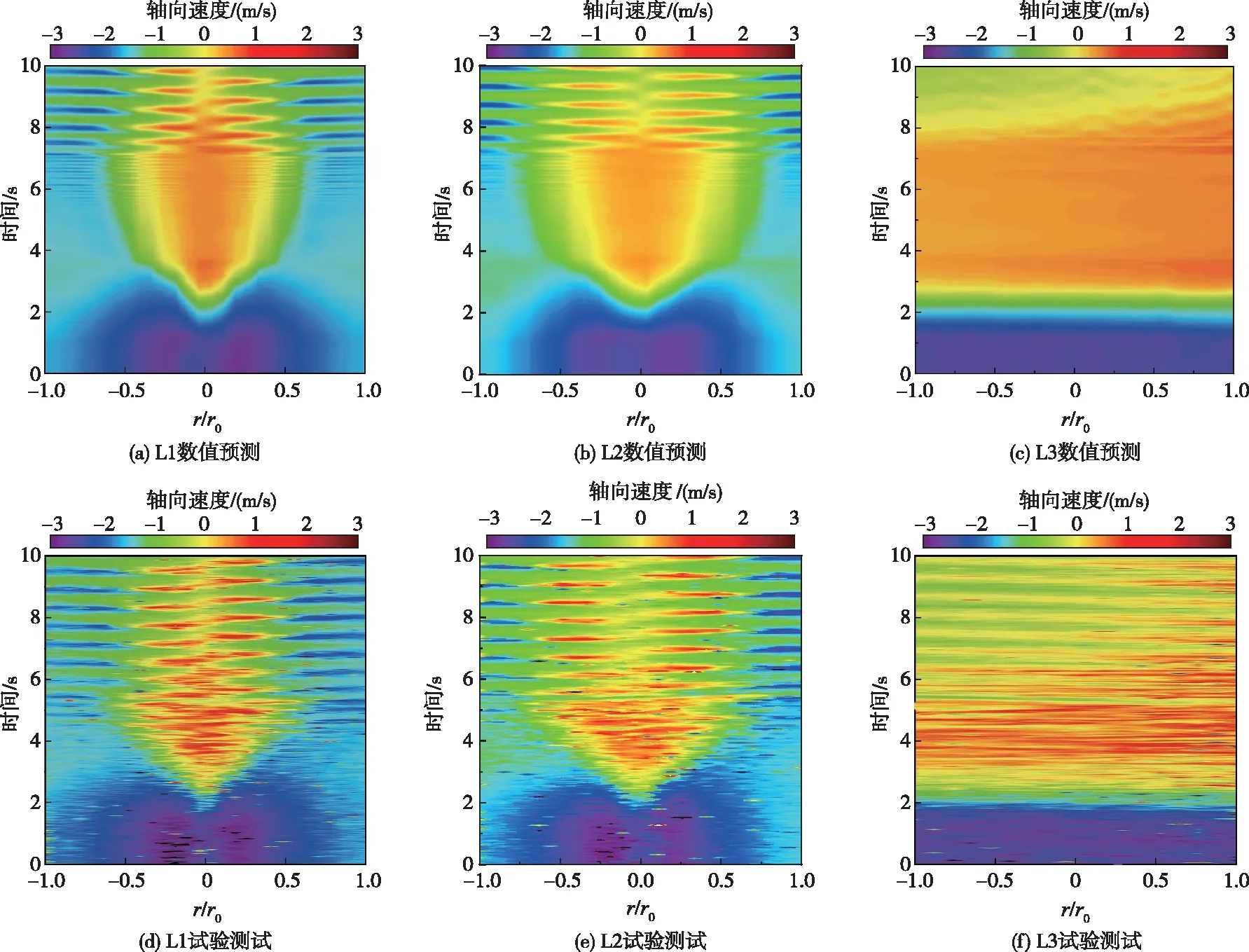


4 结论
