渡槽水体的热交换及水温和含冰率的时空变化

杨开林

(流域水循环模拟与调控国家重点实验室，中国水利水电科学研究院，北京 100038)

1 研究背景

渡槽是一种输水的混凝土水工建筑物，槽身多为板梁结构，过水断面一般采用矩形和U型。渡槽又称高架渠，通常架设于山谷、洼地、河流之上。与河渠不同，渡槽外表面裸露在大气环境中，除水面与大气热交换外，水体与内壁的热交换也受外壁与大气热交换的影响。在一般情况下，渡槽过水断面比连接渠道小得多，所以流速较大，冰期常常不封冻。这些导致寒潮时单位长度渡槽水温比相同过水能力渠道下降更快，而暖潮时单位长度渡槽水温比相同过水能力渠道上升更快。一旦受到严重寒潮侵袭，渡槽水温可能很快降低到0 ℃以下，成为产冰场，水体中产生大量冰花，导致渡槽下游渠道发生严重冰塞灾害，特别是当渡槽长度较大时。以南水北调中线输水工程为例，沿途修建了21座大跨度渡槽，最长渡槽长11 900 m，2016年1月21日受到极端寒潮侵袭，最低气温达-18.6 ℃，低温天气持续了3天，漕河渡槽(长2300 m)水温下降到0 ℃以下，产生了大量冰花，结果导致下游岗头隧洞前发生了严重冰塞险情[1-2]。因此，当分析长距离输水工程的冰情时，需要考虑渡槽水体与环境的热交换。

渡槽水体与环境的热交换包括水面与大气的热交换及水体与槽体的热交换。在水面与大气的热交换计算方面，目前一般采用国际著名冰工程专家Ashton[3]和沈洪道[4]的传统线性化模型，该模型只考虑气温和水温的影响，并在工程计算中得以普遍应用[5-6]。在水体与床底的热交换方面，Jobson[7]和茅泽育等[8]采用数值求解非稳态热传导偏微分方程的方法，研究了河床对水温的影响。河渠与大气的热交换非常复杂，仅仅考虑气温和水温的影响，常常不可避免会导致计算结果远远偏离实际情况。以南水北调中线工程为例，自2014年全线正式通水以来，在中线工程中进行了连续多年的冰情原型观测[1-2，9]，除2015—2016年度极端寒潮期冰情严重外，其它冬季以暖冬为主，主要冰情为岸冰、流冰，未形成持续冰盖，但是采用传统线性化热交换模型的计算结果却是形成连续冰盖及冰盖较厚[10-11]，与实际情况不符。鉴于此，杨开林[12-15]研究了冰期水面与大气及水体与床底的热交换模型，考虑了太阳辐射、地面与大气的长波辐射、水面蒸发和对流的热交换，以及热交换模型的线性化与水冰雪反照率的参数化，结果表明：(1)水面与大气的传统线性热交换模型仅适用于气候比较严寒地区封河期，例如我国东北，但不适用于我国华北地区，包括南水北调中线，因为这些地区冬季日平均气温常常大于-10 ℃；(2)水体与床底的热交换必须考虑。

虽然迄今冰期河渠水温模型的研究正在逐步完善，但是将其用来计算冰期渡槽水温不可避免的会与实际产生很大的偏差。河渠水温受床底地温的影响，而地温一般大于0 ℃。但是，由于渡槽架设空中，水温受渡槽外壁温度的影响，而外壁温度取决于外壁与大气的热交换，包括大气对流、外壁和大气的长波辐射、地表的长波辐射及太阳辐射，包括地表太阳辐射的反射等。换句话说，冰期气温常常小于0 ℃，所以渡槽外壁温度也常常小于0 ℃。存在的问题是目前在冰水力学中缺乏渡槽水体与槽体热交换模型方面的研究。

本文的主要目的是，基于太阳辐射理论、建筑物热过程和冰水力学基础理论，首先建立水体与渡槽的热交换参数化模型，然后研究冰期渡槽的水温模型，并分析水温和含冰率的时空变化规律。

2 水体与渡槽的热交换

下面将以图1所示矩形渡槽为例研究水体与渡槽的热交换，图中：B为水面宽，H为水深，hE，1和hE，2为边墙厚，hE，3为底板厚。

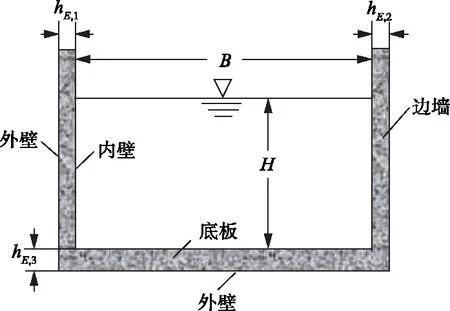
图1 矩形渡槽断面示意图

在冰期正常输水工况下，渡槽内水温一般分布均匀[9]。渡槽一般采用钢筋混凝土结构，一般由多层材料构成，当假设每层厚度均匀、热力条件是准稳态的且热量传递仅在平板竖直方向进行时，根据杨开林[14]的研究，水体与渡槽的热交换可通过多层固体平板的热传导来计算

(1)

(2)

式中：φwa为渡槽外壁的净热通量，W/m2；kE为边墙或底板的等效导热系数，W/(m·℃)；hE为边墙或底板的等效厚度，m；Ts为边墙或底板外壁的温度，℃；Tw为水温，℃；hj为边墙或底板第j层的厚度，m；kj为边墙或底板第j层的导热系数，W/(m·℃)；m为边墙或底板断面结构的层数；下标i=1，2，3分别表示渡槽两边墙和底板。

在一般情况下，两边墙和底板外壁的温度存在差别，其大小取决于外壁与大气的热交换，包括大气的对流、长波辐射、太阳辐射及地表的长波辐射和地表太阳辐射的反射等。

2.1 渡槽外壁与大气的对流热交换当渡槽边墙和底板是混凝土平板时，外壁与大气的对流热交换可描述为

φc，i=hc，i(Ts，i-Ta)，i=1，2，3

(3)

式中：φc为外壁的对流热通量，W/m2；hc为渡槽外壁对流热交换系数，W/(m2·℃)；Ta为气温，℃。

渡槽外壁对流热交换系数hc可利用凯尔别克的经验公式计算[16]

hc，i=3.67+3.83Va，i=1，2

(4a)

hc，i=2.17+3.83Va，i=3

(4b)

式中Va为风速，m/s。

2.2 渡槽外壁的长波辐射热交换渡槽外壁上的长波辐射包括外壁的长波辐射、大气长波逆辐射和地表的长波辐射[17]

φabθ，i=φa，i(φa-φb)+φg，i(φg-φb)，i=1，2，3

(5)

式中：φabθ为外壁上的长波辐射净热通量，W/m2；φa为大气的长波逆辐射热通量，W/m2；φb外壁的长波辐射热通量，W/m2；φg为地面的长波辐射热通量，W/m2；φa，i和φg，i分别为外壁对天空和对地面的辐射角系数。如果将渡槽外壁、地面和大气视为一个封闭系统，φa，i+φg，i=1.0。对于矩形渡槽边墙外壁，φa，i=φg，i=0.5，i=1，2；对于底板外壁，φa，3=0和φg，3=1.0。

外壁长波辐射φb和大气长波逆辐射φa可采用下述线性方程描述[13]

φab=φa-φb=φab0-hba(Ts，i-Ta)，i=1，2

(6)

式中：hba为外壁长波辐射的热交换系数，W/(m2·℃)；φab0为气温Ta的线性函数，W/m2，例如对河北保定地区[13]

φab0=-94.5-0.6Ta，hba=3.9

(7)

外壁长波辐射φb和地表长波辐射φg可由斯蒂弗-博尔茨曼四次方定律计算[3]

φb=σεwb(273.15+Ts，i)4，i=1，2，3

(8a)

φg=σεwg(273.15+Tg)4

(8b)

式中：σ=5.67×10-8W/(m2·K4)为斯特凡·玻尔兹曼常数；εwg为地表的黑度；Tg为地表温度，℃；εwb为底板外壁的黑度，对混凝土可取εwb=0.94。

当假设εwg=εwb，根据式(8a)计算可得如图2所示φb随Ts变化的关系曲线(点线)，采用线性回归的方法得

图2 长波辐射φb的线性回归

φb=305.14+3.89Ts，i，i=1，2，3

(9)

φg=305.14+3.89Tg

(10)

根据式(9)(10)可得

φg-φb=-hgb(Ts，i-Tg)，i=1，2，3

(11)

式中hgb≈3.9。

由于hgb=hba，把式(6)(11)代入式(5)得渡槽外壁上的长波辐射净热通量

φabθ，i=φa，iφab0-φa，ihba(Ts，i-Ta)-φg，ihba(Ts，i-Tg)，i=1，2，3

(12)

2.3 渡槽外壁与太阳辐射的热交换渡槽外壁的太阳辐射净热通量等于太阳直射、散射和地表反射净热通量之和，即

φcn=φDn+φdn+φRn

(13)

式中：φcn为外壁太阳辐射净热通量，W/m2；φDn为外壁太阳直射净热通量，W/m2；φdn为外壁太阳散射净热通量，W/m2；φRn为外壁接受的地表太阳辐射的反射净热通量，W/m2。

如图3所示，倾斜面上的晴天太阳直射[17-19]

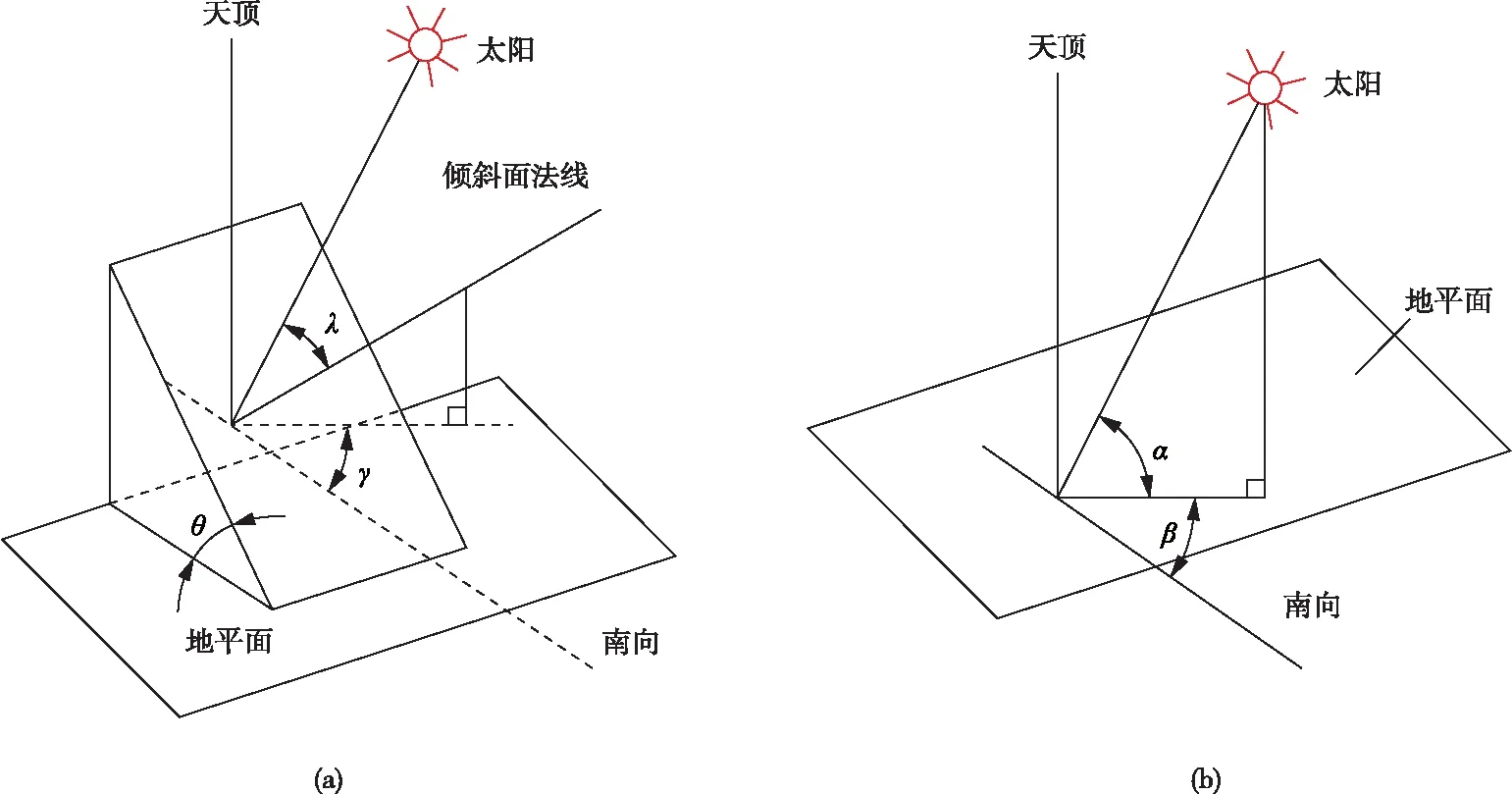
图3 倾斜面的太阳辐射示意图

φDθ=I0E0Pmcos(λ)

(14)

式中：φDθ为倾斜面上晴天太阳直射热通量，W/m2；I0=1367 W/m2为太阳常数；E0为日地距离订正系数；P为所有波长范围内的大气平均透明系数；m为光学大气质量；λ为太阳入射角，是太阳入射线与倾斜面法线之间的夹角。

太阳入射角λ与太阳高度角、倾斜面的方位角和太阳方位角的关系是

cos(λ)=cos(θ)sin(α)+sin(θ)cos(α)cos(β-γ)

(15)

式中：α为太阳高度角，rad；γ为倾斜面的方位角，rad，是倾斜面的法线在水平面上的投影与正南方向线的夹角，规定：面向东时为负，面向西时为正；β为太阳方位角，rad，太阳至地面上某给定点的连线在水平面上的投影与正南向(当地子午线)的夹角。

对于渡槽边墙，θ=π/2，由式(15)得

cos(λ)=cos(α)cos(β-γ)

(16a)

对于渡槽水面，θ≈0，由式(15)得

cos(λ)=sin(α)

(16b)

把式(16b)代入式(14)可得水平地表的晴天太阳直射计算公式。

根据式(14)(16)，考虑天气对太阳辐射的影响及边墙对太阳直射的反射，可得边墙外侧云天太阳直射净热通量[13]

φDn=(1-ac)(1-0.65C2)I0E0Pmcos(α)cos(β-γ)

(17)

式中：ac为边墙反照率，水泥砂浆抹面取0.32；C为云量，取值0～1，对晴天取0，而阴天取1。当边墙外侧面向正东时，则γ=-π/2而cos(β-γ)=-sinβ；当边墙外侧面向正西时，则γ=π/2而cos(β-γ)=sinβ。

太阳方位角β与观测地的地理纬度L、赤纬角δ和时角ω的关系是

(18)

当sin(β)>1，则

(19)

这时，β的正负由时角ω确定。赤纬角δ和时角ω的计算可参考文献[13]。

倾斜面上晴天太阳散射热通量[18-19]是

φdθ=φsdcos2(θ/2)

(20)

式中：φdθ为边墙晴天太阳散射热通量，W/m2；φsd为水平面上晴天太阳散射热通量，W/m2。

对于渡槽边墙，θ=π/2，考虑天气对太阳辐射的影响及边墙对太阳直射的反射[13]，可得云天太阳散射时边墙外侧净热通量

φdn=0.5φsd(1-ac)(1-0.65C2)

(21)

晴天倾斜面获得地面反射热通量是[17]

φRθ=aeφssin2(θ/2)

(22)

式中：φRθ为边墙接受的晴天地表反射净热通量，W/m2；ae为地表太阳辐射的反照率；φs为水平地表的晴天日射热通量，W/m2。

考虑云层对太阳辐射的影响及倾斜面对接受的地表太阳辐射的反射作用[13]，可得倾斜面接受的地表太阳辐射反射的净热通量

φRn=φRθ(1-ac)(1-0.65C2)

即

φRn=aeφs(1-ac)(1-0.65C2)sin2(θ/2)

(23)

对于矩形渡槽垂直边墙，θ=π/2，把式(17)(21)(23)代入式(13)得矩形渡槽边墙外壁太阳辐射净热通量

φcs，i=(1-ac)(1-0.65C2)(I0E0Pmcos(α)cos(β-γ)+0.5φsd+0.5aeφs)

(24)

式中下标i=1和2分别表示渡槽两边墙。在一般情况下，渡槽两侧边墙太阳辐射热通量存在差异。

对于渡槽底板，θ=π，影响外壁的太阳辐射只有地表反射热通量

φcs，i=ae(1-ac)φs(1-0.65C2)

(25)

式中下标i=3。草地的反照率ae=0.174～0.219，混凝土面的反照率ac=0.33～0.37。

式(24)(25)中水平地表的晴天日射和散射的热通量可采用下述公式计算[13]

φs=0.5(1+Pm)I0E0sin(α)

(26)

φsd=0.5(1-Pm)I0E0sin(α)

(27)

式(24)—(27)中太阳高度角α、日地距离订正系数E0、Pm的计算可参考文献[13]，因此对于给定位置的渡槽和云量C，φcs，i可计算得到。

下面以保定地区为例，了解水面与渡槽外壁太阳辐射的差异。假设有一矩形渡槽两边墙外壁分别面朝正东和正西，即上午只有面朝正东边墙外壁接受太阳直射，而下午只有面朝正西边墙外壁接受太阳直射。在此条件下，在上午，面朝正东边墙外壁太阳辐射包括太阳直射、散射和地面反射，而面朝正西边墙外壁太阳辐射只有太阳散射和地面反射；在下午，面朝正东边墙外壁太阳辐射只有太阳散射和地面反射，而面朝正西边墙外壁太阳辐射包括太阳直射、散射和地面反射。当太阳辐射时间与天文辐射相同、渡槽混凝土面的反照率ac=0.33、地表反照率ae=0.2、云量C取历史天气资料，则可得如图4所示保定地区2015—2016年冬季水面与渡槽外壁太阳辐射净热通量随时间的变化。图中：φsn为水面太阳辐射日平均净热通量，计算模型见下一节；φcs，1为上午渡槽面朝正东边墙外壁太阳辐射平均净热通量(等于下午渡槽面朝正西边墙外壁太阳辐射平均净热通量)；φcs，3为底板外壁接受的地表太阳辐射反射的日平均净热通量。

从图4可见，水面太阳辐射、边墙外侧太阳辐射和底板外侧太阳辐射的关系是φsn>φcs，1>φcs，3，晴天时φcs，1=170～280 W/m2，阴天时φcs，1有时小于100 W/m2；晴天时φsn=230～400 W/m2，阴天时φsn最小接近100 W/m2；φcs，3一般在50 W/m2左右变化。

图4 保定地区2015年12月—2016年2月冬季水面与渡槽外侧太阳辐射净热通量

2.4 渡槽外壁温度与气温的关系渡槽外壁与大气的热交换包括太阳辐射、对流和长波辐射，

φwa，i=φcs，i-φc，i+φabθ，i，i=1，2，3

(28)

式中φwa为外壁的净热通量，W/m2。

把式(3)(12)代入式(28)得

φwa，i=φcs，i+φa，iφab0-(hc，i+φa，ihba)(Ts，i-Ta)-φg，ihba(Ts，i-Tg)，i=1，2，3

(29)

联立求解式(1)(29)得

(Ts，i-Tw)kE，i/hE，i=φcs，i+φa，iφab0-(hc，i+φa，ihba)(Ts，i-Ta)-φg，ihba(Ts，i-Tg)，i=1，2，3

因为φa，i+φg，i=1，整理得渡槽外壁温度

(30)

上式适用于渡槽架于各种地表上，包括土石地面、水面、冰面和雪面等。

当渡槽架于土石地面上，包括地面积冰和积雪时，为使问题简化，一般假设地表温度接近于气温[17]，即Tg≈Ta，这时

(31a)

式中

(31b)

2.5 渡槽外壁的净热通量与气温和水温的关系把式(31)代入式(1)得渡槽外壁净热通量

整理得

φwa，i=hwa，i(φcs，i+φa，iφab0)/(hc，i+hba)+hwa，i(Ta-Tw)，i=1，2，3

(32)

hwa，i=1/[hE，i/kE，i+1/(hc，i+hba)]

(33)

式中hwa，i为渡槽外壁热交换系数，W/(m2·℃)。

当渡槽边墙和底板沿流动方向是均值平板时，则渡槽外壁的等效净热通量

(34)

(35)

式中：φwae为渡槽外壁的等效净热通量，W/m2；hwae为渡槽外壁的等效热交换系数，W/(m2·℃)；χ=χ1+χ2+χ3为渡槽湿周，m；χ1和χ2分别为两边墙的湿周，m；χ3为底板的湿周，m。

3 渡槽水温的时空变化规律

随着渡槽水体与周围环境的热交换，包括水面与大气的热交换与水体与渡槽边墙和底板的热交换，热量通过水流的运动和紊动向下游和整个过水断面传递，在一维条件下，沿流向的对流-热扩散方程是

(36)

式中：t为时间，s；x为距离，m；ρ为水的密度，kg/m3，ρ≈1000 kg/m3；Cp为水的比热，在0 ℃时Cp=4217.7 J/(kg·℃)；A为渡槽过水断面面积，m2；V为断面平均流速，m/s；Ex为热扩散系数；φsa为水面净热通量，W/m2；左边第一项表示过水断面热量随时间的变化；第二项表示过水断面热量随水体运动的变化，又称为热量的对流传递；第三项表示过水断面热量随水体热扩散的变化。

当水面净热通量φsa采用参考文献[14]线性化热交换模型时，则水面与大气的热交换与水体与渡槽边墙和底板的热交换可描述为

Bφsa+χφwbe=B(φsa0+hsa(Ta-Tw)-hsa2(Tw-Ta)2)+χ(φwae0+hwae(Ta-Tw))

(37)

φsa0=φsn-asa-bsaTa

(38)

式中：φsa为水面净热通量，W/m2；hsa为水面与大气的热交换系数，W/(m2·℃)；hsa2=0.158×10-3pa，pa为当地大气压，hPa；φsn为水面太阳辐射净热通量，W/m2；系数asa≫0和bsa>0，以保定地区为例，

asa=94.6+(6.04+2.95Vz)(1-Rh)c1≥94.6，bsa=0.6+(6.04+2.95Vz)(1-Rh)c2

(39)

式中：Vz为水面上1.5m的风速，m/s；Rh为大气的相对湿度；

在我国的北京、保定、沈阳、包头等地区，热交换系数可采用下式计算[13]

hsa=10.0(1.0+0.25Vz)

(40)

参考文献[12-13]，有

φsn=0.5I0E0sinα(1+Pm)(1-0.65C2)(1-as)

(41)

式中as为水面反照率

as=0.0564/α，α≥0.105

(42a)

as=0.537-4.408(α-0.105)，0≤α<0.105

(42b)

式(37)可改写为

(43)

式中：

(44)

在冰水力学分析中，水体热扩散项可忽略不计[3-4]。把式(43)代入式(36)，并采用特征线方法，式(36)偏微分方程可改写为

(45)

dx/dt=V

(46)

(47)

式中

(48)

式中：下标“i”为断面编号；m为断面数；Twp，i-1为渠段i进口时刻ti-1的水温， ℃；Twp，i为渠段i出口时刻ti的水温， ℃；Δti=ti-ti-1，s。由于系数r3，i>0总是成立，可得重要结论：在给定的气象条件下，水温Twp，i随着时间ti=t0+Δt1+Δt2+…+Δti的增加呈指数规律变化，逐渐趋近于系数-r1，i。

对式(46)积分并取一阶近似可得

Δti=Δxi/Vi

(49)

式中Δxi=xi-xi-1为渠段i的长度，m。

把式(49)代入式(47)消去Δti得水温的沿程分布递推计算公式，

(50)

据此，可得重要结论：在给定的气象条件下，水温Twp，i随离开进口距离xi=x0+Δx1+Δx2+…+Δxi的增加呈指数规律变化，逐渐趋近于系数-r1，i。

对于均匀流，在冬季寒潮情况下，如果参数a、b、c为常数，当令Twp=0，则由式(50)可得水温由渠道进口x0=0的温度Tw0下降到0 ℃的条件

(51)

4 渡槽含冰率的时空变化规律

当xp>xpc时，渡槽中将开始产生冰花。在一维流动条件下，如果水面没有漂浮冰块，则沿流向的渡槽冰花对流-扩散方程可描述为

(52)

式中：Ci=Ai/A为含冰率，表示单位长度渡槽中冰花体积与水和冰花总体积之比，其中Ai为过水断面A中冰花所占面积；ρi为冰的密度，kg/m3，一般取ρi≈917 kg/m3；Li为冰的潜热，在0 ℃时Li=3.33×105J/kg；Ei为冰花扩散系数。式(52)左边第一项表示单位长度渡槽中水和冰相变的潜热随时间的变化；第二项表示单位长度渡槽中水和冰相变的潜热随水体运动的变化，又称为热量的对流传递；第三项表示单位长度渡槽中水和冰相变的潜热随水体热扩散的变化；

在冰水力学分析中，热扩散项可忽略不计[3-4]。把式(43)代入式(52)，并采用特征线方法，式(52)偏微分方程可改写为

(53)

式中系数a、b、c与式(45)相同。

根据式(45)(53)可得

积分得

(54)

式中：下标“j”为从xpc开始的断面编号；ρCP/(ρiLi)≈0.0138。

根据式(54)可得重要结论：渡槽断面含冰率与负水温成正比沿程增加，负水温越小，水相变为冰的量越大；当水温由负转正时，水中冰将相变为水，含冰率将沿程减小。

5 算例

漕河渡槽是南水北调中线总干渠上的一座大型交叉建筑物，位于河北省满城县西北约9 km处，上游通过2000 m的总干渠与吴山隧洞衔接，下游通过750 m矩形干渠与岗头隧洞衔接。漕河渡槽全长L=2300 m，采用3槽一联整体多纵墙结构，简支梁式，单孔断面净宽6.0 m，槽高5.4 m。槽身底板厚0.5 m，边墙厚0.6 m。渡槽进、出口底高程为62.243～61.525 m。在2015—2016年冬季输水流量Q=45.72 m3/s，水深H=3.76 m，平均流速0.67 m/s。在2016年1月21—23日期间发生罕见寒潮，48小时内气温下降近10 ℃，实测最低气温-18.6 ℃，2016年1月23日，岗头隧洞进口出现严重冰塞，进口前两道拦冰索相继断裂，冰塞体整体下移，强烈撞击隧洞进口导墙，威胁隧洞节制闸安全。事后分析，主要由于上游长距离明渠内的大量流冰全部堆积在隧洞进口，形成较大体积的冰塞，顺流向长度约700 m，典型剖面结构可分为3层：上层为冰堆，厚20～40 cm，碎冰块堆积；中层为冰盖，厚25 cm，坚硬密实；下层为冰花，厚70～230 cm，絮状松散，具有一定阻水作用，渠道上游水位壅高0.4 m。岗头隧洞发生严重冰塞表明漕河渡槽中产生了大量冰花，水温Tw≤0 ℃。下面主要计算分析：1)风速和太阳辐射对渡槽外壁温度的影响；2)水体与渡槽热交换对水温和冰花沿程分布的影响。

原型观测漕河渡槽3槽内的水温分布均匀[9]，中墙对水温分布的影响可忽略不计，只需考虑水面和渡槽边墙和底板的热交换。

计算取大气相对湿度Rh=0.9，夜间Ta=-18.6 ℃，白昼Ta=-9.0 ℃和云量C=0.14，并假设渡槽进口水温Tw0=0.1 ℃。因水深3.76 m，边墙湿周χ1=χ2=3.76 m，3槽底板净宽χ3=3×6.0=18.0 m，渡槽断面湿周χ=χ1+χ2+χ3=25.52 m。边墙厚h1，i=0.6 m，底板厚h1，3=0.5 m，钢筋混凝土导热系数k1，i=1.74 W/(m·℃)，由式(2)得

保定地区纬度38°10′—40°00′，2016年1月23日上午，计算的渡槽面朝正东边墙外壁平均太阳辐射φcs，1=194.9 W/m2，面朝正西边墙外壁平均太阳辐射φcs，2=55.8 W/m2；下午，渡槽面朝正西边墙外壁平均太阳辐射φcs，1=194.9 W/m2，面朝正东边墙外壁平均太阳辐射φcs，2=55.8 W/m2；底板外壁的地表平均太阳辐射反射φcs，3≈44.5 W/m2。水面平均太阳辐射φsn=282.9 W/m2。

5.1 风速和太阳辐射对渡槽外壁温度的影响在上述计算条件下，可得如图5和图6所示渡槽外壁温度Ts与风速Va的关系曲线，图中：曲线1、2分别为两边墙外壁的Ts-Va，曲线3为底板外壁的Ts-Va。在夜间没有太阳辐射，两边墙外壁温度相同。在白昼，由于两边墙太阳辐射的差别，两边墙外壁温度差别较大，如图6所示。

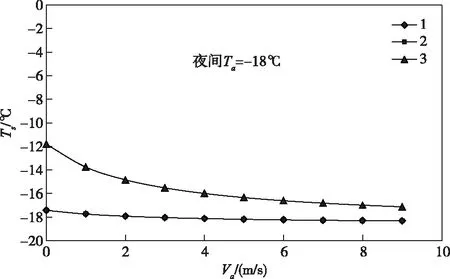
图5 夜间渡槽外壁温度随风速的变化

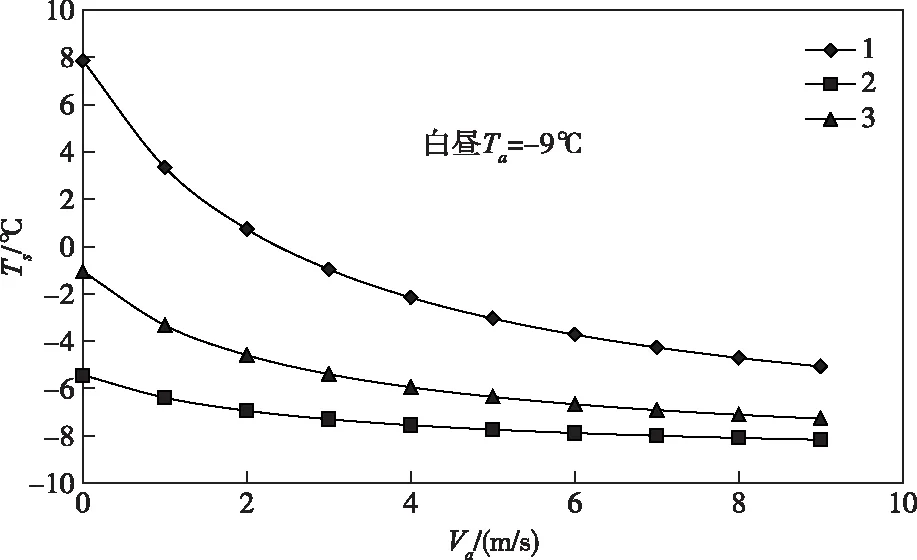
图6 白昼渡槽外壁温度随风速的变化

观察图5和图6，可得下述结论：

1)渡槽外壁温度随风速的增加而下降，特别是在0≤Va≤2 m/s区间下降较快；

2)在夜间，底板外壁温度高于边墙外壁温度较大，而边墙外壁温度接近于气温；

3)在白昼太阳辐射的影响下，渡槽两边墙外壁温度相差较大，而底板外壁温度介于两边墙外壁温度之间，同时朝阳面边墙外壁温度远远高于气温，特别是风速较小时，外壁温度随着风速的下降由负转正。

5.2 水体与渡槽热交换对水温和冰花沿程分布的影响当取风速Vz=Va=3.0 m/s，计算的渡槽夜间寒潮气温Ta=-18.6 ℃时水温沿特征线的变化如图7所示，显然，水温Twp随离开渡槽进口距离x的增加而近似线性下降，其中：曲线1考虑了水体与渡槽的热交换，水温由进口水温Tw0=0.1 ℃下降到0 ℃计算的临界长度xpc1=1954 m；曲线2没有考虑水体与渡槽的热交换，即取φwae0=0和hwae=0，对应xpc2=2273 m，两者相差较大，偏差相对值|xpc2-xpc1|/xpc1=16%。由于xpc1和xpc2小于渡槽长度L=2300 m，所以渡槽L-xpc1或者L-xpc2部分会产生冰花。在渡槽出口，对应xpc1的温度Twp1=-0.0012 ℃；对应xpc2的温度Twp2=-0.0018 ℃。根据式(54)，可得渡槽出口含冰率的偏差相对值|Cip2-Cip1|/Cip1=|Twp2-Twp1|/|Twp1|=50%。这一结果表明，在给定气象条件下，如果不考虑水体与渡槽热交换的影响，则计算的渡槽出口含冰率比实际含冰率少50%。从中可得一个重要结论：考虑水体与渡槽的热交换比不考虑的冰情严重得多，两者相差较大。

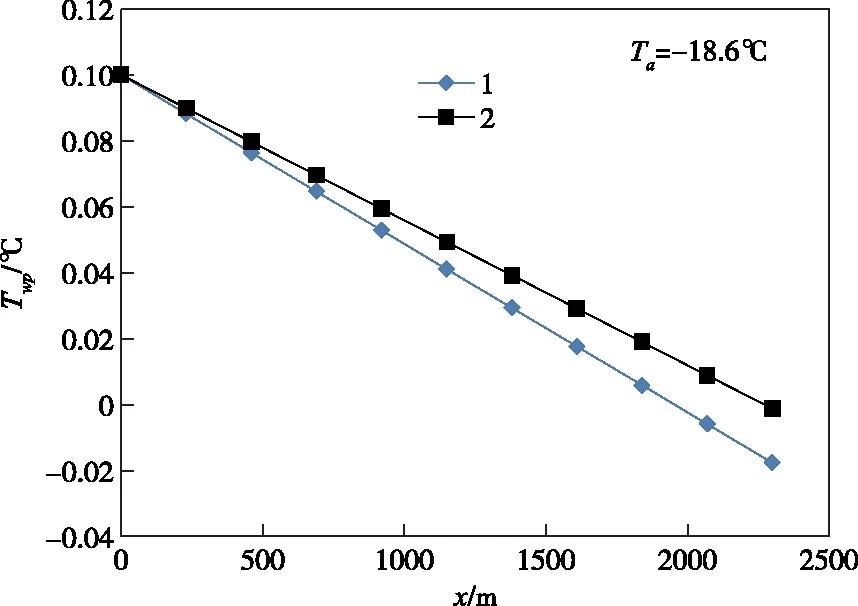
图7 夜间寒潮时渡槽水温沿特征线的变化

计算的白昼气温Ta=-9 ℃时渡槽水温沿特征线的变化如图8所示。由于白昼太阳辐射的影响，当渡槽进口水温Tw0=0.1 ℃时，水温没有下降到0 ℃，渡槽内不会产生冰花。此外，从图8可见，考虑水体与渡槽的热交换时渡槽水温沿特征线缓慢降低，但是不考虑水体与渡槽的热交换时渡槽水温沿特征线反而略微增加，两者偏差明显。

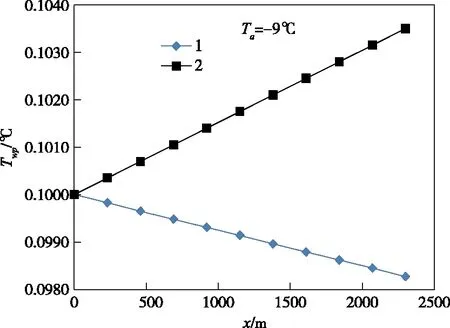
图8 白昼寒潮时渡槽水温沿特征线的变化

综上所述，可得一个重要结论：在寒潮期间，在渡槽中可能发生夜间产生冰花而白天不产生冰花的现象。需要说明的是，本算例水温和含冰率的计算结果是在给定渡槽进口水温的条件下得到的，不能完全反映真实的冰塞过程，只是说明考虑水体与渡槽边墙和底板热交换对正确模拟冰情的重要性。

6 结论

渡槽架设空中，水温不仅受水面与大气热交换的影响，而且受水体与渡槽热交换的影响。影响水体与渡槽热交换的主要因素是渡槽外壁温度。考虑渡槽外壁与大气的热交换，包括对流、外壁和大气的长波辐射、地表的长波辐射、太阳辐射及地表的反射等，本文提出了渡槽外壁温度的计算公式、水体与渡槽的热交换参数化模型、水温和含冰率的计算模型等。

通过研究，得出下述主要结论：

(1)渡槽外壁温度随风速的增加而下降，特别是在0≤Vz≤2 m/s区间；在夜间，底板外壁温度高于边墙外壁温度，且边墙外壁温度接近于气温；在白昼太阳辐射的影响下，渡槽两边墙外壁温度相差较大，而底板外壁温度介于两边墙外壁温度之间，同时朝阳面边墙外壁温度远远高于气温，特别是风速较小时，外壁温度随着风速的下降由负转正；

(2)在给定的气象条件下，水温随着时间和离开渡槽进口距离的增加呈指数规律变化；

(3)渡槽断面含冰率与负水温成反比沿程增加，负水温越小，水相变为冰的量越大；当水温由负转正时，水中冰将相变为水，含冰率将沿程减小；

(4)考虑水体与渡槽的热交换比不考虑的冰情严重得多，并且在寒潮期间，在渡槽中可能发生夜间产生冰花而白天不产生冰花的现象。