配水枢纽水力控制的仿真研究

李甲振，郭新蕾，殷峻暹，苏 岩，党康宁，王竞敏

(1.中国水利水电科学研究院 流域水循环模拟与调控国家重点实验室，北京 100038；2.陕西省引汉济渭工程建设有限公司，陕西 西安 710010)

1 研究背景

调水工程、大中型灌区是优化水资源空间配置、缓解局部地区或农业灌溉水资源短缺的工程措施，其安全调度、运行是保障工程效益正常发挥的关键[1]。工程的控制调节通常需要进行水力过渡过程计算，分析闸、泵、阀等设备一定操作策略下管涵渠隧的流量、水位、压力变化，使其满足规范规程、管道承压、设备限值等要求。

Joukowsky和Saint-Venant分别构建了有压输水系统和无压输水系统的控制方程[2-3]，为水力过渡过程计算奠定了理论基础。Wylie和Streeter的书籍[4]较全面地梳理和汇总了输水系统及典型构件的数学模型、求解算法等内容。对于某些典型工况，如明满交替水流，Song等[5]引入激波移动方程和交界面的特征线方程进行求解，Preissmann假设一条窄缝将有压、无压方程统一[6]，樊红刚等[7]提出了特征隐式格式求解算法；杨开林等[8]给出了解决隧洞首次充水问题的虚拟流动法。对于某些典型水工建筑物或系统布置，曹玉升等[9]建立了基于遗传程序结合水力学方法的过闸流量模型，张健等[10]提出了长距离供水管线设置空气阀的通用准则与相关公式，万五一等[11]给出了明渠—结合池—暗管输水系统中利用明渠特征线方法计算有压流的基本方程和建模过程。可见，针对一些典型、代表性的运行工况、建筑物或系统布置，仍需要研究分析其计算模型、求解方法等内容，以解决工程设计、运行调度等方面的实际生产需求。

配水枢纽是调水工程、大中型灌区一种常见的水工建筑物，用于连接长距离引水工程和配水工程的管涵渠隧、以及主引水渠(管)和配水干、支渠(管)。若使用水库作为配水枢纽，可视为常水位边界，引水工程和配水工程的水力过渡过程分别计算。受项目整体布局、地形地质条件、移民搬迁等因素的制约，很多工程没有合适的库区作为配水枢纽，需要人工修建池体。池体体积的确定一般参照以下规范：(1)GB 50265—2010《泵站设计规范》[12]规定：进水池的水下容积可按共用该进水池的水泵30～50倍设计流量确定；(2)SL 205—2015《水电站引水渠道及前池设计规范》[13]条文说明指出：大量工程的工作容积除以机组引水流量为50～300 s；(3)CECS 193：2005《城镇供水长距离输水管(渠)道工程技术规程》[14]规定：当输水规模不大或要求不高时，重力输水管道中间的水池容积可按不小于5 min的最大设计水量确定。可见，配水枢纽体积一般为30～300倍的设计流量。由于池体体积小，当供水流量或用户需求发生变化时，整个输水系统的沿程流量、水位、压力均会随之改变。将配水枢纽视作常水位边界则无法得到引水工程和配水工程真实的水力特性，不能适时、适量地调配水资源，极端情况可能造成漫堤溢流、爆管等事故。因此，部分输水系统的水力过渡过程特性，只有耦合引水工程、配水枢纽和配水工程进行仿真分析，才能得到准确可靠的流量、水位、压力数据，用于指导工程的调度运行。

本文的目的是研究有限容积配水枢纽复杂进出流条件下的控制方程、离散方法、计算程序等内容，建立数学模型，并结合典型算例对其水力控制进行仿真，解决引水工程、配水枢纽和配水工程耦合分析的模型问题。

2 数学模型

配水枢纽及其(部分)进、出水通常是具有自由表面的明渠流动，控制方程为圣维南方程组。求解方法包括有限差分法和有限单元法，其中，有限差分法的计算量相对较小，且隐式差分无条件稳定。因此，研究采用了应用较为广泛的Preissmann四点隐式差分格式。文献[15-17]均对离散方法、计算程序以及基本的水位、流量、水位—流量关系边界进行了详细介绍，此处不再赘述。下文将通过研究给出配水枢纽这一关键节点的控制方程、求解算法等内容。

图1示意了一种“一进、两出、一溢”的配水枢纽，渠道1的来水进入配水池，经闸门调控后分配给渠道2和渠道3；为避免溢流漫堤和排空水池，配水枢纽一般设置溢流道和放空管。溢流道、放空管均为水位—流量关系边界，本文以溢流道进行分析。

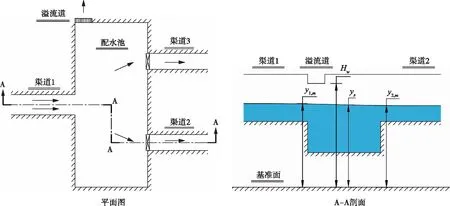
图1 配水枢纽示意(一进、两出、一溢)

2.1 控制方程渠道1的来水进入配水池，由非恒定流伯努利能量方程可得渠道1末节点与配水池的能量守恒方程

(1)

式中：y1，m为渠道1末节点相对于基准面的水面高度，m；下角标中1为渠道编号，m为渠道1划分的段数，计算节点编号为0～m；Q1，m为渠道1末节点的流量，m3/s；g为重力加速度，m/s2；A1，m为渠道1末节点的过流面积，m2；ys为配水池的水面高度，m；ζ1为水进入配水池的局部水头损失系数，包含断面变化、出水口、控制闸等。由于配水池的截面积一般远远大于渠道的截面积，配水池的流速水头可忽略。

配水池的水进入渠道2，由非恒定流伯努利能量方程可得配水池与渠道2末节点的能量守恒方程

(2)

式中：y2，n为渠道2末节点相对于基准面的水面高度，m；n为渠道2划分的段数，计算节点编号为0～n，从下游向上游编码；Q2，n为渠道2末节点的流量，m3/s；A2，n为渠道2末节点的过流面积，m2；ζ2为水进入渠道2的局部水头损失系数，包含断面变化、进水口、控制闸等。

配水池的水进入渠道3，由非恒定流伯努利能量方程可得配水池与渠道3首节点的能量守恒方程

(3)

式中：y3，0为渠道3首节点相对于基准面的水面高度，m；Q3，0为渠道3首节点的流量，m3/s；A3，0为渠道3首节点的过流面积，m2；ζ3为水进入渠道3的局部水头损失系数，包含断面变化、出水口、控制闸等。

配水池水体的增量等于进流、出流和溢流之和，质量守恒方程为

(4)

式中：A0为配水池的平面面积，m2；Qw为溢流道的流量，m3/s，计算公式为

(5)

式中：μ为流量系数；Bw为溢流堰宽度，m；Hw为溢流堰相对于基准面的堰顶高程，m。

2.2 求解算法式(1)采用牛顿-辛普森方法离散为

F10+e1Δy1，m+a1ΔQ1，m+esΔys=0

(6)

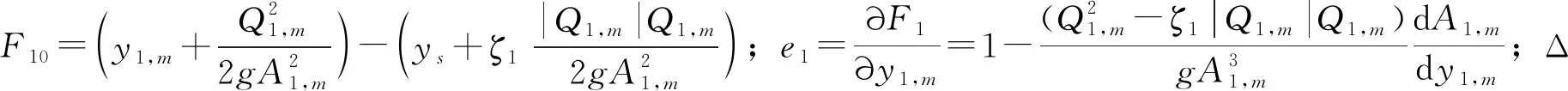
式(2)采用牛顿-辛普森方法离散为

F20+e2Δy2，n+a2ΔQ2，n+esΔys=0

(7)

式(3)采用牛顿-辛普森方法离散为

F30+e3Δy3，0+a3ΔQ3，0+esΔys=0

(8)

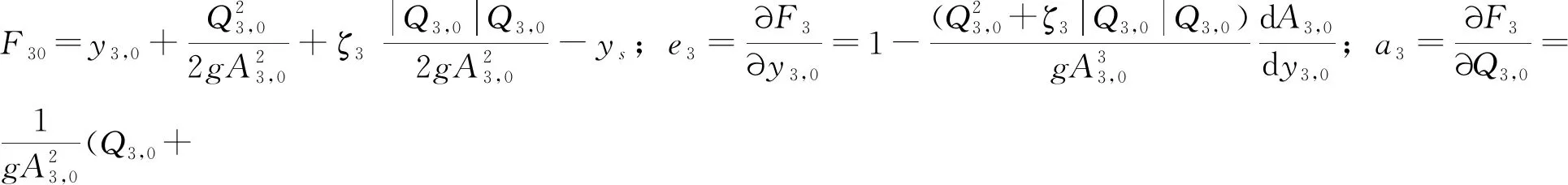
对式(4)积分并取二阶近似整理得

(9)

式中：Δt为时间步长，s；下角标0表示物理量前一时间步的数值。

采用牛顿-辛普森方法，式(9)可转化为

F40+F4，ysΔys+F4，Q1，mΔQ1，m+F4，Q2，nΔQ2，n+F4，Q3，0ΔQ3，0=0

(10)

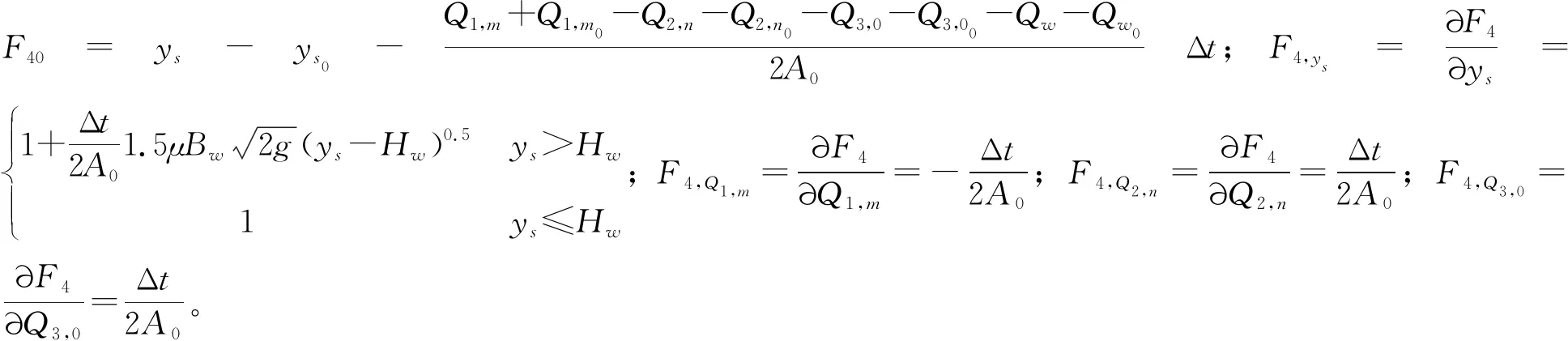
渠道1的进口通常是流量边界，通过Preissmann四点隐式差分格式对渠道1进行离散，并采用消元法进行变换可得

X=BX+P

(11)

ΔQ1，m=U1，2mΔy1，m+P1，2m

(12)

类似地，渠道2的出口为水位边界或水位-流量关系时，由出口向进口方向消元可得

Δy2，n=U2，2nΔQ2，n+P2，2n

(13)

由式(6)得

(14)

式(14)代入式(12)得

(15)

由式(7)得

(16)

式(16)代入式(13)得

(17)

式(15)和(17)代入式(10)得

(18)

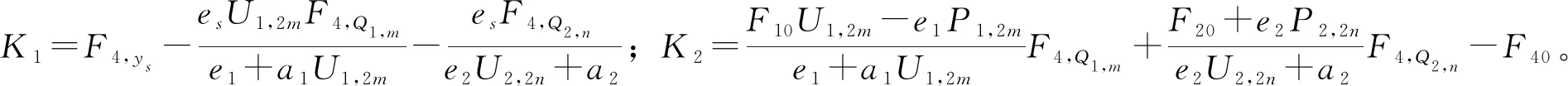
式(18)代入式(8)得

b3，0Δy3，0+c3，0ΔQ3，0=D3，0

(19)

对整个输水系统进行数值求解时，某一迭代步的计算程序为：

(1)利用双扫法的消元过程计算渠道1和渠道2的矩阵B和列向量P的元素U1，i、W1，i、P1，i、U2，j、W2，j和P2，j(i=0，1，…，2m，j=0，1，…，2n)；

(2)利用式(19)确定渠道3进口边界的双扫法系数，b3，0、c3，0和D3，0；

(3)用双扫法的回代过程求解渠道3各计算节点的水位增量和流量增量；

(4)利用式(18)、(17)、(16)、(15)和(14)依次求解Δys、ΔQ2，n、Δy2，n、ΔQ1，m和Δy1，m；

(5)利用双扫法的回代过程求解渠道1和渠道2各计算节点的水位增量和流量增量。

当配水池具有M个进水、N个出水时(M、N为任意正整数)，控制方程包括M个进水与配水池的能量守恒、配水池与N个出水的能量守恒以及水体的质量守恒方程，可参照式(1)—(5)，方程数量为M+N+1。求解方法与“一进、两出、一溢”配水枢纽类似，即，利用双扫法的消元过程计算M个进水和N-1个出水末节点的水位增量与流量增量关系；结合推求的M+N+1个控制方程，求解第N个出水首节点的水位增量与流量增量关系；利用回代过程求解第N个出水所有节点的水位增量与流量增量；求解其他渠道所有节点的水位增量与流量增量。当某些进水或出水是有压流动时，可采用窄缝法进行求解。即假设管道顶部有一条非常窄的缝隙，既不增加管道的截面积，也不增加水力半径，宽度为[17]

B=gA/a2

(20)

式中：B为缝隙宽度，m；A为有压流动的截面积，m2；a为水击波速，m/s。

2.3 模型验证青草沙水库的原水通过2根长13 650 m、直径5.5 m的输水隧洞输送至五号沟泵站前池，继而向下游各用户配水。某次水泵调试运行时，停泵0.5 h后再次开泵，李静毅等[18]观察到配水池异常的水位波动，振幅高达1 m。本文对该过程进行了仿真计算，关键参数如表1所示。

表1 关键参数

仿真计算的水位波动、峰谷值和周期与现场实测结果一致，如图2所示，说明模型能够较好地模拟配水池的水力过渡过程特性。

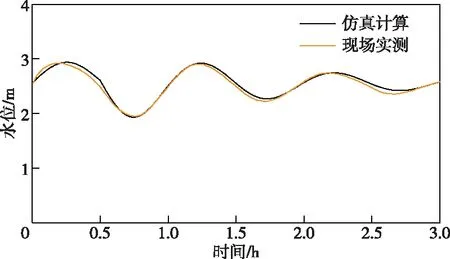
图2 仿真计算与现场实测对比

3 计算实例

引汉济渭工程通过越岭隧洞将三河口水库的水输送至黄池沟配水枢纽，配水工程将黄池沟的水通过南干线和北干线输送至渭河两岸的21个受水对象，如图3所示[19-20]。黄池沟为矩形池体，长105 m、宽35 m、深8.43～10.59 m，容积为2.2万 m3。越岭隧洞、南干线、北干线的设计流量分别为70 m3/s、47 m3/s和30 m3/s。越岭隧洞输送设计流量70 m3/s时，南干线、北干线的配水流量存在47 m3/s+23 m3/s、40 m3/s+30 m3/s两种情况。配水流量调节时，越岭隧洞、黄池沟、南干线和北干线的流量、水位变化，是工程调度关注的核心，也是本文模型需要解决的问题。输水隧洞参数、系统的边界条件、初始条件如表2所示。

图3 工程布置图

表2 计算实例的关键参数

配水枢纽和配水工程的水力过渡过程特性如图4所示。南干线5 km、10 km处分别在闸门动作103 min和136 min后，达到目标流量40 m3/s；上黄池在闸门动作15 min后，达到目标流量30 m3/s。黄池沟水位由514.88 m平稳地降低为514.74 m，南干线闸后水位由514.33 m降低为513.78 m，上黄池水位由512.79 m增加为514.10 m。黄池沟上游越岭隧洞的水力过渡过程特性如图5所示。上游5 km处的流量先增大至70.14 m3/s，之后缓慢恢复至70.00 m3/s，水位由516.84 m降低至516.79 m。黄池沟上游15 km范围内越岭隧洞的流量和水位均随之变化，变化幅度随距离的增加而减小。根据拟定的控制策略进行操作，越岭隧洞、南干线、北干线的流量平稳过渡，明流隧洞未出现满流，黄池沟也未发生溢流。

图4 典型位置的流量和水位过程

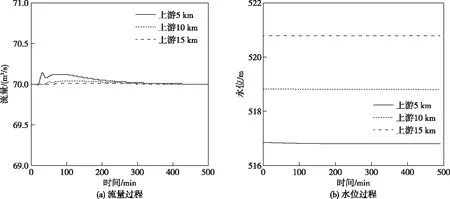
图5 黄池沟上游越岭隧道的水力特性

若将黄池沟配水枢纽作为常水位边界，越岭隧洞的沿程流量和水位则不会发生任何改变，南干线或北干线的调节也不会对另一条干线的运行造成影响。显然，这与实际情况是完全不符的。对于其他控制策略或布置有限容积配水枢纽的其他工程[21-23]，需要具体问题、具体分析，论证引水工程和配水工程的水力过渡过程是否可以单独分析，而不能简单地将配水枢纽作为常水位边界考虑。

4 结论

本文针对有限容积配水枢纽的数学模型进行研究，以“一进、两出、一溢”的布置型式作为典型代表，给出了能量守恒、质量守恒方程，以及基于Preissmann四点隐式差分算法的计算程序。对于实际工程中可能碰到的多进水、多出水布置，给出了求解过程；对于进水或出水为有压流的工况，给出了窄缝法的求解思路。

引水工程和配水工程的水力过渡过程现阶段一般单独计算，中间节点选择配水枢纽，控制水位为设计水位。但该方法并不对所有的长距离调水工程和大中型灌区都适用，特别是类似引汉济渭布置型式的水利工程，某条配水支线的流量调节会引起其他配水支线以及引水干线水力特性的显著变化，引水干线的调度需要同步调整所有支线。对于类似布置的水利工程，运行调度方案需要根据整个输水系统的水力过渡过程计算结果进行编制。本文建立的配水枢纽数学模型，则为上述问题的解决提供了一定的理论依据。利用本文提出的数学模型和求解方法，可对于类似布置有限容积复杂配水枢纽工程耦合系统的水力过渡过程特性进行分析和运行调度方案编制，亦可用于配水枢纽前期设计参数的选择。