医学生物学引入数学图像的教学研究

王 珏，吴 娜，张育敏，胡丽丽△

(1山西中医药大学基础医学院生物学系，晋中 030600；2山西中医药大学基础医学院实验教学中心；3山西中医药大学基础医学院基础医学系；△通讯作者)

医学生物学是中医药院校医学生的必修基础课，课程内容以细胞学和遗传学两部分为主，帮助学生认知生命的本质规律，是基础医学与临床医学的桥梁，为后者的深入研究奠定理论基础[1]。其中医学遗传学部分涉及内容广，知识量大，医学生较难掌握[2]。目前该部分的教学难点表现为两个方面：①由于医学生中大于50%的学生是文科生源(高考选择文科)，因此学生对涉及数学规律和计算的遗传学内容存在抵触情绪，学习信心不足影响了知识的理解吸收；②教师授课时对内容的讲解多数停留在表面的已知规律，对教材中出现的数学结论推导过程重视度不够，导致学生普遍通过死记硬背区分不同的遗传方式，而忽略了对遗传规律的理解和探索。实际上，数学思维的培养与合理应用是提高学生思维能力的重要途径[3，4]。然而这部分内容却是教师和学生常忽略甚至刻意避免的。因此，从本质(数学相关内容)入手，去解决目前出现的教学问题，应是提升课堂效率，提高学习效果的主要方式。我们在课程建设的过程中，提出应正视并重视医学遗传学部分出现的数学内容，以深入分析、解析逻辑、巩固推算、拓展应用的原则对课程知识进行重塑。

教学使用教材为王望九老师主编的《医学生物学》(全国中医药行业高等教育“十三五”规划教材)。其中医学遗传学内容涉及的数学问题如下：推算家族后代单基因遗传病的发病概率；比较质量性状与数量性状、遗传病复发风险与亲属级别的关系；遗传平衡群体相关理论及应用等。针对以上内容，我们提出通过数学统计饼状图分析单基因遗传病的患病率；通过数学集合思想的应用比较质量性状和数量性状；通过数学坐标曲线的绘制探索遗传平衡群体的特征。教学改革引导学生合理应用数学方法去解决医学遗传学问题，加强学生对科学问题归纳概括、演绎推理的能力。

1 研究对象及方法

1.1 研究对象

研究对象为2019级本科生。教师主要在中医学专业第三学期的医学生物学第二篇内容医学遗传学课程教学中，融入数学图像的应用教学。

1.2 研究方法

1.2.1 教学过程引入数学图像 教师根据不同章节内容，将数学图像合理应用，具体操作包括两方面：①准备教学阶段，教师通过文献阅读进行知识积累，选择合适的数学图像，进行应用检验，换位学生角度思考；②实践教学阶段，教师坚持引导为主，引入数学图像的应用，加强学生思考维度，使课堂教学起到抽丝剥茧、直至真理的效果。

1.2.2 考核过程引入数学图像 教师设立完善的教学效果评价体系，例如试题中出现数学图像的表现形式，考查学生对课堂构建的数学图形的理解和应用以及学生运用数学思想对新问题的分析和判断能力。以百分制试卷为例，此部分内容不低于25分。此外，教师结合课堂师生互动、课后问卷调查等方式综合评价教学内容改革设计的效果。

2 研究结果

2.1 饼状图分析单基因遗传病后代患病概率

单基因遗传学围绕孟德尔遗传定律展开。单基因遗传病种类多，特征复杂，学生推算后代患病率时会逻辑不清，混淆出错。据此教师引入数学统计图形中的饼状图，将个体产生配子直观显示，再通过组合、衍变的方式，最终得到后代不同基因型的比例，见表1所示。

如表1中各图形所示，饼状图描绘基因概率的核心方法是在衍变过程中使配子跟随箭头的方向进入相应区划领域。这种方式体现了简单条理的思考过程，并通过面积大小对概率有更直观的表达，很大程度上也提高了文科生源学生对知识的接受度。另一方面，教师引导学生分析最后的饼状图面积，也可得到一些经典结论：对于常染色体显性遗传病，亲代有一方是患者时，后代患者占比高于正常个体，这也说明了致病基因在人体遗传过程中的危害；对于常染色体隐性遗传病，当亲代中有携带者，后代中会出现携带者或患者，这种现象是遗传负荷中的分离负荷，会降低群体的适合度；对于X-连锁显性遗传病，女性患病概率高，而对于X-连锁隐性遗传病，男性患病概率高。通过数学图像的应用，我们可将种类繁多、较为复杂的问题统一，并深化了课程内容。

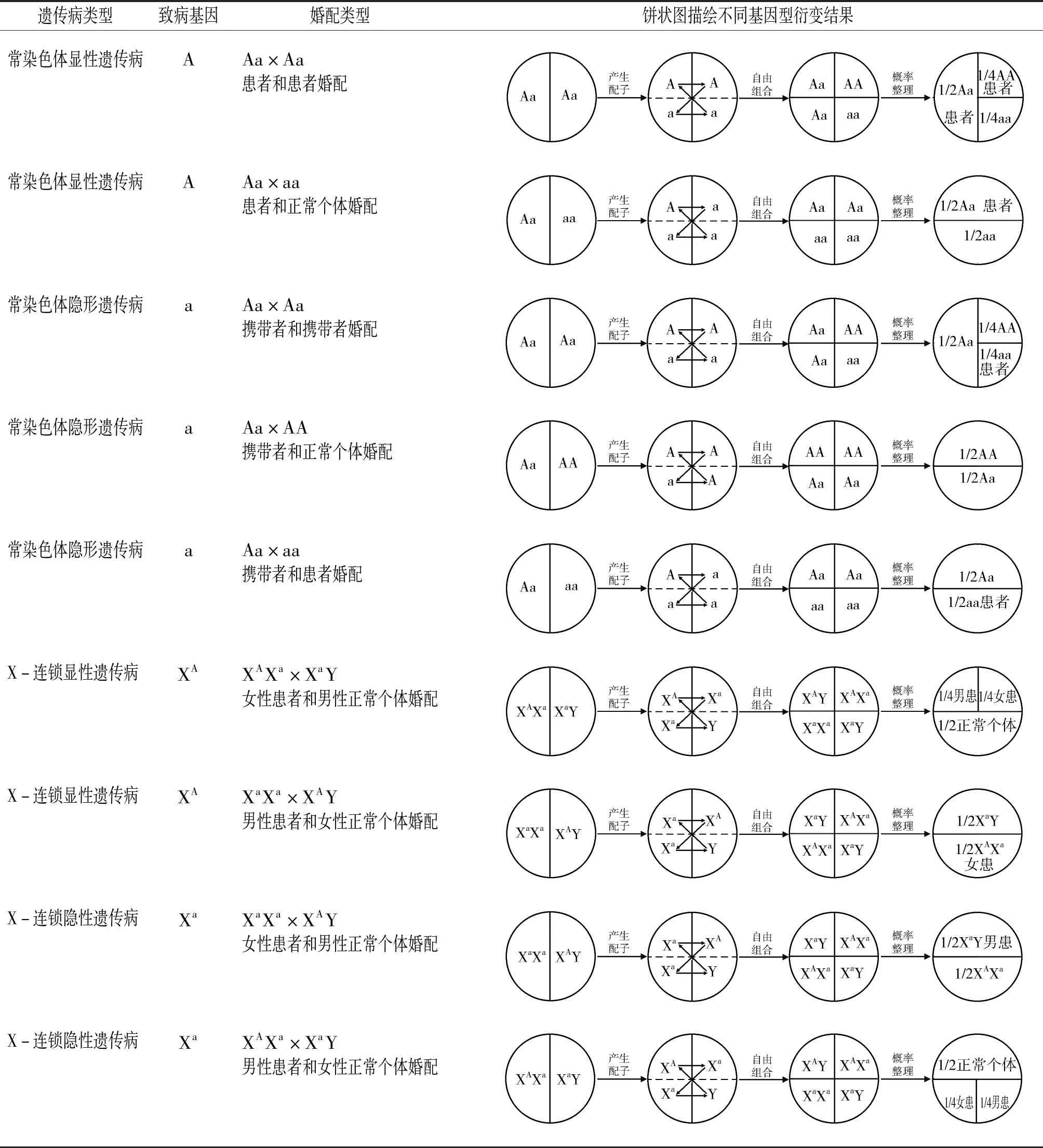
表1 饼状图描绘不同单基因遗传病后代个体基因型产生的过程

2.2 集合图比较质量性状与数量性状的遗传特点

质量性状是指单基因遗传的性状，代表在一个大的群体中，由各个表型组成的小群体之间是独立的，彼此有“质”的区别；数量性状是指多基因遗传的性状，代表在一个大的群体中，个体之间是连续的变化，只有“量”的增减[5]。此概念在教材中以正态分布图形展示，偏于抽象。故我们在教学中补充了集合图形加以说明，以一个集合代表一个群体的“直映”方式帮助学生更好地理解质量性状与数量性状的不同特征及应用，如图1、图2所示。

图1 集合图像描绘质量性状遗传特征

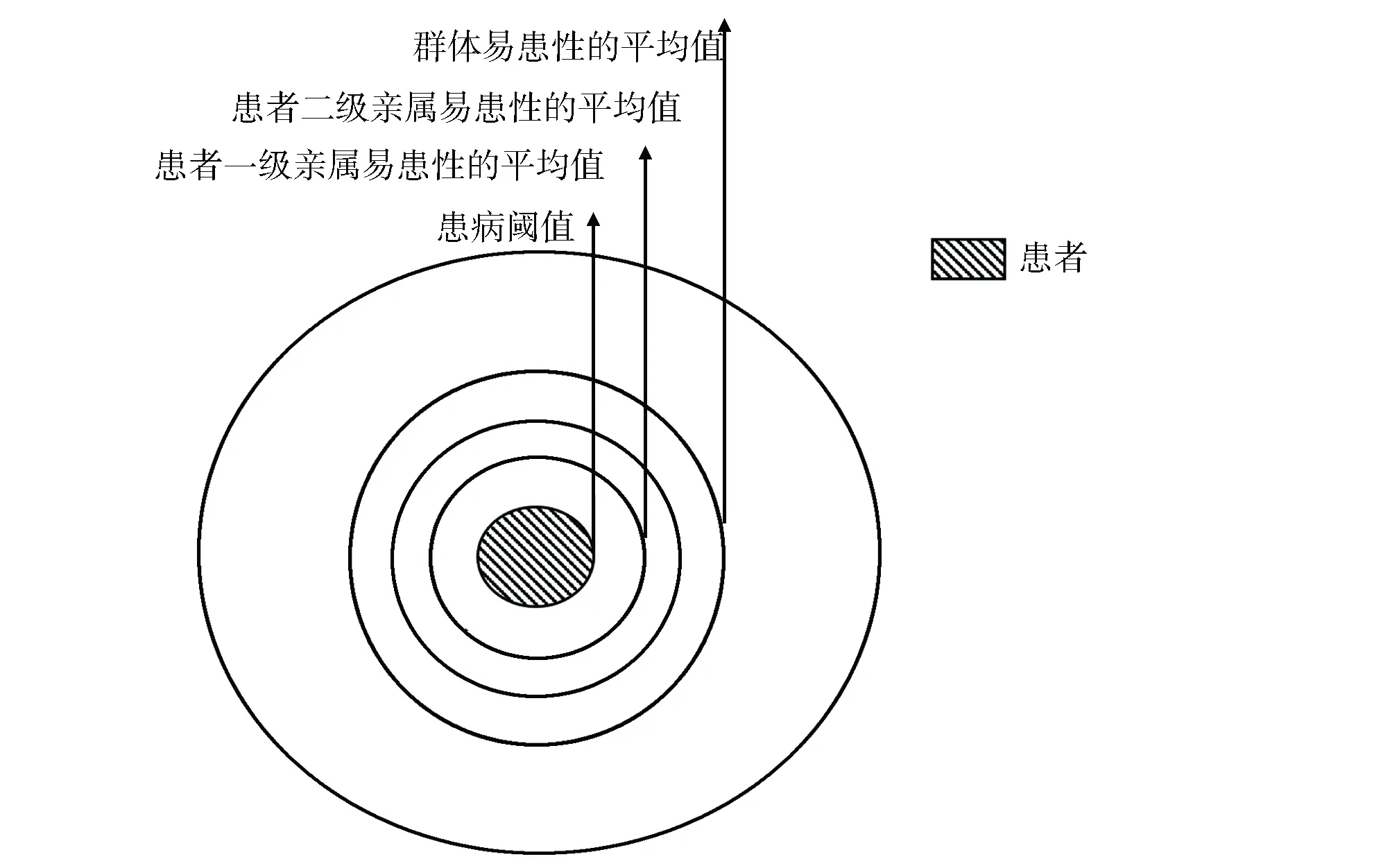
图2 集合图像描绘数量性状遗传特征及亲属发病风险

如图1所示，以一个封闭曲线围绕的集合代表一个群体，各个空间由不同的图案填充，说明彼此之间有质的区别，这是质量性状的典型特征：可以将具有共同特征的个体归为一个集合中，相互不连续；图2则描绘了数量性状的遗传规律，在一个大的群体中，除患者之外，其余个体之间没有质的区别(图中均以空白填充表示)，是连续的。另一方面，通过若干个同心圆的切线表示易患性的平均值，从图中容易看出，由患病阈值向外延伸，顺梯度方向，群体易患性降低。根据这个规律，学生可直观比较患者一级亲属和二级亲属的易患性。集合图像的应用将课程数学问题简单化，便于学生理解。

2.3 坐标曲线图描绘遗传平衡群体各基因型的分布规律

遗传平衡定律是群体遗传学的基本原理，指在没有迁移、突变和选择等因素下，一个大的连续随机交配群体的基因频率和基因型频率世代相传都不会发生变化，并且群体的基因频率和基因型频率之间符合二项式分布的简单关系[6]，对计算平衡群体中某个疾病的群体患病率、致病基因频率有重要的意义。因此，教师首先建立了基因频率与基因型频率的函数关系，然后借助数学坐标曲线图形象描绘遗传平衡群体的特征，具体见表2。

研究将函数自变量固定为A的基因频率，让学生直观感受随着一种基因频率的变化，整个群体中不同基因型的占比概率。更重要的是，经过坐标曲线的绘制，我们发现只有当A和a的基因频率相同均为0.5时，Aa的基因型频率可以取到最大值0.5。这一结论可以帮助学生直接判断某个已知群体是否为平衡群体，并且可以使其意识到杂合子的基因型频率呈现先升高后降低的趋势，而这对于维持整个群体的平衡是非常重要的。数学坐标曲线图的应用，深入了课程知识的理解，也为学生解题提供新的思路。教学过程中，教师将上图用于分析单基因常染色体遗传病的概念，以A或a为致病基因，请学生分析一个群体中患者或携带者的频率变化，或通过类似的方式绘制X-连锁遗传病中各基因型的曲线变化图，帮助学生更好地应用遗传平衡定律。

3 讨论

医学遗传学部分引入数学图像的教学模式得到了学生的认同。在后期的调查问卷中，显示有98%以上的学生会应用这些图像分析问题，并且对于教材中出现的数学内容有深入理解。在2019级中医学专业期末考核过程中，医学遗传学的知识内容占比55%，其中涉及数学理解的部分有28分，成绩统计显示学生的答题正确率达84.35%，较2018级学生平均提高5个百分点，见表3。

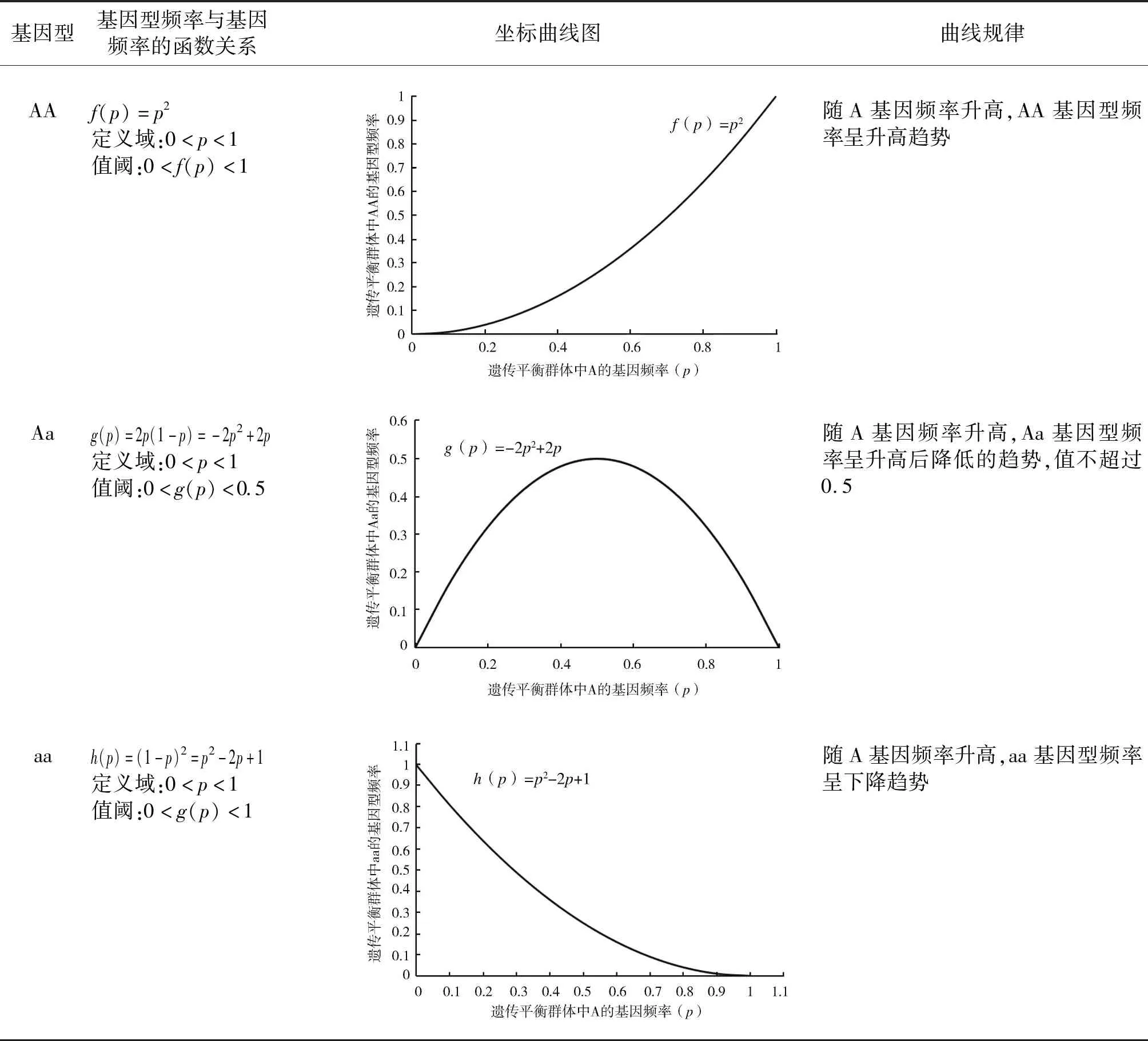
表2 坐标曲线图描绘遗传平衡群体基因频率与基因型频率的函数关系

表3 坐标曲线图描绘遗传平衡群体基因频率与基因型频率的函数关系 (%)

据此，研究显示虽然数学本身具有严谨精确、逻辑性强等特点，但数学思维的应用并不会将课程问题变得复杂深奥。相反，正确使用数学方法可使遗传学内容更为简单形象的体现。将数学引入课程，提倡跨学科教育，也是近十年来我国很多学者探讨的STEAM教育模式，其中S指科学(science)、T指技术(technology)、E指工程(engineering)、A指艺术(art)、M指数学(mathematics)[7]。在医学遗传学教学内容中引入数学图像后，由于师生讨论频率增加，课堂活跃度明显提高，学生学习氛围浓厚；同时在解题过程中，由于数学思维方法的建立，学生认为有章可循、有法可依，极大提高了解题正确率。

马克思说过，“一种科学只有成功运用数学思想，才能达到完善[8，9]。”伽利略认为：“自然的语言就是数学，要表达自然的运动规律，应该使用数学和实验数据[10]。”而医学生需要具有思维严密、善于思考的能力，同时具备重事实、重实践的端正的科学态度，这些品格都可以通过数学的学习而得到培养。因此，我们需要不断坚持将更成熟的数学思想和更多的数学方法引入教学过程，努力的方向主要有以下两点：课程组教师的数学逻辑水平需要持续提高；要从传统的培养学生的形象思维能力转变至提升其类比、迁移及推理的能力，以保证在共同的努力下，可实现优化教学、提升教师与学生对问题的理解层次，培养多思路、多角度解决问题的能力。