点接触曲线构型内啮合齿轮传动接触特性分析

梁栋， 孟胜

(重庆交通大学机电与车辆工程学院， 重庆 400074)

内啮合齿轮副被广泛应用在机械传动系统中，因为其具有结构紧凑、传动效率高、噪声小等特点，常用于航空航天、风力发电、电动汽车等领域[1]。近年来，中外学者对内啮合齿轮传动开展了一系列研究工作。

何迪等[2]提出了一种平行轴纯滚动内啮合线齿轮的设计方法，推导出齿面方程，构建了三种不同接触形式的齿面，通过运动学仿真验证了齿轮传动的平稳性和连续性。王延忠等[3]和Wang等[4]提出了一种基于圆弧啮合线的大重合度内啮合齿轮构造方法，以圆弧为啮合线来构建齿廓，分析了齿轮的重合度、滑动率、相对法曲率等特性，较渐开线齿轮而言，其传动性能有着很大的提升。唐沛等[5-6]提出了一种具有大重合度特性的新型齿廓齿轮，建立了新型齿轮齿廓，推导了齿轮接触应力表达式，并进行有限元分析，结果验证新型齿轮具有重合度大、滑动率小、承载能力强等优点。Peng等[7-8]提出了一种基于空间啮合理论的点接触内啮合斜齿轮副，它由渐开线内齿轮和具有二次曲线齿廓的小齿轮组成。尤其是齿面的接触路径是可选择的，可以继承齿面的特性。而且，这种类型的内齿轮对装配误差的敏感性较低，拥有较小的滑动率。段振云等[9]针对中小模数内齿轮结构所限，齿面淬硬后的齿形加工难以使用传统磨齿工艺等问题，提出了一种电火花成型铣削加工方法，设计了加工装置并完成相关实验分析，结果表明新加工方法得到的工件表面质量与加工效率有显著提高。张国政等[10]提出了采用内啮合齿轮副传动模拟代替内齿珩轮强力珩齿运动。根据Hertz接触原理，引入压比系数计算不同啮合点位置的应力，分析验证外圆柱斜齿轮齿面不同位置的应力分布情况，进而说明内齿珩轮强力珩齿时被珩工件齿轮的齿面应力分布。Sánchez等[11-12]针对渐开线内啮合齿轮副啮合受载不均问题，基于Hertz接触理论提出了内啮合齿轮接触应力与弯曲应力的修正计算公式，并用有限元分析方法验证了公式的准确性。李智等[13]利用Hertz接触理论和粗糙表面形貌的Greenwood-Williamson理论，建立了粗糙齿面单微凸体法向正接触模型、粗糙齿面弹塑性接触模型和不同粗糙度的粗糙界面接触有限元模型等，分析了微凸体对齿面接触特性及疲劳寿命影响分析。王靖岳等[14]考虑摩擦、时变啮合刚度、齿隙和综合误差等非线性因素，建立了行星齿轮系统扭转振动模型，结合非线性分析方法分析了系统的分岔行为和齿面摩擦对系统分岔特性的影响。

因此，现基于齿轮空间啮合理论，建立一种点接触曲线构型内啮合齿轮传动基本模型，提出齿面成型原理与一般方法；进一步对该成型内啮合齿轮副的接触特性，如运动特点、重合度、滑动率、诱导法曲率和曲率干涉等问题进行探讨和分析，揭示齿面接触特点和啮合规律，为后续构建高性能齿轮传动副奠定理论基础和技术支撑，相关研究具有重要的理论意义和工程应用价值。

1 点接触曲线构型内啮合齿轮传动基本数学模型

在前期研究中以空间曲线为几何元素，建立了适用于外啮合齿轮传动的共轭曲线基本理论[15-16]。在此基础上，进一步提出了点接触曲线构型内啮合齿轮传动形式，其主要过程如图1所示，图1中P点为曲线1和曲线2的公共接触点。

图1 点接触曲线构型内啮合齿轮传动成型原理与方法Fig.1 Generation principle and method of point-contact internal gear drive with curve construction

图1中步骤(1)过程中，通过建立空间共轭曲线副基本啮合坐标系，分析空间曲线接触状态下相对运动速度关系和法矢量位置关系，构建沿指定公法线方向的空间曲线啮合函数，进而得到一对空间共轭啮合曲线副——曲线1和曲线2，曲线1和曲线2的一般方程为

(1)

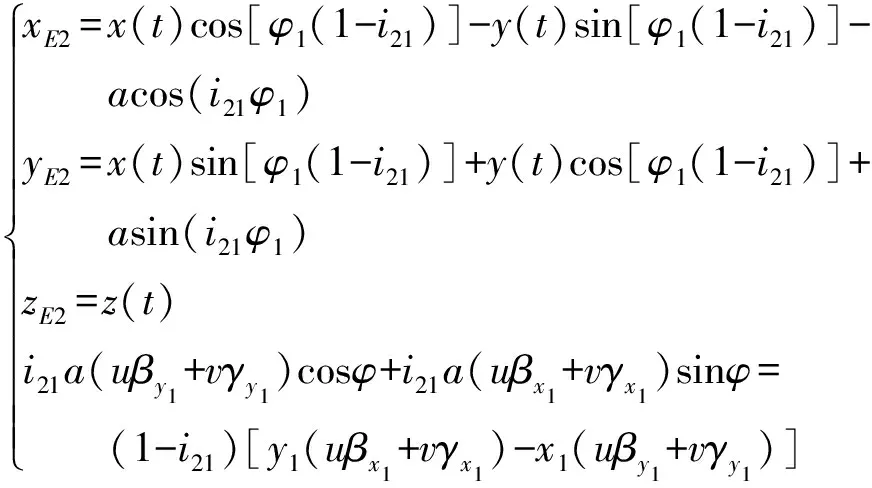
(2)

式中：xE1、yE1、zE1为曲线1在啮合坐标系中沿各坐标轴x、y、z方向的表达式；xE2、yE2、zE2为曲线2在啮合坐标系中沿各坐标轴x、y、z方向的表达式；t为空间曲线参数；i21为内齿轮啮合副传动比；φ1为小齿轮1的旋转角度；a为齿轮啮合副的中心距；βx1、βy1为在曲线接触点处主法矢方向的分量；γx1、γy1为在曲线接触点处副法矢方向的分量；u、v为接触角位置分量。

分别以该空间共轭啮合曲线副为齿面接触轨迹线，采用等距包络方法得到一对啮合的包络曲面，而空间共轭曲线副也分别是各自成型曲面上的唯一接触迹线，曲面方程分别为

(4)

图1中步骤(2)过程中，进一步将得到的包络曲面通过齿顶、齿根区域设定等形成理想齿廓。对比分析过程中发现，改变两成型曲面的相对位置及半径，可以不同的接触方式。当空间共轭曲线1和2等距方向相同，等距距离l1和l2取值满足l2=(1.1～1.2)l1时，可构造出具有理想接触特征的凸-凹齿廓形式。对于点接触曲线构型内啮合齿轮传动来说，可实现少齿数、大模数特性设计。

2 齿面接触特性分析

2.1 运动特性

基于MATLAB软件建立如图2所示点接触曲线构型内啮合齿轮副运动模型。假定齿轮以恒定的角速度转动，图2(a)为该内啮合齿轮副初始啮合的位置，空间原始曲线与共轭曲线沿轴向啮合线呈点接触；图2(b)～图2(d)分别为该内啮合齿轮副旋转20°、40°和60°时的接触状态。可以看到，啮合线是沿着齿宽方向分布的一条直线，随着该内啮合齿轮副的旋转运动，接触点沿啮合线轴向移动。

图2 点接触曲线构型内啮合齿轮副运动模型Fig.2 Motion model of point-contact internal gear drive with curve construction

2.2 重合度

合理的重合度有利于提高齿轮传动的平稳性和提高承载能力。如图3所示，B1B1段和B2B2段分别表示在啮合平面内，同一对轮齿从开始啮合到退出啮合时的位置。B1B1段和B2B2段直线之间区域是齿轮的啮合区。

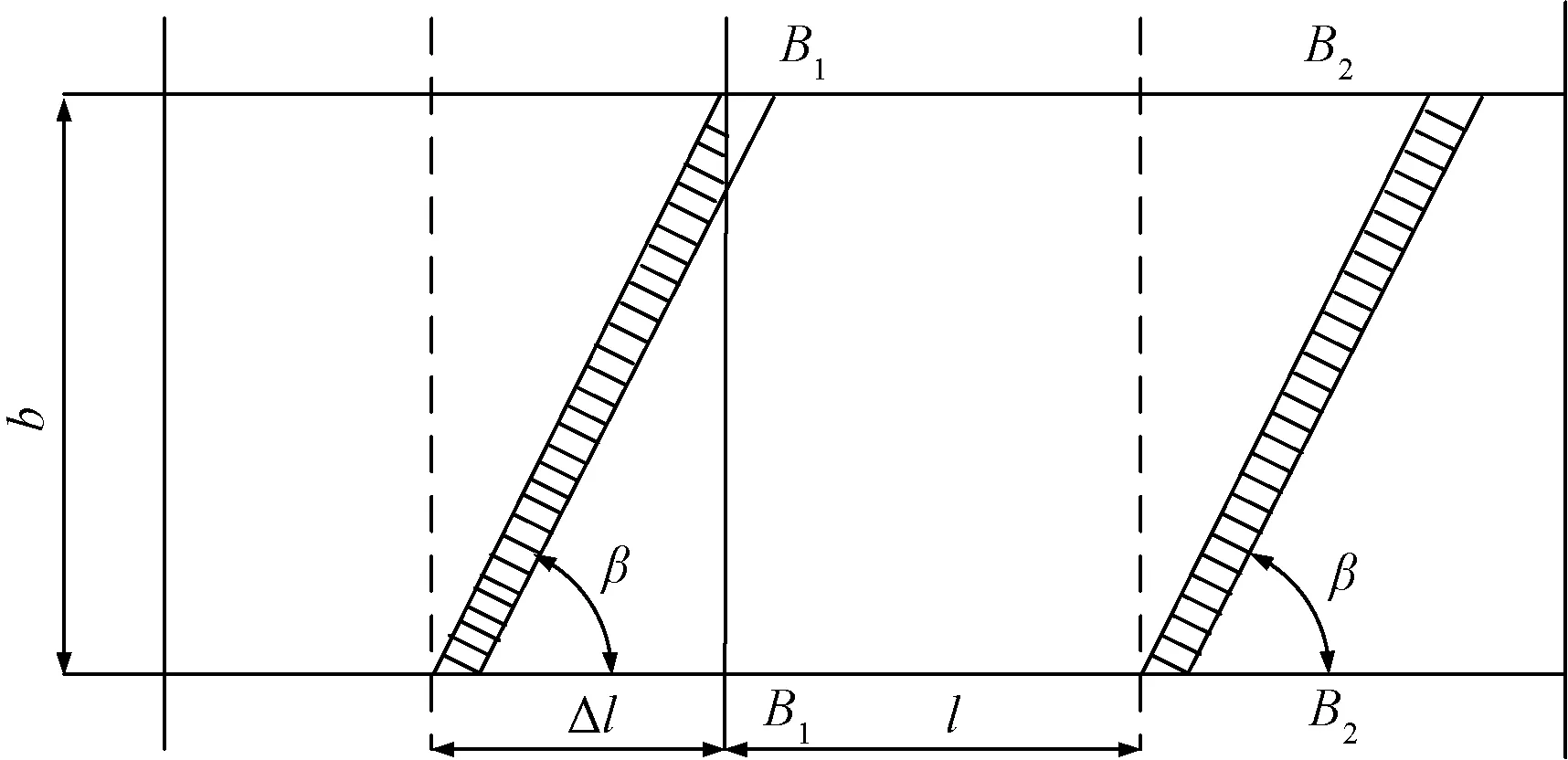
图3 重合度分析Fig.3 Coincidence analysis

对于点接触曲线构型内啮合斜齿轮副来说，由于不是沿整个齿宽同时进入啮合，而是先从轮齿一端进入啮合，随着齿轮旋转运动而逐渐地沿整个齿宽接触。退出啮合时也是由轮齿一端先行退出啮合，直到该轮齿转到图中虚线位置时，整个轮齿才全部退出啮合。因此，相较于内啮合直齿轮副来说，该齿轮副啮合区要大Δl的距离。

特别地，由于该齿轮副的接触运动形式为沿轴向点接触形态，故其端面重合度为零，仅有轴向重合度，重合度εβ的计算公式为

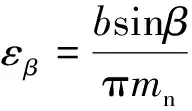
(5)

式(5)中：b为齿宽；mn为齿轮法面模数；β为齿面螺旋角。

2.3 滑动率

2.3.1 计算方法

滑动率是一对啮合齿轮间的磨损和润滑的评判准则，较低的滑动率的齿轮副有着更好的润滑条件以及更低的摩擦，从而使得其传动性能更好[17]。

(7)

图4 滑动率分析Fig.4 Sliding ratio analysis

进一步，以空间圆柱螺旋线为例，对该内啮合齿轮副进行计算分析，假定小齿轮1上的空间圆柱螺旋线方程为

(8)

式(8)中：x1、y1、z1为空间圆柱螺旋线1在啮合坐标系中沿各坐标轴方向的表达式；r为基圆圆柱半径；θ为圆柱螺旋线参数；p为螺旋参数。

根据式(1)和式(2)中计算结论，内齿轮2上与之共轭的曲线方程为

(9)

将式(8)和式(9)分别代入式(6)和式(7)中计算可得

(11)

将表1中的齿轮副设计参数代入式(10)和式(11)中计算，可得如图5所示的齿面滑动率结果。

由图5可知，该点接触曲线构型内啮合齿轮副的齿面滑动率结果为常数且接近于零，其不随曲线参数θ改变而发生变化，由此该啮合副接触过程为近似纯滚动状态，无较大摩擦磨损发生，易提高传动效率。

表1 内啮合齿轮副设计参数

图5 滑动率计算结果Fig.5 Calculation results of sliding ratios

2.3.2 滑动率影响因素分析

(1)模数。为了研究模数对该齿轮副齿面滑动率的影响，设置了三组对比参数，分别将模数设置为2、4和6，其余参数保持一致即传动比i=0.2，螺旋参数p=120/2π。借助MATLAB软件编写计算程序，得到如图6所示结果。可见，该齿轮副的齿面滑动率结果会随着设计模数的增加而逐渐减小。

(2)传动比。探讨传动比对齿轮副滑动率的影响，仍设置三组对比参数，将传动比分别设置为6/30、6/45和6/60，其余参数保持一致即模数m=6，螺旋参数p=120/2π。通过计算分析得到如图7所示结果，该齿轮副的齿面滑动率结果随着传动比的减小而逐渐减小。

(3) 螺旋参数。参照前面的做法，研究螺旋参数对齿轮副滑动率的影响，设置三组对比参数，将螺旋参数分别设置为120/2π、150/2π和180/2π，其余参数保持一致即模数m=6，传动比i=0.2。通过计算分析得到如图8所示结果，该齿轮副的齿面滑动率结果随着螺旋参数的增大而逐渐减小。

图6 模数影响Fig.6 Influence of modulus

图7 传动比影响Fig.7 Influence of transmission ratio

图8 螺旋参数影响Fig.8 Influence of spiral parameters

对滑动率影响因素的分析可以对后续的齿轮设计提供参考，选择合理的设计参数提高齿轮的传动效率。

2.4 齿面法曲率分析

根据微分几何理论，结合式(3)和式(4)结果，将该内啮合齿轮副齿面方程列为r=r(t,φi)，其中i=1,2，其单位法矢量n进一步表示为

(12)

由于dn=ntdt+nφidφi，dr=rtdt+rφidφi，那么法曲率Kn为

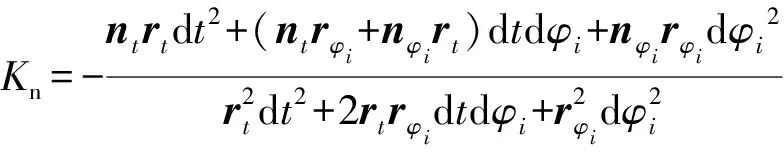
(13)

而nrt=0,nrφi=0。分别对t、φi取偏导数，即

(14)

所以有

ntrφi=nφirt

(15)

因此齿面法曲率Kn又可以表示为

(16)

2.5 齿面干涉分析

点接触曲线构型内啮合齿轮齿面的啮合实质是齿面上一对空间共轭曲线的点接触啮合运动，该配对空间共轭曲线的选取是根据设计需求，在一定取值范围内的特定曲线。

当配对的内啮合齿轮副在某一点处接触时，如果小齿轮和内齿轮的齿面曲率半径差太小，或者某一齿轮齿顶伸入到过渡曲线内，或由于制造装配等原因会导致在接触点处存在啮合干涉。

图9 齿面啮合干涉Fig.9 Meshing interference of tooth surfaces

如图9所示，当一对成型齿面在K点处正常啮合时，凸、凹圆弧齿廓在该点处呈点接触且满足一定条件的曲率及啮合关系。当存在啮合干涉时，齿面不是处于正常点接触状态，而是一个齿面嵌入另一个齿面，导致成型齿廓之间相交于M1、M2点。图9中K′为齿面实际嵌入点，KK′为理论接触点和实际嵌入点之间的最大距离，用Δk表示，则齿面啮合干涉量为

(17)

3 结论

(1) 提出了点接触曲线构型内啮合齿轮传动形式，依据空间共轭曲线副建立了点接触曲线构型内啮合齿轮传动的基本数学模型，构建了具有理想接触特点的齿廓接触类型，给出了该内啮合齿轮副的齿面方程。

(2)开展了点接触曲线构型内啮合齿轮传动接触特性分析，基于MATLAB软件建立了该内啮合齿轮副运动模型，讨论了齿轮不同旋转运动角度下齿面实际接触状态即配对齿面在轴向上沿空间共轭曲线副点接触运动。

(3)提出了该内啮合齿轮副齿面重合度计算分析方法，依据齿面接触实质建立了齿面滑动率计算方法，进一步以空间圆柱螺旋线为例验证相关结论，结果表明：该啮合副接触过程为近似纯滚动状态，无较大摩擦磨损发生，易提高传动效率；分别以模数、传动比和螺旋参数为变量，分析了不同参数对齿面滑动率影响变化规律。

(4)提出了该内啮合齿轮副齿面法曲率一般计算公式和齿面干涉分析依据等。后续将进一步对点接触曲线构型内啮合齿轮传动齿面接触力学特性开展研究。