增强同步挤压Stockwell变换和改进集成深层极限学习机的轴承工况识别方法
2022-12-04杜小磊肖龙周庆辉陈志刚
杜小磊, 肖龙, 周庆辉, 陈志刚
(1.电子科技大学 机械与电气工程学院,四川 成都 611731; 2.北京理工大学 前沿技术研究院,山东 济南 250300; 3.北京建筑大学 机电与车辆工程学院,北京 100044)
0 引 言
电机被广泛应用于数控机床和航空航天等领域,而电机滚动轴承是电机的重要部件,对电机轴承工况状态进行监测与识别具有重要意义[1]。
传统基于“特征提取—特征选择—模式识别”的轴承工况识别方法[2]已得到广泛应用,但轴承振动信号由于多个振源的激励与响应相互耦合,非线性和非平稳性较为强烈[3],从振动信号中选择敏感特征较难;而且在大数据时代,浅层分类器面临维数灾难问题[4]。深度学习[5]能自动从振动信号中进行特征学习,一定程度上摆脱了对繁琐的特征提取和选择技术的依赖。目前基于“振动信号时频谱图—深度学习”的轴承工况识别方法研究较多,Verstraete等[6]将3种时频谱输入深层卷积网络,以较少的学习参数获得了较好的识别结果;Ma等[7]将轴承振动信号的小波时频谱图输入深度信念网络实现了对轴承工况的有效识别;Xu等[8]将电机轴承振动信号的Stockwell变换时频谱图输入深度降噪自动编码器进行工况识别,识别准确率达96%。上述研究均利用“时频谱图—深度学习”模型实现了电机轴承工况识别,但小波变换和Stockwell变换等时频谱图的时频分辨率较低,时频谱聚集性较差,难以给深度学习模型提供优秀的训练样本[9],同步挤压Stockwell变换(synchrosqueezed stockwell transform,SST)[10]改进了Stockwell变换的时频能量发散状况,但抗噪能力较差;且单一的深度学习模型存在泛化能力低的缺陷[11]。
在前述研究的基础上,本文提出一种基于增强同步挤压Stockwell变换(enhanced synchrosqueezing stockwell transform,ESST)结合改进集成深层极限学习机(improved ensemble deep extreme learning machine,IEDELM)的电机轴承工况识别方法。所提ESST方法有效改善传统时频分析时频谱聚集性差和抗噪能力差的缺陷,为深度学习模型提供了优秀的训练样本;而IEDELM在深层极限学习机的基础上引入自组织策略、卷积策略和集成学习策略,有效提高模型的鲁棒性,并通过实验验证ESST-IEDELM方法的可行性和有效性。
1 增强同步挤压Stockwell变换
1.1 理论基础
为克服SST抗噪能力差的缺陷,本文提出一种更精确、抗噪能力更强的瞬时频率估计ESST方法。ESST首先利用谱重排算子计算局部瞬时调制算子,然后在频率方向进行同步挤压变换,进而修正瞬时频率。定义信号x(t)的Stockwell变换为
(1)
式中:τ为时间;f为频率。SST对Stockwell变换的瞬时频率进行精确估计,瞬时频率计算为
(2)
式中R{}取实数算子。由此可得
(3)
SST通过将Stockwell变换频率方向的模糊能量“挤压”到瞬时频率脊线附近,有效提高了时频分辨率。但SST只在频率方向进行重分配,存在时域能量溢出和抗噪能力差的缺陷,因此本文提出ESST。
首先,定义高阶局部调制系数
(4)
其中:
(5)
(6)
高阶瞬时频率估计计算为
(7)
因此,x(t)的ESST变换计算为
(8)
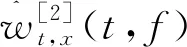
1.2 仿真分析
采用下面的仿真信号进行分析:
(9)
其中:f1(t)为余弦信号;f2(t)、f3(t)为调频信号;f4(t)为调幅-调频信号;f5(t)为高斯白噪声。
分别采用小波变换、Stockwell变换、SST和ESST对f(t)进行时频分析,时频谱分别如图1~图4所示。
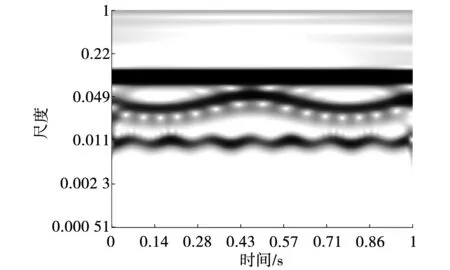
图1 仿真信号的小波变换时频谱图
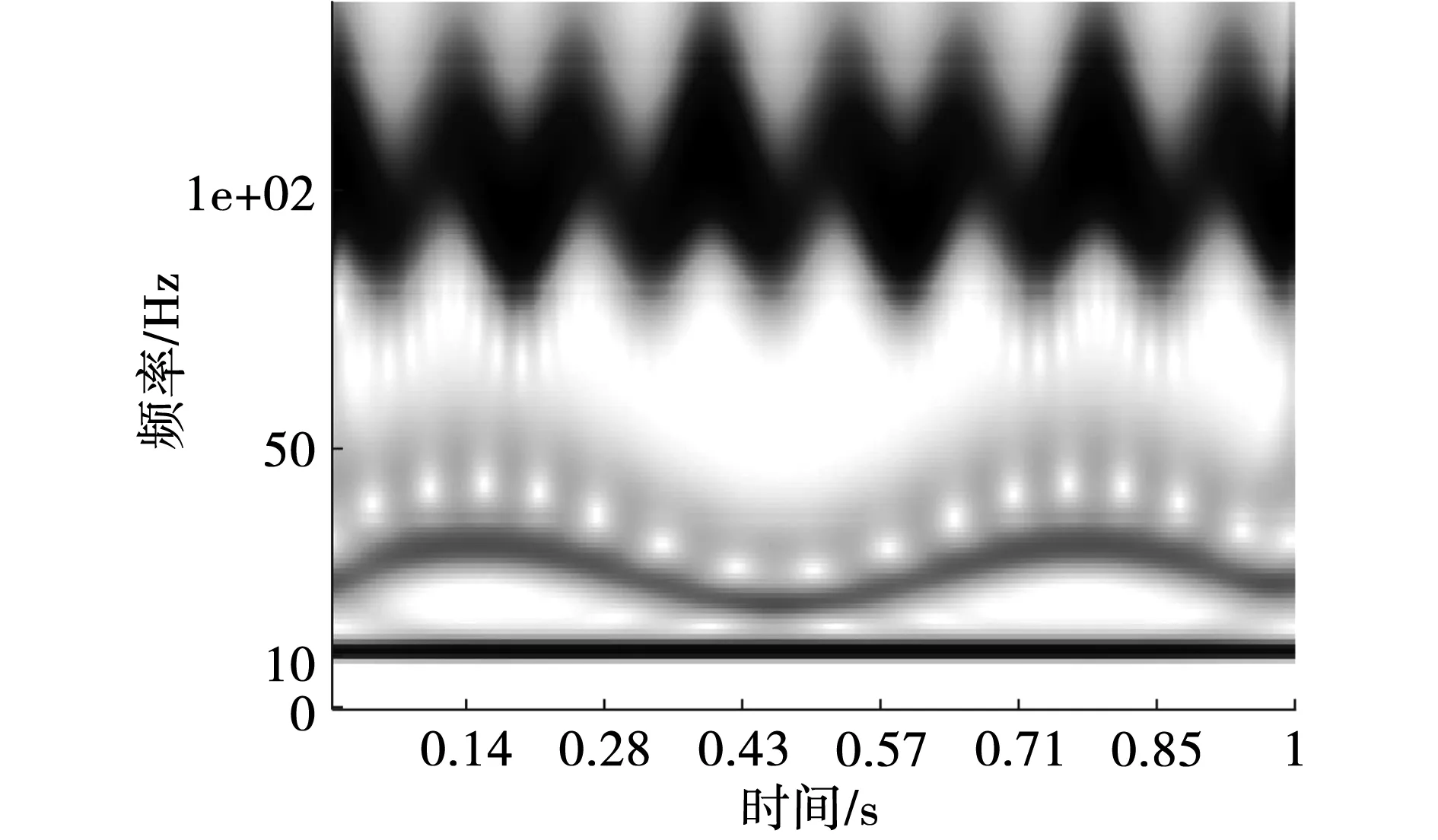
图2 仿真信号的Stockwell变换时频谱图
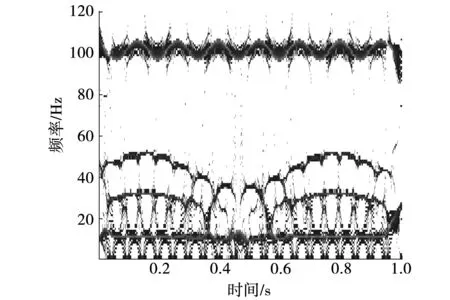
图3 仿真信号的SST时频谱图
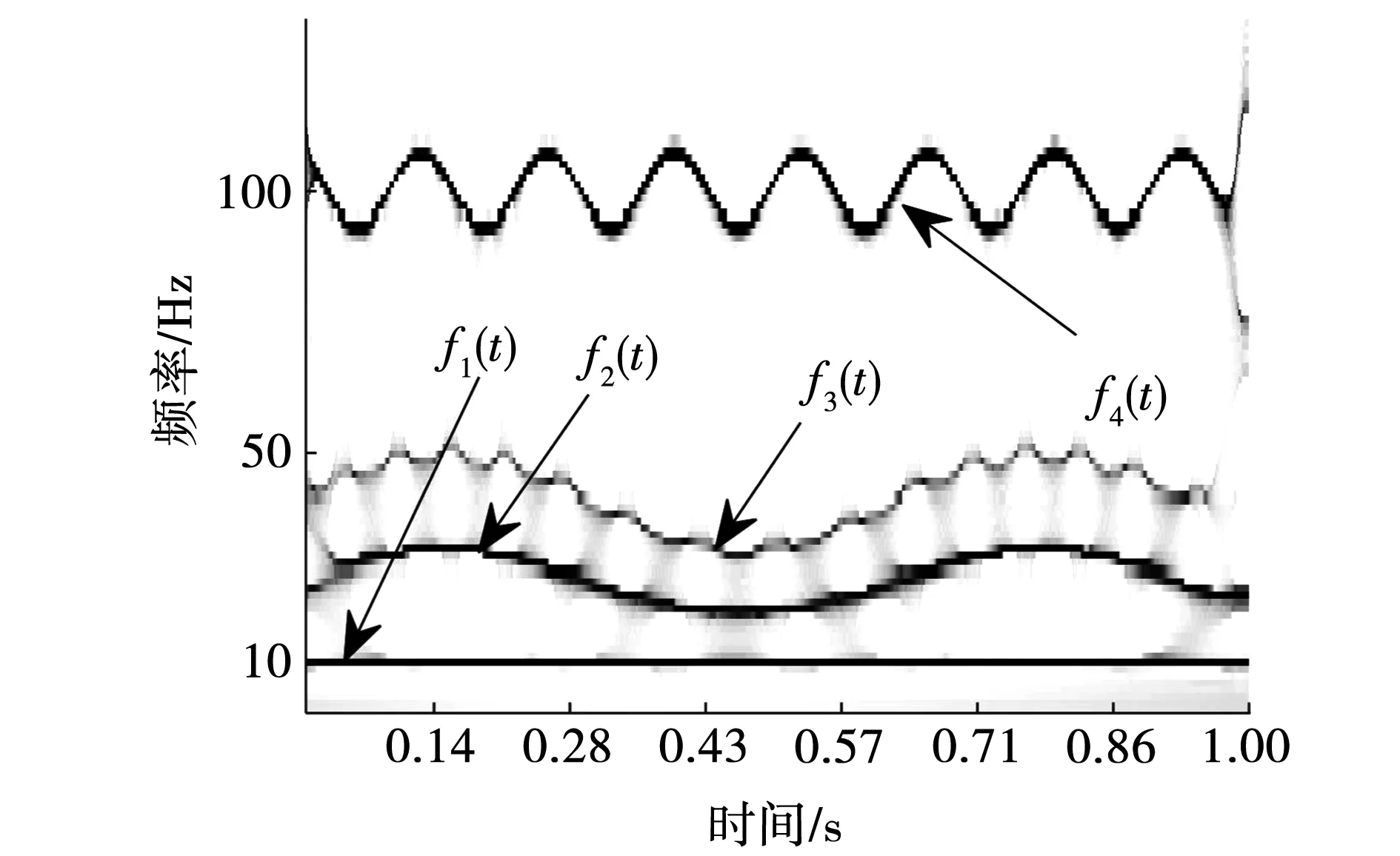
图4 仿真信号的ESST时频谱图
由图可以看出:小波变换和Stockwell变换时频分辨率较低;SST时频谱瞬时频率变化趋势较清晰,但受噪声干扰严重,仍存在一定程度的模糊现象;ESST时频谱更有效地捕捉了信号的频率变化信息,抗噪能力更强,时频谱聚集性和时频分辨率更高。
2 改进集成深层极限学习机
2.1 深层极限学习机
深层极限学习机(deep extreme learning machine,DELM)[12]将深层自动编码器与极限学习机结合,兼具深度学习方法自动特征提取和极限学习机训练速度快的优势。
设DELM输入层神经元个数为m,第1隐层的神经元个数为L,第一步是将输入x通过sigmoid函数转换为隐层特征h=[h1,h2,…,hL]T,有
h=sigmoid(Wx+b)。
(10)
式中:W为输入层到第1隐层之间的权值向量;b为偏置向量,第1隐层的输出为
y=hTβ。
(11)
式中β为隐层到输出层的权重向量。
第一层损失函数表示如下:
(12)
式中β为第1隐层的输出权重,计算如下:
(13)
式中:H为隐层映射矩阵;I为单位矩阵。DELM的详细训练步骤见文献[12]。
2.2 改进深层极限学习机
DELM为全连接网络,受噪声影响较大;卷积神经网络(convolutional neural network,CNN)具有稀疏连接与权值共享特性,可减少网络间的连接,抗噪能力较强。因此本文将DELM与CNN结合,构造改进深层极限学习机(improved deep extreme learning machine,IDELM),IDELM的基本单元如图5所示。
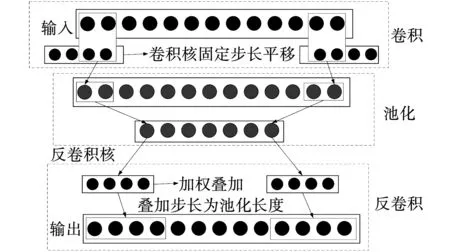
图5 IDELM基本单元结构
设IDELM基本单元输入为x,以高斯小波激活函数为例,隐层第k个神经元输出如下:
hk=ψ[(x*Wk-ck)./ak];
(14)
(15)
式中:ψ为高斯小波函数;Wk为卷积核权重;ak为尺度向量;ck为平移向量;*为卷积符号;./为按元素相除符号。则基本单元结构输出如下:
(16)
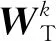
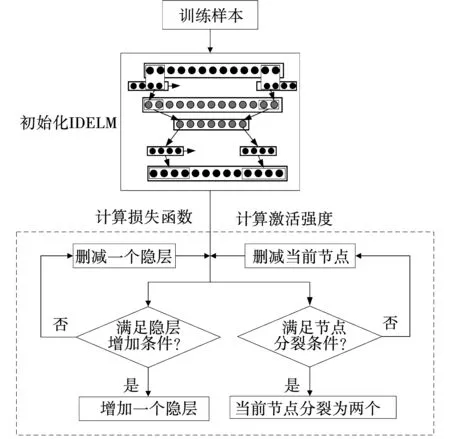
图6 自组织策略
在网络训练阶段将隐层节点激活强度作为节点的“贡献度”,并根据“贡献度”大小对节点进行增加或删减;并将损失函数的梯度下降率作为隐层的删减标准,当损失函数梯度下降率首次出现递减时删掉一个隐层,否则增加一个隐层,激活强度为
(17)
式中:α>0为常数;oi.l为第l个隐层的第i个节点的输出,Nl为第l个隐层节点个数;si.l为第l个隐层的第i个节点的输入权值之和,计算如下:
(18)
式中:rij为第i个节点的第j个输入;wij为第j个节点和第i个节点的连接权重。
2.3 集成学习方法
单一的IDELM泛化能力较差,IEDELM通过集成多个IDELM可获得比单一IDELM更好的工况识别结果。本文利用 9个具有不同激活函数的IDELM完成电机轴承工况识别,9种激活函数的方程列于表1。

表1 不同激活函数的方程
当第i个IDELM的识别结果为outi时,IEDELM的集成学习结果Y计算如下:
(19)
(20)
式中pi为9个IDELM的识别精度排序序号,pi由F1确定,F1的计算公式为
(21)
其中:
(22)
(23)
式中:TP为正样本中被模型判断为正的个数;FP为在负样本中被模型判断为正的个数;FN为正样本中被模型判断为负的个数,F1在[0,1]之间,反映查准率和召回率的信息,0代表最差,1代表最好。综上,ESST-IEDELM算法流程如图7所示,步骤如下:
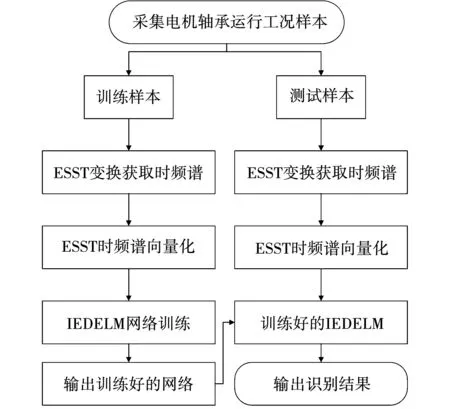
图7 工况识别流程图
1)采集不同工况的电机轴承振动信号样本,随机选取80%作为训练样本,剩余作为测试样本;
2)对训练样本和测试样本进行ESST变换得到时频谱图并进行向量化操作;
3)将ESST时频列向量训练样本输入IEDELM进行训练,训练完成后使用测试样本对训练好的模型进行测试。
3 实验验证
3.1 实验数据
为验证ESST-IEDELM方法的有效性,以电机轴承试验台为对象,如图8所示。

图8 电机轴承测试实验台
实验台由电机、测试电机轴承、转速控制器、转轴等组成,可调节工况包括转速与径向力,测试电机轴承参数如表2所示,工况设置如表3所示。采用加速度传感器和信号采集器采集电机轴承振动数据,采样频率20 kHz。
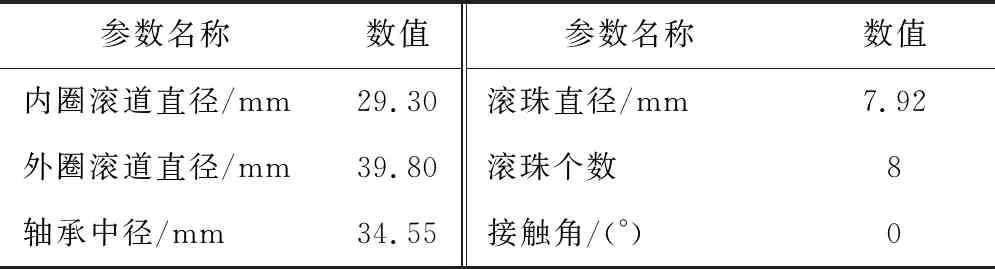
表2 测试轴承参数

表3 工况设置
使用电火花技术在电机轴承内圈、外圈和滚动体上加工尺寸为 0.15、0.32 mm的环槽损伤以模拟轻微故障和中度故障。参考文献[14]的工况设置方法,选取8种工况进行研究,如表4所示。每种工况8 000个样本,每个样本1 024个采样点,图9为轴承运行工况时域图。
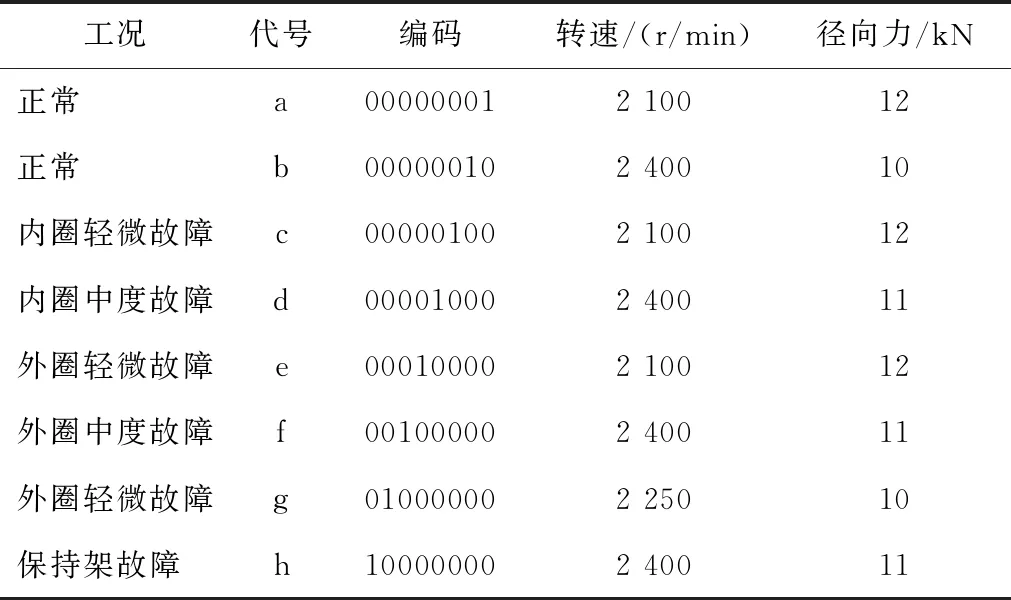
表4 8种轴承运行工况
由图9可知,故障工况a~h的振动信号的故障冲击信息被环境噪声淹没,故障脉冲特征极其微弱,因此难以直接在时域波形图中对滚动轴承的运行工况进行有效区分,有必要进一步对各工况振动信号进行时-频谱分析。
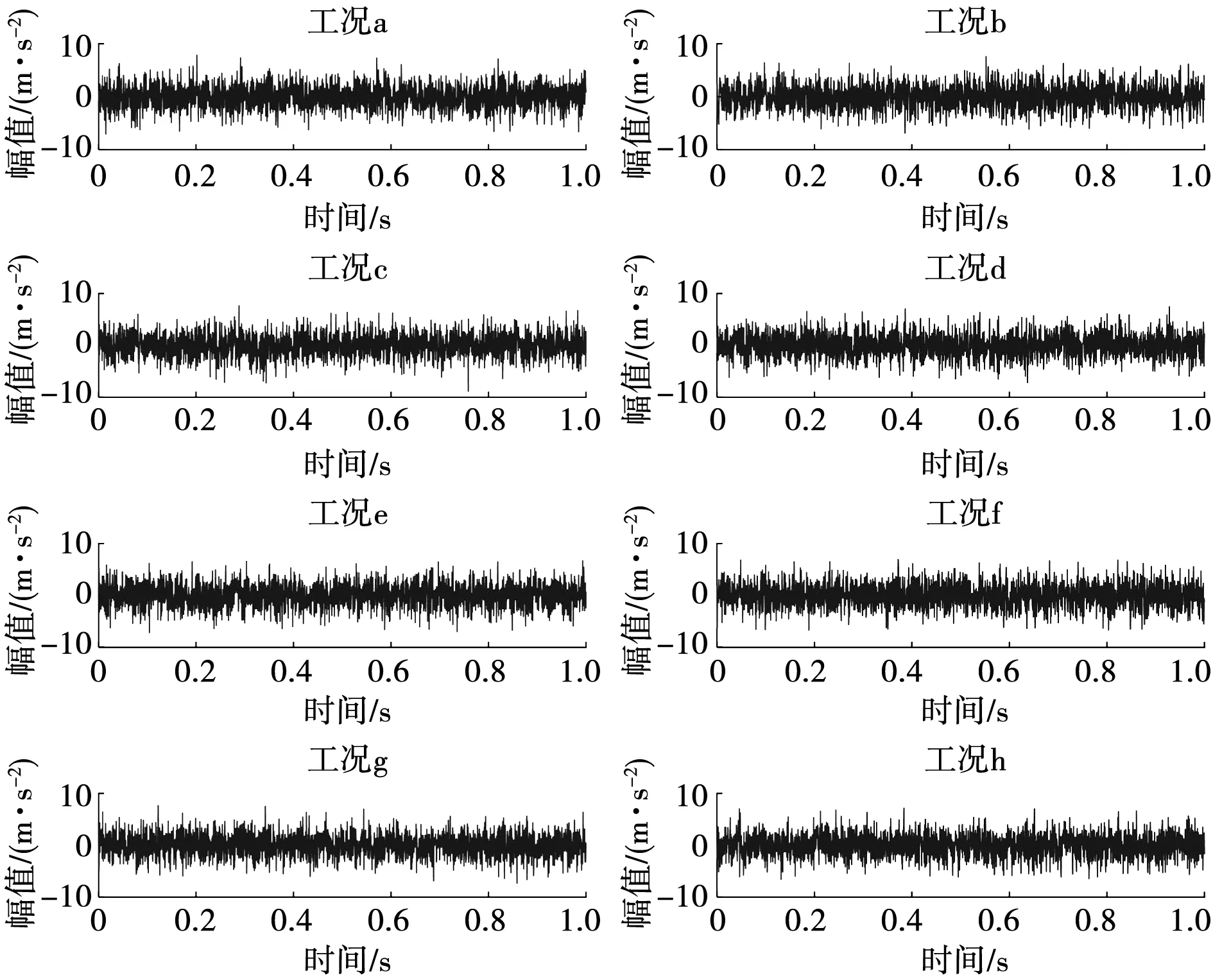
图9 电机轴承8种运行工况的时域图
3.2 实际信号分析
以工况e为例,其故障特征频率计算如下:
(24)
式中:fr为转频;d和D为滚珠和节圆直径;Z为滚珠个数;α为接触角,因此求得电机轴承外圈故障特征频率约107.8 Hz,转频35 Hz。图10~图12分别为工况e振动信号的ESST时频谱、Stockwell变换时频谱和SST时频谱。
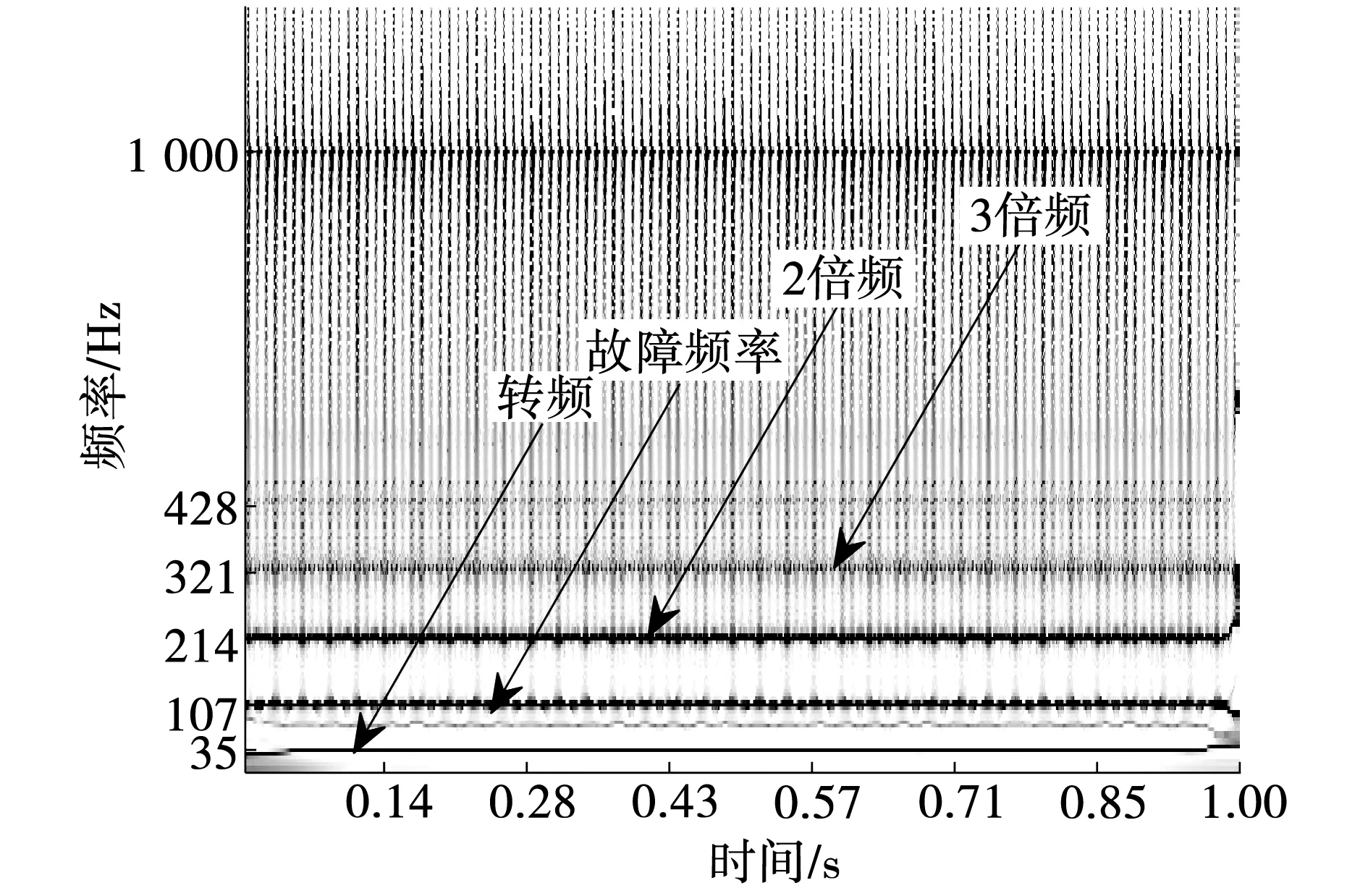
图10 实际信号的ESST时频谱图
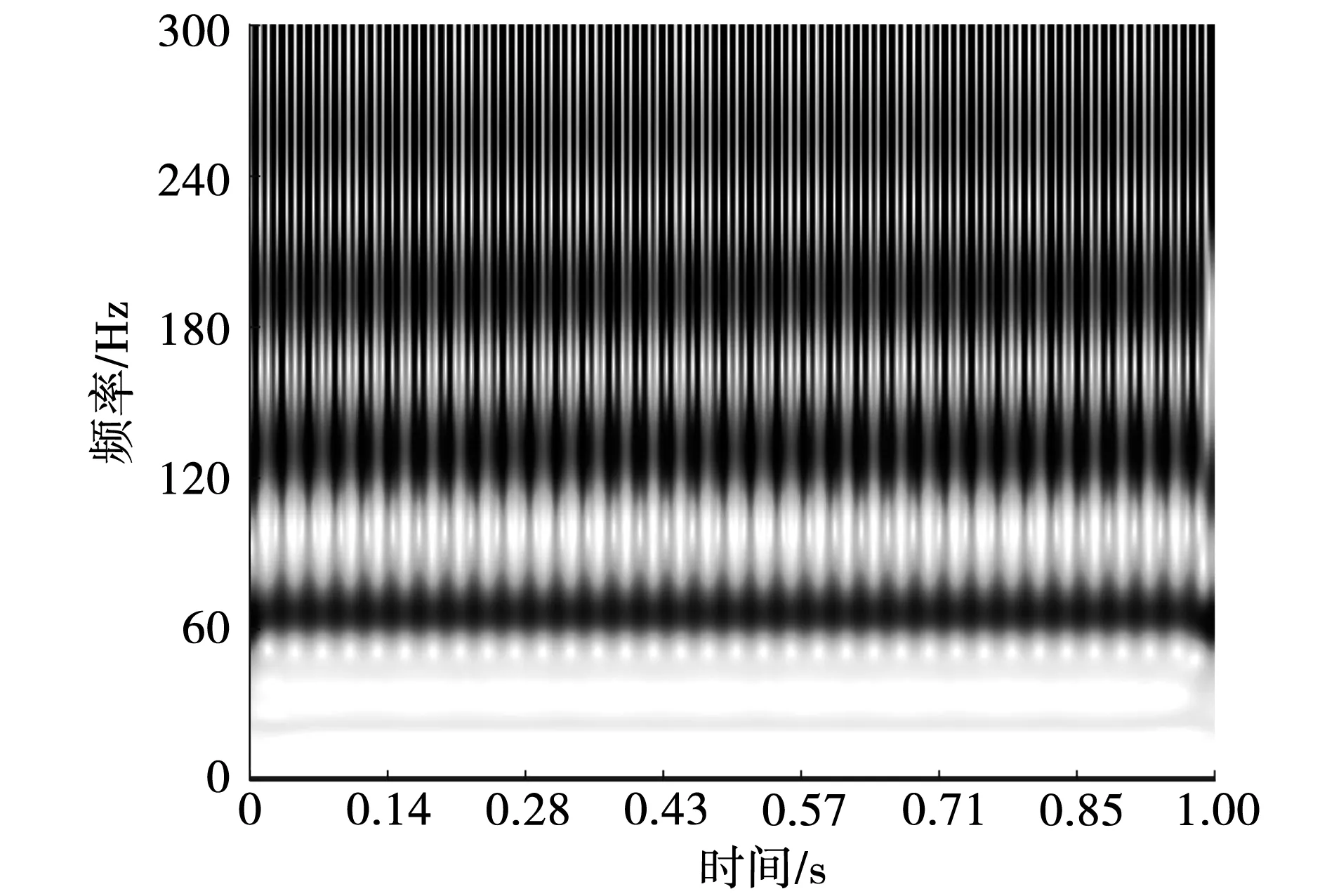
图11 实际信号的Stockwell变换时频谱图
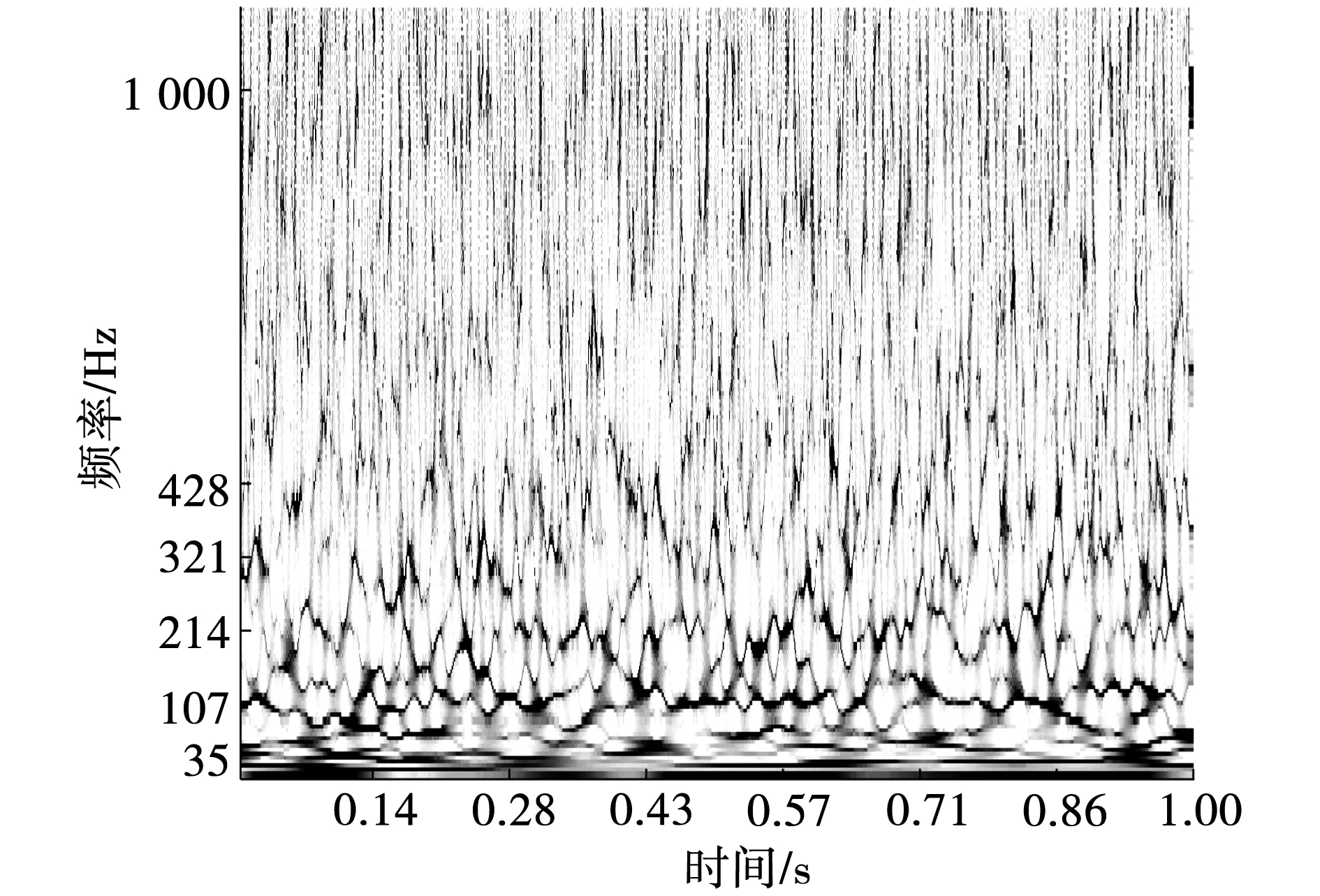
图12 实际信号的SST时频谱图
由图可知:Stockwell时频谱图的时频分辨率低,时频谱杂乱;虽然SST时频谱较ST清晰,但时频谱能量发散,受噪声干扰较严重;而ESST时频谱脊线较明显,故障特征频率较清晰,时频分辨率较高,进一步验证了ESST的优越性。
3.3 工况识别与分析
本试验训练的硬件环境为i7-10700 CPU、GTX1050Ti显卡、16G内存,编程环境为MATLAB R2021b。用于工况识别的每个IDELM网络的参数如表5。
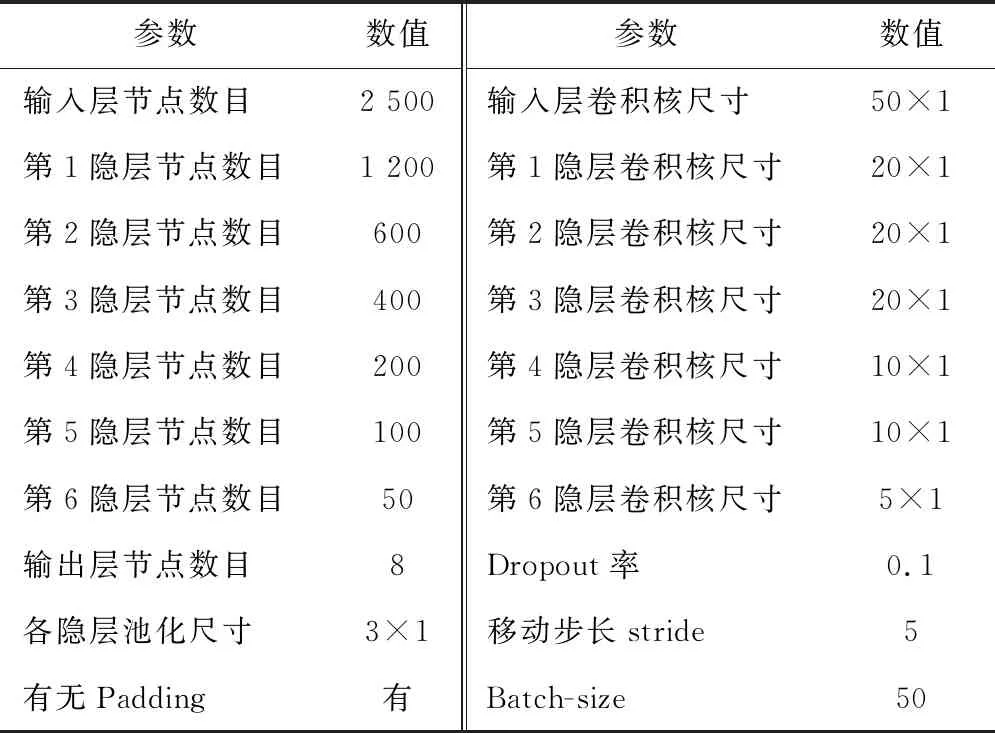
表5 IDELM参数
首先验证IEDELM的效果,采用文献[15]的深层稀疏自编码器(DSAE)、文献[16]提出的深层降噪自编码器(DDAE)和文献[17]提出的和深层极限学习机(DELM)进行对比分析。各网络结构均为2500-1200-600-400-200-100-50-8,信号前处理方法均为ESST变换。表6列出了不同的网络10次实验平均工况识别率。
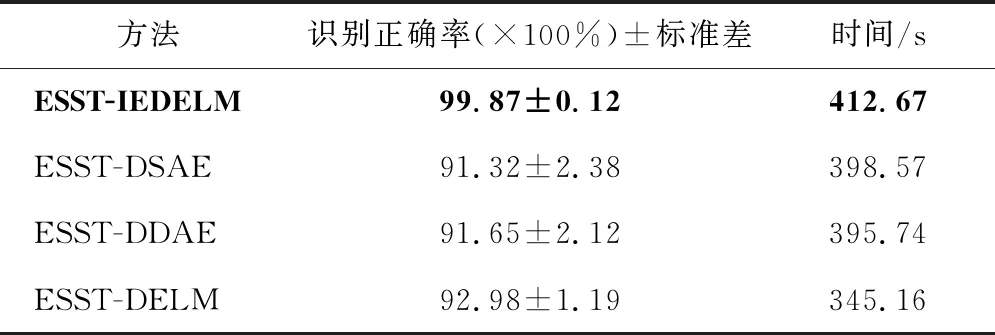
表6 不同网络的工况识别结果
由表6可知,ESST -IEDELM方法具有更高的识别准确率(99.87%),更小的标准差(0.12),即更高的训练稳定性,但其训练时间约413 s,略高于其他深层网络,这是因为IEDELM的自组织策略和集成学习方法一定程度增加了网络的训练时间,综上由于IEDELM的多种改进措施,工况识别率和识别稳定性均优于其他几种网络。其次验证ESST的效果,采用经验模态分解(empirical mode decomposition,EMD)、集合经验模态分解(ensemble empirical mode decomposition,EEMD)、完备集合经验模态分解(complete ensemble empirical mode decomposition,CEEMD)、Stockwell变换(stockwell transform,ST)、经验小波变换(empirical wavelet transform,EWT)、变分模态分解(variational mode decomposition,VMD)、同步挤压小波变换(synchrosqueezing wavelet transform,SWT)和SST等不同的信号前处理方法进行对比。表7列出不同信号前处理方法10次实验的工况识别率。
由表7,基于ESST前处理方法的电机轴承工况识别率较其他方法更高,基于EMD、EEMD和CEEMD的前处理方法受噪声干扰严重,模态混叠严重,时频谱杂乱,导致工况识别率较低;ST、EWT和VMD一定程度上改进了模态混叠的缺陷,识别效果略优于EWD、EEMD和CEEMD;SWT和SST一定程度上改进了传统时频分析方法的时频能量发散状况,效果优于ST、EWT和VMD,但抗噪能力较弱;而ESST方法使用高阶瞬时频率估计,提升了抗噪能力,识别效果最好。
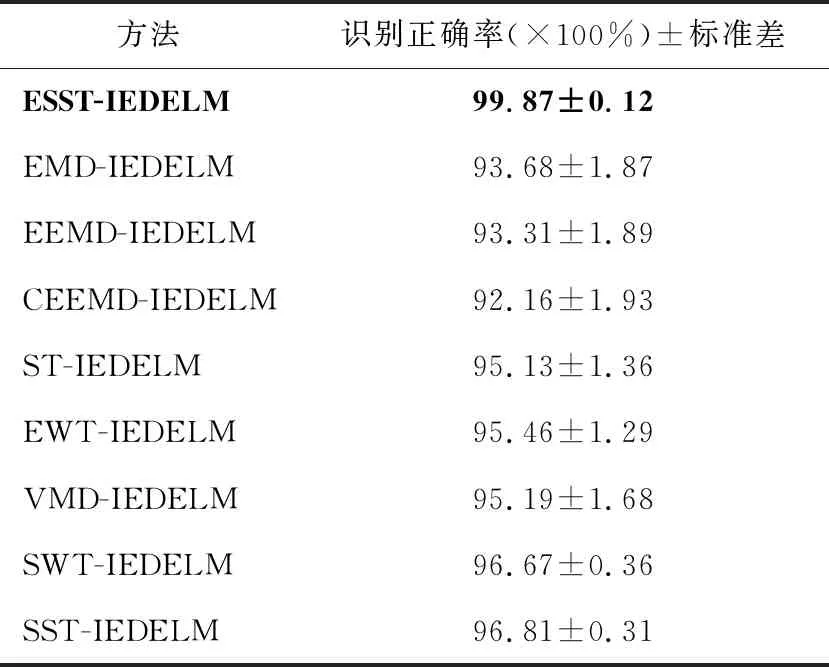
表7 不同前处理方法的电机轴承工况识别结果
ESST-IEDELM模型在每次迭代中的损失值如图13所示,可见模型的损失函数已得到收敛。
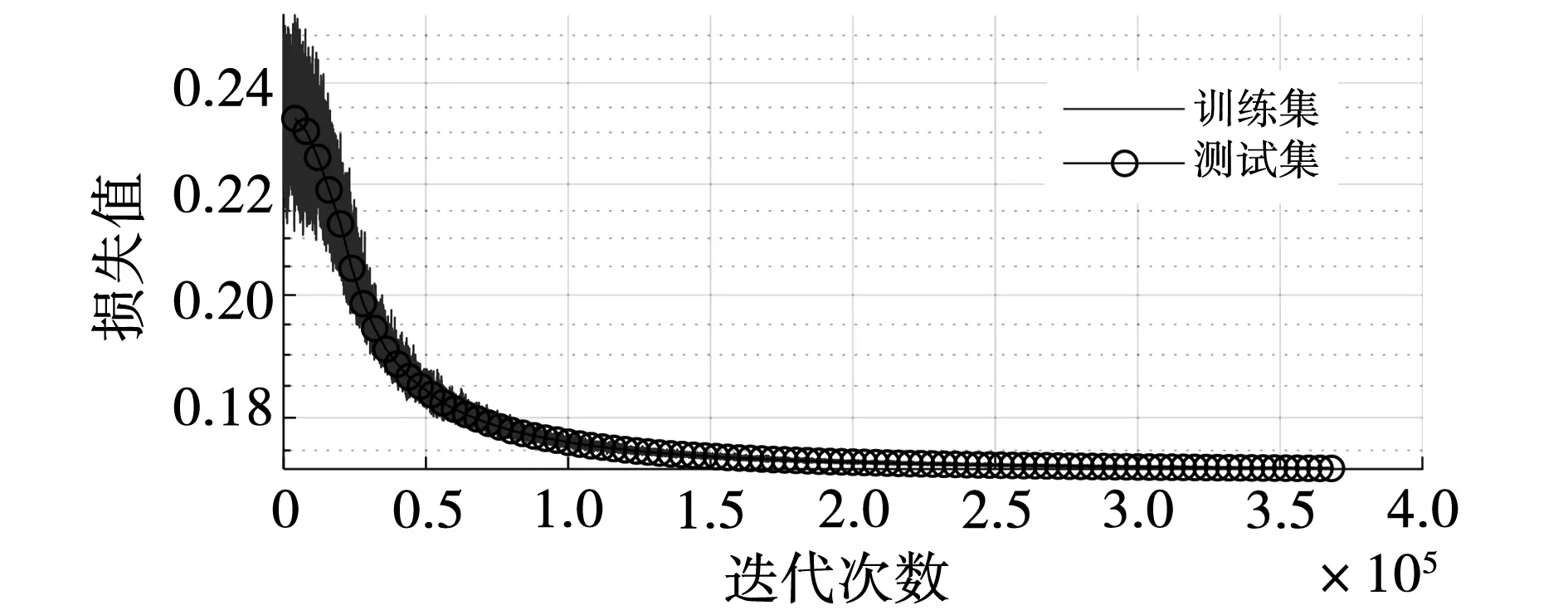
图13 ESST-IEDELM模型的训练进度图
以测试结果的假阳率和真阳率作为横、纵坐标绘制ROC曲线,AUC为ROC曲线下的面积,其值越大,代表模型的性能越好,准确率更高。以第一次测试结果为例,ROC曲线如图14所示,可知ESST-IEDELM算法模型的AUC值为0.982,具有较高的准确性,验证了提出方法的优越性。
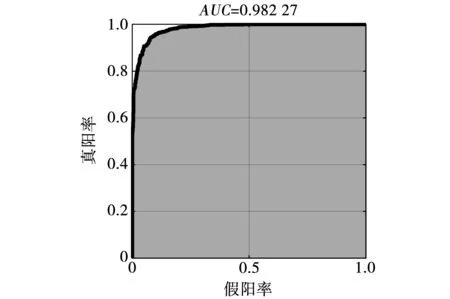
图14 第1次测试结果的ROC曲线
3.4 噪声对ESST-IEDELM模型的影响
本节进一步研究在噪声干扰下ESST-IEDELM的性能,通过添加不同信噪比(signal-to-noise ratio,SNR)的高斯白噪声进行对比实验,设置了取15、10、5 dB下的4组实验,如表8所示。相应的对比结果如表9所示,随信噪比的降低,不同模型的工况识别准确率均有所降低,但本文提出的ESST-IEDELM模型在添加不同信噪比的高斯白噪声后相比于其他方法识别率更高,进一步验证了ESST-IEDELM的优越性。

表8 实验名称及方法
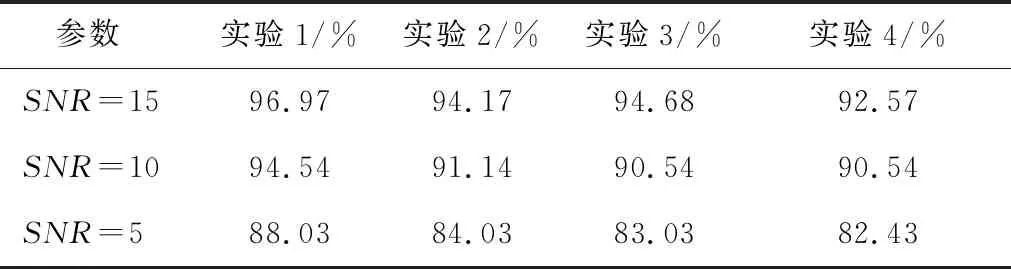
表9 对比结果
3.5 不平衡数据集下的模型工况识别效果
在实际工业中,通常正常工况下样本所占比例较故障工况样本高,因此本文进一步研究ESST-IEDELM方法在面对不平衡工况样本时的有效性,比较3种不同方法(ESST-IEDELM、SST-IEDELM、ESST-IDELM)的识别性能。设置正常与各故障工况的训练样本比例为8 000∶8 000、8 000∶6 400、8 000∶4 800和8 000∶4 000,实验共进行10次。以组4为例,定量计算3种模型在不平衡样本数据集的F1值,结果如表10所示。
由表10可知,组4中ESST-IEDELM模型的F1值较高,类似的结果在其他组中也有较为明显的体现,对比结果进一步验证了ESST-IEDELM在面对不平衡数据集的有效性。
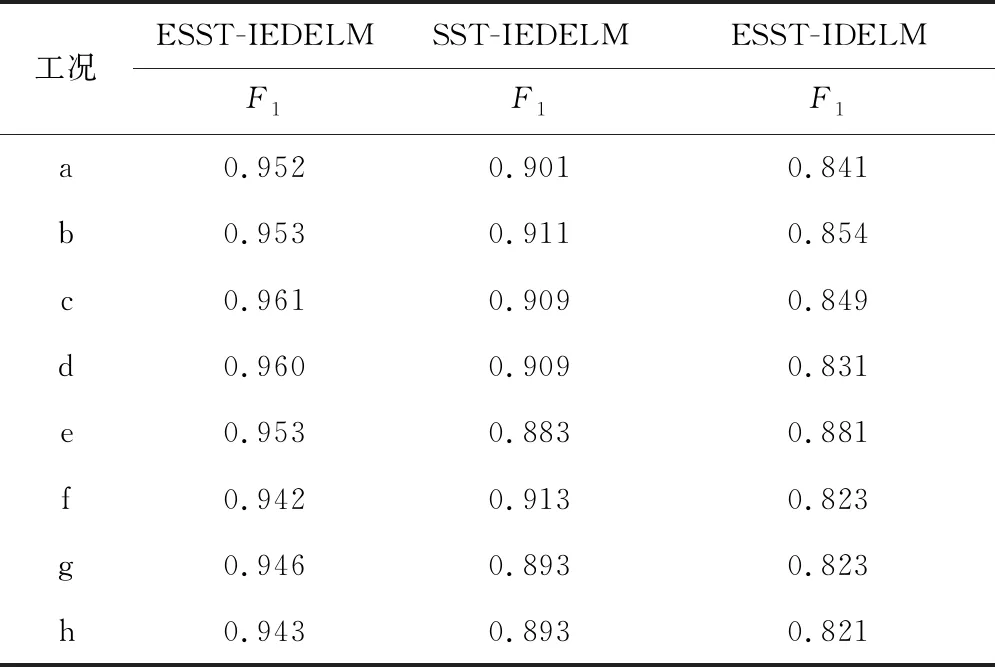
表10 组4不同方法的F1值
3.6 深层特征评价
本节进一步评价IEDELM所学习到的深层特征的质量,首先计算类间协方差Bc和类内协方差Ic。其中:Bc代表不同工况间的离散程度,Ic代表同一工况内的聚类程度,Bc越大及Ic越小表明特征具有较强的类区分度,Bc和Ic的详细计算见文献[18]。并采用文献[19]的3个评价指标对深层网络学习到的顶层特征质量进行定量描述,如下:
(25)
(26)
(27)
式中:tr()为取迹操作。3个指标结合了Bc和Ic的综合信息,计算结果如表11所示。根据评价标准,Ji(i=1,2,3)越大代表更好的工况识别结果。由表10可知,基于IEDELM模型的顶层特征的3个评价指标分别为2.914、0.813和3.869,均大于其他3种深层模型,表明IEDELM学习到的顶层特征存在着较大的Bc和最小的Ic,即存在较大的工况特征可区分度,因此更有利于工况识别。
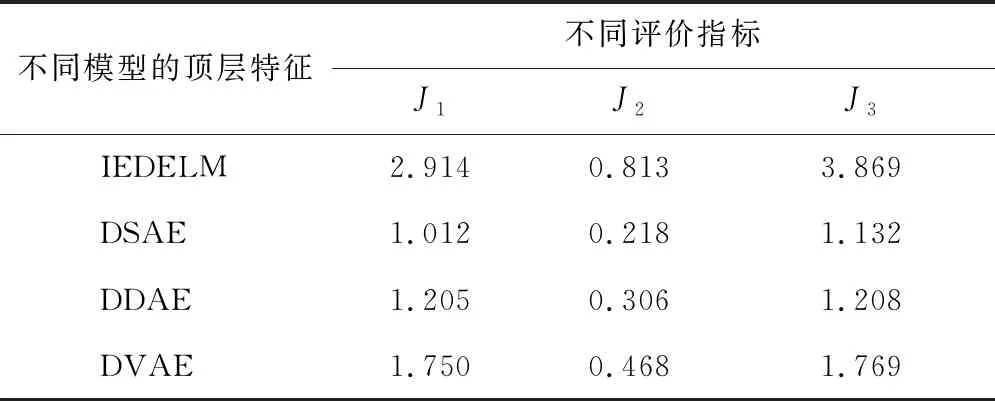
表11 不同深层模型顶层特征的定量评价
4 结 论
本文提出一种基于ESST-IEDELM的电机轴承工况识别方法,能有效地对电机轴承信号进行自动特征提取与工况辨识,主要结论如下:
1)提出的ESST通过高阶瞬时频率估计有效提高了时频谱抗噪声能力,所提取的时频谱脊线较明显,故障特征频率较清晰,时频分辨率较高,为IEDELM提供了优秀的训练样本;
2)提出的IEDELM对DELM进行了有效改进,使用卷积策略,使网络学习到的特征更具鲁棒性;引入自组织策略,使网络结构在训练过程中自适应动态变化,更适用于电机轴承工况识别;将多个IDELM进行集成,获得了比单一深度学习模型更好的工况识别效果。
