基于改进灰狼优化算法的PMSM滑模自抗扰控制
2022-12-04赵希梅陈广国金鸿雁
赵希梅, 陈广国, 金鸿雁
(沈阳工业大学 电气工程学院,辽宁 沈阳 110870)
0 引 言
永磁同步电动机(permanent magnet synch-ronous motor,PMSM)具有高效率、大扭矩惯性比、结构简单、可控性好的优点,在工业伺服系统中得到广泛应用[1]。由于PMSM本身具有时变性、非线性、强耦合的特点,当系统受到外部扰动、参数变化的影响时,传统的PID控制很难满足高精确度控制的需求[2-3]。
由我国的韩京清学者提出来的自抗扰控制(active disturbance rejection control,ADRC)一种新的非线性控制方法,因其控制过程中不需要知道控制对象的精确数学模型和对不确定因素具有强鲁棒性而得到广泛应用[4-5]。文献[6]提出了一种增强型线性自抗扰控制器,该控制器由两个线性扩张状态观测器(extended state observer,ESO)组成,对外部扰动和参数变化具有很好的抑制作用,而不需要精确的PMSM数学模型。但是传统ESO的峰值问题没有得到解决,容易影响观测精确度。文献[7]提出一种基于非线性ESO的PMSM全速范围控制策略,可以快速估计不确定因素并进行补偿,相比线性ESO提高了观测精确度,同时具有更小的峰值。文献[8]提出一种基于增益连续ESO的PMSM电流解耦控制方法,增益连续ESO克服了非线性函数fal()切换点的突变问题,具有较好的观测精确度。由于控制器参数较多,很难认为调整到最佳性能,同时,灰狼优化算法(grey wolf optimizer,GWO)因其算法简单、需要调节参数少、搜索能力强等优点备受青睐[9-10]。文献[11]提出了一种基于GWO的转矩预测控制方法,采用GWO优化了PMSM低速运行时的转矩跟踪,振动较小,实现了转速和转矩的平滑切换。但是GWO仍然存在一般元启发式算法的问题,需要平衡其局部搜索和全局搜索的能力,避免陷入局部最优,同时提高搜索速度。由于滑模控制(sliding mode control,SMC)具有对外部扰动和参数变化不敏感、快速响应的优点,本文将SMC代替自抗扰控制中的非线性状态误差反馈(non-linear state error feedback,NLSEF)来提高系统的鲁棒性。
基于此,本文提出一种基于改进灰狼优化算法(improved grey wolf optimizer,IGWO)的滑模自抗扰控制(sliding mode active disturbance rejection control,SM-ADRC)方案,抑制不确定性的影响并提高PMSM伺服系统的收敛速度。首先,设计(variable gain extended state observer,VGESO)抑制初始峰值,提高观测精确度;然后依据观测值设计滑模控制器,以此提高系统的鲁棒性和收敛速度;使用IGWO优化SM-ADRC中滑模控制部分的参数,充分发挥所设计控制器的性能。通过仿真实验证明,所提出的控制方案可以在短时间内将PMSM的转速跟踪到给定转速,抑制不确定性因素对系统性能的影响,同时也有效地削弱抖振。
1 PMSM数学模型
使用Park变换,可以得到d-q坐标下的表贴式PMSM的电压方程为:
(1)
其中:id、iq和ud、uq分别是d轴和q轴的定子电流和定子电压;Ld、Lq是d轴和q轴的定子电感,其中Ls=Ld=Lq;ψf是永磁体磁链;R是定子电阻;ωe表示转子电角速度。
表贴式PMSM的运动方程为:
(2)
其中:J是转动惯量;ω是机械角速度;Te是电磁转矩;B是粘滞摩擦系数;TL是负载转矩;p是极对数。
在id=0的解耦控制下,转矩方程为
(3)
考虑参数变化和外部扰动,表贴式PMSM的运动方程改写为
(4)
其中:b0=3Pψf/2J是电流iq的增益项;b1=B/J是转速ω的增益项;b2=1/J是负载转矩TL的增益项。Δ0、Δ1、Δ2为对应增益项的扰动。式(4)可以改写为
(5)
其中F=Δ0iq-Δ1ω-(b2+Δ2)TL是系统受到的内外扰动的总和。
2 PMSM控制系统设计
2.1 传统ADRC
ADRC是一种对系统内外未知扰动实时观测并进行补偿的控制方法,包括跟踪微分器(tracking differentiator,TD)、ESO、NLSEF三部分;一阶ADRC的结构框图如图1所示。
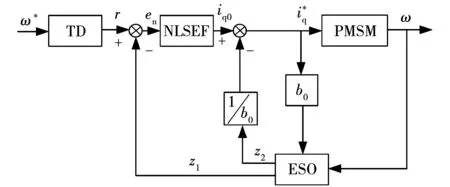
图1 一阶ADRC结构框图
TD的表达式如下:
(6)
其中:r为ω*的跟踪信号;R为速度跟踪因子。
ESO的表达式如下:
(7)
其中:z1是ω的跟踪信号;z2是扰动总和F的观测值;β1、β2是误差校正因子。
NLSEF的表达式为:
(8)
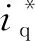
(9)
其中:ex是误差;αx是非线性因子;δx是滤波因子;x=r、ω、n。
2.2 SM-ADRC设计
传统ADRC待调节的参数较多,同时由于PMSM速度控制是一阶的,不需要二阶变量,为了简化设计,所以设计过程中舍弃TD部分。基于IGWO的PMSM控制系统框图如图2所示。
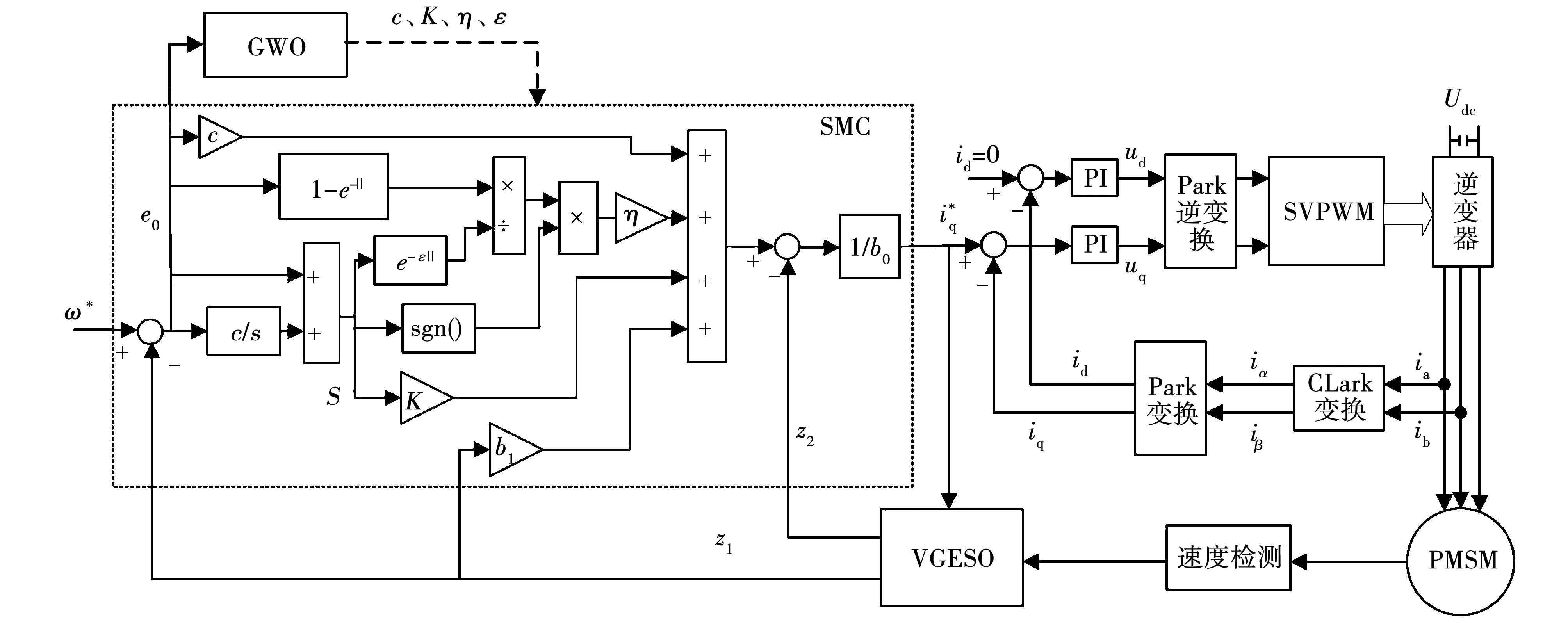
图2 基于IGWO的PMSM控制系统框图
由于fal(ex,αx,δx)是分段函数,是通过切换条件来切换不同的表达式,且切换点的不可导性会使得动态增益出现突变,严重时会导致观测出来的状态量发生抖振,为了克服这一问题,这里采用一种误差校正函数fac(),其表达式为
(10)
其中λ为误差增益。根据反正切函数特性,该函数可以不用再根据ex的大小切换表达式,具有连续可导性。为了获得“大误差小增益,小误差大增益”的校正特性,选取αx=0.5,λ=5 000。
(11)
其中r(t)为变增益,定义为
(12)
VGESO的结构框图如图3所示。
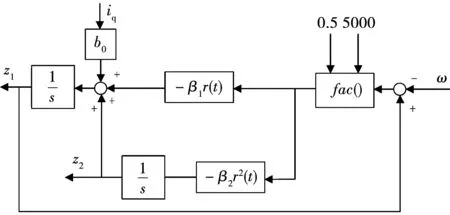
图3 VGESO的结构框图
在式(11)中,令
(13)
于是式(11)可以改写为:
(14)
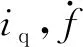
(15)
令eF=z2-x2,L1=β1G1,L2=β2G2,根据式(14)和式(15)得:
(16)
令γ1=eω,γ2=eF-L1eω,得:
(17)
当忽略扰动F时,上式的特征方程为
λ2+L1λ+L2=0。
(18)
根据Hurwitz定理,二阶系统稳定的充分必要条件是L1>0和L2>0。
因为
(19)
则G1、G2>0,推导出当β1、β2>0时,L1和L2大于0,VGESO是稳定的。
当系统存在干扰总和F时,系统存在稳态误差。系统达到平衡状态之后,有:
(20)
观测器的稳态误差可以表示为
(21)
因此只要β2比ω0大很多,ESO的观测误差就会很小,以满足精确度要求。其中ω0为VGESO的带宽。
本文,将SMC代替ADRC中的NLSEF,提高此环节的鲁棒性。为了抑制抖振,采用积分型滑模面
(22)
式中:e0=ω*-z1是期望角速度(ω*)和角速度观测值(z1)之间的误差,c是大于0的任意变量。用z2代替扰动总和F,结合式(5)得
(23)
使用改进型趋近率
(24)

结合式(23)和式(24),得
(25)
稳定性分析:Lyapunov函数为
(26)
则
(27)
因此系统稳定的。
2.3 IGWO设计
GWO是最近受灰狼的包围行为和狩猎行为启发而提出来的优化算法,同时GWO具有等级制度。根据灰狼的社会行为划分了4个等级,其中α狼为领导狼,代表最好的最优解;以及β狼和δ狼,分别代表第2个和第3个最优解,在决策过程中为领导狼提供帮助;而γ狼按照命令行动。GWO的各狼等级如图4所示。
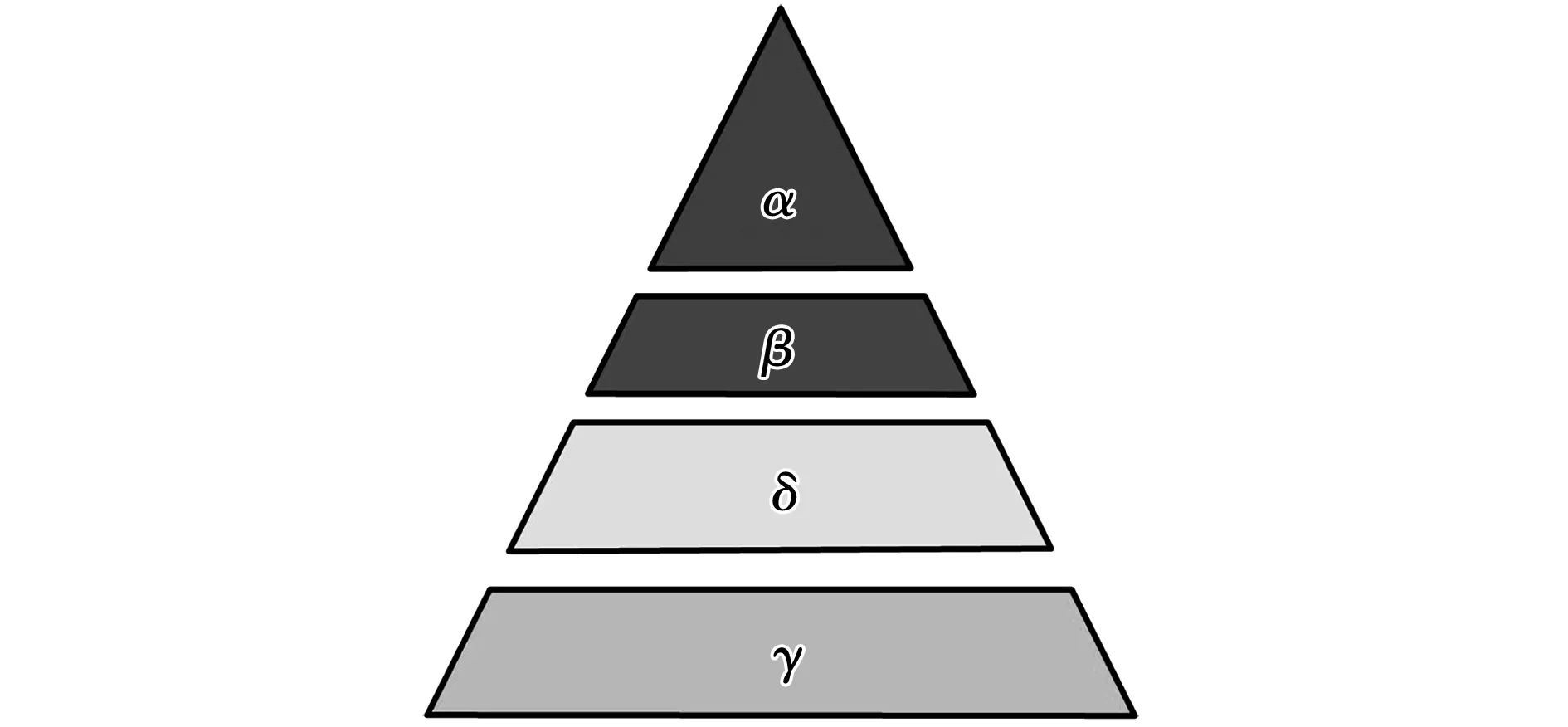
图4 灰狼等级图
包围行为可以用数学模型表示为:
D=|CXp(t)-X(t)|;
(28)
X(t+1)=Xp(t)-AD。
(29)
其中:Xp(t)和X(t)分别代表猎物和灰狼的位置,D为猎物与灰狼的距离,X(t+1)为灰狼根据猎物位置进行包围行为的下一个位置。A和C为控制系数,为:
A=2ar1-a;
(30)
C=2r2。
(31)
其中:r1和r2为[0,1]的随机变量。收敛因子a在迭代过程中从2线性下降到0。
狩猎行为可以用数学模型表示为:
(32)
(33)
(34)
定义目标函数为
(35)
其中N为采样总数。
由于,收敛因子a是线性递减的,没有充分发挥灰狼的探索能力,容易造成早熟问题。所以采用改进收敛因子
(36)
其中:t为当前的迭代次数;tmax为最大迭代次数;rand()为0到1的任意值。
3 系统仿真实验分析
为了验证IGWO的求解能力,本文选择5个标准测试函数,分别采用IGWO、GWO、粒子群(particle swarm optimization,PSO)进行求解。标准测试函数如表1所示。

表1 标准测试函数
在MATLAB上对进行测试,最大迭代次数设置为500,得到如图5所示的函数值收敛曲线。

图5 函数值收敛曲线
从函数值收敛曲线可以得出,在5种标准测试函数测试下,IGWO的收敛速度比GWO、PSO更快,同时IGWO的求解精确度也比GWO、PSO的更高。
采用Link-RT半实物仿真平台进行实验验证,半实物仿真平台如图6所示。主要包括上位机、Link-BOX实时仿真机、扭矩传感器、伺服电机、伺服驱动器等。

图6 半实物仿真平台
为了验证本文的改进SM-ADRC的有效性,PMSM伺服系统分别采用ADRC、传统SM-ADRC(传统滑模+ESO)、改进SM-ADRC进行实验对比。基础条件可以设置为:逆变器的给定电压为Udc=311 V;SVPWM的开关切换频率设置可以为f=10 kHz,采样周期Ts=10 μs,相对误差可以设置为0.000 1。PMSM的参数如表2所示。
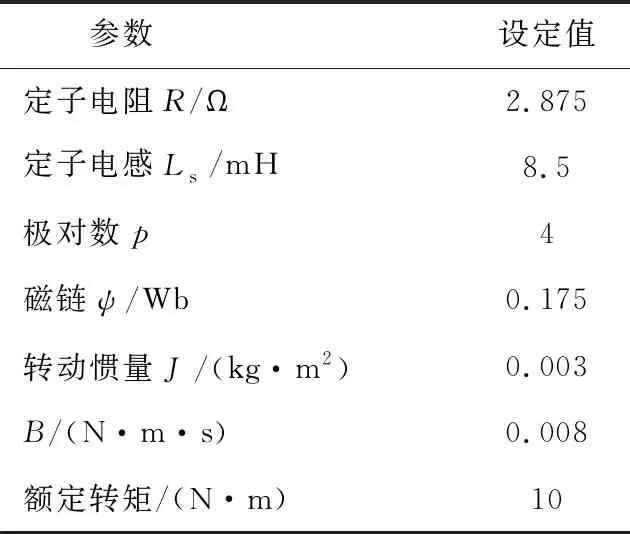
表2 电机参数
为了充分发挥控制器的性能,采用IGWO分别对ADRC、传统SM-ADRC、改进SM-ADRC的参数进行优化,优化流程如图7所示。IGWO的最大迭代次数tmax=100,运行程序得到ADRC的控制参数为:R=6 500,αr=0.4,δr=0.01,β1=8 500,β2=500 000,αω=0.9,δω=0.01,β3=5 000,αn=0.9,δn=0.01;传统SM-ADRC的控制参数:c=50,η=204.09,k=326.21,β1=8 500,β2=500 000,αω=0.9,δω=0.01。改进SM-ADRC的控制参数:c=2 527.4,ε=0.1,η=1 451,K=0.3,β1=8 500,β2=90 000 000。
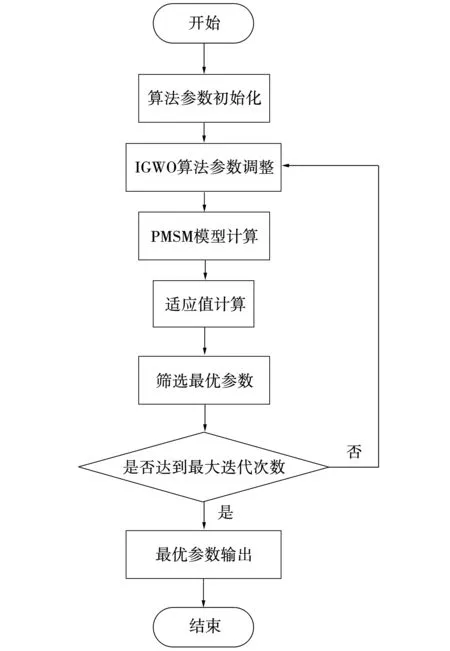
图7 IGWO算法参数优化流程图
工况一,为了验证改进SM-ADRC的跟踪性能,PMSM伺服系统空载,在0时刻给定转速设置为1 000 r/min,0.2 s时刻给定转速设置为1 500 r/min,3种控制方法的空载转速响应曲线如图8、图9、图10所示。从图8可知,在空载的情况下,ADRC转速上升到1 000 r/min时的超调为3 r/min,在0.07 s时刻电机转速稳定在设定值1 000 r/min;ADRC转速上升到1 500 r/min时的超调为1 r/min,在0.21 s时刻电机转速稳定在设定值1 500 r/min。从图9可知,传统SM-ADRC转速上升到1 000 r/min时的超调为1 r/min,在0.012 s时刻电机转速稳定在设定值1 000 r/min;传统SM-ADRC转速上升到1 500 r/min时的超调为0.5 r/min,在0.21 s时刻电机转速稳定在设定值1 500 r/min。从图10可知,改进SM-ADRC转速在接近1 000 r/min时趋近速度降低,没有出现超调,在0.009 s时电机转速能稳定在1 000 r/min;改进SM-ADRC转速在接近1 500 r/min时趋近速度降低,又没有出现超调,在0.21 s时电机转速能稳定在1 500 r/min。说明空载情况下,改进SM-ADRC下PMSM的速度可以快速跟踪设定值,同时有效地抑制了峰值问题,没有出现超调。
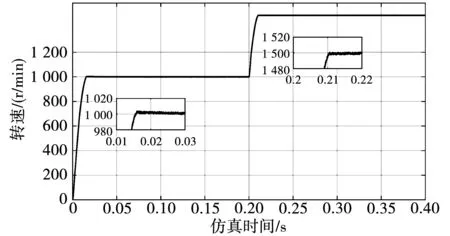
图8 ADRC空载转速响应曲线
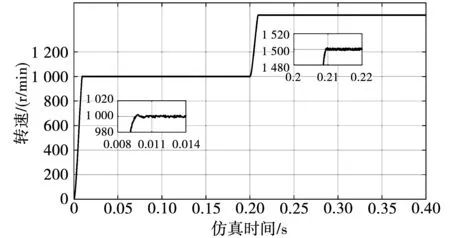
图9 传统SM-ADRC空载转速响应曲线
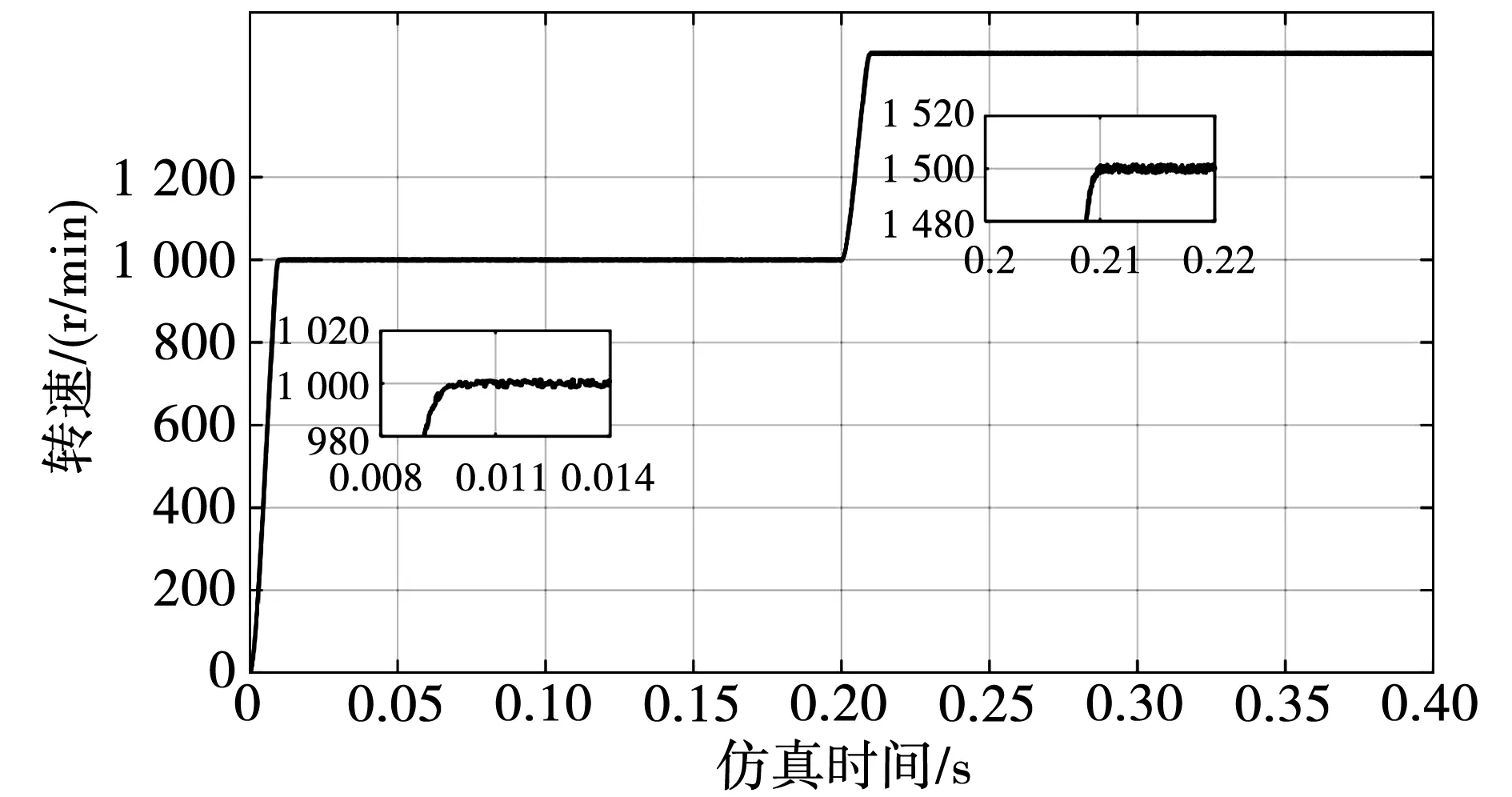
图10 改进SM-ADRC空载转速响应曲线
工况二,为了验证改进SM-ADRC的抗干扰能力,初始给定转速设置为1 000 r/min,在0.2 s时刻加10 N·m的固定负载转矩,3种控制方法的负载转速响应曲线如图11、图12、图13所示。从图11、图12、图13可知,施加10 N·m固定负载转矩后,ADRC的转速下降到959.8 r/min,在0.25 s才回到设定值;传统SM-ADRC的转速下降到980 r/min,在0.203 s转速回到设定值;改进SM-ADRC的转速下降到982 r/min,在0.203 s转速就回到了设定值。说明改进SM-ADRC具有更好的抗干扰能力。
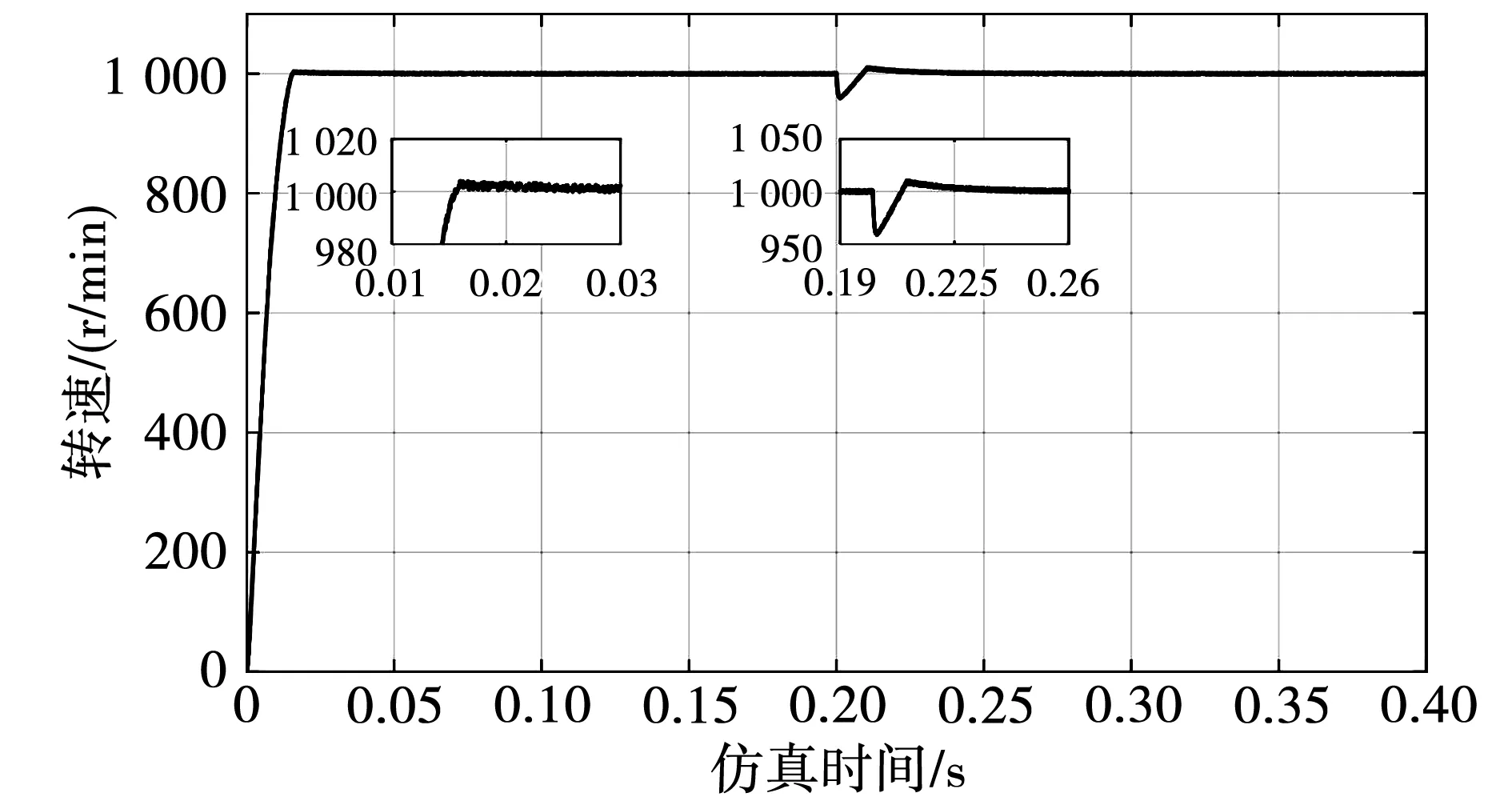
图11 ADRC负载转速响应曲线
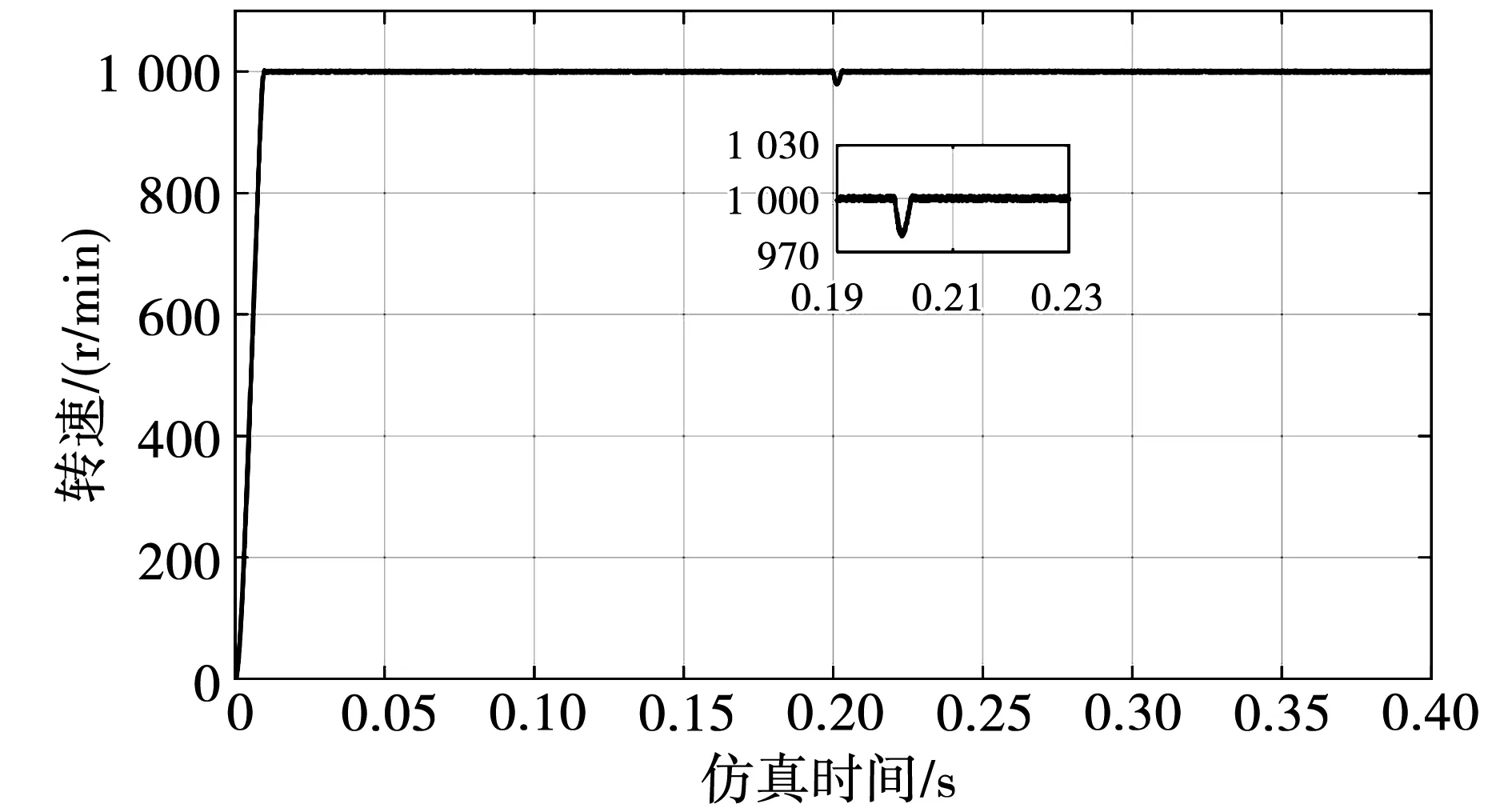
图12 传统SM-ADRC负载转速响应曲线

图13 改进SM-ADRC空载转速响应曲线
工况三,在工作环境发生变化时,PMSM的内部参数会受到外界因素的影响,为了验证改进SM-ADRC在参数变化之后转速的跟踪性能和抗干扰能力,将控制器中的电机参数(J和B)调整为原来的2倍,在0时刻给定转速设置为1 000 r/min;然后在0.2 s处,对PMSM施加10 N·m的固定负载扰动,得到3种控制方法的转速响应曲线如图14、图15、图16所示。从图14可知,ADRC转速的超调为3 r/min,在0.06 s才稳定在设定值;ADRC在受到10 N·m的固定负载转矩后,转速下降到959.4 r/min,在0.26 s时转速才回到设定值。从图15可知,传统SM-ADRC的超调为0.5 r/min,振荡0.004 s后才达到稳定;传统SM-ADRC在受到10 N·m的固定负载转矩后,转速下降到982 r/min,在0.201 s时转速才回到设定值。从图16可知,改进SM-ADRC转速没有超调,且在0.01 s就稳定在设置值;改进SM-ADRC在受到10 N·m的固定负载转矩后,转速下降到984 r/min,之后迅速回到设定值,没有振荡和稳态误差。说明改进SM-ADRC在电机参数发生变化之后,相比ADRC和传统SM-ADRC超调小,对负载转矩扰动的响应速度快且不造成振荡,对参数变化具有很好的抑制作用。
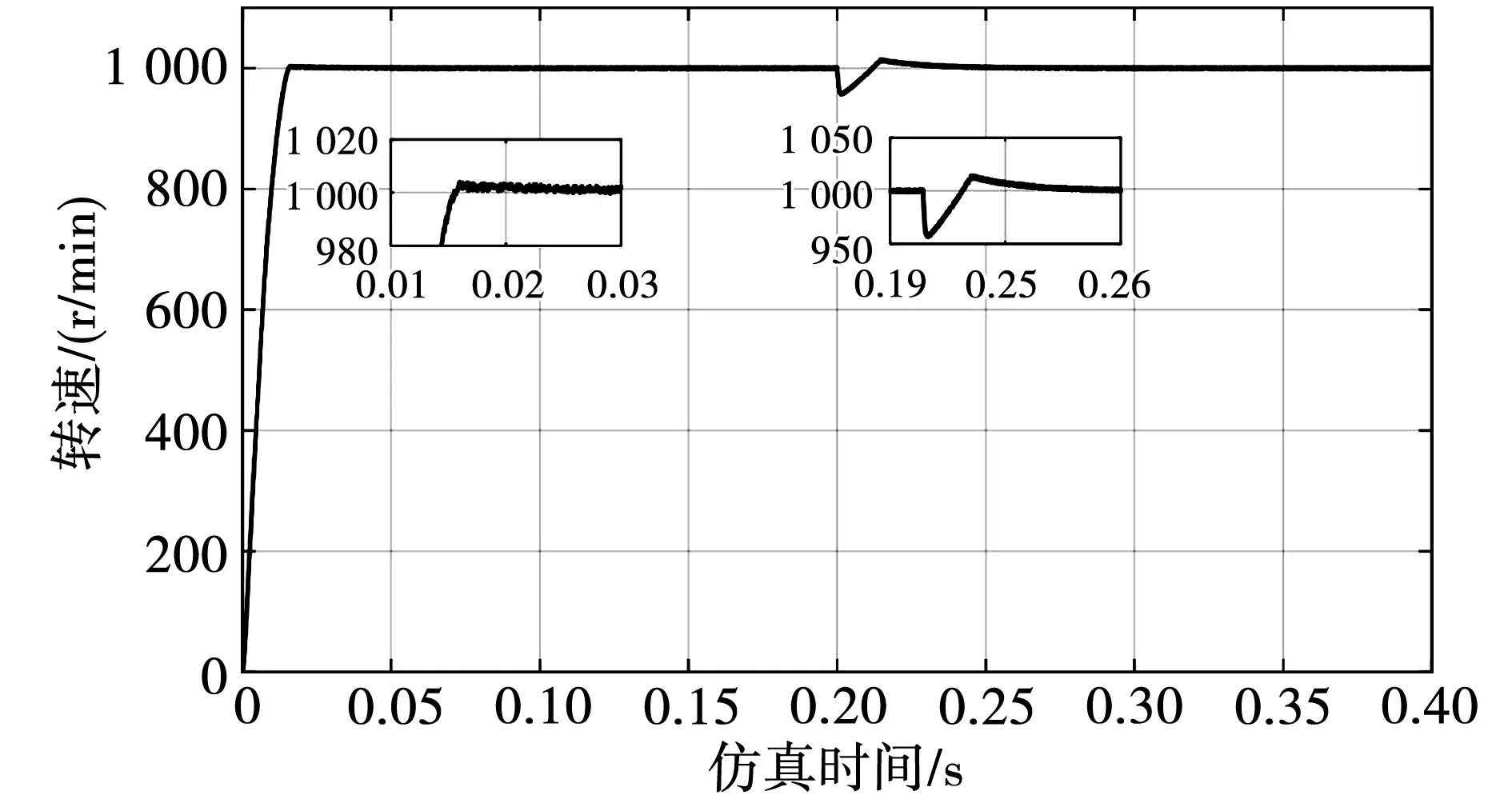
图14 ADRC参数变化转速响应曲线

图15 传统SM-ADRC参数变化转速响应曲线
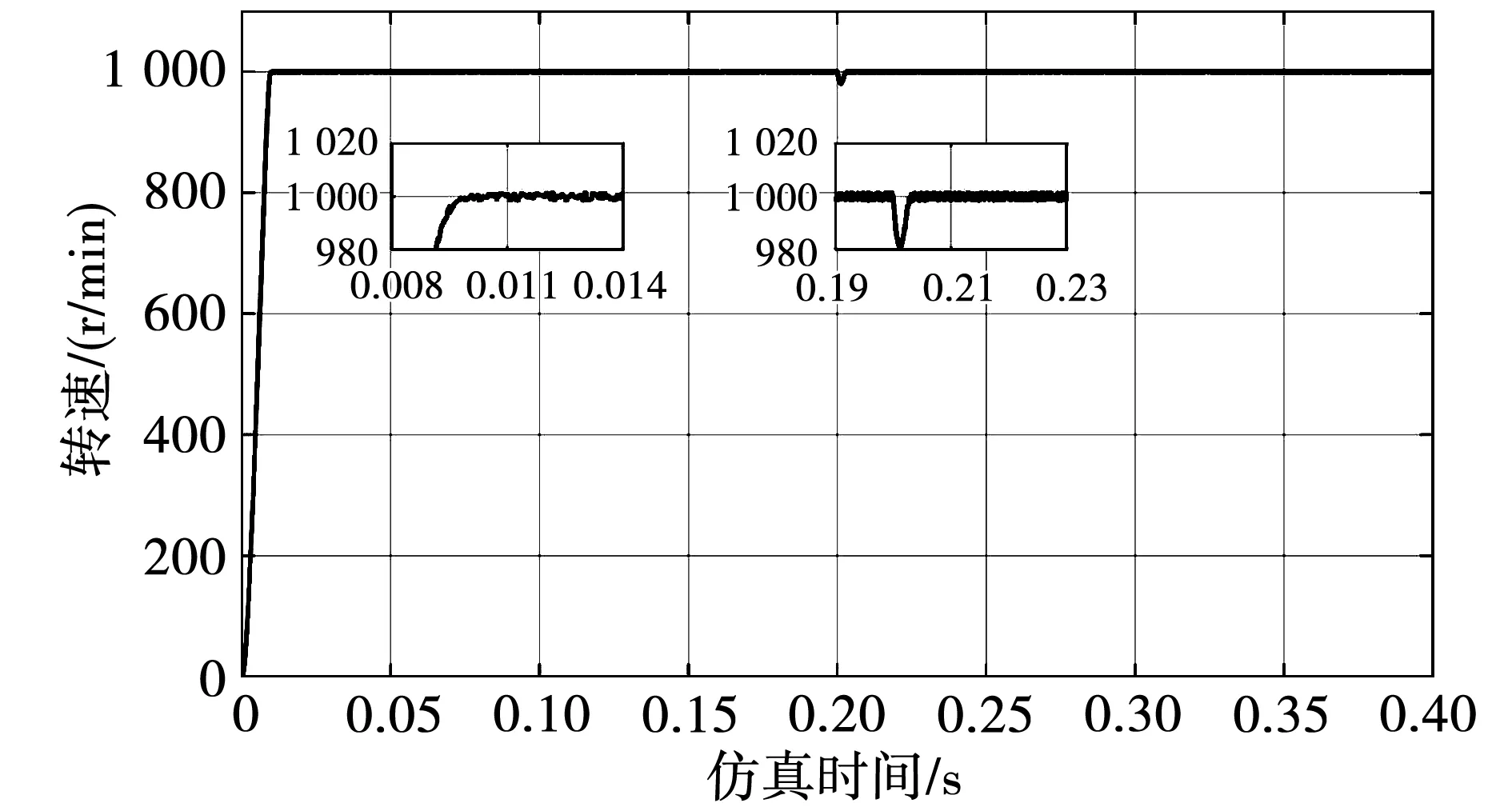
图16 改进SM-ADRC参数变化转速响应曲线
4 结 论
为了提高PMSM伺服系统的抗干扰能力,本文提出了一个基于IGWO的改进SM-ADRC方法。采用VGESO观测PMSM伺服系统所受到的不确定因素,同时抑制峰值问题对观测精确度的影响;采用SMC代替NLSEF提高了控制系统的鲁棒性。然后用IGWO对参数进行优化,充分的显示出本文的改进SM-ADRC比ADRC、传统SM-ADRC具有更好的鲁棒性,为实际的伺服系统应用提供了新方法。
