基于Hadamard 矩阵的最优局部修复码构造

王 静，田松涛，雷 珂，王相隆，任亚倩

(1. 长安大学信息工程学院 西安 710064；2. 西安邮电大学通信与信息工程学院 西安 710199)

随着全球互联网的全面普及，海量数据随之产生，如何高效地管理和可靠地存储海量数据成为当前的研究热点。海量数据主要采用分布式存储系统，为了维护系统的可用性和可靠性需引入冗余策略，最常见的冗余策略有复制策略和纠删码策略[1]，但都存在一定的局限性。随后，文献[2]将网络编码应用到分布式存储系统中，提出了再生码的概念。再生码虽然在一定程度上减小了修复带宽开销，但修复故障节点过程中需连接大量存活节点，增加了系统的磁盘I/O 开销。

为了解决上述问题，文献[3]提出了局部修复码(locally repairable codes, LRC)，有效降低了故障节点的修复局部性。文献[4]研究了信息位具有局部性和可用性的局部修复码的最小距离限，但关于修复局部性的边界条件没有研究。进一步地，文献[5-6]分别研究了局部修复码的构造并且协作局部修复码，降低了存储开销并降低了修复局部性。文献[7]研究了局部性为2 且可用性不等时的局部修复码。

最小距离和码率是衡量局部修复码性能的两个主要性能指标[8]，其中最小距离最优的局部修复码一般简称为最优局部修复码。文献[9]利用射影平面和仿射平面理论构造了3 种局部性和可用性相等的局部修复码，达到了最优最小距离边界。基于部分几何构造的最优局部修复码[10]，通过交换点集和线集的关联结构得到部分几何的对偶，进而构造局部性和可用性不等的局部修复码。基于Gilbert 方法的最优二元单校验局部修复码[11]，通过结合循环置换矩阵构造了一种新的LDPC 码，将其与单位矩阵级联形成校验矩阵，进而构造出满足最小距离界的二元单校验局部修复码。这3 种构造出的局部修复码都可达到最优最小距离边界，但是码率较小。

除最小距离和码率之外，在局部修复码中也考虑维度这一参数。有学者基于生成矩阵、校验矩阵和图论相关理论构造局部修复码来提高码率，但都没有分析维度是否达到维度最优的边界条件。文献[12]使用组合设计构造了最优二元局部修复码，运用BIBD 和DBBD 区组设计构造出的局部修复码在码率上更优，但码长略大。文献[13]使用打包设计构造了最优局部修复码，限制了码长和维度的参数条件，无法灵活地构造不同情况下的局部修复码。文献[14]构造了最优单校验二元局部修复码，但其维度没有达到维度最优的边界条件。利用图论相关理论来构造局部修复码，主要是从二分图的角度出发构造二元局部修复码[15-16]，虽然能达到最优最小距离，但是构造算法略复杂。

针对以上问题，本文提出一种基于Hadamard矩阵的最优局部修复码的构造方法。首先基于Hadamard 矩阵构造局部修复码的校验矩阵，通过校验矩阵构造局部修复码，构造的局部修复码能达到最优最小距离界，但是维度没有达到最优维度边界条件。为了进一步提高维度，将校验矩阵中的关联矩阵0 和1 元素互换得到新的关联矩阵，通过和新的关联矩阵级联进行扩展，构造的扩展局部修复码不仅能达到最优最小距离界，且能达到维度最优的边界条件。此外，基于Hadamard 矩阵构造的扩展局部修复码的码率也更逼近局部修复码最优码率的边界，参数选择更加灵活。

局部修复码作为广义上的纠错码，适用于分布式存储系统。分布式存储系统中存储的文件采用局部修复码进行编码，并将编码后的信息存于存储节点中。当有部分存储节点故障，则可以利用其余存活节点修复故障节点，实现分布式存储系统中数据的可靠存储。本节主要介绍局部修复码的一些相关原理。

1.1 ( r,t)可用性

定义1[8]在有限域Fq上的 [n,k,d]q线性分组码中，给定[n]={1,2,···,n} ， 码字c=(c1,c2,···,cn)。如果其中一个编码符号ci具 有局部性r和可用性t，需满足下列条件：

称φj(i)(j∈[t])为ci的修复集合。如果局部修复码的所有信息位码元都具有 (r,t)可用性，那么称该码为具有 (r,t)可 用性的局部修复码，记作(n,k,r,t)iLRC。若每个信息位码元的每个修复集只有一个校验位码元，则这个码称作单校验 (n,k,r,t)iLRC。本文主要研究单校验 (n,k,r,t)iLRC，该码由关联矩阵和单位矩阵拼接而成，其中关联矩阵的行重为局部性r，列重为可用性t。

1.2 最小距离

定理1[10]若一个线性分组码C是信息位具有局部性r和可用性t的局部修复码，最小距离应满足：

定理2[13]若局部修复码的所有信息位码元的每一个修复集中只含有一个校验位，且该单校验(n,k,r,t)iLRC 的最小距离满足：

1 局部修复码相关概念

称达到边界(2)的局部修复码是最小距离最优的单校验(n,k,r,t)iLRC。

1.3 码率和维度

一般地，每个码的信息位个数k与码元数n之间的比值称作码率，用R=k/n表示。

定理3[17]若 (n,k,r,t) L RC 具有 (r,t)可用性，且该码码率满足：

则达到边界(3)的局部修复码的码率最优。

定理 4[18]特别地，可用性t=2的最优码率的(n,k,r,t=2)单校验局部修复码满足的码率边界条件为：

定理 5[19](维度C-M 边界限)在有限域GF(q)中的(n,k,r)单校验局部修复码的维度应满足：

2 最优局部修复码的构造

2.1 基于Hadamard 矩阵的局部修复码构造

构造基于Hadamard 矩阵的局部修复码，关键在于构造局部修复码的校验矩阵。局部修复码的校验矩阵用H=[M|I]表 示，I是单位矩阵，单位矩阵的列对应局部修复码的校验位符号；M是对应的关联矩阵，关联矩阵的列对应信息位符号。码字和校验矩阵的关系为c·H⊥=0，通过此关系可知每个信息位码字的修复集，一个基于校验矩阵构造的具有可用性(r,t)的 局部修复码，它的关联矩阵的行重r用来保证局部性，列重t用来保证可用性。

本节主要基于Hadamard 矩阵构造关联矩阵，关联矩阵级联单位矩阵生成校验矩阵，通过校验矩阵来构造局部修复码。

定义2k′阶 方阵Hk′，若其元素为1 或-1，且满足：

称Hk′为k′阶 Hadamard 矩阵，其中Ik′是k′阶单位阵。

若Hk′首 行首列均为全1 向量，则该Hk′为标准Hadamard 矩阵。本文所涉及的Hadamard 矩阵均为标准Hadamard 矩阵。

5) 将矩阵H(2k′-1)×(4k′-2)作为局部修复码的校验矩阵，构造得到(n=4k′-2,k=2k′-1,r=k′,t=k′)局部修复码，其中可用性t为2 的倍数。

推论1 构造1 中(n=4k′-2,k=2k′-1,r=k′,t=k′)局部修复码为最小距离最优的局部修复码，且码的最小距离d=t+1。

证 明：将 (n=4k′-2,k=2k′-1,r=k′,t=k′)局部修复码的参数代入边界条件(2)，有：

因 为k′=t，则d≤t+1。 又 根 据 式(1)得d≥t+1， 所以d=t+1，可得到基于Hadamard 矩阵构造的局部修复码的最小距离d=t+1，满足边界条件(2)，则该码是最小距离最优的局部修复码。

构造1 中的局部修复码的码率R=n k= 1

2，没有达到式(3)中最优码率的边界条件，故该码不是码率最优的局部修复码。

例1 令k′=4，得到方阵：

利用步骤 2) 可得到M8×8， 将M8×8的首行和首列全部删除，得到一个7 阶的关联矩阵M7×7：

2.2 基于Hadamard 矩阵的扩展局部修复码构造

上述基于Hadamard 矩阵构造的局部修复码的局部性和可用性相等，且能够达到最优最小距离界，但是该局部修复码的码率较小，没有达到维度最优的边界条件。为了进一步提高码率和维度，将上述构造中的关联矩阵M(2k′-1)×(2k′-1)进行扩展，得到码率更高并且维度最优的扩展局部修复码。

构造2 基于Hadamard 矩阵的扩展局部修复码的具体构造步骤如下。

1) 首先将Hadamard 矩阵的1 元素全部换为0 元素，-1 元素全部换为1 元素，得到一个k′阶方阵，记为Mk′×k′；

2) 根据k′阶 方阵Mk′×k′构造：

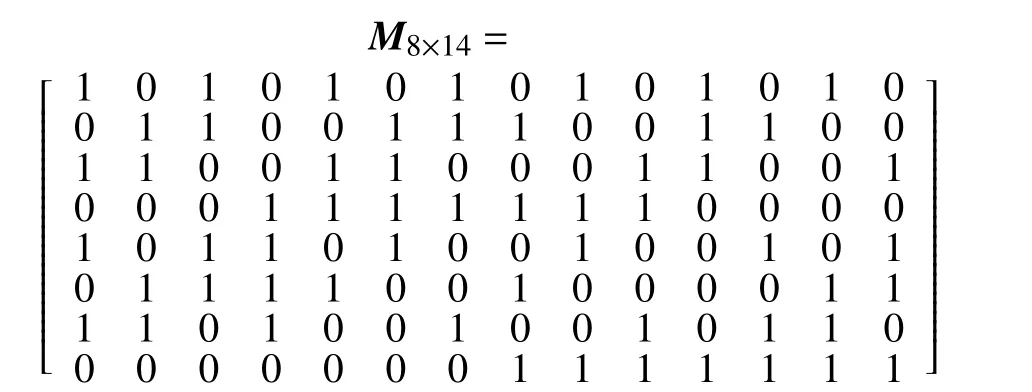
最后将M8×14作为扩展局部修复码的关联矩阵，和 单 位 矩 阵I8级 联 生 成 校 验 矩 阵H8×22=[M8×14|I8]， 由 此 可 构 造 出 单 校 验(n=22,k=14,r=7,t=4)局 部修复码，此码的最小距离d=5，码率R=7/11，与构造1 相比，有效地提高了局部修复码的码率。

故障节点的修复方法为：若信息位c1发生故障，由c·HT=0 可知，信息位c1可 根据c1=c15-c3-c5-c7-c9-c11-c13=c17-c2-c5-c6-c10-c11-c14=c19-c3-c4-c6-c9-c12-c14=c21-c2-c4-c7-c10-c12-c13进 行修复，那么信息位c1的修复集可表示为φ1={3,5,7,9,11,13,15} ，φ2={2,5,6,10,11,14,17} ，φ3={3,4,6,9,12,14,19} 和φ4={2,4,7,10,12,13,21}，各 个修复集都只有一个校验位符号。同理，其他信息位符号也可用相同的方法进行修复。

3 性能分析

3.1 最小距离和维度分析

推论2 构造2 得到的(n=6k′-2,k=4k′-2,r==2k′-1,t=k′)局部修复码是最小距离最优的局部修复码，且码的最小距离d=t+1。

证明：将(n=6k′-2,k=4k′-2,r=2k′-1,t=k′)局部修复码的参数代入边界条件(2)，可得：

因为k′=t，即d≤t+1。 又根据式(1)得d≥t+1，所以d=t+1，可以得到构造2 中的局部修复码的最小距离d=t+1。该局部修复码的最小距离满足边界条件(2)，则该码是最小距离最优的局部修复码。

推论3 构造2 得到的(n=6k′-2,k=4k′-2,r=2k′-1,t=k′)局部修复码是维度最优的局部修复码，且码的维度k≤4k′-2。

证明：当式(1)中最小距离d为最大值时，可以将式(5)简化如下：

将(n=6k′-2,k=4k′-2,r=2k′-1,t=k′)LRC 的参数条件代入简化的公式中，可得k≤4k′-2，对于∀k′，基于Hadamard 矩阵构造的扩展局部修复码的维度都可达到最优维度边界条件的上界。

3.2 与现有局部修复码的对比分析

基于Hadamard 矩阵构造的扩展局部修复码的码率为：

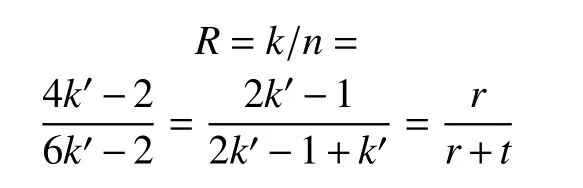
则本文构造2 中局部修复码的码率大于基于直积码构造的局部修复码码率。

表1 不同局部修复码参数对比

图1 所示为t=4时，不同局部修复码的码率R随着局部性r的变化曲线，也容易看出构造2 的码率是最逼近局部修复码最优码率界限的。

图1 t =4情 况下，码率R 的对比

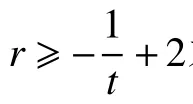
表2 不同局部修复码关于维度参数的对比

4 结 束 语

为了满足在最优最小距离边界条件下，局部修复码的维度也能达到最优，本文首先构造了基于Hadamard 矩阵的局部修复码，此局部修复码能达到最优最小距离界，但是维度没有达到维度最优的边界条件。为了提高维度，将校验矩阵中的关联矩阵0 和1 元素互换得到新的关联矩阵，通过和新的关联矩阵级联进行扩展，构造的扩展局部修复码不仅能达到最优最小距离界，且能达到维度最优的边界条件。将基于Hadamard 矩阵构造的扩展局部修复码和现有的局部修复码相比，本文的构造在码率上更逼近局部修复码最优码率的界限。

本文得到长安大学大学生创新创业训练计划项目(G202010710031)资助，在此深表感谢！