固液捆绑火箭星箭耦合分析技术研究

刘佳俊，毛玉明，博 伟，李 鑫，狄文斌

（上海宇航系统工程研究所，上海 201109）

0 引言

固液捆绑火箭，通常由液体芯级捆绑数个固体助推器组成，可充分发挥液体发动机性能高、工作时间长和固体发动机推力大、使用维护简单的各自优势。运载火箭在飞行过程中，受到平稳风、阵风、跨声速脉动压力、发动机推力等外力作用，产生随时间变化的载荷和动响应。预示火箭与卫星之间在飞行过程中的力学环境是火箭和卫星结构设计的关键之一。与单芯级火箭相比，固液捆绑火箭力学环境较复杂，火箭和卫星之间的力学环境设计是固液捆绑火箭总体设计中的难点。

星箭耦合分析是预示火箭和卫星力学环境的重要方法。星箭耦合分析主要关注火箭飞行纵、横向载荷较为严酷的工况，例如发动机开机、关机、舱段分离、跨声速抖振最大动压（Maximum Dynamic Pressure，MDP）等。星箭耦合分析通常基于星箭耦合系统的有限元模型，在特定的外力输入下，通过频率响应分析或瞬态响应分析求解目标结构的频域或时域响应［1-2］。星箭系统有限元模型一般规模较大，考虑到求解效率，响应分析一般采用模态法，然后通过子结构内力恢复得到结构响应和载荷［3-5］。固液捆绑火箭具有频率低、模态密、纵横扭耦合等特点，动力学特性复杂，建立能够准确反映固液捆绑火箭动力学特性的有限元模型是星箭耦合分析的关键之一。

针对以上固液捆绑火箭在动力学建模和外力函数设计中存在的问题，本文建立了典型固液捆绑火箭星箭耦合系统的纵横扭一体化有限元模型，提出基于火箭飞行特征的时域外力函数设计方法。以此为基础，针对固液捆绑火箭MDP 横向振动工况和一级关机纵向振动工况进行瞬态响应分析，通过子结构内力恢复方法，可以对星箭界面响应进行准确预示。

1 固液捆绑火箭子结构内力恢复

在外部动态载荷作用下，固液捆绑火箭结构动力学控制方程可以写为

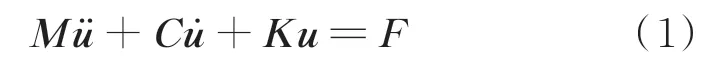
式中：M为质量阵；C为阻尼阵；K为刚度阵；F为外力向量；将物理坐标u转化到模态空间，即u=Φξ，Φ是模态向量。

利用模态向量的正交性解耦式，可以求得模态坐标ξ，进而求得u。

结构的内力Fs可以表示为［10］

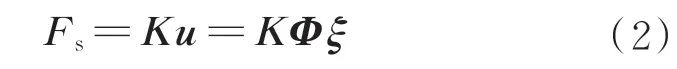
式（2）称为模态迭加法，或模态位移法。Φ采用有限阶次模态时，模态迭加法是近似的，其优势在于计算效率高。但是在纳入足够多的模态的条件下，模态迭加法也可达到较高的精度［11-12］。

在固液捆绑火箭星箭耦合分析中，使用子结构方法可以简化模型，提高计算效率。对于一个子结构，物理坐标u可以区分为界面自由度uj和内部自由度ui，则式（1）可以写为［13］

一是故意虚报盈利、高估资产信息，以达到股票上市目的。如以中核集团为例，多计利润11.07亿元，占利润总额的19.48%；2005—2009年，中核集团部分所属单位因未按规定确认未到期长期外债汇兑损益、少计收入、多计成本费用等，导致多计负债20.08亿元，少计所有者权益20.08 亿元，多计利润11.02亿元，其中2009年多计利润11.21亿元；在如兵装集团，多计利润2.95亿元，占利润总额的5.28%。2006—2009年，兵装集团本部及所属13家单位未按会计准则规定及时确认投资收益、计提坏账准备等，造成多计资产0.24亿元，少计利润5.36亿元，其中2009年少计利润2.85亿元。[2]

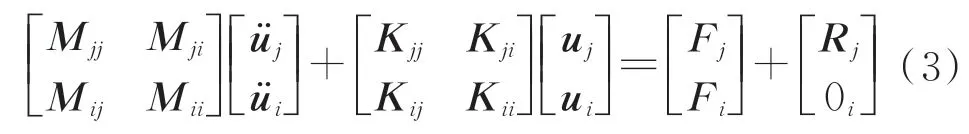
式中：下标j为界面量；下标i为内部量；Rj为界面力。

为了简略，式（3）中忽略了阻尼项，在实际星箭耦合分析计算中含有阻尼项。

将物理位移u的内部自由度转化到模态空间，即u=Φsubξ，其中

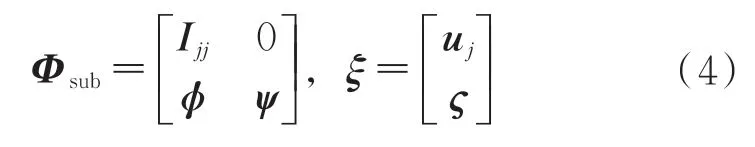
式中：ϕ的列向量分别对应着界面各个自由度的约束模态向量；ψ为子结构的界面约束模态阵；ς为内部模态坐标。

对于固液捆绑火箭，可以划分火箭子结构r 和卫星子结构s。将式（4）代入式（3），并将火箭子结构和卫星子结构组装。由于界面力协调作用，界面力Rj相互抵消，获得系统动力学方程为

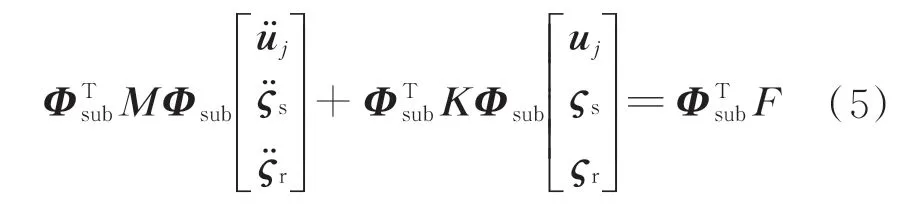
由式（5）可以求解火箭子结构r 和卫星子结构s的位移，代入式（3）可以得到火箭和卫星之间的界面力Rj。

在火箭动力学模型上施加准确的外力，通过固液捆绑火箭子结构内力恢复方法，可以获得星箭界面响应。因此，固液捆绑火箭星箭耦合分析的关键是结构动力学建模和外力函数设计。

2 固液捆绑火箭动力学建模

针对典型固液捆绑火箭（液体芯级直径3.35 m，捆绑4 台直径2.00 m 的固体助推器）开展结构动力学精细化有限元建模。固体助推器按火箭象限位置，编号为助推Ⅰ～Ⅳ。模型参考坐标系定义如下：X轴为火箭轴向，Y轴指向箭体Ⅲ象限，Z轴指向箭体Ⅳ象限，如图1 所示。

图1 典型固液捆绑火箭有限元模型Fig.1 Typical strap-on solid-liquid rocket finite element model

针对固液捆绑火箭动力学特性，建立纵横扭一体化的梁-壳组合模型。芯级纵向液体弹性特性由分块纵向质量-弹簧模型进行模拟［14-17］。整流罩用壳单元模拟，以保证该处脉动压力的响应计算准确性。捆绑连接机构由两部分组成：后捆绑位于助推器尾部，为球铰，是主传力机构；前捆绑接近助推器头锥，为三根二力杆组成的平面杆系，是辅助传力机构。后捆绑采用一个BUSH 单元模拟，前捆绑采用三个ROD 单元模拟。卫星模型采用动力缩聚模型，并应用子结构内力恢复方法求解响应和内力［18-20］。该模型能较好模拟固液捆绑火箭的低频动特性，并保证较高的计算效率。

3 基于火箭飞行特征的外力函数设计

针对固液捆绑火箭飞行试验特点，提出基于火箭飞行特征的外力函数设计方法，其主要特征为：①静动态外力函数统一在时域下给出；②控制力实时闭环反馈。平稳风、切变风、阵风引起的横向气动力大小可以通过火箭动压、攻角等飞行状态参数和平稳风、切变风、阵风风速等风场参数获得；通过设定平稳风、切变风、阵风周期，可以构造相应的时程函数。发动机推力可以基于发动机地面试车数据实测，按照工况时间截取，并进行高空推力换算。外力函数设计过程中，主要难点是脉动压力时程函数设计以及控制力反馈设计，以下对这两项分别进行说明。

3.1 脉动压力时程函数设计

脉动压力是火箭跨声速飞行时在整流罩等变截面位置产生的压力波动，本文基于脉动压力地面风洞试验构造脉动压力时程，如图2 所示。火箭设计阶段，需要基于缩比模型进行脉动压力地面风洞试验，试验测得脉动压力激励截面两个正交方向的截面合成脉动压力时程数据。这一时程数据经过缩比模型试验状态和实际火箭飞行状态的时间相似变换，即可得到飞行工况下的脉动压力时程数据。时间相似变换如下：

图2 典型截面脉动压力时程Fig.2 Typical section buffet force in time domain

式中：T为时间；D为截面直径；V为速度；下标m 为缩比模型风洞试验中的参数；下标f 为实际飞行状态中的参数。

在耦合分析中，截取同一时段两个正交方向的时程数据作为脉动压力施加，即可以保留正交方向脉动压力数据之间的时间相关性。需要注意由于存在时域上的截断，获得的脉动压力时程数据的功率谱与脉动压力试验平均功率谱一般存在差异，需进行一定修正，以防止时域截断引起的随机性影响星箭耦合分析结果。

3.2 固液捆绑火箭控制力反馈设计

火箭在飞行过程中，通过惯组、陀螺等敏感元件获得自身的运动信息，并通过控制系统反馈给发动机使发动机摆动，产生横向的控制力。控制系统的仿真可通过在MSC.Nastran 平台中应用控制系统传递函数实现。其反馈过程为：从模型对应位置获得姿态角、角速度等运动信息，经过控制系统的传递函数，获得反馈的固、液发动机摆角，并转化为控制力施加于发动机处，反馈过程如图3 所示。典型固液捆绑火箭MDP 工况中，在外力作用下，经过控制系统反馈得到的固、液发动机摆角时程如图4所示。

图3 控制系统反馈回路Fig.3 Closed-loop feedback of the control system

图4 固、液发动机经过控制系统反馈得到的摆角Fig.4 Swing angle output of the solid and liquid engine feedback by the control system

4 固液捆绑火箭星箭耦合分析

基于上述固液捆绑火箭星箭耦合系统有限元模型以及外力函数，进行瞬态响应分析，通过子结构内力恢复对火箭典型工况MDP 工况和一级关机工况的星箭界面总时域加速度响应进行预示，并依据获得的星箭界面总加速度时域响应，计算星箭界面冲击响应谱（Shock Response Spectrum，SRS），本文取品质因子Q=10。

4.1 MDP 工况

火箭MDP 工况的星箭界面响应最大值预示结果见表1。星箭界面加速度时域结果和SRS 如图5 所示。从分析结果来看，该工况SRS 最大横向响应为0.6 g 量级，在4、10、16、25 Hz 附近出现峰值，其来源主要是横向外力输入与星箭组合体在对应频率产生耦合，产生较大的横向响应。

表1 MDP 工况星箭界面SRS 最大响应Tab.1 Maximum SRS response of the satellite-launch vehicle interface under the MDP working condition

图5 MDP 工况星箭界面时域响应和SRSFig.5 Response of the satellite-launch vehicle interface in time domain and SRS under the MDP working condition

4.2 一级关机工况

火箭一级关机工况的星箭界面响应最大值预示结果见表2。星箭界面加速度时域结果和SRS 如图6 所示。从分析结果来看，该工况SRS 最大纵向响应为0.4g量级，在16、30 Hz 附近出现峰值，其来源主要是发动机关机过程推力下降引起的冲击与星箭组合体在对应频率产生耦合，产生较大的纵向响应。

图6 一级关机工况星箭界面时域响应和SRSFig.6 Response of the satellite-launch vehicle interface and SRS under the first stage shutdown working condition

表2 一级关机工况星箭界面SRS 最大响应Tab.2 Maximum SRS response of the satellite-launch vehicle interface under the first stage shutdown working condition

5 结束语

针对固液捆绑火箭星箭耦合分析在结构动力学建模和外力函数设计中存在的技术难点，建立了纵横扭一体化星箭耦合系统有限元模型，提出基于火箭飞行特征的外力函数设计方法。对星箭耦合系统进行瞬态响应分析，并通过子结构内力恢复，对固液捆绑火箭MDP、一级关机等典型工况星箭界面低频振动力学环境进行准确预示。本文提出的星箭耦合分析方法具有较高的工程应用价值，该方法在后续研究中通过进一步提升动力学建模精细度，还可以应用于火箭特定位置的力学环境预示。