分裂四元数矩阵方程AXB+CY D =E 的最小二乘η-埃尔米特解问题

张 颖, 王伟华, 魏佳宁, 张会生

(大连海事大学理学院，大连 116026)

0 引言

矩阵方程是矩阵理论的一个重要研究领域，约束矩阵方程问题就是在满足一定约束条件的矩阵集合中求矩阵方程解的问题。不同的论域、不同的约束条件、不同的矩阵方程类型导致了不同的约束矩阵方程问题，约束类矩阵方程问题在很多领域有着广泛应用。例如，有限元静态模型修正问题能归结于矩阵方程AX=B求约束解问题。不同研究领域的各类问题推动了约束矩阵方程理论的发展。

分裂四元数及其矩阵理论在数学研究和物理应用中占重要角色。例如，Kula 和Yayli[1]利用分裂四元数表示半欧空间的运动，并将分裂四元数按类空、类时、类光进行分类。随后，¨Ozdemir 等[2]利用类时分裂四元数表示三维Minkowski 空间中的洛伦兹变换和旋转变换；Yormaz 等[3]指出分裂四元数及其矩阵能被用于刚体力学中的势能哈密顿方程中。量子力学理论涉及许多数学物理模型，这些模型的研究可以转化成对分裂四元数矩阵方程的研究。此外，在理论研究和数值计算中，为了解决如摄动理论，薛定谔方程和Riccati 方程，有时也需要解决分裂四元数矩阵方程。分裂四元数矩阵方程不仅有着广泛的物理背景，而且对矩阵论本身也是有益补充，因而对分裂四元数矩阵方程进行研究具有重要意义。当前，分裂四元数矩阵方程如AX=B[4]、AX+XB=C[5]、AXAH+BY BH=C[6]、AX*-XB=CY+D、X-AX*B=CY+D[7]以及AXB+CXD=E[8]已经得到了广泛研究。然而，就前面提到的分裂四元数上的求解问题，仍亟待进一步的研究与发现。

对于一般矩阵方程AXB+CY D=E，现阶段已经取得了丰富的研究成果[9–16]，然而这些成果都是基于实数域讨论的。Yuan 等[17]将这个一般方程的研究推广到四元数上，利用最小范数推导了最小二乘解。随后，研究了矩阵方程AHXA+BHY B=C的最小二乘η-埃尔米特解[18]，η-埃尔米特矩阵常常出现在宽线性模型处理中[19]。由于η-埃尔米特矩阵具有Autonne-Takagi 分解[20]，这一分解可以有助于进行数学和物理问题的研究。然而，目前对分裂四元数矩阵方程AXB+CY D=E的约束解问题的研究少有报道，尤其是η-埃尔米特解，对这一问题的研究是非常有意义的。

1849 年，James Cockle 提出了分裂四元数，分裂四元数集合表示如下

其中i2=-1,j2=k2=1,ijk=1 以及ij=-ji=k,jk=-kj=-i,ki=-ik=j。分裂四元数q的共轭q*=qa-qbi-qcj-qdk，其满足(pq)*=q*p*。分裂四元数的范数

这里Iq=qq*。若Iq/=0，则

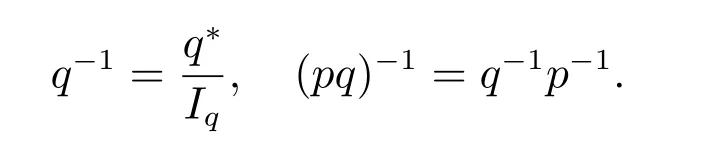
为便于本文研究，现引入分裂四元数对合和反对合变换。我们称满足以下公理的变换x →f(x)表示对合运算(或反对合运算)[21]。

公理1反身性：f(f(x))=x。

公理2线性性：f(x1+x2)=f(x1)+f(x2),λf(x)=f(λx)，其中λ是实常数。

公理3反序性：f(x1x2)=f(x2)f(x1)。

反对合运算类似对合运算，仍是自反变换。除不满足公理3 外，还需满足以下公理。

公理4正序性：f(x1x2)=f(x1)f(x2)。

定义1对任意分裂四元数q ∈QS，定义如下变换

特别地，如果式(2)中的μ是纯单位四元数(没有实部)，则式(2)即为四元数反对合变换，例如，qi、qj和qk可定义为

对于任意分裂四元数矩阵A=A1+A2j ∈QSm×n，其中A1,A2∈Cm×n。AT、¯A以及AH分别表示分裂四元数域上的转置，共轭以及共轭转置运算。A的复值表示矩阵形式定义如下[8]

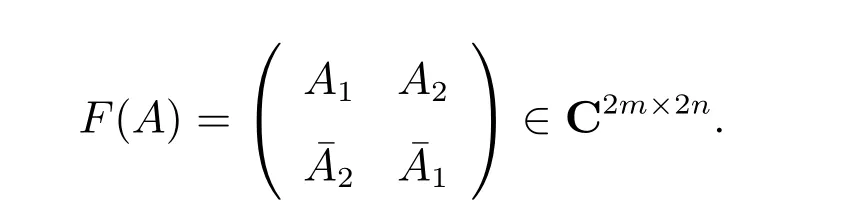
记ΦA=(A1,A2),(ReA1,ImA1,ReA2,ImA2)。令av=(a1v,a2v,···,amv)(v=1,2,···,n)，则矩阵A的拉直运算vec(A)可定义为

vec(A)=(a1,a2,···,an)T.

定义2[18]如果矩阵A ∈QSn×n满足AηH=A，则称A为η-埃尔米特矩阵；反之，如果满足AηH=-A，则称A为η-反埃尔米特矩阵，其中η ∈{i,j,k}。η-埃尔米特矩阵集合和η-反埃尔米特矩阵集合分别记为ηHQSn×n和ηAQSn×n。

在文献[8]中，Yuan 等指出对于A=(auv)∈QSm×n以及

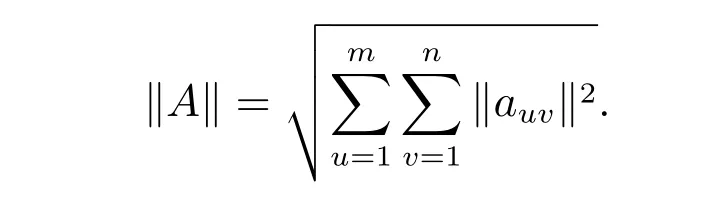
由于‖A‖/=‖ΦA‖，这使得分裂四元数矩阵方程求解最小二乘解非常困难。值得注意的是，Zhang 等[4]通过分裂四元数矩阵的复表示研究了分裂四元数最小二乘问题。一个分裂四元数矩阵的Frobenius 范数可用以下Frobenius 范数(或Euclid 范数)表示，即

‖A‖F=‖F(A)‖F,

则

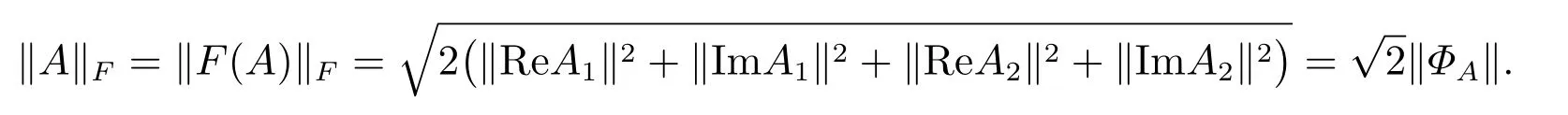
在前面工作的基础上，利用处理最小二乘问题[8]和η-埃尔米特矩阵问题[4]的现有方法，通过引入分裂四元数矩阵的Frobenius 范数，这个范数是基于分裂四元数矩阵的复表示定义的，本文研究了分裂四元数矩阵方程AXB+CY D=E的最小二乘问题。

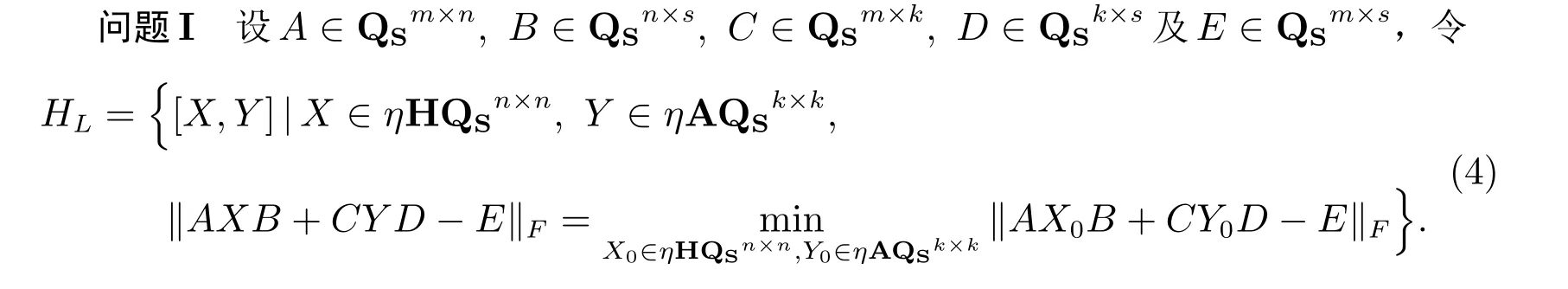
寻找[XH,YH]∈HL，使得

在下面的讨论中，首先给出预备引理，其次推导问题I 的求解表达式，最后举例验证求解表达式的可行性。

1 预备引理

为了研究问题I 的解，我们首先引入ηHQSn×n和ηAQSn×n的结构，并且给出一些预备引理。

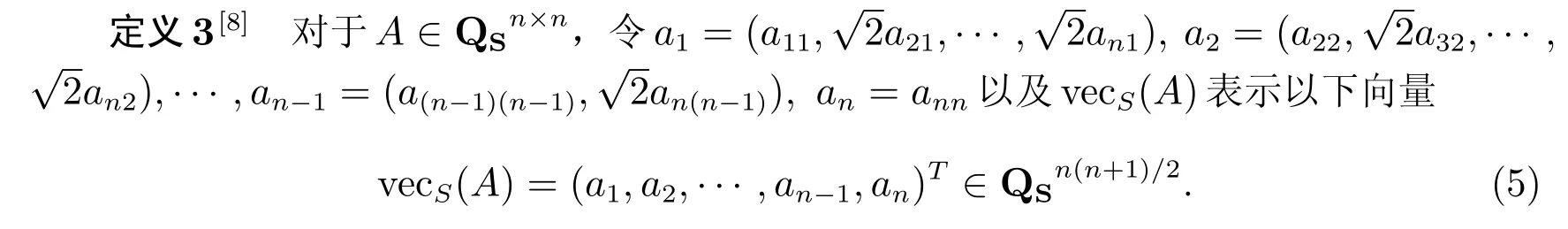
定义4[8]对于B ∈QSn×n，令b1= (b21,b31,···,bn1),b2= (b32,b42,···,bn2),···,bn-2=(b(n-1)(n-2),bn(n-2)),bn-1=bn(n-1)以及vecA(B)表示以下向量

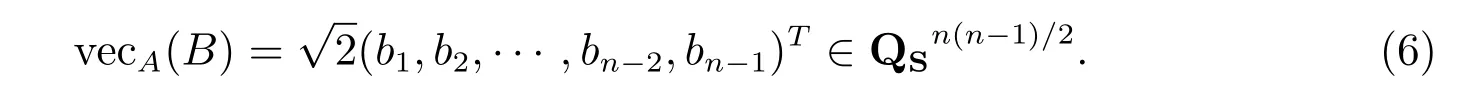
引理1[8]设X ∈Rn×n，则

X是对称矩阵⇔vec(X)=KSvecS(X),

其中KS ∈Rn2×n(n+1)/2具有以下形式

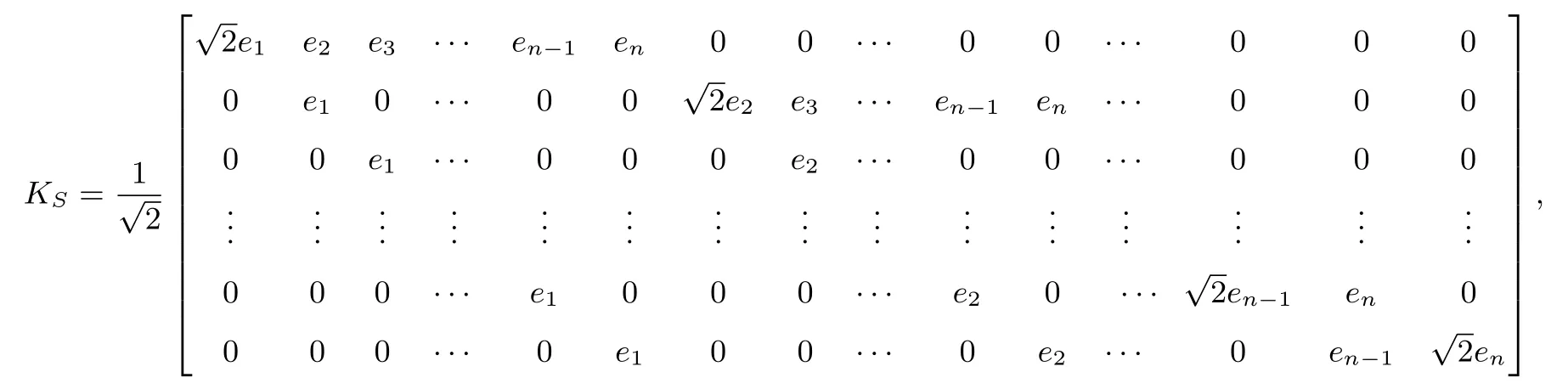
这里ei是单位矩阵In的第i列。另外

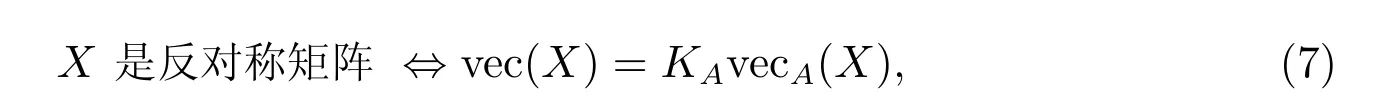
其中KA ∈Rn2×n(n-1)/2具有以下形式

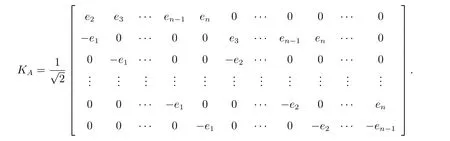
类似[8,22]，我们能得到分裂四元数的以下引理。

引理2如果X=X1+X2j ∈QSn×n，则

其中

引理3如果Y=Y1+Y2j ∈QSk×k，则

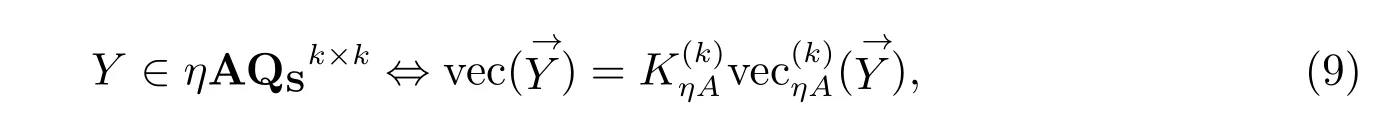
其中

引理4[8]令A=A1+A2j ∈QSm×n,B=B1+B2j ∈QSn×s和C=C1+C2j ∈QSs×t，那么

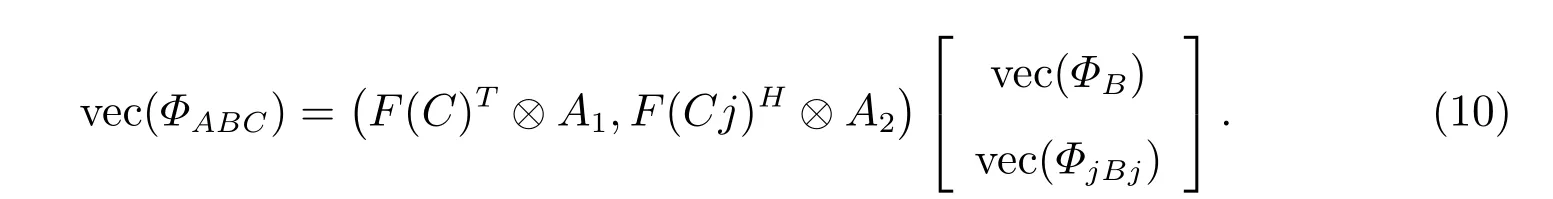
记

则vec(ΦAXB)和vec(ΦCY D)能进行如下表示。

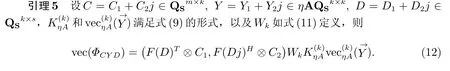
证明 对于Y=Y1+Y2j ∈ηAQSk×k，由式(9)可知

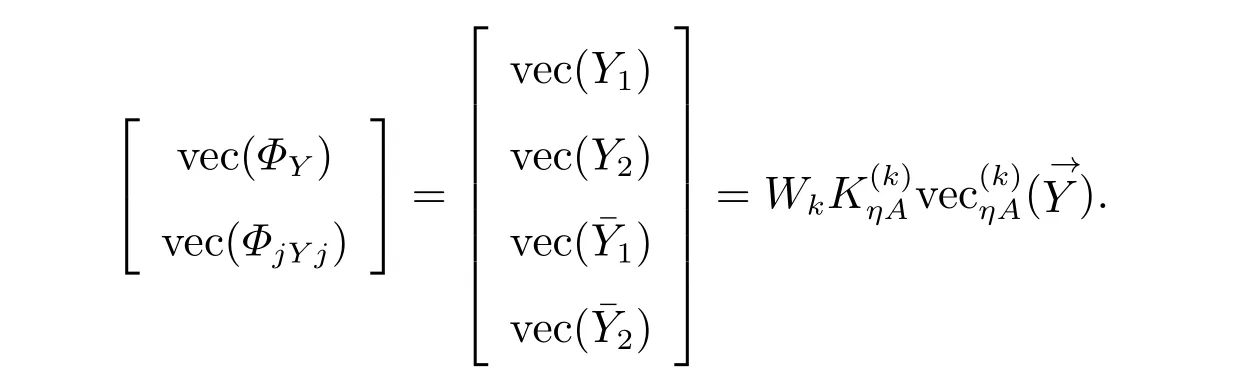
再根据式(10)，我们能得到式(12)。

引理7[23]对于A ∈Rm×n和b ∈Rn，矩阵方程Ax=b有解x ∈Rn，当且仅当

AA+b=b.

此时，通解为

x=A+b+(I-A+A)y,

其中y ∈Rn是任意向量。

引理8[23]对于A ∈Rm×n和b ∈Rn，矩阵方程Ax=b的最小二乘解能表示成

x=A+b+(I-A+A)y,

其中y ∈Rn是任意向量，且极小范数最小二乘解是x=A+b。

2 问题I 求解

对于A=A1+A2j ∈QSm×n,B ∈QSn×s,C=C1+C2j ∈QSm×k,D ∈QSk×s,E ∈QSm×s，设

以及

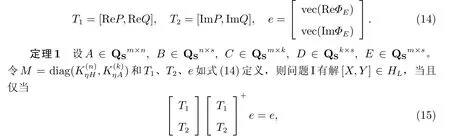
上述条件成立，则有其中z ∈R2n2+n+2k2-k是任意向量。

进一步，如果式(15)成立，则分裂四元数矩阵方程(4)有唯一解[X,Y]∈HL，当且仅当

此时

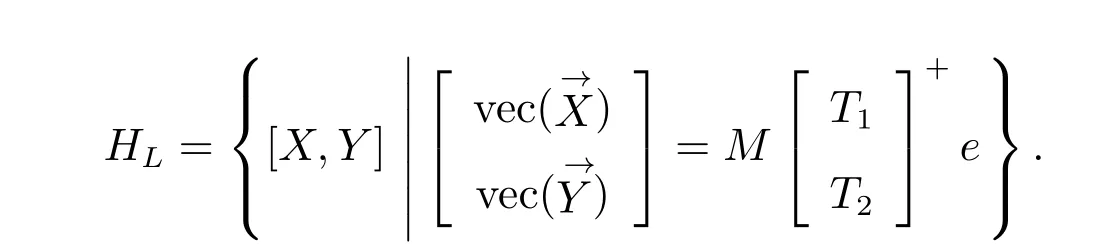
证明 由引理5 和引理6，可得

再由于引理7 和引理8，有

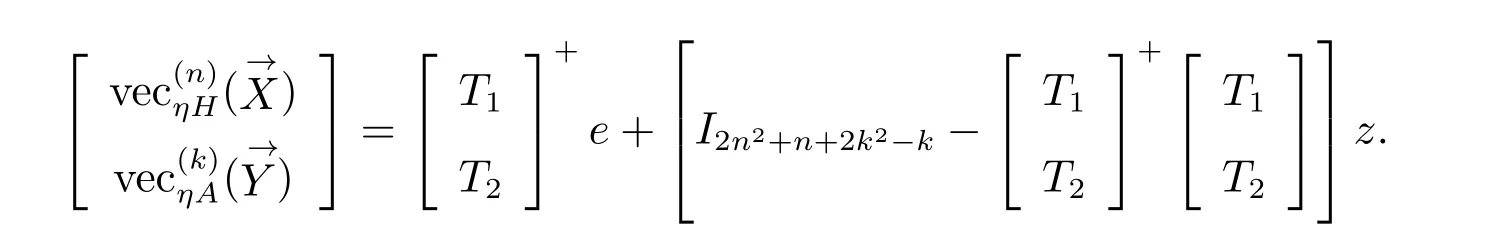
因此

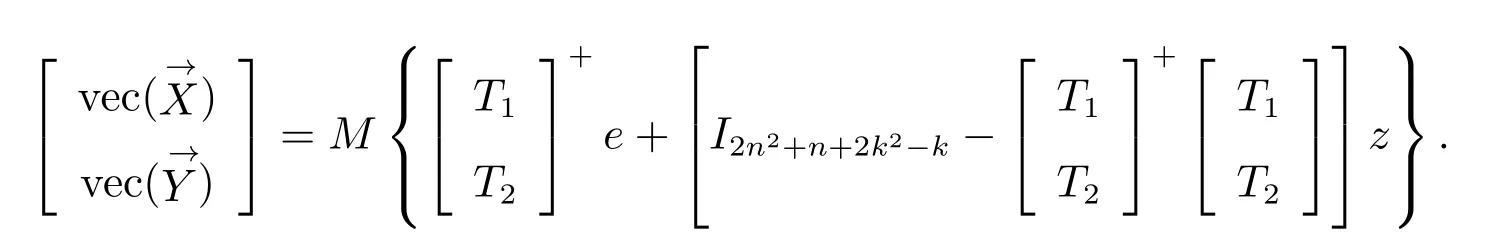
3 举例

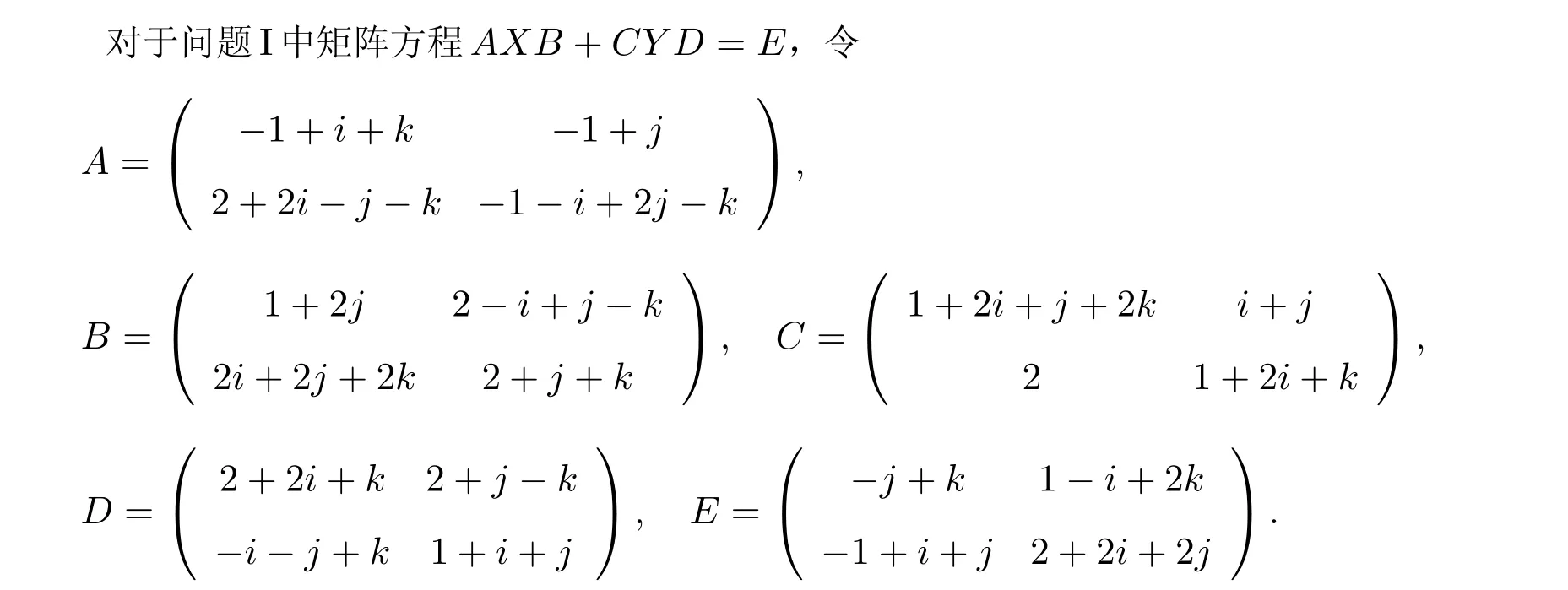
对于不同的η(η=i,j,k)，我们分别讨论问题I。

我们能得到一组解[X,Y]，其中

数值实验表明，式(15)仍以误差10-13成立，所以问题I 有解。对上述z，我们能得到一组解[X,Y]，其中

数值实验以误差10-13，式(15)成立，所以问题I 有解。对上述z，我们能得到一组解[X,Y]，其中

需要指出的是，上面三种情形，式(16)也成立，所以上述解[X,Y]也是唯一的极小范数解(在Frobenium 范数)。这个例子验证了求解表达式的可行性。

4 小结

分裂四元数中‖A‖/=‖ΦA‖，这使得分裂四元数矩阵方程求解最小二乘解非常困难。本文通过引入分裂四元数矩阵的Frobenius 范数，这个范数是基于分裂四元数矩阵的复表示定义的，并利用矩阵的Moore-Penrose 广义逆以及Kronecker 积，推导了分裂四元数矩阵方程AXB+CY D=E的最小二乘η-埃尔米特解以及唯一的极小范数解的表达式，数值算例验证了表达式的可行性。