任意多边形上非定常扩散方程的单元中心型有限体积格式

单 丽, 金 珠, 张海成

(1. 汕头大学理学院，汕头 515063; 2. 辽宁工程技术大学理学院，阜新 123000;3. 华东师范大学数学科学学院，上海 200241)

0 引言

扩散问题在辐射流体力学、辐射磁流体力学和油藏的数值模拟中有着广泛应用，直接在非光滑、扭曲严重的多边形网格上构造扩散问题的高精度计算格式具有非常重要的研究意义。有限体积法适用于结构和非结构网格，因其保持数值通量的局部守恒性、计算量足够小、易于编程等优点，被广泛应用于诸多实际问题的数值模拟。近年来，科研工作者提出了扩散方程的多种有限体积格式，如九点格式[1]、多点流逼近格式[2–3]、节点控制体格式[4]、支撑算子格式[5–6]等，按照未知量的类型，大致分为单元中心型格式、网格节点型格式和杂交格式等。

文献[7–8]基于线性精确准则，构造了一个在扭曲网格上求解扩散方程的九点格式。所谓线性精确是指当解析解是关于自变量的线性函数且扩散系数是常数时，每一个离散步骤都是精确成立的。该格式首先利用网格节点未知量和网格中心未知量离散扩散算子，然后将网格节点未知量用其周围网格单元中心未知量的加权均值进行替换，最终构造出单元中心型离散格式。对于四边形网格，他们采用的加权方式共三种，分别是取网格节点周围四个网格单元中心量算数平均插值、逆距离加权插值和双线性插值。前两种加权方法不满足线性精确性质，第三种满足，但却只局限于应用四边形网格。本文将网格节点周边的单元中心未知量分别在该网格节点处进行Taylor 展开，通过求解一个欠定方程确定权重，进而提出一种新的单元中心型有限体积格式，该格式既满足线性精确性质，又可以在任意多边形网格上应用。

本文针对非定常扩散方程，时间采用向后欧拉进行离散，空间上采用新的有限体积格式进行离散，分别与文献[7]中提出的三种加权方式得到的有限体积格式比较，在随机四边形网格、Shestakov 网格、锐角三角形网格和多边形网格上进行数值实验。数值结果表明，新格式在保证接近二阶收敛精度的前提下，收敛速度相比其他三种格式都有提升，计算精度稳定。本文的结构如下：第1 节具体介绍多边形网格上的有限体积格式构造；第2 节通过数值算例来验证格式的精度和可行性；第3 节给出本文的结论。

1 多边形网格上的有限体积格式

考虑如下非定常扩散方程

其中Ω ⊂R2为平面上有界单连通多边形区域，λ ＞0 是非定常扩散方程的系数，f ∈L2(Ω)为源项，g是在∂Ω上给定的适定光滑的函数。

假设将区域Ω被剖分为有限个互不重叠的多边形网格单元C={A,B,C,D,···}，且任意两个多边形单元至多有一条公共边或者一个公共顶点。令ε表示所有网格边组成的集合，εint=ε ∩Ω表示所有不位于区域边界上的网格边所组成的集合，εext=ε ∩∂Ω表示所有位于区域边界上的网格边组成的集合。网格单元A的几何中心为OA，其坐标为(xA,yA)，符号SA为单元A的面积。同时，将时间区间[0,T]等分成N份，每个时间结点记为t0,t1,t2,...,tN，记时间步长Δt=，简记u=u(xA,yA,tn+1)。

本文中以线性精确准则作为离散格式的出发点，即，当控制方程(1)的解析解u(x,y,t)是关于自变量的线性函数，并且扩散系数λ(x,y,t)是常数时，每一个离散步骤都是精确成立，符号≃表示此线性精确意义下的相等。

记F=-λ(x,y,t)∇u表示热流，则非定常扩散方程(1)等价于

在t=tn+1时刻，将热传导方程(4)在网格单元A上进行积分，∂A表示网格单元A的所有边，nA,σ表示单元A的一条边σ上的单位外法向量。由高斯散度定理得

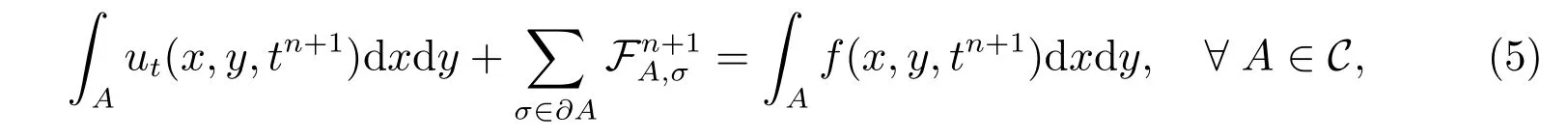
其中网格边σ上的法向流通量F定义如下

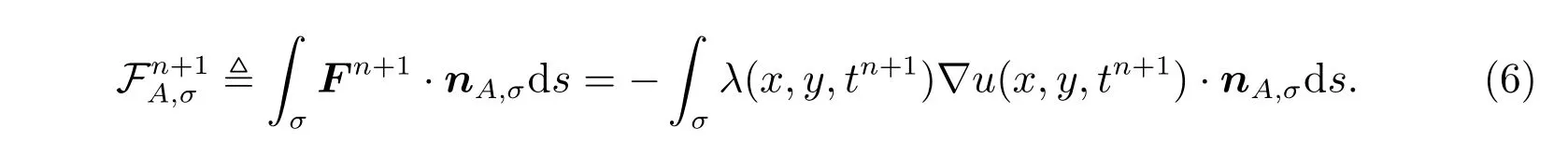
值得注意的是，如果边σ是两个网格单元A和B的公共边，则有如下局部守恒方程

利用该网格中心值离散(5)式中的右端源项，左端的时间导数项在(tn,tn+1)上采用向后欧拉格式进行离散，得到如下非定常扩散方程的有限体积格式

其中U=U(xA,yA,tn+1)表示未知量u在网格单元A的中心点OA处，tn+1时刻的数值解，F表示网格边法向流F的近似。一旦确定了法向流的近似表达式，有限体积格式就构造完成。下面详细推导F的近似表达式，这也是有限体积格式构造的核心。以网格单元A为例，假设它的一条边为σ=PQ，P点坐标为(xP,yP)，Q点坐标为(xQ,yQ)，其中心OA到边PQ的距离记为hA。若存在一个单元B与单元A共用边PQ，则单元B的中心OB到边PQ的距离记为hB，如图1 所示。

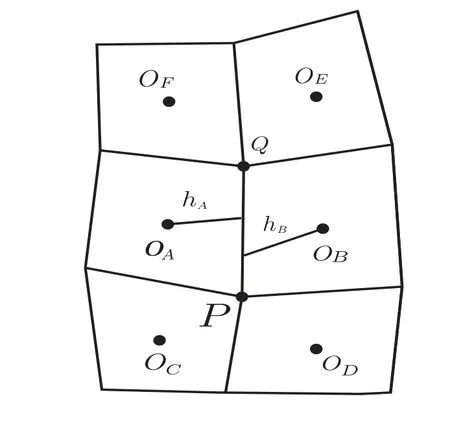
图1 网格单元A 及其相邻单元

其中

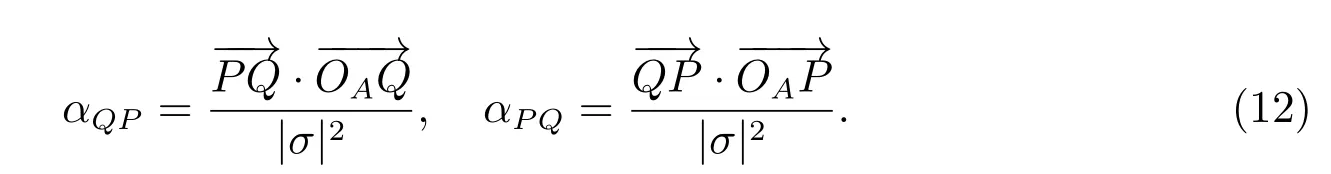
显然αQP+αP Q=1。将(11)式代入法向流的定义中，有

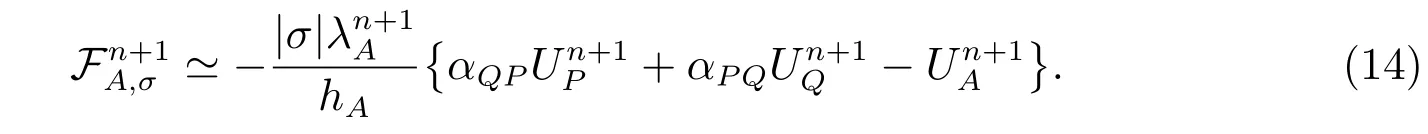
若边σ对侧存在单元B，则在三角形形△OBQP上，可用相同方法得到

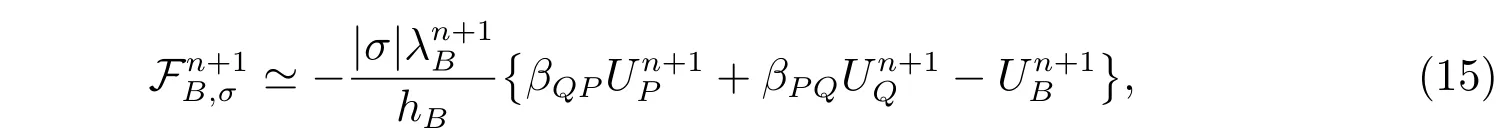
其中

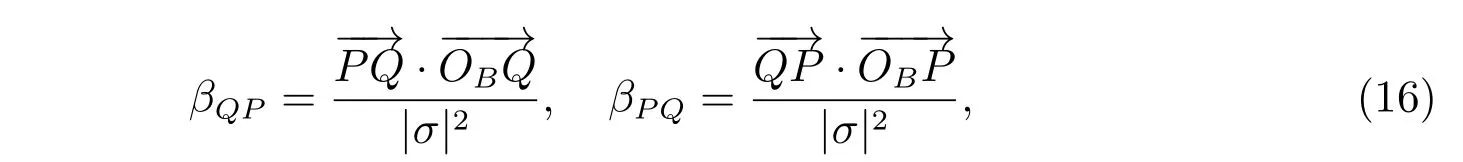
且满足βQP+βP Q=1。利用(7)式给出的局部守恒性条件，将(14)式和(15)式求和，可得到法向流的双侧逼近为

其中

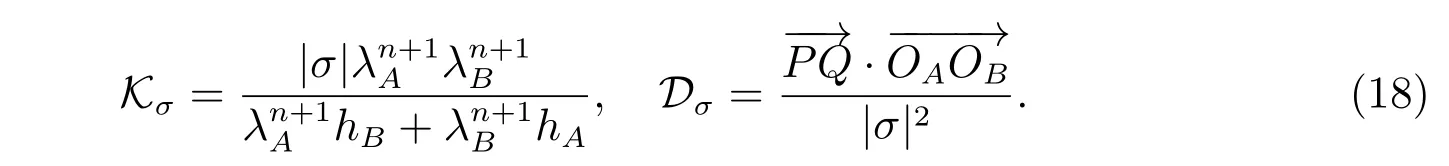
综上，对于边界网格边F采用(14)式给出的逼近公式，对于内部网格边，采用(17)式给出的逼近公式。

将上述法向流的逼近表达式(14)或者(17)式代入(8)式中，发现格式中同时出现了网格中心点的未知量U和网格节点处的未知量U、U，如果该网格节点在网格边界上，则直接用边界条件赋值，否则该网格节点处的未知量通常是利用其邻近网格中心处的未知量的某种加权均值进行替换，最终构造出只含有网格单元中心处未知量信息的单元中心型有限体积格式。

对于四边形网格而言，假设P为网格单元节点，OA、OB、OC、OD为以节点P为公共交点的四个网格单元的中心点，如图2 所示，韩昌昊等[8]给出了如下三种加权方式。

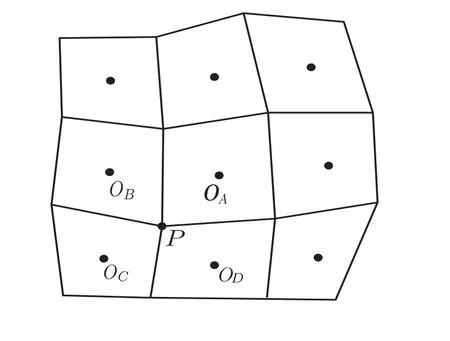
图2 九点格式模板

第一种：算数加权平均

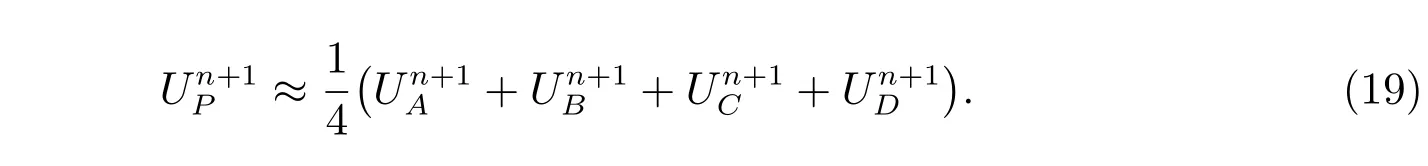
第二种：逆距离加权平均

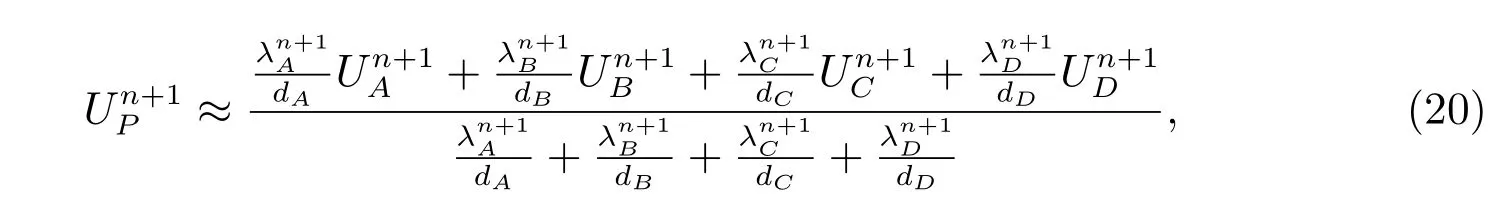
其中di(i=A,B,C,D)表示网格节点P到四个网格中心点的距离，这两种加权方式也适用于任意多边形网格，权重根据P点周围的单元个数进行相应的调整即可，但是不难验证这两种加权方式是不满足线性精确准则的。

第三种：利用四个相邻网格中心未知量的双线性插值来近似网格节点未知量，即

其中ζ、η由如下二次方程组确定

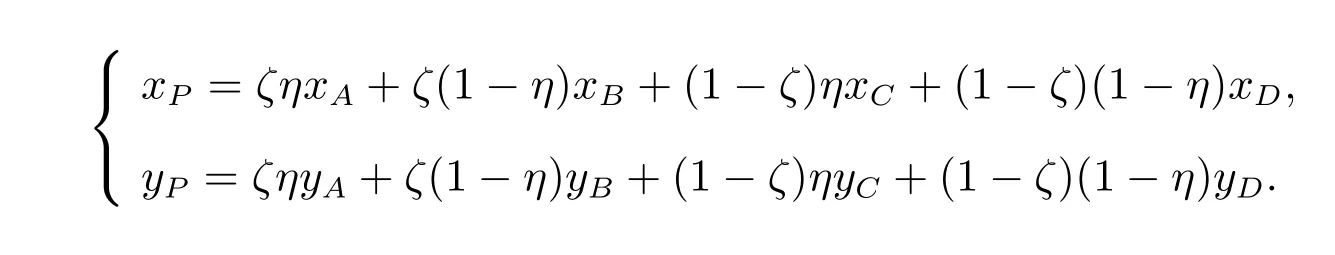
该加权方式满足线性精确准则，但缺点在于只适用于四边形网格，不能推广到任意多边形网格。

为了构造能够适用于任意网格的满足线性精确准则的有限体积格式，本文提出第四种加权方式。以三角形网格为例，假设内部网格节点P周围有五个单元，如图3 所示，将周围五个单元中心处的函数值在该点做Taylor 展开得

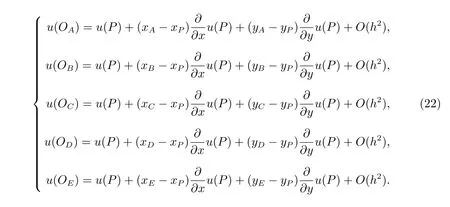
图3 消除辅助插值点

将(22)式的五个等式分别乘以系数ωA、ωB、ωC、ωD和ωE并相加，发现当这五个系数满足欠定线性方程组

时，就可以得到如下线性精确的加权方式

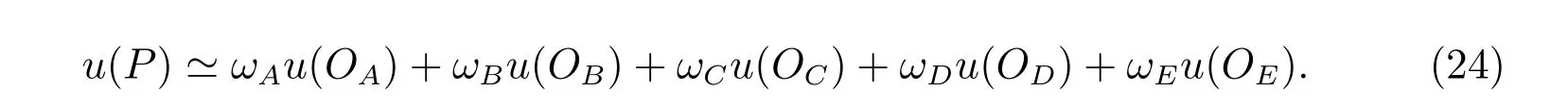
欠定方程组(23)的矩阵形式为

其中

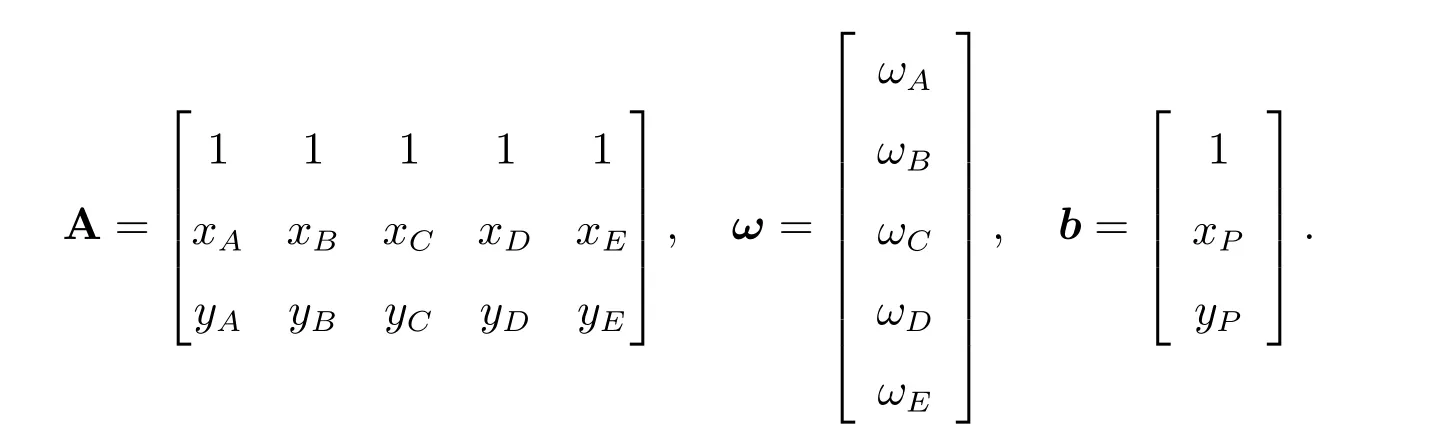
令

则(25)式等价于方程组

先求解适定方程组(27)的解ω′，再将其代入(26)式中，就能得到系数ω。于是第四种加权公式为

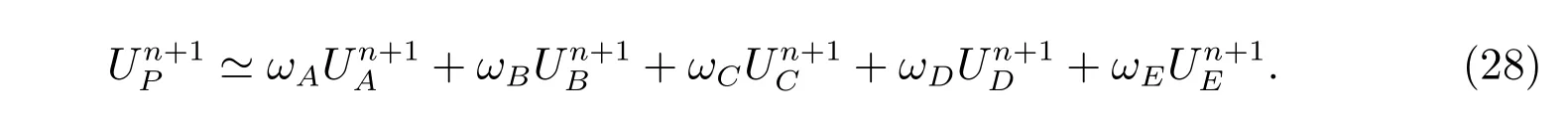
运用同样的方法可以得到U的加权公式，将它们代入(17)式，进而代入(8)式中，即可得到只含单元中心未知量的有限体积格式。

2 数值算例

为了测试新格式的精度，在物理区域Ω= [0,1]×[0,1]上，分别采用锐角三角形网格、随机四边形网格、多边形网格和Shestakov 网格[9]，如图4 至图7 所示，每类网格都有4 个不同的尺寸。考察如下定义的L2误差

图4 随机四边形网格(p=0.4)

图5 Shestakov 网格(p=0.35)

图6 锐角三角形网格

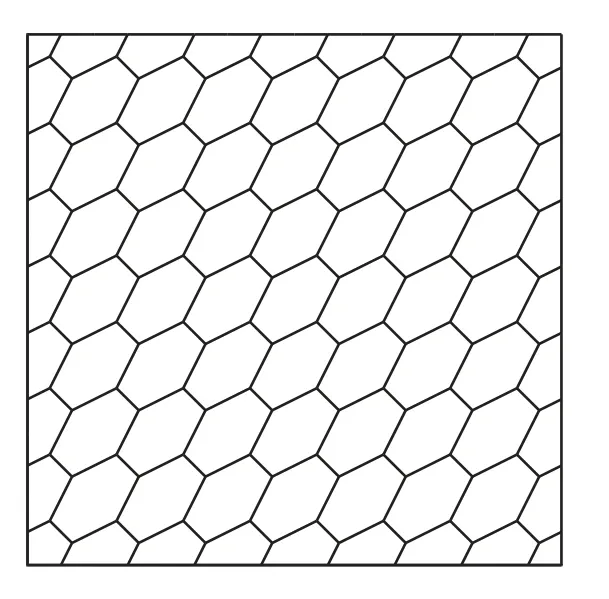
图7 多边形网格

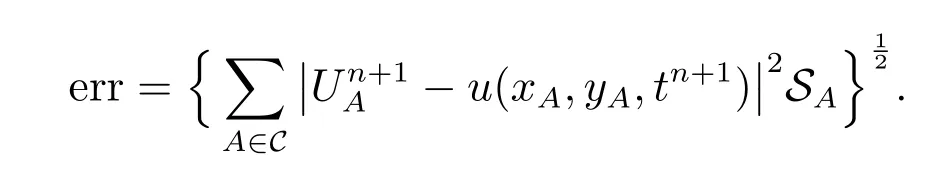
对尺寸分别为h1、h2的网格，收敛阶order 按照下面公式计算

随机四边形网格节点由一组均匀分布的节点按如下公式做随机扰动产生

其中r1,r2∈[0,1]是两个相互独立的随机产生的随机数，p ∈[0,0.5]反映随机四边形网格扭曲程度，若p值取的越大，说明随机四边形网格越扭曲，但网格不会出现重叠的现象。本文的扭曲程度参数p取为0.4。

为了对比不同加权方式的优劣性，我们用NPS1、NPS2 分别表示按算数加权平均(19)式和逆距离加权平均(20)式选择加权系数，LES1 表示按双线性插值(21)式进行加权，LES2 表示按新的加权方式(28)式选取的加权系数。我们首先考虑扩散系数是连续的情形，其中算例1 为扩散系数为常数的情形，算例2 为扩散系数为张量的情形。其次，我们在算例3 考虑扩散系数是间断的情形。算例4 考虑扩散系数是常数，同时解析解是线性函数的情形。算例5 考虑扩散系数依赖未知量的非线性扩散方程的情形。

算例1(扩散系数是连续常数) 在单位正方形区域[0,1]×[0,1]上，考虑如下非定常扩散方程

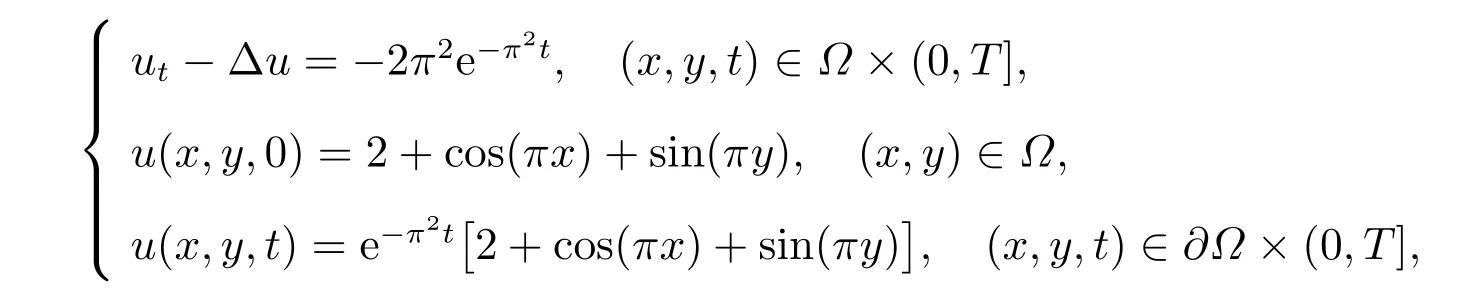
其精确解为

u(x,y,t)=e-π2t[2+cos(πx)+sin(πy)].

在随机四边形网格和Shestakov 网格上，时间步长取为Δt=，表1 和表2 分别列出了在T= 0.1 时刻，四种算法的计算结果。不难发现，LES1 和LES2 都达到了二阶收敛速度，而NPS1 和NPS2 无法达到。在锐角三角形网格和多边形网格上，时间步长取Δt=h2，其中h表示三角形单元中和多边形单元中边长的最大值，表3 和表4 列出了在T= 0.1 时刻，NPS1、NPS2 和LES2 的计算结果。LES2 算法依然可以达到二阶收敛，计算精度和收敛阶都优于NPS1 和NPS2。

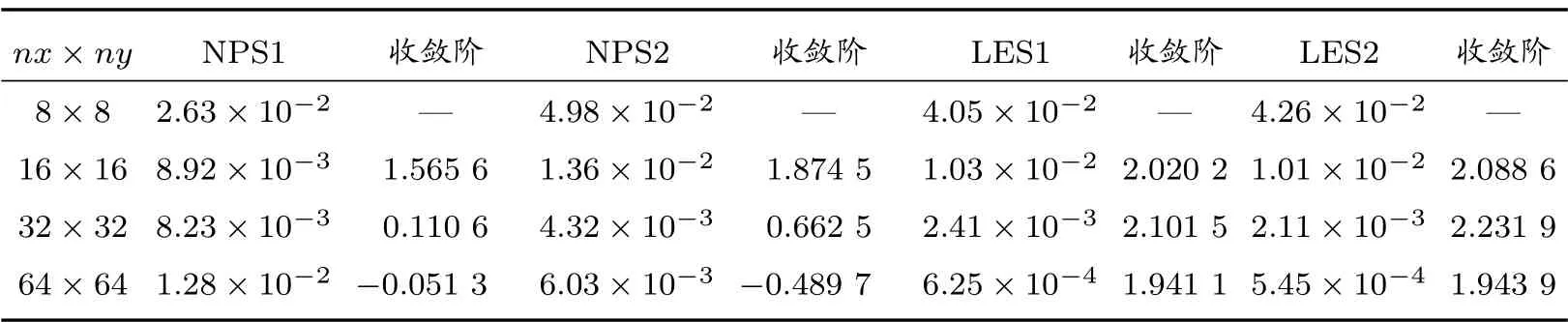
表1 算例1 在随机四边形网格上的L2 误差及收敛阶

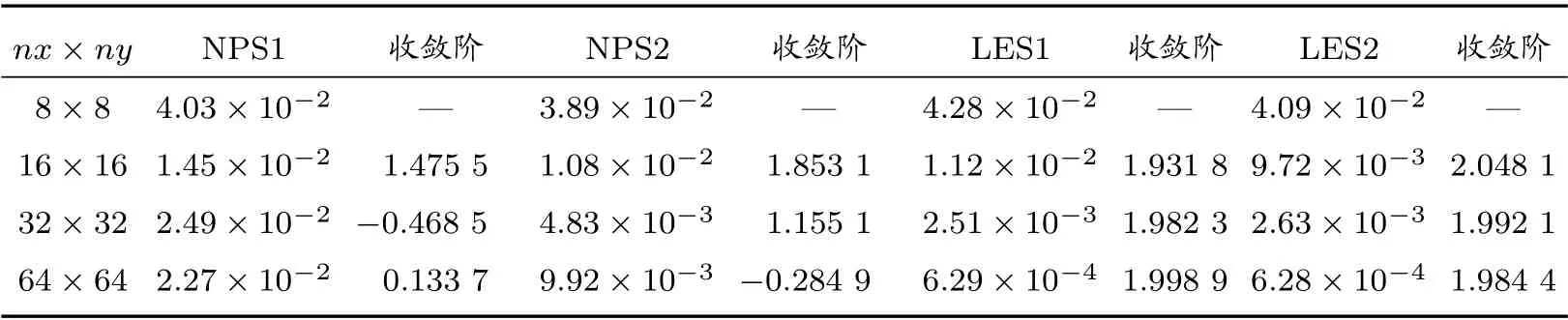
表2 算例1 在Shestakov 网格上的L2 误差及收敛阶

表3 算例1 在锐角三角形网格上的L2 误差及收敛阶

表4 算例1 在多边形网格上的L2 误差及收敛阶

算例2(扩散系数是连续张量) 在单位正方形区域[0,1]×[0,1]上，考虑如下非定常扩散方程

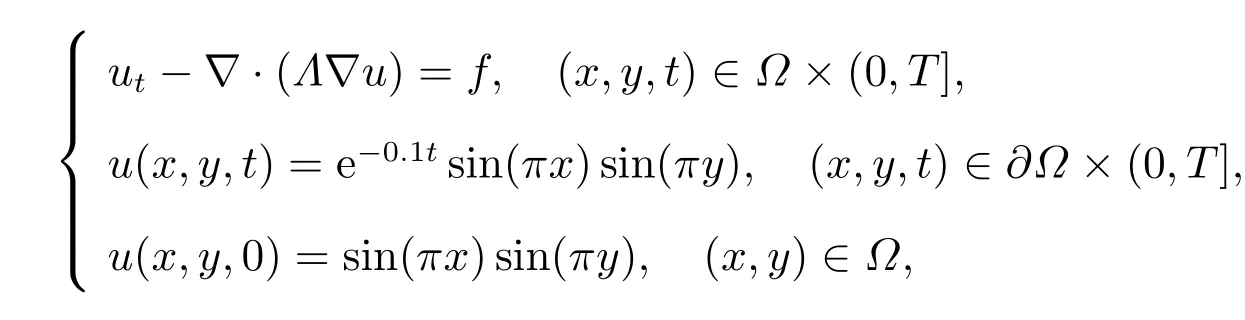
其中Λ是一个对称正定矩阵，Λ=RDRT，而

这里取

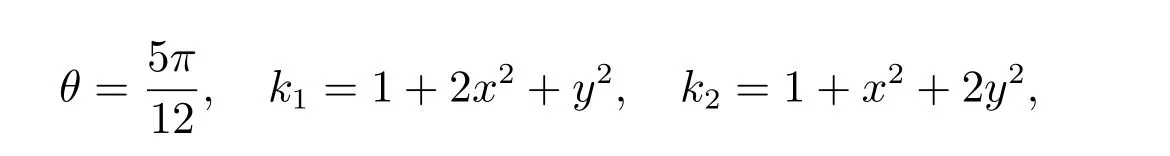
其精确解为

u(x,y,t)=e-0.1tsin(πx)sin(πy).

表5 和表6 分别列出了在T= 0.001 时刻四种算法在随机四边形网格和Shestakov 网格上的计算结果，不难发现LES1 算法和LES2 算法依然可以达到了二阶收敛速度，而NPS1 和NPS2 算法不能。同样，表7 和表8 给出了在锐角三角形网格和多边形网格上的计算结果，时间步长Δt的选取同算例1，LES2 算法依然可以达到二阶收敛，计算精度和收敛阶都优于NPS1 和NPS2。

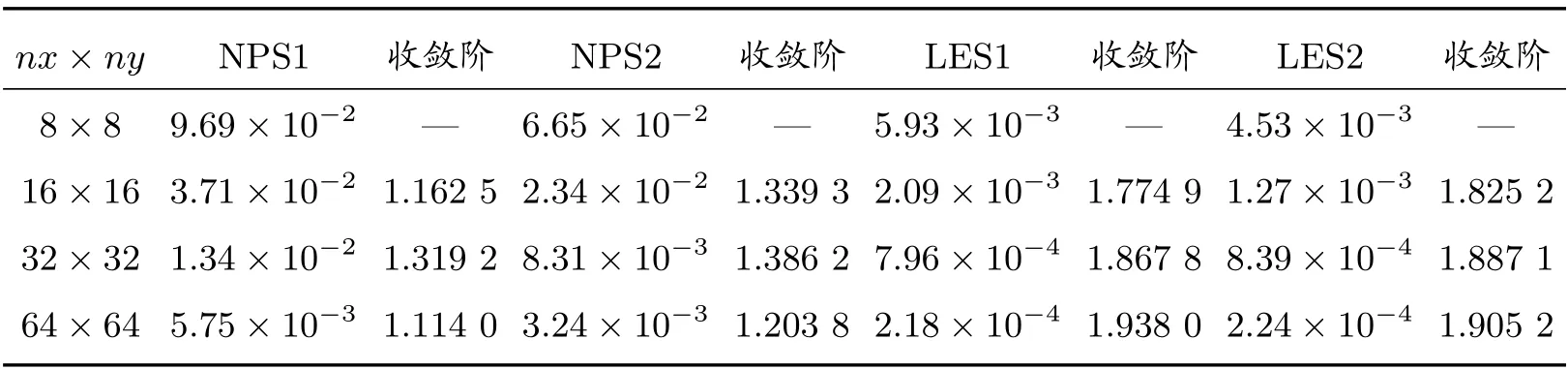
表5 算例2 在随机四边形网格上的L2 误差及收敛阶

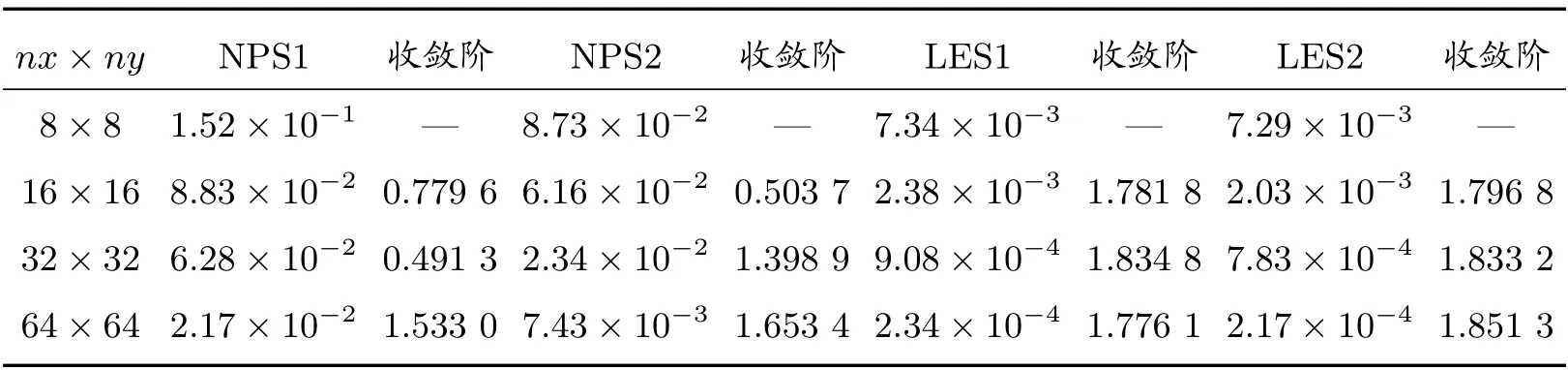
表6 算例2 在Shestakov 网格上的L2 误差及收敛阶

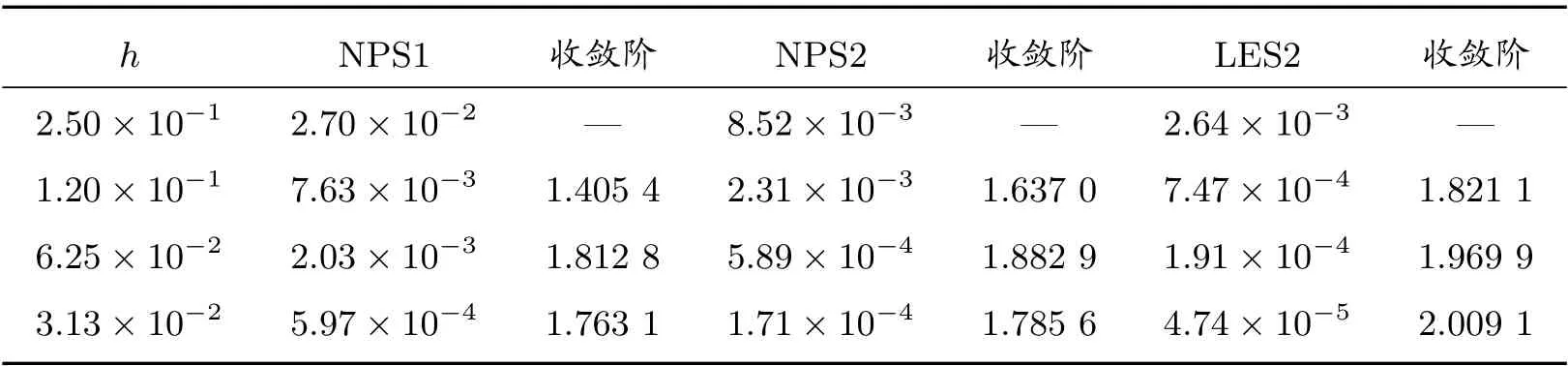
表7 算例2 在锐角三角形网格上的L2 误差及收敛阶

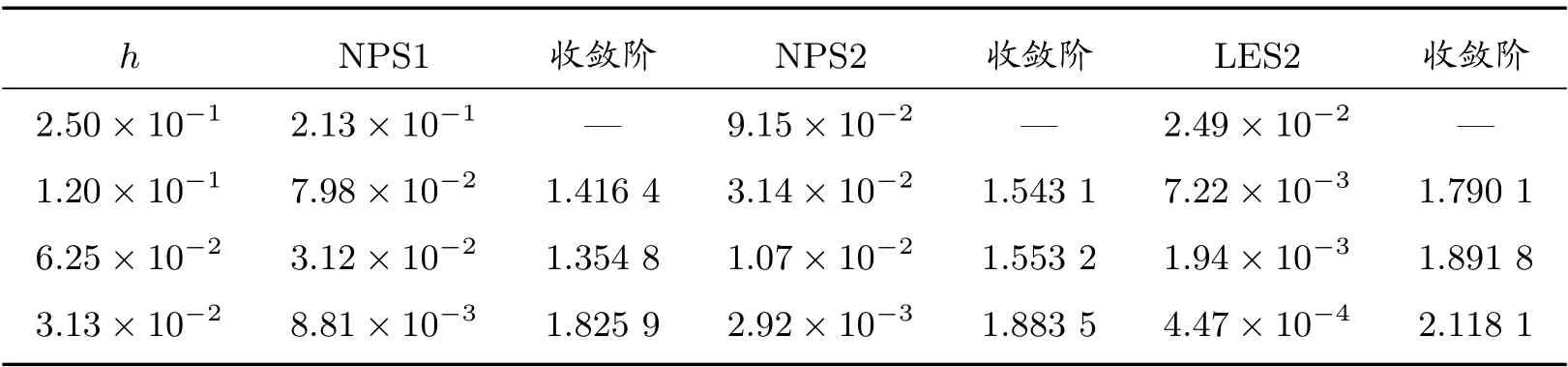
表8 算例2 在多边形网格上的L2 误差及收敛阶

算例3(扩散系数是间断常数) 在单位正方形区域[0,1]×[0,1]上，考虑具有如下间断扩散系数

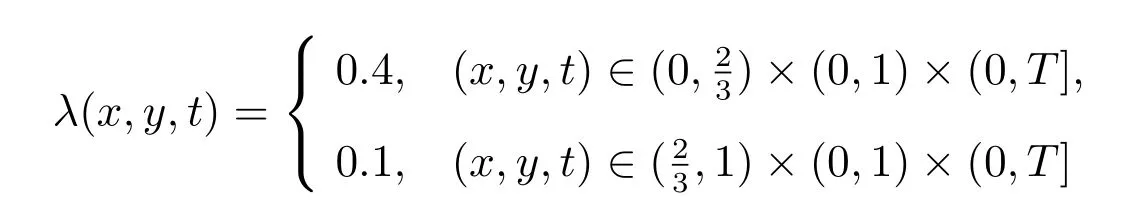
的情形，其精确解为

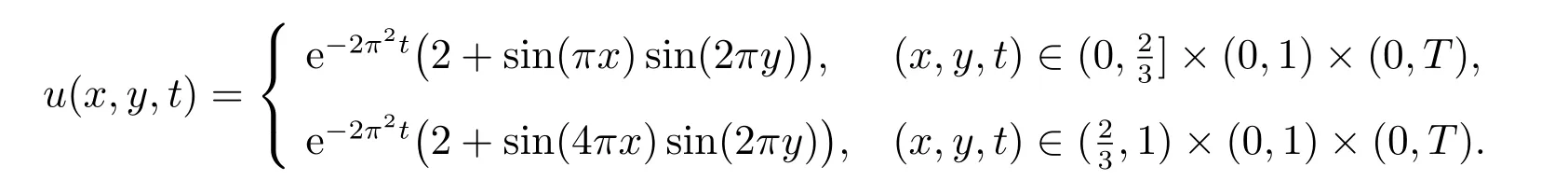
通过精确解可得出初始值、边界值以及源项。

对于此间断扩散系数的情形，表9 和表10 分别列出的在T= 0.1 时刻四种算法在随机四边形网格和Shestakov 网格上的计算结果表明，LES1 算法和LES2 算法仍然达到了二阶收敛速度。表11 和表12 给出了在锐角三角形网格和多边形网格上的计算结果，时间步长Δt的选取同算例1，LES2 算法依然可以达到二阶收敛，计算精度和收敛阶都优于NPS1 和NPS2。

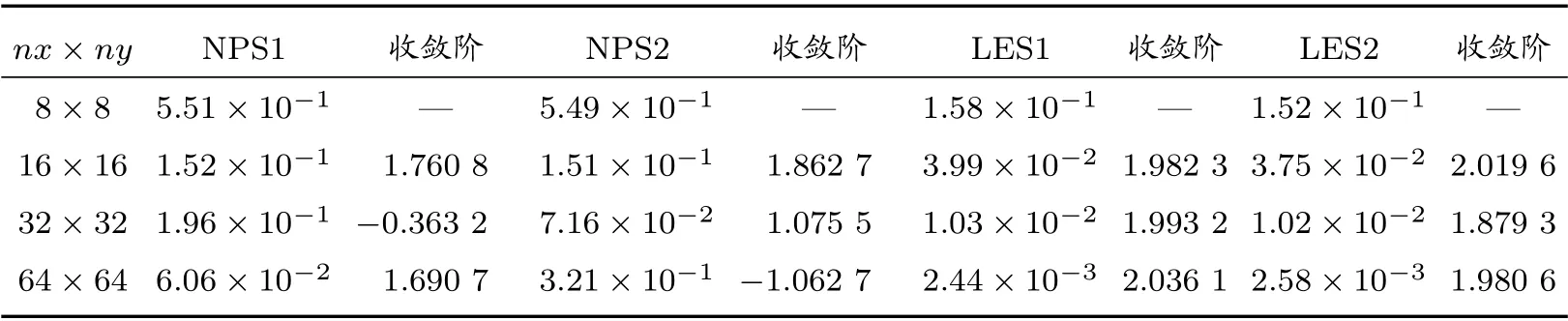
表9 算例3 在随机四边形网格上的L2 误差及收敛阶

表10 算例3 在Shestakov 网格上的L2 误差及收敛阶

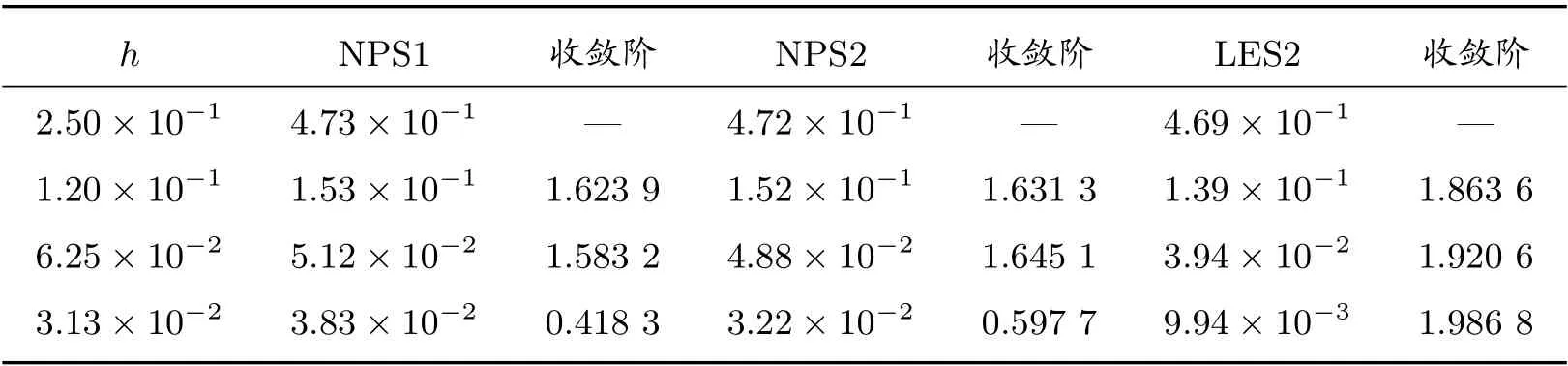
表11 算例3 在锐角三角形网格上的L2 误差及收敛阶

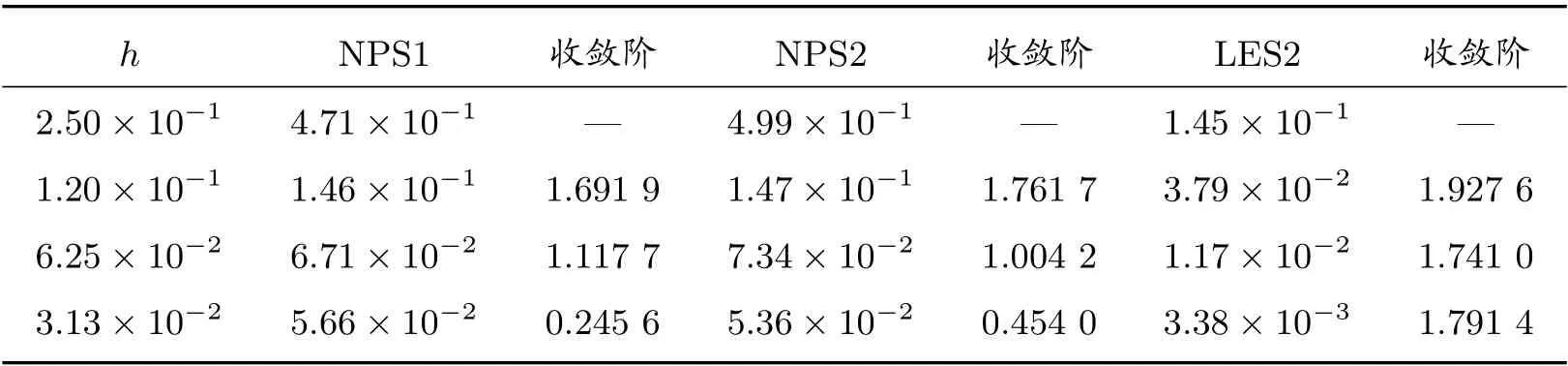
表12 算例3 在多边形网格上的L2 误差及收敛阶

算例4(对线性函数的测试) 在单位正方形区域[0,1]×[0,1]上，考虑如下非定常扩散方程

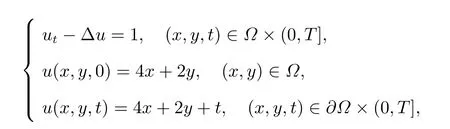
其精确解

u(x,y,t)=4x+2y+t.

由于LES1 和LES2 都是线性精确的，为此我们考虑解析解是关于自变量的线性函数，且扩散系数是常数的情形，理论上来说LES1 和LES2 的计算结果应该只出现舍入误差。表13 和表14 分别列出了在T= 0.1 时刻四种算法在随机四边形网格和Shestakov 网格上的计算结果，LES1 算法和LES2 算法得到了基本正确的计算结果。同样，表15 和表16 给出了在锐角三角形网格和多边形网格上的计算结果，LES2 算法也明显优于NPS1 和NPS2。

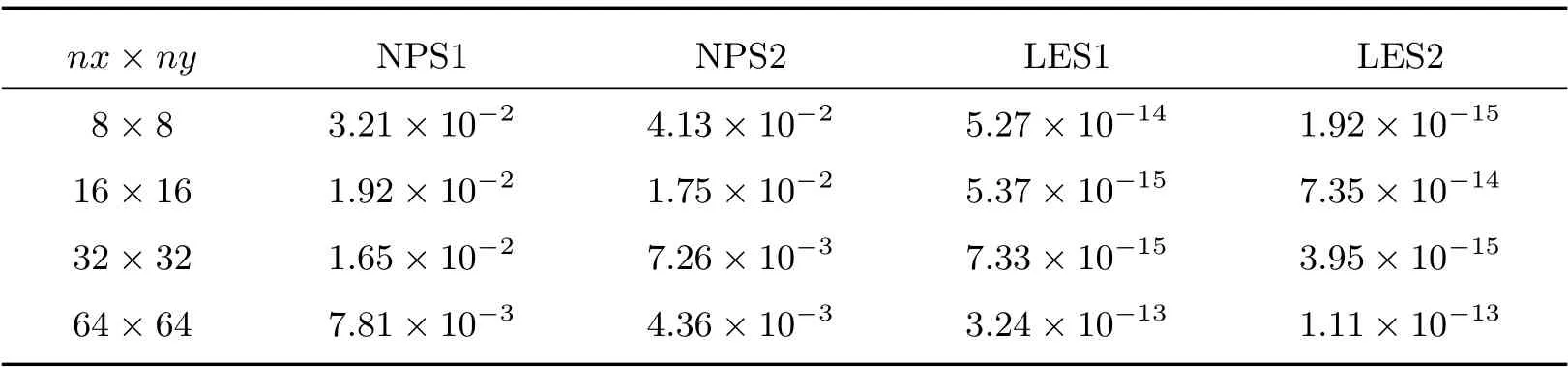
表13 算例4 在随机四边形网格上的L2 误差

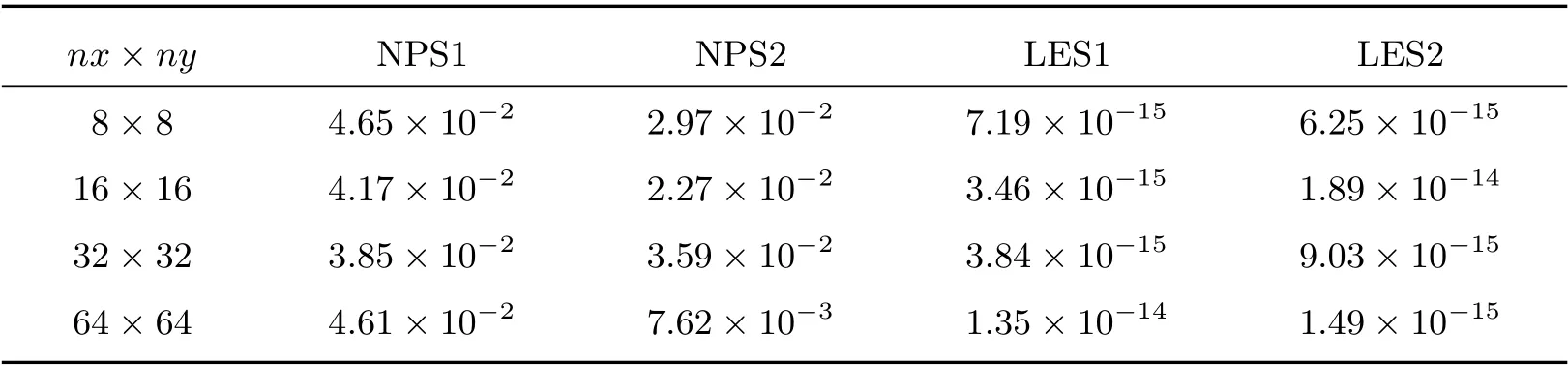
表14 算例4 在Shestakov 网格上的L2 误差

表15 算例4 在锐角三角形网格上的L2 误差

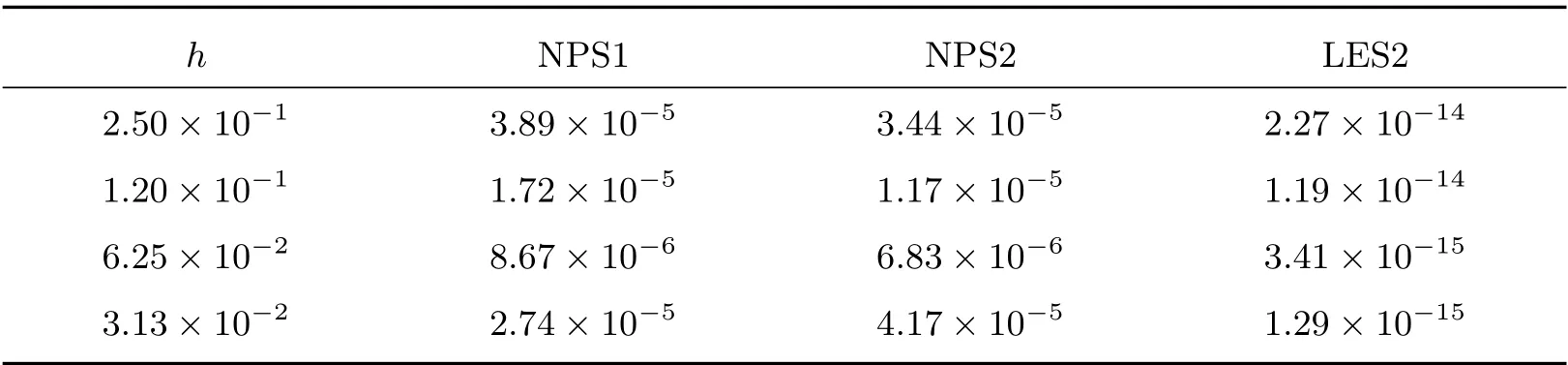
表16 算例4 在多边形网格上的L2 误差

算例5(非线性扩散方程) 在单位正方形区域[0,1]×[0,1]上，考虑如下非线性的非定常扩散方程

ut-∇·(λ(u)∇u)=f(x,y,t,u), (x,y,t)∈Ω×(0,T],

这里取λ(u)=+1，其精确解为

u(x,y,t)=et(2y3-3y2+3)(2x3-3x2+2).

初始条件、边界条件及源项由精确解的表达式相应确定。

对于非线性方程，方程组的系数矩阵及右端向量不但与网格形状有关，而且与解析解u有关，计算的过程中我们采用上一个时间步的数值解替代其中的解函数值。表17 和表18 分别列出了在T=0.1 时刻四种算法在随机四边形网格和Shestakov 网格上的计算结果，LES1 算法和LES2 算法均可达到二阶收敛速度。表19 和表20 给出了在锐角三角形网格和多边形网格上的计算结果，同样验证了LES2 算法的优越性。

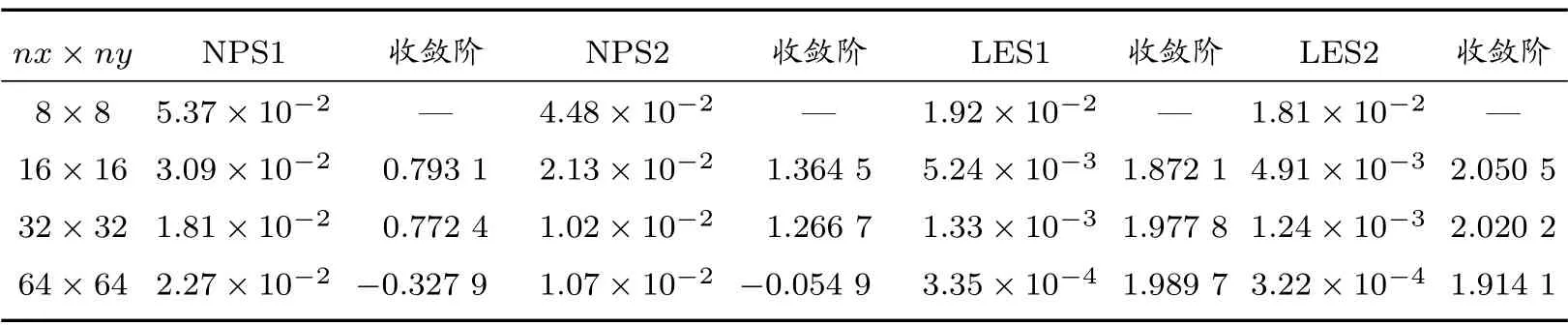
表17 算例5 在随机四边形网格上的L2 误差及收敛阶

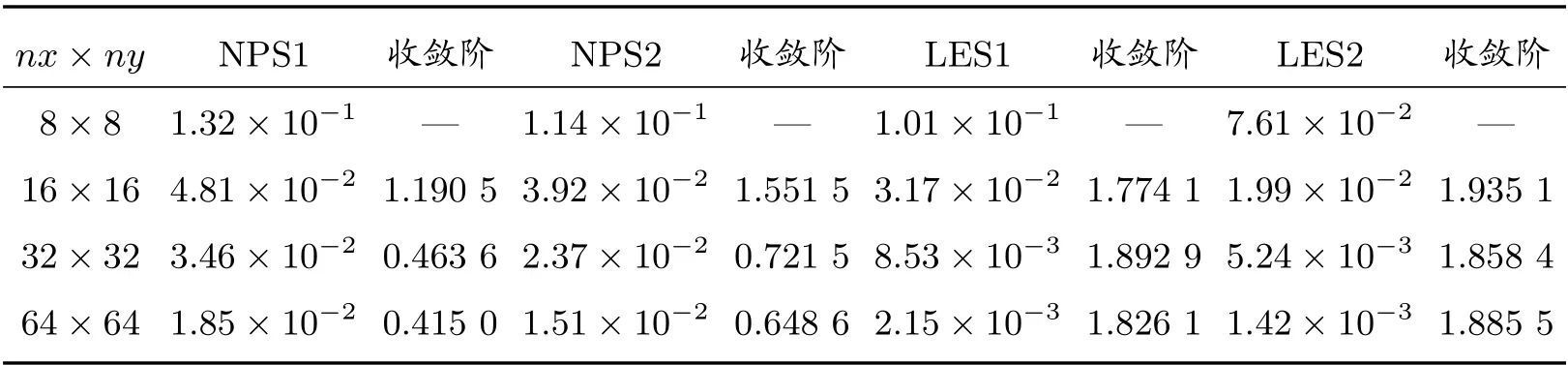
表18 算例5 在Shestakov 网格上的L2 误差及收敛阶

表19 算例5 在锐角三角形网格上的L2 误差及收敛阶

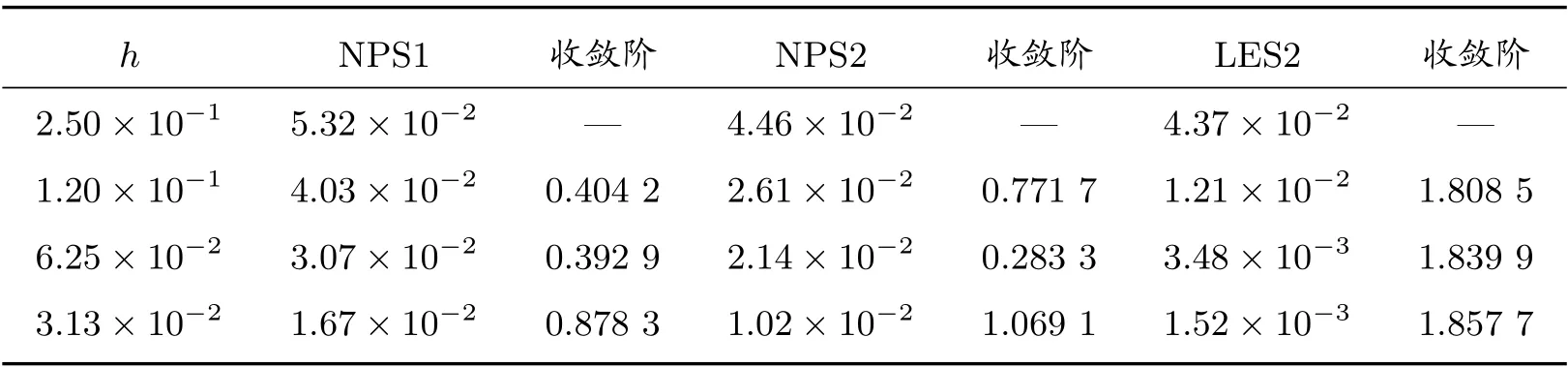
表20 算例5 在多边形网格上的L2 误差及收敛阶

3 结论

本文针对二维非定常扩散方程，提出了一种新的单元中心型有限体积格式，通过求解一个欠定方程组，确定网格节点的拟合系数。该方法不局限于四边形网格，理论上可以应用于任意多边形网格。针对具有连续和间断的乃至非线性扩散系数的非线性扩散方程，数值算例结果均表明，在随机四边形网格、扭曲的Shestakov 网格、锐角三角形网格和多边形网格上，新格式均可以保持L2误差的二阶收敛性。