具有分数阶形状记忆合金系统的时滞反馈控制与稳定性分析

王进斌, 马立峰

(1. 太原科技大学机械工程学院，太原 030024; 2. 太原科技大学应用科学学院，太原 030024)

0 引言

形状记忆合金(SMA)[1–5]是一类具有功能材料和智能材料特性的合金。基于其良好的记忆和力学性能，它已广泛应用到航天、电子、生物医学等领域中。目前，文献[6–7]研究了一类受负载和温度变化因素下SMA 振子在平衡点处的稳定性、分岔性质及混沌。2019 年，Yue 等[8]建立了SMA 薄板横向振动的非线性动力学模型如下

通过使用Galerkin 方法，方程(1)可转化成一类常微分方程的形式

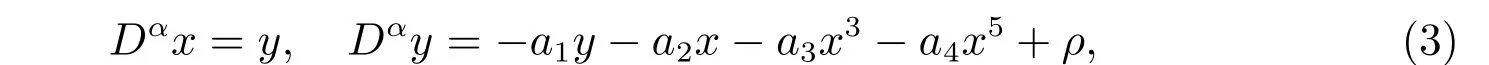
1 稳定性分析

令系统(3)的平衡点为E(x*,0)，容易发现x*满足

-a2x-a3x3-a4x5+ρ=0

系统(3)在E(x*,0)处的线性化特征方程为

其中b1=-a1,b2=-a2-3a3(x*)2-5a4(x*)4。

假设λ=reθi(r ＞0,θ=)，将其代入方程(4)，并分离实虚部得

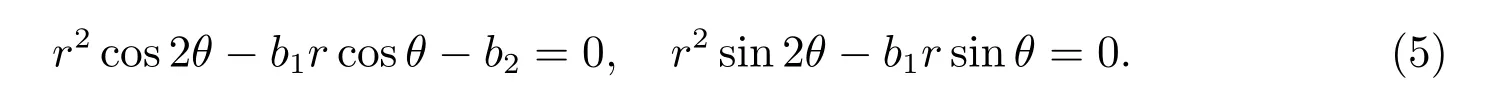
进一步计算得到

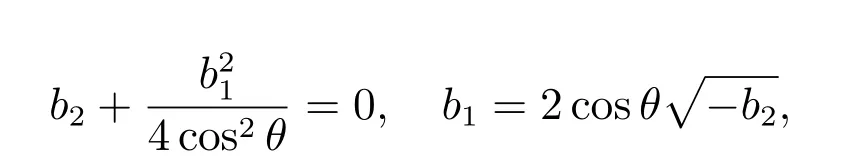
其中b2＜0。基于文献[14]和上述的分析，可得如下定理。

定理1对于系统(3)，如下结论成立：

“不会吧？据我所知，小区里所有的防盗门都是同一个品牌，这个品牌的防盗门在全国范围内有着较高的知名度，销路很不错，怎么会存在严重的质量问题呢？”

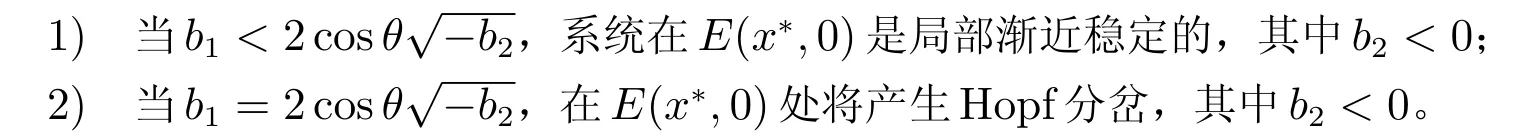
证明 令

为了进一步实现系统(3)的Hopf 分岔控制，这里使用如下形式的时滞反馈控制器

其中c1和c2是反馈参数。系统(3)可修改成

令X=x-x*,Y=y，控制系统(6)将变为

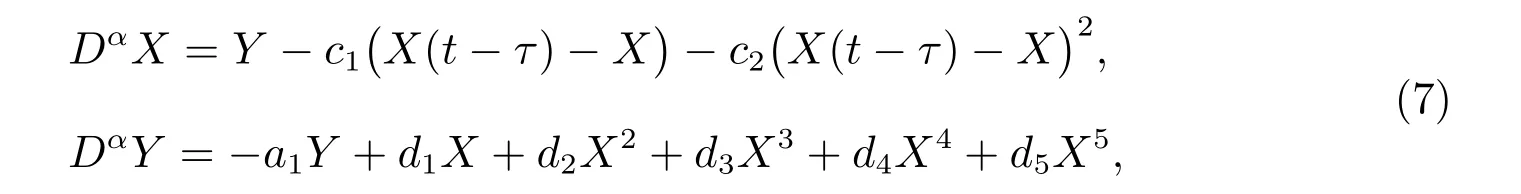
其中

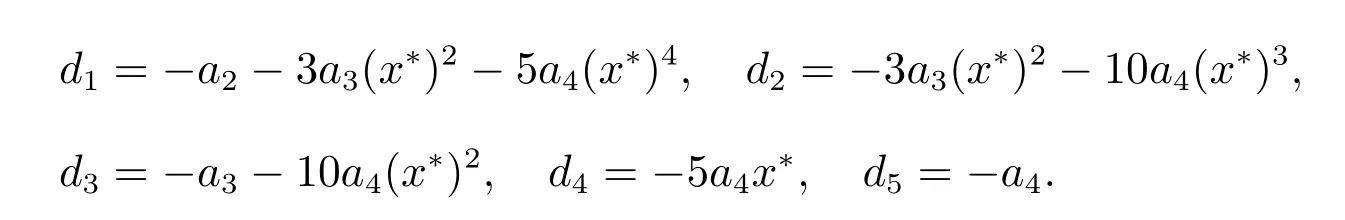
进一步，控制系统(6)对应其线性化特征方程为

其中

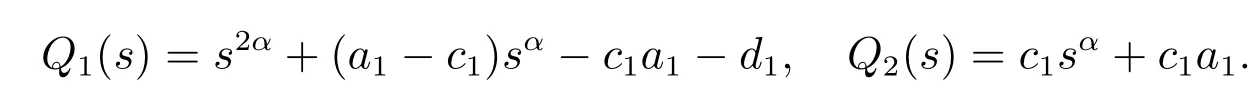
假设

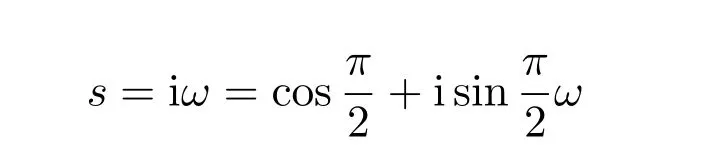
是方程(8)的根，进而计算得到

F(ω)=e1ω8α+e2ω7α+e3ω6α+···+e8ωα+e9=0,

其中

利用sin2ωτ+cos2ωτ=1，我们得到

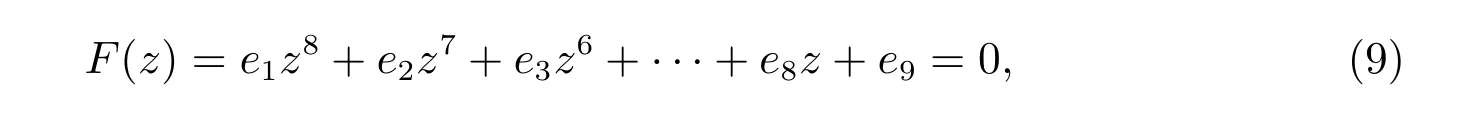
其中

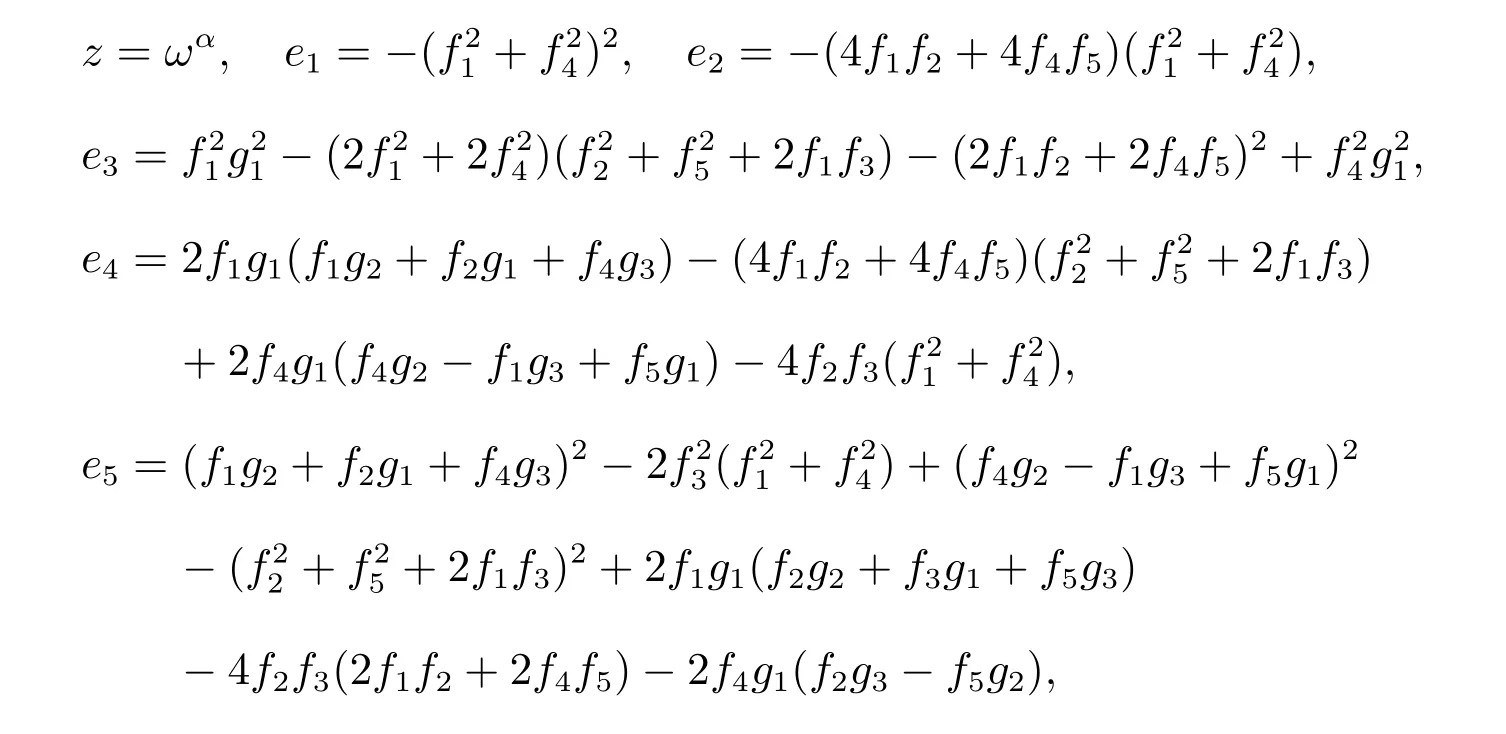
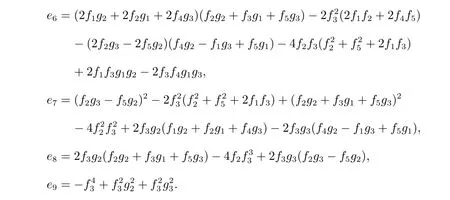
不失一般性，我们假设上述方程至少有一个正根

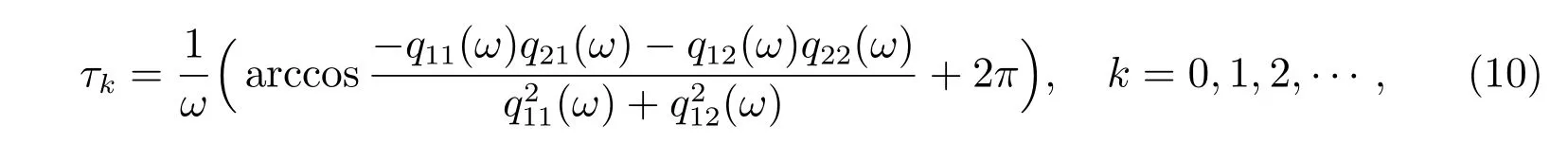
其中τ0=min{τk},k=0,1,2,···为分岔点。

对方程(8)两边关于τ求导，进行计算得到

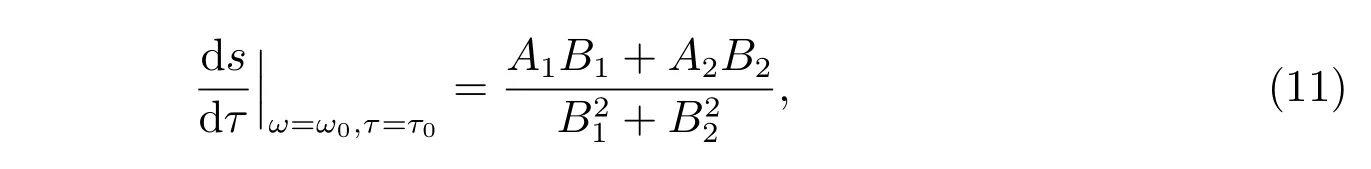
其中

进一步得到如下定理。

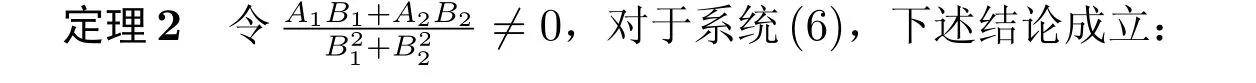
1) 当τ ∈(0,τ0)，平衡点E(x*,0)是局部渐近稳定的；

2) 当τ=τ0，在平衡点E(x*,0)将产生Hopf 分岔。

此外，利用Adams-Bashforth-Moulton 数值模拟方法，并选取参数a1= 0.1,a2=-0.1,a3=-2,a4=2,ρ=0.08,h=0.08。图1 的显示结果验证了定理2 的结论。

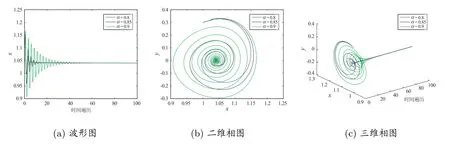
图1 系统(6)的波图和相图，分数阶α=0.8、0.85 及0.9, h=0.05, (x0,y0)=(1,0.3)和τ =0.2

2 结论

本文研究了一种分数阶SMA 振荡器，并给出了系统稳定性和Hopf 分岔存在的条件。文章得到的稳定性判据表明，分数阶对SMA 振子系统的稳定行为和分岔特性起着关键作用。此外，为了控制分数阶SMA 系统，我们设计了一个非线性延迟反馈

u(t)=-c1(x(t-τ)-x)-c2(x(t-τ)-x)2,

并得出时滞τ和分数阶α对控制系统动力学特性有重要影响。