H(curl)空间中椭圆最优控制问题的自适应有限元算法

贺之龙, 赵建平, 杨 欢, 李 兵, 席梦茹

(新疆大学数学与系统科学学院，乌鲁木齐 830017)

0 引言

本文主要讨论了基于Maxwell 方程组的磁测问题[1]

其中三维矢量场H、B和J分别表示磁场强度、磁感应强度和电流密度。考虑区域Ω ⊂R3为一个带有Lispschitz 边界Γ的有界区域，给出相应的渗透率μ与x和B无关的控制参数，磁导率ν为渗透率的倒数μ-1。根据高斯磁定律，存在磁向量y满足以下公式

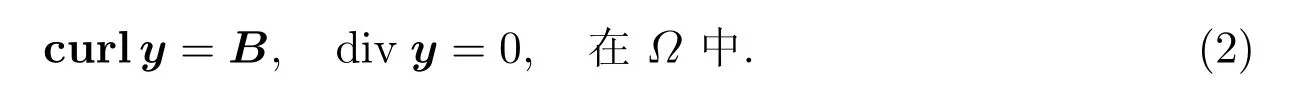
结合(1)式和(2)式，考虑一个完美的电边界条件，得到椭圆边值问题

这里n是Γ的外法向量。通常，我们认为控制域Ωc ⊂Ω是由Lipschitz 边界∂Ωc连接，考虑以下椭圆最优控制系统

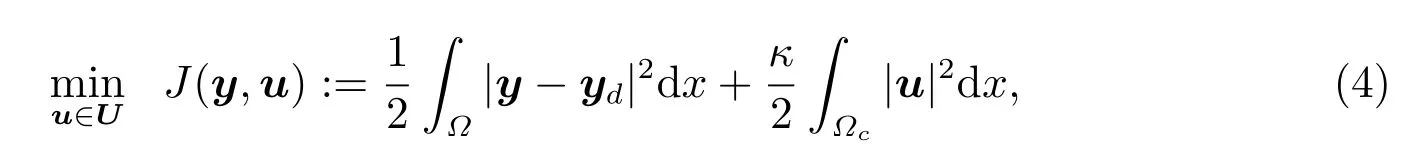
满足约束方程

其中κ ∈R+为控制参数，yd ∈L2(Ω)为y的期望值，χΩc为Ωc的特征函数，nc是Γc:=∂Ωc的外法向量。考虑到无散度对电流u的无散度约束，以及电荷守恒定律，根据(5)式中的容许空间的定义，由旋度算子的分布定义

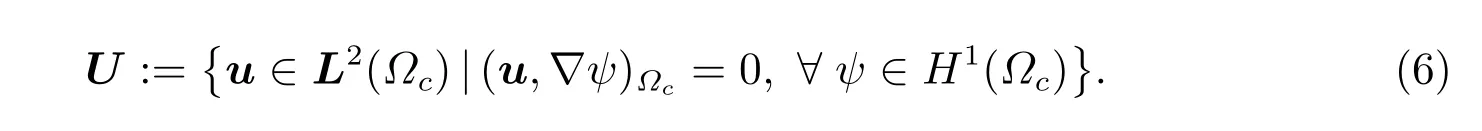
近年来，受偏微分方程(PDE)约束的最优控制问题已成为一个非常有趣的跨学科课题。它具有非常广泛的应用，涵盖物理、化学和其他领域，如储层管理、热现象和磁场等问题[2]。相对而言，自适应有限元求解Maxwell 方程组的理论比较成熟[3–6]，二阶线性椭圆问题的研究结果已经广为人知[7–10]。文献[11]的研究成果给出了Maxwell 最优控制问题在点态约束下的正则化结果，建立了一种最优控制算法估计了H(curl)范数离散化误差，并进行了数值验证，自适应有限元理论也通过自适应边界元推广到Maxwell 方程组中[5,8,12–13]。

基于自适应有限元方法(AFEM)的特点，可以提高电磁场计算效率及求解精度。本文用AFEM 求解H(curl)空间中的椭圆最优控制问题，研究相应的收敛性分析。很多学者分析了H1椭圆方程和Maxwell 方程自适应有限元数值解的收敛性，也有文献中对H(curl)空间中变系数椭圆问题、常系数正弦时变Maxwell 方程收敛性做了详细的证明[13–14]。除此之外，文献[15–16]也采用自适应边界元方法求解静磁场最优控制问题和变系数正弦时变Maxwell 模型(1)，并分析其收敛性。

为了求解偏微分方程，学者们提出了多种有效的方法，其中AFEM 是最常用的方法。对于给定的区域，AFEM 使用后验误差估计子来引导网格细化，从而确保特定区域解更难估计的节点密度更高。AFEM 是一种可以自动调整网格算法以改进求解过程的数值方法，采用AFEM，只需确定初始网格和可接受的误差范围，计算机即可生成满足要求的网格，大大提高了分析效率和结果的可靠性。AFEM 涉及以下循环

求解方程→误差估计→更新求解,

其中误差估计模块可以评估有限元的精度。将新网格与旧网格紧密相连，从而将旧网格划分后的误差分布信息有效地反馈给重新划分的网格，使自适应网格能够快速迭代。如文献[17]，针对P-Laplace 问题，利用AFEM 进行先验误差和后验误差分析，证明了该方法误差的衰减速率，特别是对于线性椭圆和抛物型问题[18–22]。此外，关于椭圆最优控制问题也有很多有限元分析[23–26]。

求解Maxwell 方程组的方法有很多，如间断Galerkin 有限元法[27]、人工边界条件的吸收法[28]和谱方法[29]。本文将AFEM 应用于求解H(curl)空间中的椭圆最优控制问题，并对其收敛性进行了研究。

文章内容概述如下：在第1 节中，我们定义了空间并推导混合变分形式，将最优控制问题转化为偏微分方程组，给出了偏微分方程解的存在唯一性；在第2 节中，我们提出了自适应有限元方法并进行误差分析；在第3 节中，两个数值算例验证了我们可以得到最优解，证实了算法的可行性；最后一节给出本文的总结。

1 预备知识

1.1 空间及其性质

本文考虑的函数和向量都是实值的，下面定义了一些空间。在后面的分析中，我们的主要工作是基于以下函数空间

其中Ω和Ωc是三维欧氏空间R3中的Lipschitz 边界多面体区域，n和nc分别是∂Ω和∂Ωc单位外法向量。

此外，为了便于以后的分析，给出了Helmholtz 分解、一些重要的不等式和infsup 条件。Helmholtz 分解是指任何具有足够平滑度且快速衰减的高维向量场可以分解为两个不同的向量场的和。根据文献[30]第3 节，文献[31]第3.7 节以及文献[32]的引理4.3，可知L2(Ω)d存在多种Helmholtz 分解形式。

根据需要，本文主要讨论了以下Helmholtz 分解形式[1]

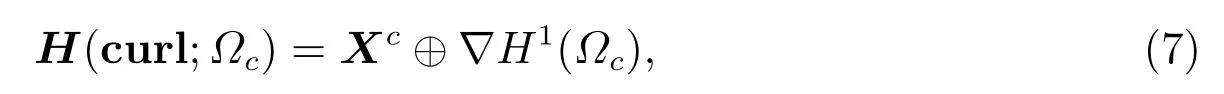
这里Xc ⊂H(curl;Ωc)定义为

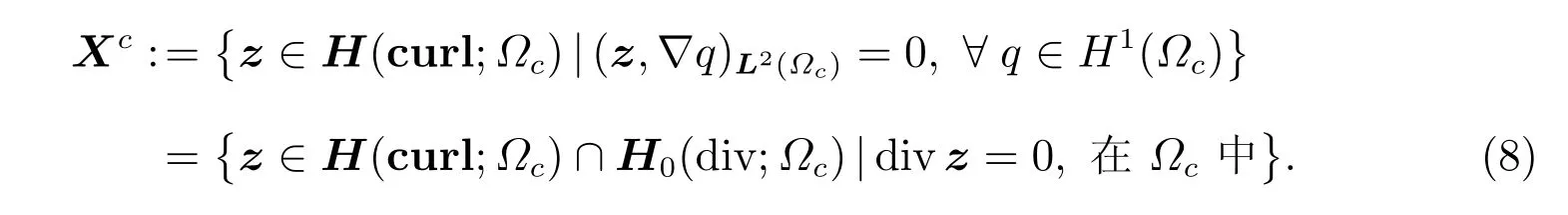
Poincar´e 型不等式[1,33–34]如下所示

inf-sup 条件如下所示

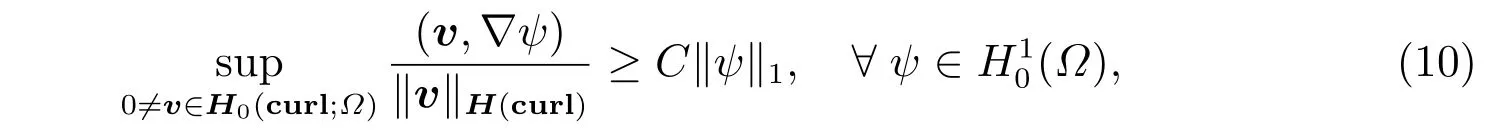
这里C仅依赖于Ω和X如下定义

X:={z ∈H0(curl;Ω)|(z,∇q)=0,∀q ∈H10(Ω)}.

1.2 最优系统

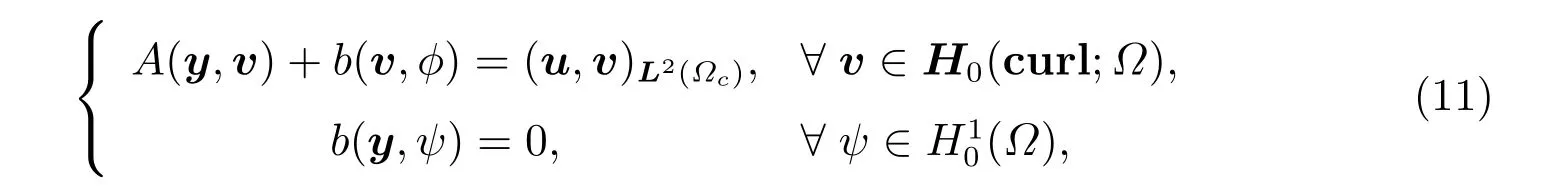
考虑状态约束的混合变分形式(5)，寻找满足以下条件的y ∈H0(curl;Ω),φ ∈H10(Ω)，有这里φ表示拉格朗日乘子，v和ψ为试探函数，其中双线性函数A(·,·) :H0(curl)×H0(curl)→R 和b:H0(curl)×H0→R 的定义如下

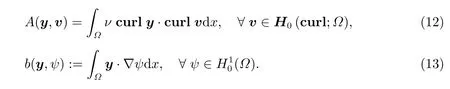
我们注意到A(·,·)是对称的，由于H0(curl;Ω)是Hilbert 空间，双线性形式A(·,·)满足连续性和强制性。因此混合变分形式(12)和(13)式具有线性鞍点构造。为了建立Gˆateaux 导数，我们引入一个向量函数

F(s)=νs.

利用此函数，双线性函数A(·,·)可表示为

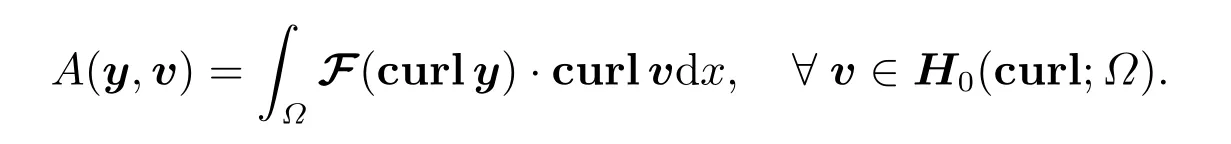
接下来引入Jacobi 矩阵函数

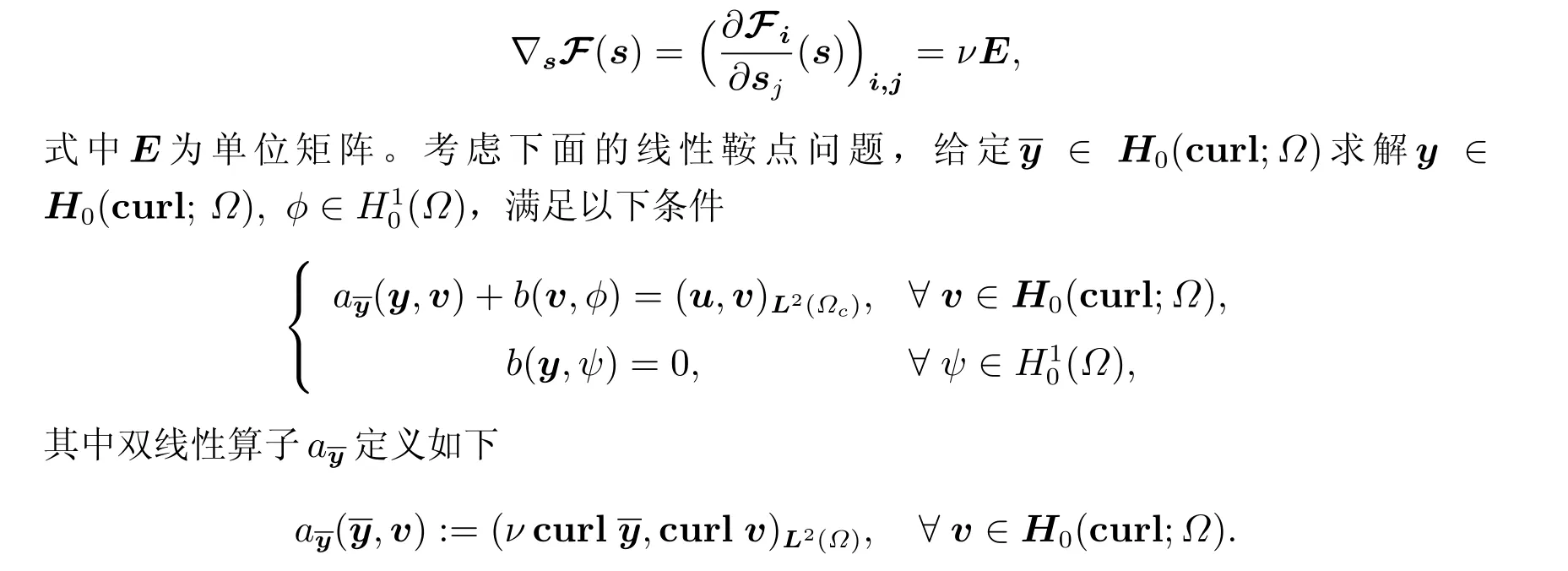
接下来，我们将控制变量到状态变量的映射算子G表示为

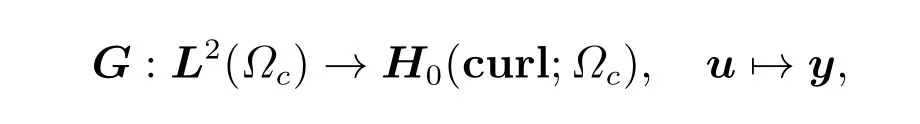
对于每一个u ∈L2(Ωc)，问题(11)存在唯一解y。然后，考虑L2(Ω)范围内的G，将映射算子表示为

S:L2(Ωc)→L2(Ω),S=IG,

这里I:H0(curl;Ωc)2(Ω)。

建立了Gˆateaux 导数之后，设u是(4)式的最优控制，其中相关状态y=G(u)，则目标函数f:L2(Ωc)→R 如下所示

其中S′()q=y由下面方程的唯一解给出

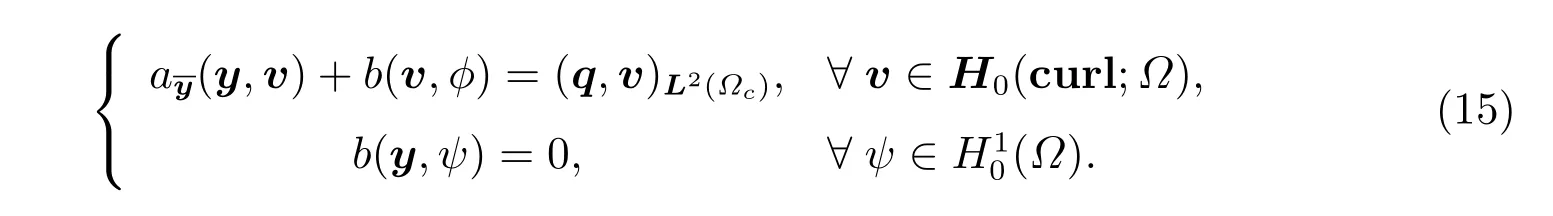
我们现在引入由以下线性鞍点问题定义与(4)式相关的伴随方程

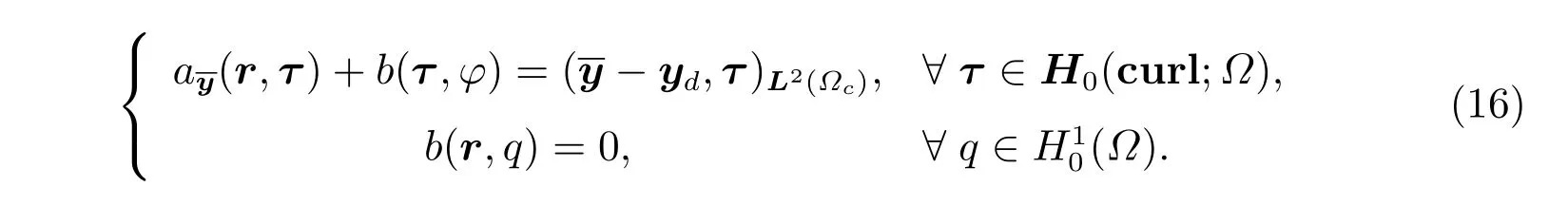
下一步，让τ=S′()q=y代入(16)式，v=r代入(15)式，结合(14)式，然后考虑b(y,ψ)=b(r,q)=0，我们得到

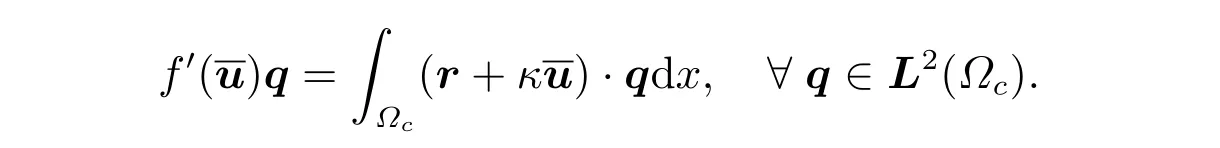
接下来，我们主要讨论系统(4)的最优控制问题。由于最优性条件是优化问题的局部或全局最优解必须满足的条件，我们首先考虑系统(4)的最优性条件，结合前一节的准备工作，证明存在唯一解，并可以用以下充分最优条件来描述

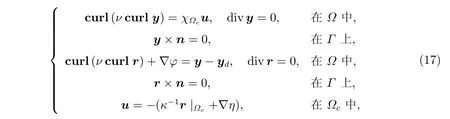
其中r ∈H0(curl)是伴随状态，φ ∈H10是对应于r的Lagrange 乘子，η ∈H1(Ωc)为u的Lagrange 乘子。

根据变分原理，我们将(17)式写为变分形式，控制u*∈U，伴随状态r*∈H0(curl;Ω)和对应的Lagrange 乘子φ*∈(Ω)，状态y*∈H0(curl;Ω)和对应的Lagrange 乘子φ*∈(Ω)，则一阶最优性条件由以下方程组成

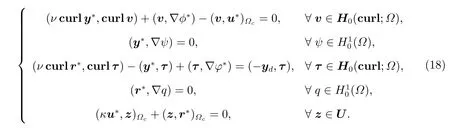
根据(6)式可将η消除。

如果将变分形式(18)直接用有限元进行离散化，在有限元空间中仍然存在无散度的条件，这增加了离散理论分析的难度。因此，我们将给出变分问题解空间的性质，目的是体现离散空间的无散度条件。

假设1[1]设区域D是一个Lipschitz 多面体区域，满足⊂D ⊂Ω和

假设的合理性参见文献[1]中注4.2。

引理1[1]若假设1 是正确的，则(18)式每个最优控制都存在较高的正则性

如果Ωc是C2,1类，则∈H2(Ωc)，其中指数σc和详细证明见文献[1]中定理4.3。

2 有限元离散和误差分析

由于解空间是一个无限维空间，(18)式除了在极少数的特殊情况下，通常很难得到问题的精确解，所以有必要采用有限元离散方法近似求解。变分将无穷维空间中的问题(18)转化为有限维空间中，有限维度空间也被称为有限元空间。

我们介绍自适应有限元离散方法求(4)式和(18)式的解。设T是形状规则的正则三角剖分，是一个封闭的四面体集合，分割后的不相交元素记为T，满足，任意元素T是准正则的。如果T和T′都属于T，则最多只能有一个公共曲面。我们选择局部网格大小hT:=，于是，限制在控制域上的Ωc和T引发一个上的形状规则的三角剖分子集T c。然后，将有限元空间VT定义如下

VT={v ∈H0(curl;Ω)|vT=v|T ∈(Pi(T))3,∀T ∈T,i=1,2,3},

其中Pl(T)表示在T上定义的一组多项式，次数不大于l，l是一个给定的正数且l ≥1。

记V cT:=VT|Ωc和H1(Ωc)相容的分段有限元空间为，则离散控制区域变成如下形式

记录区域离散后的节点集，Hτ(curl)和分别记为{xi},i= 1,2,···,N和{xk},k= 1,2,···,M。然后，我们选择节点型基函数，建立有限元空间，Hτ(curl)基函数由Bτ(curl) :={αi(x) :i= 1,2,···,N}表示，基函数由Bτ(L2):={βk(x) :k=1,2,···,M}表示。由

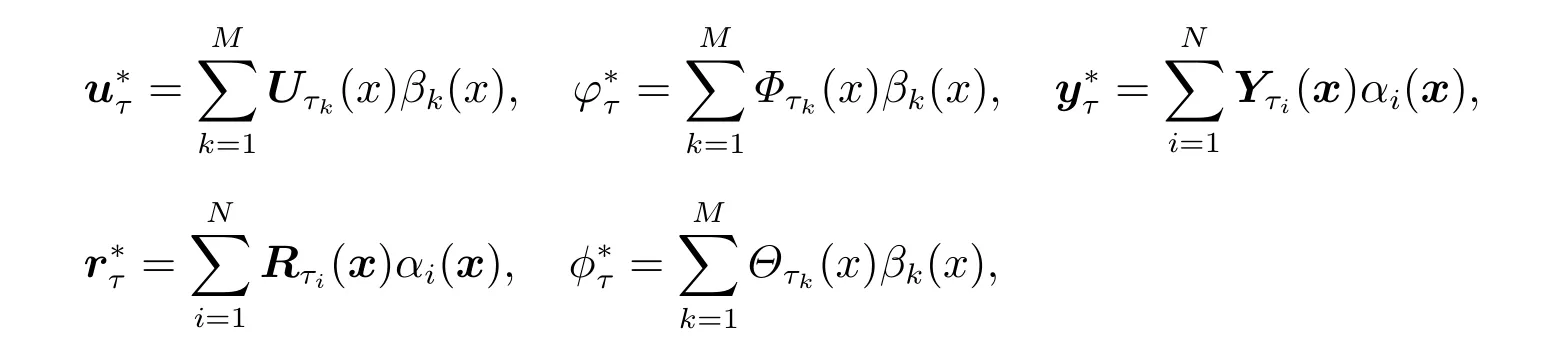
将(19)式写成如下等价矩阵形式

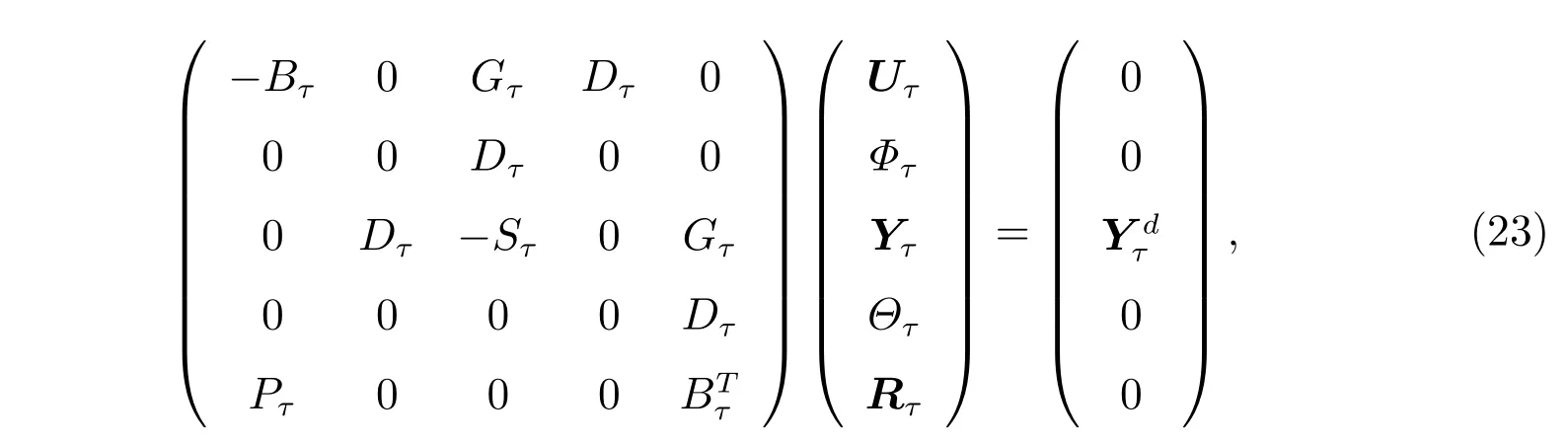
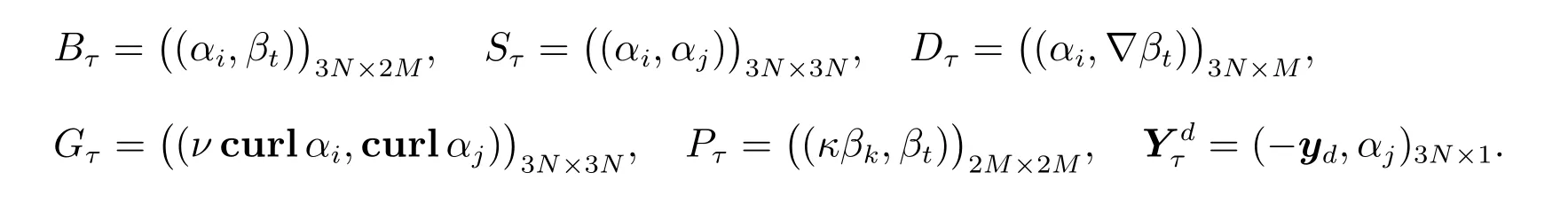
其中我们的数值模拟是根据有限元方程组(23)给出的，结合基函数给出矩阵形式，矩阵中的元素定义如下

由(22)式和所采用的基函数，可得(23)式为如下形式

在离散的情况下，(9)式和(10)式变成如下形式

其中C仅依赖于Ω和T，以及

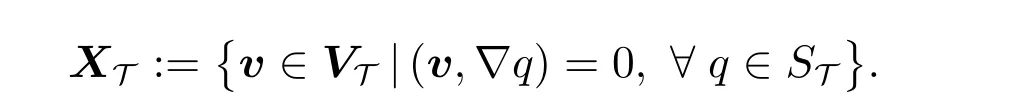
考虑Galerkin 正交性，我们将(22)式写成以下辅助鞍点系统

不等式(9)和inf-sup 条件(10)保证了问题(27)解的唯一性。

2.1 误差分析及其可靠性

下面讨论离散问题(22)的误差估计，并以相对于控制状态和伴随状态的误差来表明其可靠性。我们引入如下的符号和定义。

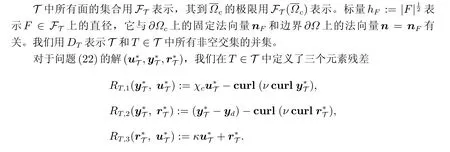
接下来，对每个M ∈T，我们引进误差估计子

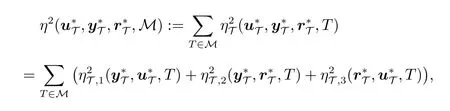
其中

成立。

证明 通过Helmholtz 分解H0(curl;Ω)=X ⊕∇(Ω)，得到

对任意的r ∈(Ω)，(w,∇r)=0，取v=w在第一个方程(27)中得到

其中用到分解w=∇φ+z,z ∈H1(Ω)∩H0(curl;Ω),ψ ∈Ω)。用算子ΠT表示z离散算子，用方程组(22)的第一个方程以及=0，我们推导出

类似地，T ∈T c,= 0 上，用(20)式和方程组(22)第一个方程vT=∇IT ψ，以及∇·在每个元素上为0，我们得到

然后，得到

利用‖w‖H(curl)和‖∇×w‖0之间的范数等价以及∇×w=∇×(y()-)，从(20)式中得到

另一方面，在(22)式第二个方程中得q=r,qT=IT r以及

于是，在(29)式中得到

证明 证明和引理1 类似，给出Helmholtz 分解和正则分解

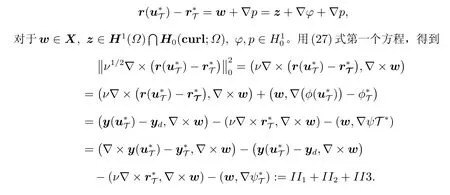
然后，通过Cauchy-Schwarz 不等式结合上述两个不等式，我们得到

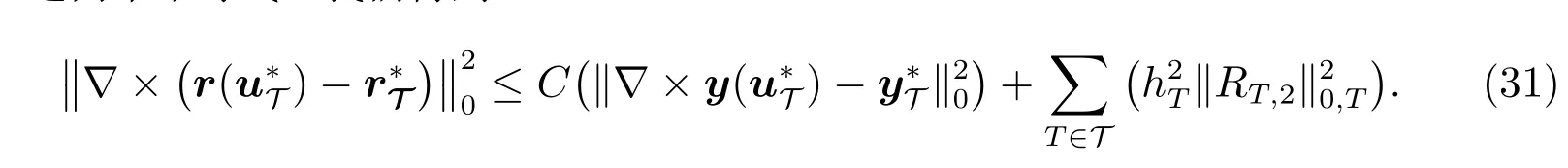
此外，我们可以用q=p,qT=IT p推出

由(31)式、(32)式以及估计(28)可以证明。

现在，我们确定误差估计子η的可靠性。

定理1设(u*,y*,r*)以及(,,)分别是(18)式和(22)式的解，则有

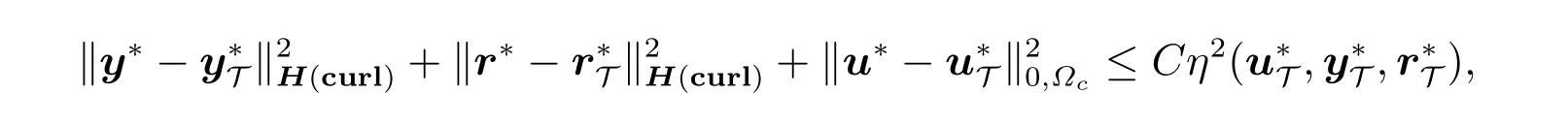
其中C由ν、κ和T决定。

证明 我们首先估计u*-u，从(8)式中得到，存在η*∈H1(Ωc)以及∈，于是

(18)式的第一个和第三个方程减去(27)式第一个和第三个方程，可以得到对任意的v ∈X，有

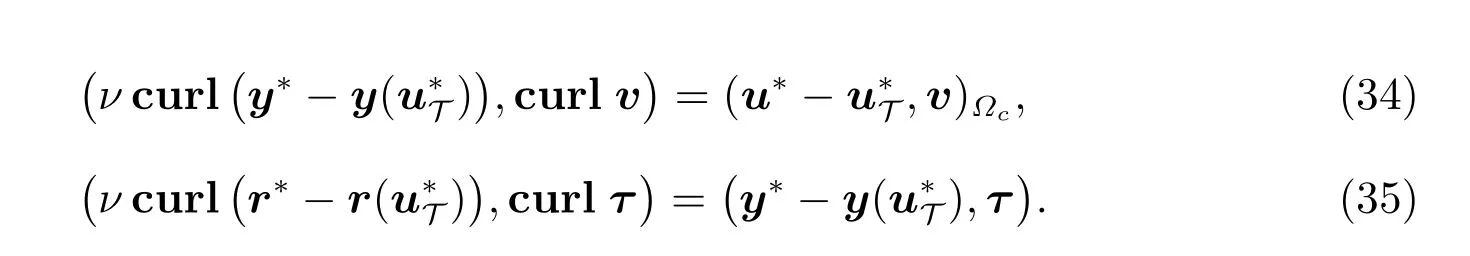
令(34)式中v=r*-r()，(35)式中τ=y*-y()，我们得到

根据U和UT的定义，(6)式、(21)式和Scott-Zhang 插值I:H1(Ωc)→[35]，可以得到

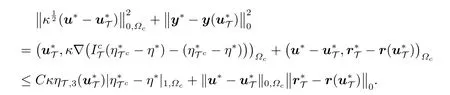
通过(30)式和(33)式，有

考虑到Young 不等式

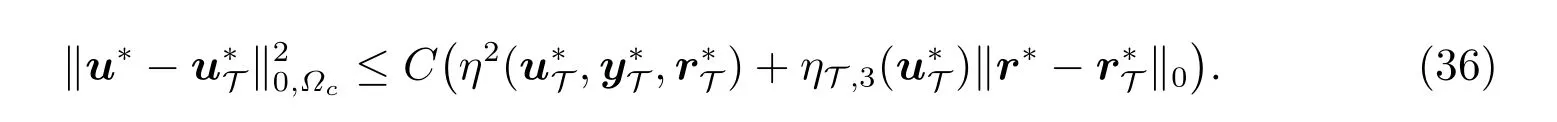
然后，在(34)式中令v=y*-y(u)，考虑到y*-y()∈X，再根据(9)式，可以得到

在(35)式中，令τ=r*-r()∈X，通过(9)式和(37)式推导出

通过(30)式和(36)式，考虑Young 不等式，得出

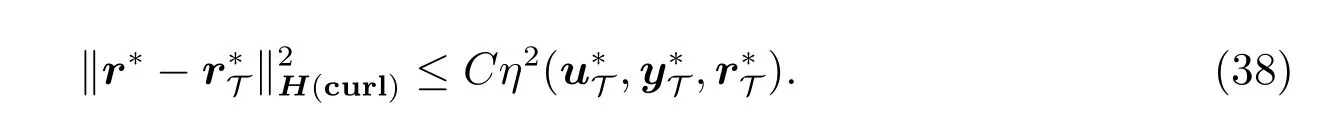
从(36)式和(38)式中，可以得出

在假设1 中，使用(37)式、(39)式和(28)式，我们得到

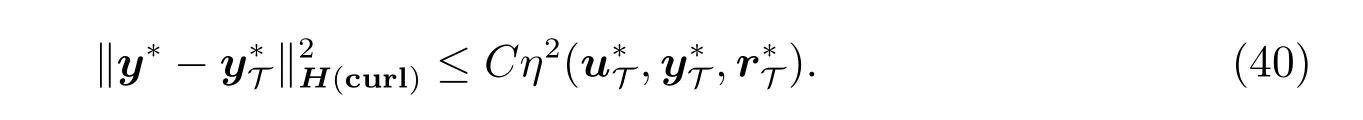
很明显，期望估计来自式(38)至式(40)。在特殊情况下，当我们采用一致加密时，误差阶是。

2.2 自适应算法

想要解决问题(4)和(11)，我们在问题(27)的基础上引入了有限元算法的后验误差估计。下面的分析需要更多的定义和符号。令T 为所有可能的由规则形状的初始网格连续剖分得到的一致三角形的集合[7,36]。对所有T,T′∈T，当T由T经有限二分得到T′时，我们称T′为T的细化。此外，对于每个三角形序列{T} ⊂T，Tk+1是Tk的细化，我们定义

算法1耦合算法

令k:=0，给定初始值uk

3. 网格细化，细化网格T ∈Mk通过二分法得到Tk+1；

4. 令k:=k+1，回到第1 步。

算法2解耦算法

令k:=0

3. 网格细化，更新网格T ∈Mk通过二分法得到Tk+1；

4. 令k:=k+1，回到第1 步。

此外，算法1 可以生成一系列线性元素空间Sk和Lagrange 乘子，和都等于零。在实际应用中，通常需要Mk包含误差指数最大的元素以提高计算效率，即

2.3 收敛性分析

给出近似解序列和一些极限离散空间是收敛分析的基础，由此我们定义极限空间[15]

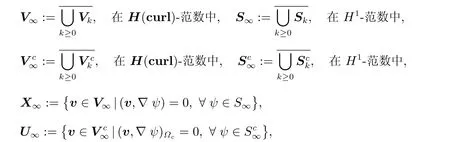
这里{Vk}和{Sk}都是由算法1 生成的，它们和离散空间有相同的性质。实际上，很容易从V∞和S∞的定义中看出

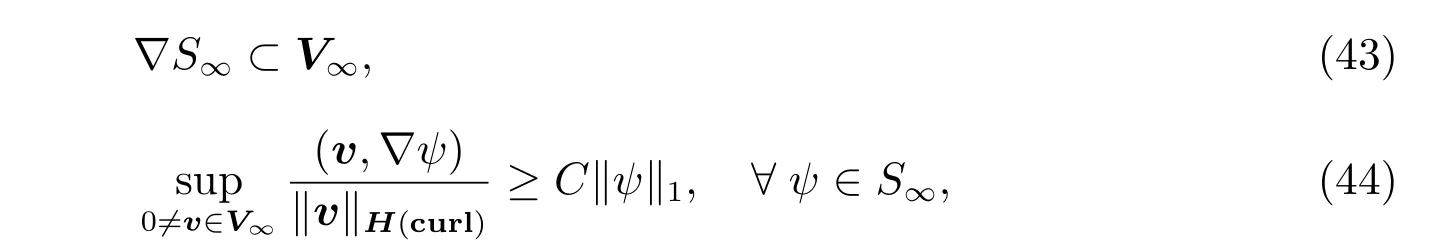
常数C只依赖于Ω。此外，当的闭子空间为∇时，其分解为

最后，我们记X0X1···X∞X。在X∞上有下列重要的结果对应(25)式。

引理4[15]对于任意的v ∈X∞，存在一系列{wk},wk ∈Xk，因此

wk →v,H0(curl;Ω),

常数C依赖于T0的形状正则性，因此‖v‖0≤C‖∇×‖0。

证明 我们可以把上面公式的等价形式写成

我们将分成两部分来证明收敛性。

第一部分：引入离散辅助问题

不难看出这个问题是混合公式(46)的有限元近似，所以根据Babuska-Brezzi 理论=0，得到

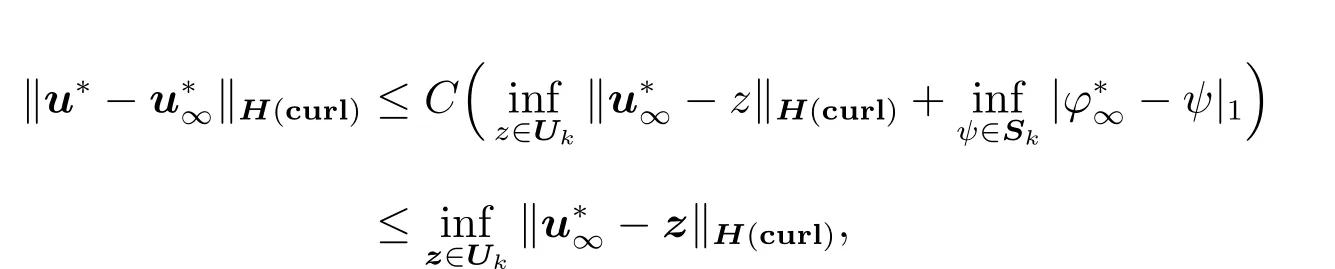
并通过减去(18)式来估计稳定性，得到

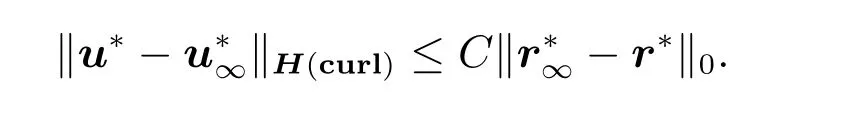
第二部分：对于问题(18)，我们只需要证明第一个等式。从(18)式中得到φ*=φ*===0，对于任意的v ∈H0(curl;Ω)，有

为了简化证明，我们需要对模型中的检测函数代入具体值，可得

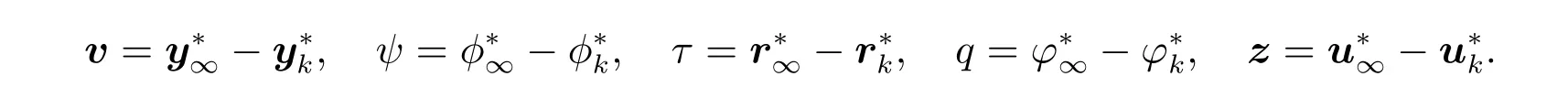
另外，设ν=κ= 1，在(27)式中将第一个公式和第二个公式相加，将第三个公式和第四个公式相加，可以写成

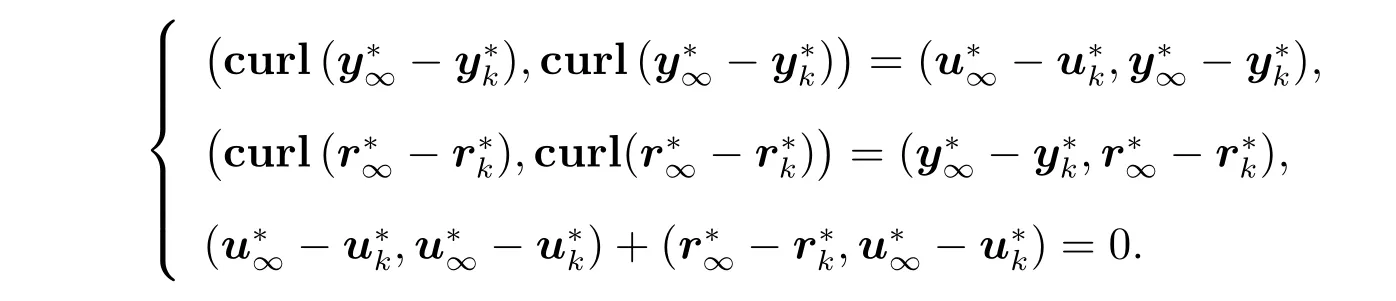
把上面方程中的三个方程结合

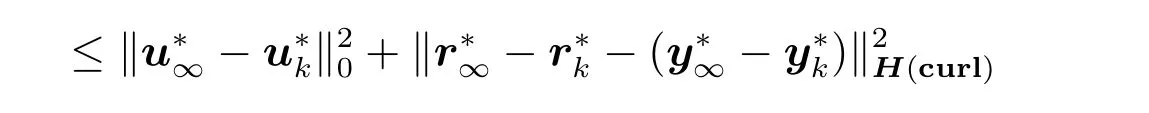
≤chp+1,c ＞0,k →∞,h →0.

由以上两部分，我们可以得出算法1 的主要收敛结果。

3 数值模拟

本文通过两个数值算例说明有限元法在旋度空间处理椭圆最优控制问题的合理性，利用迭代法来求解这个问题，主要是验证误差和收敛阶。

在本文描述的模型中取

Ω=(0,1)×(0,1),

yd=(cos(πy)sin(πx)+4π4cos(πy)sin(πx),

-cos(πx)sin(πy)-4π4cos(πx)sin(πy)),

模型的精确解如下

y=(cos(πy)sin(πx),-cos(πx)sin(πy)),

u=(2π2cos(πy)sin(πx),-2π2cos(πx)sin(πy)),

r=(-2π2cos(πy)sin(πx),2π2cos(πx)sin(πy)).

例1 解耦自适应有限元算法

对给定区域进行三角剖分、选取节点、求基函数，通过解耦算法，得到结果如表1 至表3 以及图1 所示。解耦的自适应有限元算法在下图表中简称为解耦算法，其中h为网格参数，n为网格划分次数。

表1 解耦算法中u*的相对误差及误差阶数

表2 解耦算法中y*的相对误差及误差阶数

表3 解耦算法中r*的相对误差及误差阶数

为了快速验证该方法的有效性，本文选取了二维问题进行求解。从图中的数值结果可以看出u*、y*和r*的误差阶数为2。随着h的减小，有限元解近似于精确解，与本方法的理论阶数一致。

例2 耦合的自适应有限元算法

我们用耦合算法对上述例子的误差进行了验证，结果如表4 至表6 以及图2 所示。耦合的自适应有限元算法在下图表中记为耦合算法。

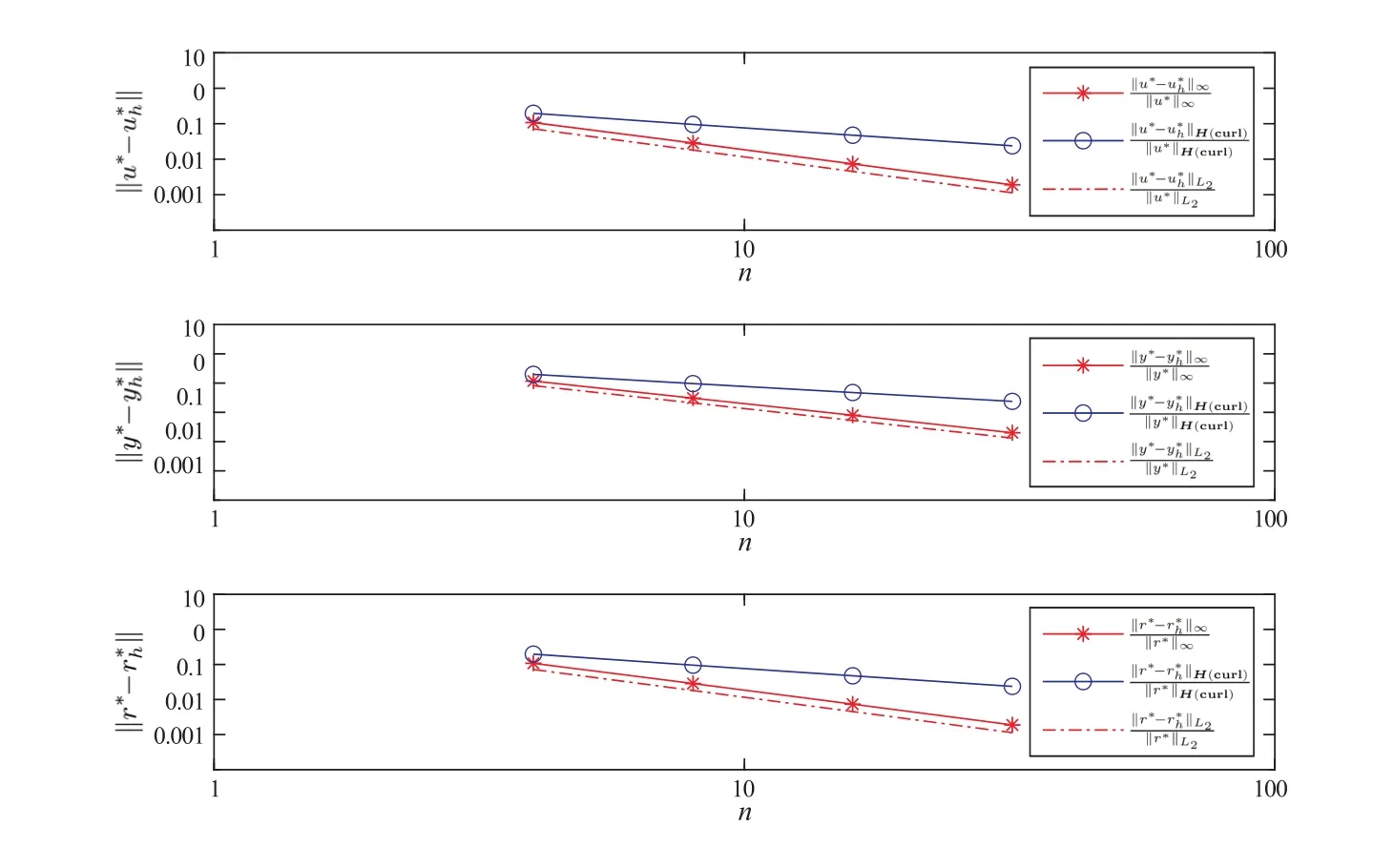
图2 耦合算法中u*、y*和r*的相对误差，其中n=

表4 耦合算法中u*的误差及误差阶数

表6 耦合算法中r*的误差及误差阶数

表5 耦合算法中y*的误差及误差阶数

数值结果表明，耦合算法的误差u*、y*和r*的误差阶数为2，与耦合算法的误差阶数一致，两种算法都能得到与本文分析理论相对应的结果。

在上述两个算例中，分别采用解耦有限元算法和耦合自适应有限元算法对模型进行了计算，结果是合理的。通过比较解耦有限元算法和耦合自适应有限元算法在每个网格内的迭代次数，发现两种计算方法的差异，计算结果如表7 所示。

表7 迭代次数比较

通过对比，得出解耦自适应有限元算法在迭代次数和计算时间上明显优于耦合自适应有限元算法，在计算精度和时间上明显优于耦合自适应有限元算法，值得进行推广。

4 结论

本文针对H(curl)空间中的椭圆最优控制问题，建立了一个最优控制系统来解决该问题。然后，进行了有限元逼近的误差分析，研究了其稳定性和收敛性。为了求解偏微分方程最优系统，我们提出了一种自适应有限元方法，通过耦合和解耦两种方式进行求解，所得数值解误差阶与理论分析结果接近。解耦自适应有限元方法在精度和效率上稍有优势，可以推广应用于更复杂的最优控制模型。