针对高温合金微观组织-拉伸性能关系的机器学习预测模型

刘芳宁，王 越，孙瑞侠

(中国航发北京航空材料研究院，北京 100095)

1 前 言

镍基高温合金K4169在-253～700 ℃温度范围内有良好的综合性能，被广泛应用于航空航天领域，用于工作温度一般不高于650 ℃的压气机盘、涡轮盘和叶片等高温合金铸件[1]。K4169合金的强度、疲劳应力等性能由微观组织直接决定[2]，其组成相包括基体相γ相、球状的γ′相、薄片状的γ″相、圆形岛状的Laves相和针或盘状的δ相[3]，其中体心正方结构的γ″相是主要强化相，但其稳定性差，在高温下分解为δ相和γ′相；γ′相是面心立方结构，是合金的辅助强化相；δ相出现在γ基体中时显著降低合金的强度；Laves相是合金的有害相，在晶界及枝晶间处大量析出，呈白色块状。Laves相作为K4169中的一种脆性相，在应力作用下成为裂纹源和扩散通道，显著降低合金的高温性能。碳化物则作为夹杂物常存在于合金中[4]。如果能够掌握合金微观组织与性能间的关系规律，就能够通过控制合金相析出和溶解，来提高组织均匀性，从而进一步提升合金的力学性能和稳定性，获得满足不同强度级别和使用要求的各种零件。对K4169合金微观组织与性能之间关系的研究，常规的方法有实验测量和模拟仿真[5]。但由于K4169合金的微观组织与性能之间没有明确的线性逻辑关系，因此无法通过模拟仿真建立；而实验测量成本高，耗时长，且实验结果难以控制，同样不适用于研究合金微观组织与性能之间的定量关系。

2011年美国提出“材料基因组计划(materials genome initiative, MGI)”，强调通过高通量技术、计算模拟和机器学习等方法，加速新材料的制备，使得材料的开发速度比原先至少提高一倍[6]。机器学习能够根据已有数据，在大量、高维度样本中通过算法学习快速建立特征与相关因素之间的关系，并不断更新和优化以提高模型准确性。机器学习的实用性在于，几乎不需要有关研究对象的先验知识，并且可以从经验数据中准确学习控制性能变化的规则。机器学习的编程范式如图1所示[7]，利用机器学习，人们输入的是数据和从这些数据中预期得到的答案，系统输出的是规则。

图1 机器学习的编程范式[7]Fig.1 Programming paradigm of Machine Learning[7]

将机器学习的方法运用到材料特性的预测中，能够加速新材料的研发设计并降低成本，同时充分挖掘已有数据的价值，在此方面材料信息学已有大量研究并取得显著成果[8-10]。这些研究成果涉及的主要材料类别有：金属材料[11, 12]、非金属材料[13, 14]、陶瓷材料[15]、热电材料[16]等。针对不同的研究对象和具体问题，应选择不同的机器学习方法，典型的机器学习方法有：线性和非线性分析、决策树理论、遗传算法、人工神经网络等。另外，材料描述符的选择和特征维度的控制也是机器学习对材料性能预测是否准确的关键因素。Liu等[17]提出了一种数据驱动的多层特征选择方法，该方法结合了名为DML-FSdek的领域专家知识，无需手动调整超参数即可输入训练数据。他们对10个材料属性数据集的测试研究表明，该方法可以自动搜索比初始特征集具有更低均方根误差的特征集。

根据分析的规模，机器学习在材料特性预测中的应用可以分为宏观性能预测和微观特性预测两大类。对材料的宏观性能研究主要集中在宏观性能与微结构之间的关系。多层感知器(multi-layer perceptron, MLP)，又叫人工神经网络，本质上是一种非线性的统计分析技术，具有很强的自学习、自适应能力，目前广泛应用于材料性能预测、加速模拟计算和辅助材料表征中。例如，Fu等[18]采用MLP、随机森林(random forest, RF)、支持向量机(support vector machine, SVM)和梯度增强算法(gradient boosting，GB)分别预测了蠕变条件(温度、外加应力和时间)对DZ125合金γ′相体积分数、γ′相筏化程度、γ′相厚度等微观组织退化的影响，结果表明，MLP预测结果误差最小，预测准确性最好。Liu等[19]建立了基于分治法的用于预测单晶高温合金蠕变性能的机器学习模型，该算法能够有效区分不同类别的高温合金，并选择最优模型进行进一步预测。该方法比实验更快，成本更低，能够为蠕变断裂寿命建立准确的结构-特性关系映射，并有望用于合金的逆向设计。机器学习对材料微观特性的预测包括预测材料的晶格常数、能带、电子亲和力和分子雾化能等。Jiang等[20]基于SVM、序列最小优化、MLP等机器学习算法，建立化学成分、温度等错配度敏感特征与晶格错配度的关系模型，并从实验与机理两方面对模型进行有效性检验，实现镍基单晶高温合金γ′相和γ相晶格错配度的准确快速预测。结果表明，MLP模型相关系数高，误差低，和传统经验公式相比，预测准确性和效率更有优势。

本研究通过设计实验，突破了K4169标准成分和热处理工艺范围，通过改变合金成分和热处理制度，获取了不同组合变化下对应的微观组织和性能数据。分析了成分和热处理制度变化对合金室温、高温力学性能的影响，并采用机器学习算法建立预测模型，预测了微观组织变化对合金力学性能的影响，为合金微观组织和性能之间的关系提供定量分析方法，加速新材料的研发过程，为合金优化提供指导。

2 实 验

2.1 整体框架

本研究的整体框架如图2所示，首先，设计不同的成分和热处理制度并开展合金熔炼和微观组织观察，获得对应的微观组织金相照片和SEM照片，对照片中的析出相进行统计计算以获得相含量，通过拉伸实验获得不同相含量对应的拉伸性能数据；其次，采用随机化和归一化方法对合金微观组织特征数据和拉伸性能数据进行预处理，为模型的建立做准备；再次，通过支持向量回归(support vector regression, SVR)、随机森林回归(random forest regression, RFR)、K-最近邻回归(K-nearest neighbor node regression, KNR)和MLP[21]这4种算法建立合金微观组织和室温、高温拉伸性能的关系。采用K折交叉验证对预测的准确性进行验证，采用均方误差(mean square error,MSE)、平均绝对误差(mean absolute error,MAE)、相关系数(correlation coefficient,CC)、决定系数(R2)对结果进行评估。MSE和MAE值越小，预测的结果越准确；CC值和R2值越大，预测结果与实际结果越接近，模型的准确性越高。最后，根据误差评估结果选取最优模型作为高温合金微观组织-拉伸性能之间关系的机器学习预测模型。

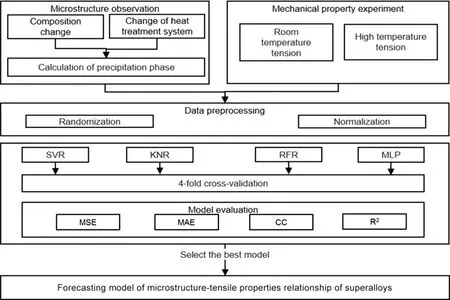
图2 整体框架Fig.2 Overall framework of this study

2.2 实验设计

为了提高镍基高温合金的高温强度，通常会基于固溶强化、第二相强化、晶界强化等综合效果对合金进行成分优化。其中，Al，Ti，Nb是沉淀强化元素，其含量对合金高温时的组织稳定性有重要影响；而Mo能够减慢Al，Ti，Cr元素的高温扩散速率，减缓合金的软化速率，有效提高合金的高温强度。因此，本实验设计了7组成分(表1)并据此熔炼铸锭。其中，第一组取K4169合金标准范围内成分，第二组和第三组是在标准成分基础上改变了Al含量，第四组和第五组改变了Mo含量，第六组和第七组改变了Nb含量。

表1 7组合金名义成分

实验以标准热处理制度为基础，分别设计了10种热处理制度，考察合金微观组织在不同热处理阶段的变化。高温合金K4169常见的标准热处理制度为：1095 ℃/1～2 h(空冷或更快冷)+955 ℃/h(空冷)+720 ℃/8 h(炉冷)至620 ℃，保温8 h(空冷)[22]。设计的包括该热处理制度在内的10组参数见表2。

表2 本实验采用的热处理制度

基于上述成分和热处理制度进行正交实验，综合利用金相显微镜、扫描电镜和透射电镜观察样品，并采用X射线衍射(X-ray diffraction, XRD)对样品不同阶段的微观组织进行表征，计算获得不同相的体积分数，主要关注的微观组织特征数据有γ相、γ′相、γ″相、δ相、Laves相、碳化物等，这些数据即为模型的输入数据；同时通过拉伸实验收集测量的试样室温和600，650 ℃高温拉伸性能数据，本实验采用室温拉伸数据作为建立合金微观组织与室温力学性能关系模型的输出数据，采用600 ℃的拉伸性能数据作为建立合金微观组织与高温力学性能关系模型的输出数据。

2.3 机器学习

机器学习研究的问题分为分类问题和回归问题，分类问题输出的是所属的类别，回归问题输出的是具体值，回归模型是在分类问题的基础上演化而来的。本实验通过建立K4169合金微观组织与力学性能之间的定量关系，从而建立预测模型，因此研究的问题为回归问题。

目前应用广泛的机器学习回归模型有SVR、RFR、KNR和MLP等，其中SVR的优化目标是结构化风险最小，不同于其他算法以经验风险最小为判断依据，因此具有更优秀的泛化能力，SVR的核函数提供了从输入空间到高维空间的映射，降低了算法的复杂度，优化了回归过程；RFR有较强的抗过拟合能力，且非常稳定，只有在半数以上的基分类器出现差错时才会做出错误的预判；KNR算法训练时间复杂度比SVR之类的算法低，与朴素贝叶斯算法相比，对数据没有假设，且对异常点不敏感；MLP是一种对高度非线性数据关系进行建模的神经网络，不需要事先对数据分布进行假设，并且应用到新数据时预测准确性良好。

2.3.1 数据预处理

在机器学习中，数据预处理在训练模型之前是必要的过程。为了保证模型预测结果的准确性，在数据的预处理阶段，首先，将数据进行随机排序；其次，数据的离散化和规范化作为预处理过程中的常见和关键过程，可以减少极端值和异常值的影响，使模型更稳定。本数据集包含的数据本身为数值型，数据本身符合离散化标准，对数据的规范化方式为Z-score规范化，经过处理的数据的均值为0，标准差为1。转化公式见式(1)：

(1)

2.3.2 建立室温拉伸力学性能模型

本实验中SVR、RFR、KNR算法模型的构建基于Python语言中的Scikit-learn算法包[23]完成，MLP基于Python语言中的Keras人工神经网络库完成。

(1)SVR对室温力学性能的预测

本实验中，对合金室温力学性能的预测分别采用了SVR算法的线性核函数(linear)、多项式核函数(polynomial)、径向基核函数(radial basis function, RBF)建立模型，预测结果如图3所示，图中水平轴为实测值，垂直轴为预测值，截距为0、斜率为1的直线为理想直线，图中散点离该线越近，则说明预测的室温力学性能与测量值的一致性越高。从图3中可以看出，线性核函数的预测模型准确性较好，径向基核函数次之，多项式核函数的模型预测结果较差。

图3 K4169合金室温拉伸强度的支持向量回归(SVR)算法预测结果和实验数据对比：(a) 线性核函数，(b) 多项式核函数，(c) 径向基核函数(RBF)Fig.3 Comparison between the predicted results by SVR algorithm and the experimental data of tensile strength of K4169 alloy at room temperature: (a) linear, (b) polynomial, (c) RBF

(2) RFR对室温力学性能的预测

RFR算法中，并不是所有节点都参与当前节点属性指标的计算，影响预测结果的主要参数是树棵数k的选择，本实验中k值设为10，图4为预测结果。从图4中可以看出，该算法的预测结果基本沿对角线分布，说明预测值和实验结果基本吻合。

图4 K4169合金室温拉伸强度的随机森林回归(RFR)算法预测结果和实验数据对比Fig.4 Comparison between the predicted results by RFR algorithm and the experimental data of tensile strength of K4169 alloy at room temperature

(3) KNR对室温力学性能的预测

影响KNR预测模型准确度的重要指标是近邻个数k，本实验将k的取值分别设置为1～6，计算其预测结果与实际实验结果的MSE、MAE、CC及R2，结果如表3所示。结果表明，k=6时的误差最小，相关系数最高，此时的预测结果见图5，从图中可以看出，该算法的预测结果基本沿对角线分布，说明预测值和实验结果基本吻合。为保证观测点的近邻比远处的邻近点具有更大的影响力，每个邻近点的权值设置为与观测点距离的倒数，此处距离为欧拉距离。

图5 K4169合金室温拉伸强度的K-最近邻回归(KNR)算法预测结果和实验数据对比Fig.5 Comparison between the predicted results by KNR algorithm and the experimental data of tensile strength of K4169 alloy at room temperature

(4) MLP对室温力学性能的预测

通过调整层数和节点数，确定了MLP对KCH69室温力学性能预测的模型的过拟合临界点参数。实验表明，MLP的室温力学模型的最佳参数为：层数为3层，第一层和第二层节点数为64，第三层节点数为1，激活函数为Relu时，模型预测的准确性最好，此时模型的MSE值为0.17，MAE值为0.32，CC值为0.95，R2值为0.85。预测结果见图6，从图中可以看出，该算法的预测结果基本沿对角线分布，说明预测值和实验结果基本吻合。

图6 K4169合金室温拉伸强度的多层感知器(MLP)算法预测结果和实验数据对比Fig.6 Comparison between the predicted results by MLP algorithm and the experimental data of tensile strength of K4169 alloy at room temperature

为了减小模型预测中过拟合情况的出现，在模型训练过程中，采用了k折交叉验证来避免偶然性。交叉验证作为一种模型验证技术，可用于评估统计分析结果推广到独立的数据集时该算法的预测效果。将本实验中的数据分为训练集、验证集和测试集3类。首先留出所有数据集的1/5为测试集，剩余数据为训练集和验证集，其划分方法为：设D为训练集，将D分为4个互斥的分区D1、D2、D3和D4，随机有17或18个实例。回归算法执行10次，每次使用3个分区进行训练，留下1个分区进行验证。通过10次重复的四折交叉验证对模型进行分析和验证。

2.3.3 建立高温拉伸力学性能模型

对高温拉伸性能的预测采用同样的算法SVR、KNR、RFR和MLP，每种算法执行10次，评估结果取10次执行结果的平均值。4种算法预测结果与真实实验数据的对比如图7所示。从图中可以看出，相比于其余3种模型，MLP算法的预测结果命中对角线的次数较高。

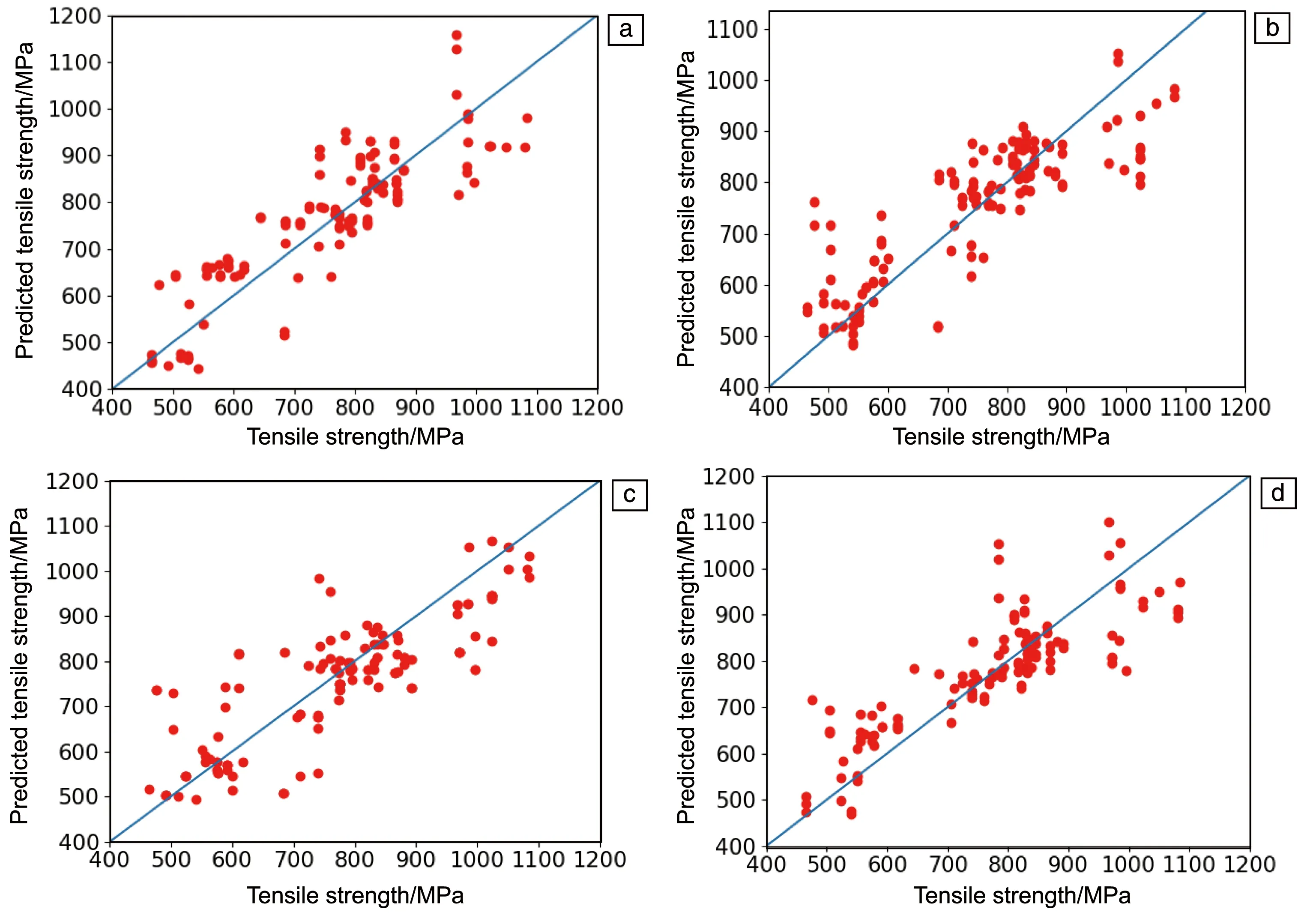
图7 K4169合金高温拉伸强度的不同算法预测结果和实验数据对比：(a) 支持向量回归(SVR)，(b) 随机森林回归(RFR)，(c) K-最近邻回归(KNR)，(d) 多层感知器(MLP)Fig.7 Comparison between the predicted results by different algorithms and the experimental data of tensile strength of K4169 alloy at high temperature: (a) SVR，(b) RFR，(c) KNR，(d) MLP

3 结果与讨论

3.1 对拉伸实验结果的分析

图8是不同成分合金在不同热处理制度处理后的室温和600，650 ℃拉伸强度。从图8中可以看出，同一成分的合金在不同热处理状态下的室温拉伸强度均高于其高温拉伸强度，相同热处理制度处理后的合金强度值在600与650 ℃下差异很小，表现出较好的高温稳定性。

图8 不同成分合金在不同热处理制度处理后的拉伸强度：(a)室温，(b)600 ℃，(c)650 ℃Fig.8 Tensile strength of alloys with different compositions after different heat treatment treatments: (a) room temperature, (b) 600 ℃, (c) 650 ℃

3.2 对机器学习预测结果的分析

图9显示了4种算法建立的模型的室温拉伸强度预测值和实测值的MSE、MAE、CC以及R2值对比，从图9a和9b中可以看出，与其余3种模型相比，MLP模型的MSE和MAE均为最低；从图9c和9d中可以看出，MLP模型的CC和R2最高，因此选取该算法为根据相含量预测室温拉伸强度的最优算法，该算法的MSE为0.17，MAE为0.32，CC为0.95，R2为0.85。

图9 不同算法对合金室温拉伸强度预测的误差评估结果：(a) 均方误差，(b) 平均绝对误差，(c) 相关系数，(d) 决定系数Fig.9 Comparison of error evaluation results of predicting tensile strength of alloy at room temperature by different algorithms: (a) MSE, (b) MAE, (b) CC, (d) R2

对4种模型的600 ℃高温拉伸强度预测结果的定量化误差分析结果见图10。从图10a和10b中可以看出，MLP模型的MSE和MAE均为最低；从图10c和10d中可以看出，与其余4种算法相比，MLP算法的CC和R2最高，因此选取该算法为根据相含量预测600 ℃高温拉伸强度的最优算法，该算法的MSE为0.14，MAE为0.29，CC为0.97，R2为0.91。

图10 不同算法对合金高温拉伸强度预测的误差评估结果：(a) 均方误差，(b) 平均绝对误差，(c) 相关系数，(d) 决定系数Fig.10 Comparison of error evaluation results of predicting tensile strength of alloy at high temperature by different algorithms: (a) MSE, (b) MAE, (b) CC, (d) R2

4 结 论

本研究以高温合金K4169为基础，设计并制备了不同成分和热处理制度处理后的高温合金铸件，观测并计算微观组织中的相含量，并对不同铸件的室温拉伸强度和600、650 ℃高温拉伸强度进行测量，获取了相含量和力学性能的数据。合金室温和高温拉伸性能实验结果表明，成分一定时，合金的室温拉伸强度整体高于高温拉伸强度；600与650 ℃下拉伸强度差异很小，表现出较好的高温稳定性。

采用支持向量回归(support vector machine regression, SVR)、随机森林回归(random forest regression, RFR)、K-最近邻回归(K-nearest neighbor node regression, KNR)和多层感知器(multi-layer perceptron, MLP)这4种机器学习的回归预测模型，确定最佳参数，建立相含量与室温拉伸、高温拉伸力学性能的关系。对4种模型的预测值误差分析表明，MLP的预测准确性最高。本实验证明，根据材料的成分、工艺、微观组织、性能等信息, 采用机器学习的方法建立关系模型，可为合金微观组织与性能之间的关系提供定量的分析方法，并实现对材料性能的预测。与普通机器学习算法相比，以MLP算法为代表的深度学习预测模型对材料性能的预测准确性更高，若将它应用到材料性能实验中，可有效加速材料的试制过程, 为材料设计及新材料的研发提供辅助和指导。此外，机器学习中模型的准确性和训练数据的数据量有较大关系，后续研究中将收集更多的数据，并补充到数据集中，以提高模型的准确性。