结合流形滤波的矩阵信息几何检测器*

华小强，程永强，王宏强，王勇献，张理论

(1. 国防科技大学 气象海洋学院， 湖南 长沙 410073； 2. 国防科技大学 电子科学学院， 湖南 长沙 410073)

信号检测是雷达、声呐、通信等领域的基本问题，通常，信号检测的性能与背景杂波协方差矩阵的估计性能紧密相关，杂波协方差矩阵的估计精度越高，检测性能越好。在实际应用中，检测背景常呈现较强的非均匀特性，极大地限制了协方差矩阵的估计性能，为信号检测带来了巨大的挑战。一方面，能用来估计杂波协方差矩阵的均匀样本数较少，研究表明，当样本数大于等于数据维数的2倍时，检测性能损失小于3 dB，而当样本数小于2倍的数据维数时，信号检测性能存在较大的损失；另一方面，用来估计杂波协方差矩阵的样本中不可避免地存在干扰，使得协方差矩阵估计的稳健性下降，严重影响了信号检测的性能。小样本、非均匀杂波下的信号检测是一个难点问题，亟须提升信号检测的性能。

为了提升小样本、非均匀杂波下的信号检测性能，通常有两类方法：一类是利用背景杂波或结构矩阵的先验信息来提升协方差矩阵的估计精度或鲁棒性，如文献[1]假设干扰服从多通道自回归(autoregressive, AR)模型，并以此设计了两种检测器，仿真实验验证了检测性能在小样本条件下的优势；文献[2]设计了一种鲁棒的对称泰勒M估计器，该估计器对干扰具有较好的鲁棒性；文献[3]假设杂波协方差矩阵具有Kronecker结构，根据此结构分析了信杂比(signal-to-clutter-noise ratio, SCNR)的损失和检测性能提升的情况，并依据实验验证了此结构的优势。类似的方法还有假设矩阵具有托普利兹结构、低秩结构等[4-6]，这类方法能取得性能提升的关键是获取合适的杂波先验信息，然而，在实际应用中很难获得杂波环境的统计特性等先验信息，极大限制了此类方法的实用性。另一类方法不需要依据杂波协方差矩阵的统计特性等先验信息，将样本的相关性数据建模为一个托普利兹正定矩阵，在矩阵流形上度量目标信号与杂波对应矩阵间的区分性，以此实现信号检测。这类方法以矩阵信息几何理论为基础，利用流形局部几何结构的差异性来衡量目标与杂波间的区别，因此称为矩阵信息几何检测器，主要有黎曼均值检测器[7]、信息散度检测器[8-13]等，该类检测器已成功应用于飞机尾流检测[14]、X波段雷达目标检测[15]以及非高斯杂波下的信号检测[16-18]，并被证明具有一定的性能优势。该类方法的性能和目标与杂波间的区分性、模型结构、数据特征等因素有关。

基于矩阵信息几何检测器的思想，本文提出一种流形滤波方法来提升目标与杂波间的区分性，将每一个样本的相关性数据建模为一个正定矩阵，在矩阵流形上，利用样本矩阵周围的若干矩阵进行流形滤波，去除部分杂波信息。具体地，利用邻近矩阵的加权几何均值来代替矩阵，类似于欧氏空间中的平滑滤波思想，增强目标与杂波间的区分性，提高信杂比。在此基础上，计算辅助样本数据对应矩阵的几何均值，比较待检测样本矩阵与几何均值间的距离和检测门限之间的大小，以实现对是否存在目标的判决。仿真实验证明，相比于自适应匹配滤波(adaptive matched filter, AMF)和未进行流形滤波的几何检测器，该检测方法在小样本、非均匀杂波下具有明显的性能优势。

1 矩阵信息几何理论的基本知识

矩阵信息几何[19]是在矩阵流形上采用微分几何方法来研究矩阵类数据的信息处理问题的一门学科，是信息几何理论[20-25]在实际应用中发展较快的一套理论体系，信息科学中的许多问题，如分类、参数估计等，都可以与矩阵流形的几何结构建立起联系，从而将信息处理问题转化为矩阵流形上的几何问题来研究，将问题几何化，通过解决几何问题来完成信息处理问题。目前，矩阵信息几何理论一方面正在完善其理论体系，另一方面扩展其应用，在信息科学领域取得的一些成果都具有一定的开创性。下面将介绍与本文相关的一些矩阵信息几何理论的基本概念，即Hermitian正定矩阵流形、几何度量及其均值。

1.1 Hermitian正定矩阵流形的几何

矩阵流形是矩阵信息几何的研究基础，对于一个n阶复矩阵A∈n×n，如果AH=A，则A为Hermitian矩阵，所有的n×n阶Hermitian矩阵构成集合Hn，即

Hn={A|A=AH}

(1)

对于矩阵A∈n×n，如果∀x∈n且x≠0，二次型都满足xHAx>0，则称矩阵A为正定矩阵，记为A0。如果矩阵A满足A∈Hn且A0，则称矩阵A为Hermitian正定矩阵，所有的n×n阶Hermitian正定矩阵构成集合即

(2)

(3)

其中，tr(·)表示矩阵的迹。相应的范数可定义为

(4)

[0,1]

(5)

基于式(5)的测地线，可计算R1和R2间中点，即均值G(R1,R2)：

(6)

G(R1,R2)表示连接R1和R2的测地线的中点，即到点R1和R2的距离相等的点。

1.2 矩阵流形上的度量及其均值

在矩阵流形上，度量两点间距离的方法很多，不同的度量方法反映了流形不同的几何结构，所度量出的差异性也不同。常用的度量方法有AIRM、对数欧几里得度量(log-Euclidean metric, LEM)、对称库尔贝克-莱布勒散度(symmetric Kullback-Leibler divergence, SKLD)以及詹森-布雷格曼洛格德特散度(Jensen-Bregman LogDet divergence, JBLD)，这四种度量均满足对称性，即距离函数满足δ(A,B)=δ(B,A)。其中，AIRM和LEM是测地线距离，满足距离的性质；AIRM、SKLD和JBLD具有仿射不变性，即对于可逆矩阵M∈n×n，δ(MHAM,MHBM)=δ(A,B)。四种距离度量的定义如下：

(7)

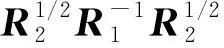
(8)

(9)

其中，I表示单位矩阵。

(10)

不同的几何度量确定了流形的不同几何结构，在流形上利用不同的几何度量所度量出两点间的差异性不同，选取合适的几何度量，可以得到较好的区分性。此外，基于不同的几何度量，可以得到不同的几何均值。

对于一组实数xi∈,i=1,2,…,K，其均值为K个数之和的平均，即实质上，代数均值是到K个数的距离平方和最小的值，可以表示为如下的优化问题：

(11)

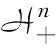
(12)

其中，αi是第i个矩阵对应的权值，d(·,·)表示两矩阵间的几何距离。

利用不同的几何距离，可得到不同的几何均值，四种几何均值由以下推论给出。

推论1对于矩阵集{R1,R2,…,RK}，其对应的AIRM均值由以下迭代式给出：

(13)

推论2对于矩阵集{R1,R2,…,RK}，其对应的LEM均值由下式给出：

(14)

推论3对于矩阵集{R1,R2,…,RK}，其对应的SKLD均值由下式给出：

(15)

推论4对于矩阵集{R1,R2,…,RK}，其对应的JBLD均值由下式给出：

(16)

上述推论中，下标t表示迭代次数，εt表示迭代步长。

2 基于流形滤波的几何检测器

基于流形滤波的几何检测器的基本思想是将样本的相关性数据建模为一个正定矩阵，在矩阵流形上通过滤波处理去除部分杂波信息，并利用局部几何结构的差异性来区分目标与杂波，从而实现信号检测。下面首先介绍流形滤波的基本原理，然后介绍基于流形滤波的几何检测原理。

2.1 流形滤波的基本原理

(17)

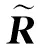
(18)

对于不同的几何距离，滤波后的矩阵都不一样。 对于权值wi，通常要求其满足以下约束：

(19)

权值wi需考虑两矩阵在流形上的差异性，本文取指数函数来定义相似性权值，并考虑归一化，权值wi可定义为

(20)

在上述的滤波中，m和h是自由参数，m表示用来滤波的矩阵数目，m越大，用来滤波的矩阵数越多，滤波效果越好；h表示滤波控制参数，h越大，滤波矩阵的权值差异性越小，滤波效果越接近等权值的均值，滤波效果越差。

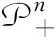
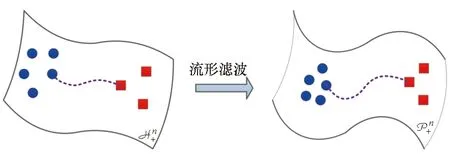
图1 流形滤波前后杂波与目标信号间的区分性Fig.1 Discrimination between clutter and target signal before and after manifold filter

2.2 基于流形滤波的几何检测原理

基于流形滤波的几何检测器首先将样本数据的相关性建模为正定矩阵，在矩阵流形上利用每个矩阵的邻近矩阵进行加权滤波以去除部分杂波信息，提升杂波与目标间的区分性；然后，计算辅助样本对应矩阵集的几何均值，比较待检测样本矩阵与几何均值间的距离和检测门限之间的大小，从而实现信号检测，其检测原理如图2所示。

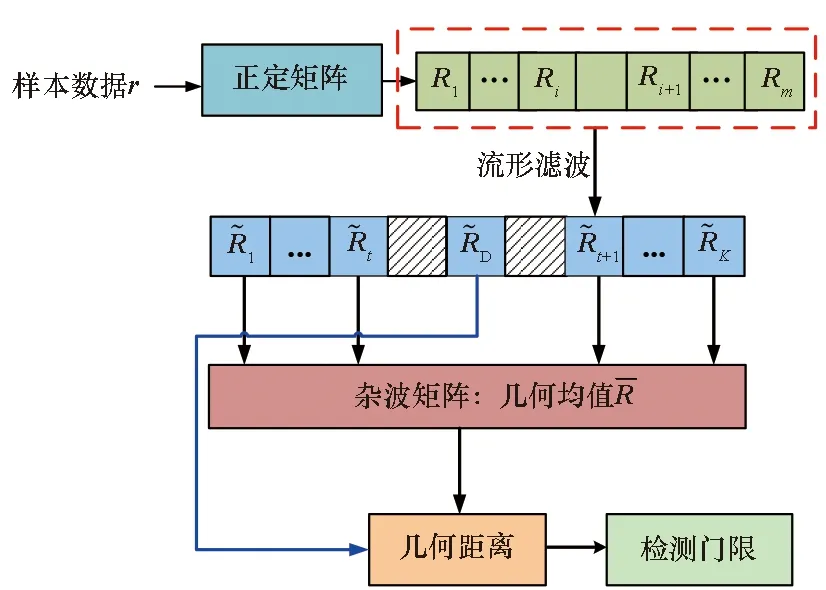
图2 基于流形滤波的几何检测原理Fig.2 Principle of geometric detectors based on manifold filter

对于样本数据r=[r0,r1,…,rn-1]T，其相关性可通过建立AR模型来获取，样本数据r的相关性矩阵可表示为

(21)

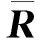
(22)

其中，H0和H1分别表示只有杂波和含有目标信号的假设，γ是检测门限。

3 仿真分析

为了验证本文方法的有效性，通过仿真实验来分析几何均值的鲁棒性、流形滤波前后的区分性变化以及检测性能的优势，并与自适应检测器进行比较。

3.1 几何均值的鲁棒性分析

为了验证几何均值对干扰的鲁棒性，仿真产生40个服从均值为0、协方差矩阵为Σ的高斯分布的样本数据，协方差矩阵Σ由式(23)计算得到。

(23)

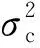
(24)

图3给出了不同干扰数对几何均值的影响，从结果可以看出，干扰数对样本协方差矩阵(sample covariance matrix, SCM)的影响最大，其误差曲线的斜率最大，而干扰数对几何均值的影响较小，其中，干扰数对JBLD均值的影响最小，AIRM和LEM均值的误差接近，SKLD均值的误差最大。这说明，几何均值对干扰数的鲁棒性强于SCM，在四种几何均值中，JBLD均值的鲁棒性最好，SKLD均值的鲁棒性最差，而AIRM和LEM的鲁棒性接近。

图3 不同干扰数对几何均值的影响Fig.3 Influence of different number of interferences on geometric means

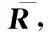
(25)

图4给出了不同样本数对杂波矩阵估计性能的影响，从结果可以看出，在不同样本数下，SCM的误差比几何均值的误差大，这说明，利用几何均值进行杂波矩阵估计，其估计性能受样本数的影响较小。在四种几何均值中，SKLD均值的误差最小，而AIRM均值、LEM均值和JBLD均值的误差比较接近，这说明利用SKLD均值作为杂波矩阵，其估计性能受样本数的影响最小，而AIRM均值、LEM均值和JBLD均值受样本数的影响比较接近。

图4 不同样本数对杂波矩阵估计性能的影响Fig.4 Influence of different number of sample on the performance of clutter matrix estimation

上述实验分别验证了几何均值对不同干扰数的鲁棒性以及不同样本数对几何均值的估计性能影响，实验结果说明，几何均值对干扰数的鲁棒性强于SCM，其中，JBLD均值的鲁棒性最好，其次是AIRM和LEM均值，SKLD均值的鲁棒性是四种几何均值中最差的。同时，利用几何均值进行杂波矩阵估计的性能受样本数的影响小于SCM，其中，SKLD均值受样本数的影响最小。这些结果充分验证了几何均值对干扰数和样本数的鲁棒性。

3.2 目标与杂波间的区分性分析

为了验证流形滤波前后目标与杂波间的区分性变化情况，仿真产生40个样本数据，在第20个样本数据中加入信杂比为20 dB的信号，将每一个样本数据建模为一个正定矩阵，对每一个样本矩阵，利用其左右各5个样本矩阵计算几何均值，然后，计算每个样本矩阵与其对应几何均值矩阵之间的几何距离，并将其归一化，得到归一化检测统计量。

图5给出了不同几何均值检测器的归一化统计量结果，其中，AIRM、LEM、SKLD、JBLD以及WAIRM、WLEM、WSKLD、WJBLD分别是流形滤波前后的检测器。从结果可以看出，滤波后，杂波的归一化检测统计量相对变小，这说明，杂波与杂波之间的距离变得更小。此外，目标处的归一化检测统计量为1，相对于杂波的归一化检测统计量来说，滤波后，目标与杂波间的距离变得更大。这也说明，滤波后，杂波与杂波相距更近，而目标与杂波相距更远，目标与杂波间的区分能力变强，信杂比提升。

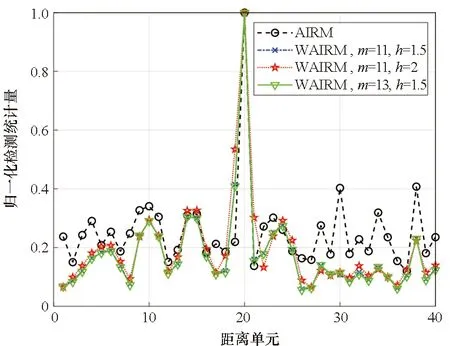
(a) AIRM均值(a) AIRM mean

为了进一步分析目标信号与杂波间的区分性，利用流形上的局部几何结构描述方法，即各向异性因子。对于流形上的任一点P，其各向异性因子定义为

(26)

各向异性因子A(P)描述了矩阵流形上点P处的局部各向异性，不同位置处的各向异性不同，各向异性因子的大小与所利用的几何距离度量方法有关。对于矩阵流形上两点间的局部几何结构的差异，考虑到不同度量方法带来的量纲差异，利用式(27)来定义矩阵流形上两点P1和P2间的区分能力描述子：

(27)

式(27)定义的区分能力通过两各向异性因子之商，可以消除量纲的影响，同时，假设点P1表示含目标信号，点P2只包含杂波，则两点间的区分能力描述子L(P1,P2)越大，P1和P2之间的区分性越好。仿真产生了100组样本数据，每组样本数据包含13个样本，在第13个样本数据中加入信杂比为20 dB的目标信号，利用前12个样本数据对应的矩阵计算几何均值，计算两矩阵间的区分能力描述子L(P1,P2)，结果如图6所示。

图6 不同几何度量在滤波前后的区分能力Fig.6 Discrimination ability of different geometric measures before and after manifold filter

从图6的结果可以看出，流形滤波之后，目标与杂波间的区分能力描述子的值变大，这说明，目标与杂波间的区分性变强，这进一步验证了本文算法的有效性。

3.3 检测性能分析

为了验证基于流形滤波的几何检测器的性能优势，分别在高斯和非高斯杂波下仿真产生1 000组样本数据，每组样本数据中包含K个仅含杂波的辅助数据和1个含有目标信号的样本数据，样本数据的维数为n，在实验中，取n=8。计算辅助数据对应矩阵的几何均值，然后计算目标样本数据对应矩阵与几何均值间的几何距离，并与检测门限进行对比，分别给出K=n和K=1.5n条件下不同几何检测器的检测性能曲线，如图7～10所示。

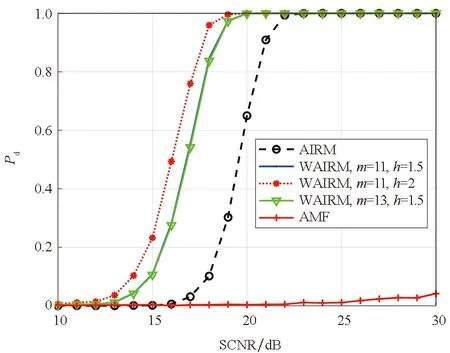
(a) 高斯杂波，K=n(a) Gaussian clutter，K=n

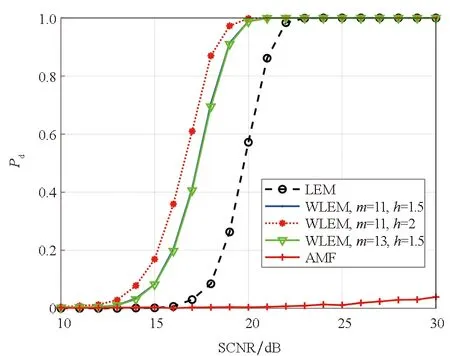
(a) 高斯杂波，K=n(a) Gaussian clutter，K=n

(a) 高斯杂波，K=n(a) Gaussian clutter，K=n

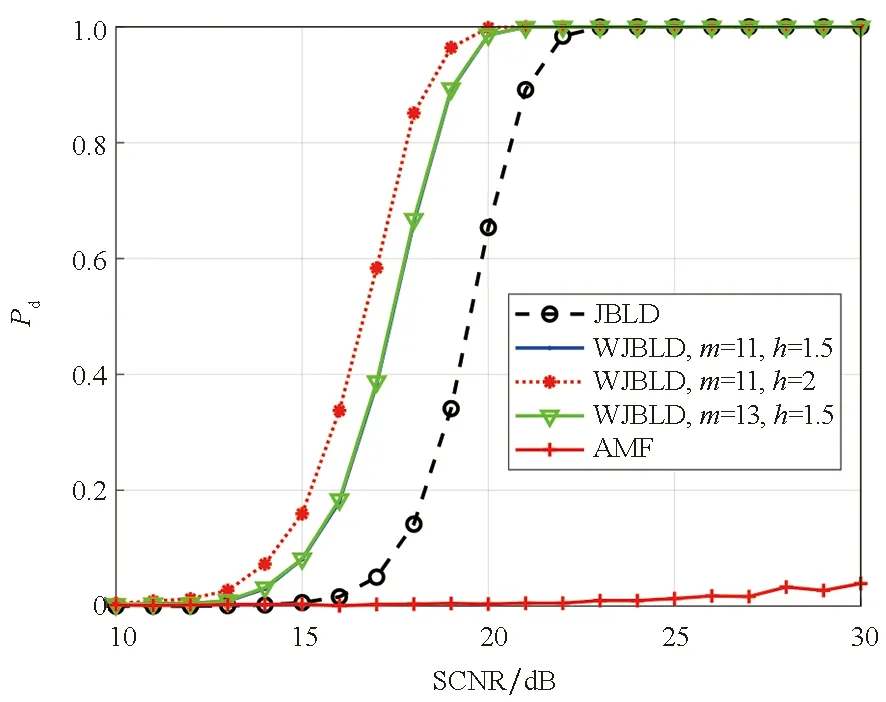
(a) 高斯杂波，K=n(a) Gaussian clutter，K=n

从图中结果可以看出，当K=n时，由于利用SCM进行杂波协方差矩阵的估计性能较差，AMF算法基本失效，而几何检测器的性能较好，滤波后的检测器性能均优于未滤波的几何检测器。当K=1.5n时，几何检测器的性能同样优于AMF的性能。此外，可以看出，随着辅助样本数K的增加，几何检测器的性能变好，并且，高斯杂波下的性能比非高斯杂波下的性能要好，这些结果充分验证了基于流形滤波的几何检测器的性能优势。

4 结论

本文针对小样本、非均匀杂波下的信号检测问题，提出了一种基于流形滤波的矩阵信息几何检测器，该检测器将信号检测问题转化为矩阵流形上的几何问题。该检测方法将样本数据的相关性建模为一个正定矩阵，在矩阵流形上通过加权平滑滤波的方法去除部分杂波信息，增强杂波与目标信号检测的区分性，从而提升信杂比。此外，通过比较待检测样本矩阵与辅助数据对应矩阵的几何均值之间的距离与检测门限的大小以实现信号检测。仿真实验分析表明，几何均值对干扰数和样本数具有较强的鲁棒性，同时，通过流形滤波可使得杂波间的距离更小，而目标信号与杂波间的距离更大，并依据检测性能曲线验证了基于流形滤波的几何检测器的性能优势。