车载多接入边缘网络中联合资源分配和动态任务卸载方案*
2022-12-02薛建彬关向瑞安亚宁
薛建彬,安 悦,关向瑞,安亚宁
(兰州理工大学 计算机与通信学院, 甘肃 兰州 730050)
随着移动网络和物联网技术的快速发展,专家预测:至2022年,汽车产业年销量将达到600万辆,全球汽车电子市场规模达3 800亿美元,继续呈加速增长态势,智能网联车热潮已经袭来[1]。车辆激增涌现出了越来越多的时延敏感型和计算密集型的新型应用,例如自动驾驶、车辆社交网络[2]和交互式游戏[3],为了应对不断激增的数据流量和海量的设备连接,5G将渗透在未来生活的各个领域。车联网技术与5G的落地应用,将为未来无人驾驶汽车提供可靠的技术支持,并将车联网带入一个新时代——无人驾驶时代。但是,这些新型应用给人们的生活带来巨大便利的同时,大量的计算密集型应用会消耗更多的能量,给车载终端造成巨大的压力[4]。此外,由于移动车载终端的计算资源有限,会增加消息处理的时延[5],这对车联网技术的研究产生了巨大的挑战。
面对这些挑战,提出了支持多接入边缘计算(multi-access edge computating,MEC)[6]的车载网络架构。MEC服务器有强大的计算和存储能力[7],基于MEC的解决方案,可以提供低时延、高带宽并切合各应用场景的计算处理能力,具有很强的适用性,在这种协作架构下,车辆产生的任务可以卸载至路边基础设施单元(rode side unit,RSU)上的MEC服务器执行或者卸载至通信范围内的其他车辆上处理,从而节省了传输时延和处理能耗,解决了车辆自身计算资源不足的问题[8]。
针对车辆计算资源不足的问题,建议将车辆任务卸载到其通信范围内的其他车辆执行,考虑到车辆的移动性,在动态网络下定义了一个风险函数来评估任务卸载失败的可能性,并联合系统风险提出了卸载效用函数。
1 相关工作
随着以大数据为主要特征的各种先进技术在交通领域的应用,车联网成为必然的发展趋势。然而现今的车载设备有限的计算和存储能力难以满足大量高计算需求和低时延的限制,因此如何平衡应用时延高要求和车载终端计算能力,成为近些年研究的重点。多接入边缘计算作为5G演进的关键技术,有助于克服车联网领域中的发展瓶颈,为其发展提供有力支持。
针对车辆自身资源不足的问题,Hou等[9]提议将道路空闲车辆作为基础设施,让这些车辆提供卸载所需的计算资源。此外,文献[10]引入了M/M/1排队模型,设计了一种基于MEC负载状态的预测性卸载策略,通过车与车通信方式进行任务卸载。文献[11]不仅考虑将车辆产生的任务卸载至边缘服务器,还进一步把任务划分为可分割和不可分割,再分别进行卸载,以减少系统能耗。
前期研究任务卸载的目的是为了优化终端设备的能耗或者节省任务处理时延,但随着研究的深入,在计算卸载过程中,除了上述优化目标外,还有许多学者研究了卸载过程中的无线电资源分配和计算资源分配[12]。例如,Wang等[13]在考虑系统总收入的条件下,联合优化卸载决策和资源分配,以提高无线网络的性能。此外,车联网络的服务质量和网络成本也值得重点关注。文献[14]提出了一种时延预测的组合方式,将任务自适应地卸载到MEC服务器,节省了计算成本。Si等[15]将车辆视为边缘节点,利用车辆的潜在资源,减轻了网络中的数据拥塞问题,提升了用户的服务质量。
总的来说,大部分已有研究将任务卸载处理可以节省成本[16],或提高用户的卸载效用[17],能够弥补车辆自身资源匮乏的缺点。但这些方案都有一些局限性,以上研究都假设系统是准静态的,并没有考虑到车辆速度过快导致车与车或者车与基础设施通信过程中连接中断的问题[18]。一旦在任务卸载期间车辆或是MEC服务器与产生任务的终端车辆断开连接,将会增大网络时延和能耗成本。因此,为了提高网络性能,在车辆卸载过程中,应考虑到车辆的移动性对系统的影响。
2 系统模型
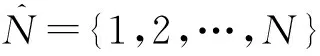
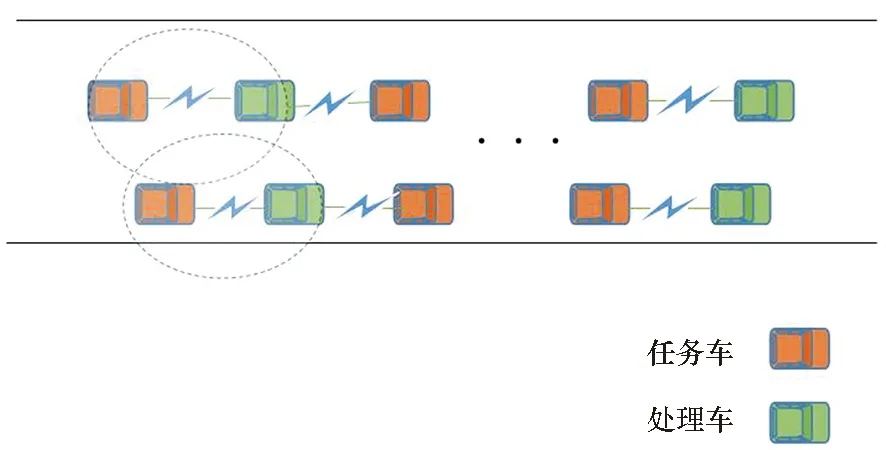
图1 基于V2V通信的计算任务卸载Fig.1 Computing task offloading based on V2V communication
2.1 本地计算任务模型
(1)

(2)
其中,ε为能量系数,它的值取决于芯片结构。
2.2 任务卸载模型
任务节点n卸载它的任务Kn到其中一个处理车辆j,产生的延迟由三部分组成:传输延迟,在处理节点的计算延迟,输出结果回传延迟。但是,由于输出数据远小于输入数据,因此,第三部分的延迟经常可以忽略。

(3)

(4)
其中,hnj为任务车辆n和处理车辆j之间的信道增益,pn为任务车辆n的发射功率,σ2为背景噪声方差。
则上行链路发送任务Kn的时间为:
(5)
任务在处理车辆处花费的时间为:
(6)
(7)
则卸载的总时延为:
(8)
上行链路的能量消耗为:
(9)
2.3 卸载风险模型
定义当卸载时间大于车辆之间连接时间为风险。设计一个风险评估模型来估计车辆卸载失败的可能性,风险被公式化为卸载时间与车辆连接时间的比例。
(10)

2.4 卸载效用模型
定义卸载效用函数为:
(11)

3 问题建模和解耦
3.1 问题建模
对于给定的卸载决策和资源分配,定义系统的卸载效用为所有用户卸载效用的加权和。本节将优化问题公式化为混合整数非线性规划(mixed integer nonlinear programming, MINLP),目标函数为:
(12)
(13)
(14)
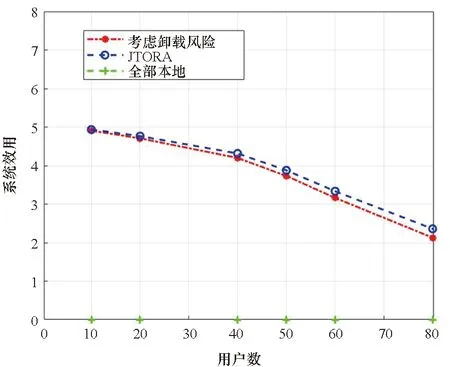
0 (15) (16) (17) 约束式 (13)是一个二进制卸载变量,表示任务可以在本地计算,也可以卸载到处理车辆执行。式(14)表示一个任务至多卸载至一个处理车辆执行,式(15)表示传输功率约束,式(16)表示每个卸载任务都应该分配计算资源,式(17)表示分配的总的计算资源应该在处理车辆的服务能力之内。 给定一个满足约束式(13)、式(14)的任务卸载决策,整理可将目标函数重写为: (18) 对于给定的卸载决策,式(18)中的第一项为常数。 其中 (19) 所以目标变成了 (20) 根据式(8)、式(9)、式(19)。可以得到 (21) 3.2.1 功率分配问题 s.t. 0 (22) s.t. 0 (23) 引理1达到最优值v*的条件是,当且仅当 =0 (24) 该定理的证明可在文献[21]中得到。 上述定理表示问题P1可以通过它的等价问题式 (24)得到。此外,由于v*一般是未知的,故用v代替[22],如算法1所示。 问题式(23)可以改成以下形式: 0 (25) 为了解决P2,注意到问题P2为凸函数和线性函数的加权和,同时约束条件为凸条件,因此问题P2为凸函数[23]。 该问题满足斯莱特条件,可以使用拉格朗日对偶分解和梯度下降法来解决[24]。 利用拉格朗日乘子法可将问题转化为: (26) 该问题可以通过一个主问题和多个子问题的迭代来解决[24]。 子问题为: (27) 拉格朗日函数为: (28) 其中,k=(k1,k2,…,kNoff)≥0。通过KKT(Karush-Kuhn-Tucker)条件,求函数L(p,k)对于pn的微分,可以获得每个用户的最优传输功率分配。 (29) 算法1 迭代功率分配解决P1 主问题通过拉格朗日乘子来解决,利用梯度下降法更新拉格朗日乘子,k的表达式为: (30) 3.2.2 计算资源分配问题 (31) (32) (33) 注意到式(32)~(33)两个约束条件都是凸条件,将目标函数P3用Υ(,Α)来表示。Υ(,Α)关于fnj的二阶导数为: (34) 因此P3是一个凸优化问题,可以用KKT来解决。 (35) Υ( (36) 证明:问题P3的拉格朗日函数为: (37) γ=(γ1,…,γj)是拉格朗日乘子,对fnj求一阶导数,可得: (38) 令式(38)等于0 ,求解出fnj,然后可得到最优的计算资源分配。 (39) (40) (41) 把式(41)代入式(39)可得: (42) 最后,目标函数P3可表示为: Υ( (43) 3.2.3 联合任务卸载调度和资源分配 在上述分析中,对于一个给定的卸载决策,获得了功率分配和计算资源分配,根据式(18)、式(21)和式(36)可得: (44) (45) (46) 其中,p*可以通过算法1 获得,F*可以通过式(35)得到。 原始问题可重写为: (47) 解决问题式(38)的一个直接方法是穷举所有可能的卸载决策,进而得到最优的卸载决策,但此种方法复杂度为Ο(2n),其中n=N×J,显然,使用穷举法是不切实际的,因此提出一种次优卸载决策的方法来降低复杂度[25]。程序初始时,假设卸载集合=∅,找到效用最大的集合,如果存在一个决策anj∈,将它删除后集合的效用比删除之前的集合效用大,那么执行删除操作,从集合中删除这个决策,直到再也找不出这样的决策就停止删除操作;如果存在一个决策anj∈Q/,将该决策加入集合中,使得系统效用的值变大,那么执行交换操作,直到再也找不出这样的决策,程序结束。最后,找到了使系统效用最好的卸载决策集合,具体步骤如算法3所示。 图2(a)~(c)所展示的是用户数和系统效用之间的关系,将用户数逐步增加,并在三种不同工作负载的情况下进行比较。从图2(a)~(c)可以看出,随着任务量的增加,所有方案的性能也显著增加。这是因为,当任务需要更多的计算资源时,用户将从把任务卸载到处理车辆中获益更多。还发现,随着用户数的增加,系统效用也在增加。这是因为,当有许多用户竞争无线资源和计算资源来卸载他们的任务时,发送任务和在处理车辆上执行任务的开销会更高,从而降低了卸载效用。从图中还可以看出,在用户数相同的情况下,本文所提JDTORA方案与联合任务卸载和资源分配(joint task offloading and resource allocation, JTORA)方案的系统效用性能极其接近,差值趋于0 。这说明在考虑卸载风险的情况下,即对影响系统卸载的因素考虑更为全面时,系统效用依旧可以趋于不考虑风险的优解,验证了所提方案的有效性。与传统的全部本地计算方案进行了比较,本地计算时的卸载效用值为0,因此,当用户数相同的情况下,本文所提方案的效用大于本地卸载方案的效用。 (a) cn=1 000 图3(a)~(b)表示当用户对时间的偏好因子从0.1到0.9变化时,用户的平均时间消耗和能量消耗变化趋势。从图中可以看出,当用户对时间的偏好α增加时,平均时间消耗降低,相反,平均能量消耗随之增加。此外,图中显示当用户数更多时,用户会经历更大的时间消耗和能量消耗,这是因为当争夺有限资源的用户数更多时,用户从卸载的任务中获益的机会更小。 (a) 平均时间消耗(a) Average time consumption 图4显示的是用户数与系统风险之间的关系。本文的风险是由于任务卸载引起的,从图中可以直观地看出,当任务不进行卸载时(anj=0),系统风险为0;而当用户数增加时,系统的风险也随之增大。这是因为当更多的用户卸载它们的任务时,增大了系统的卸载风险。 图4 不同工作负载情况下,针对不同用户数的系统风险比较Fig.4 Comparison of system risks with different numbers of users under different workloads 通过卸载决策和资源分配的联合优化,设计了边缘车联网系统中基于考虑卸载风险的效用最大化问题。优化问题被表述为混合整数非线性规划问题,此问题是难以解决的,因此将原始问题解耦成两个子问题,分别使用凸优化技术和分式规划技术解决。最后,联合两个子问题的解在多项式时间内求出了最优的卸载决策。仿真结果表明所提方案在有大量用户车辆的实际环境中是有效的。 与其他研究不同的是,本文考虑到车辆的移动性,设计了联合资源分配的动态任务卸载方案,建模了一个风险函数来评估车辆连接中断的风险。本文的主要贡献如下: 1)设计了一个边缘车辆网络中的动态卸载模型,为了在动态网络中成功卸载任务,定义了一个风险函数来评估任务卸载失败的可能性。 2)联合系统风险定义了一个新的卸载效用函数,并将此问题建模为任务卸载决策、功率分配和计算资源分配的联合优化问题,以最大化系统的总效用。 3)混合整数非线性规划问题是难以解决的,通过计算发现,可以将问题解耦成资源分配问题和具有特定解的卸载决策问题。进一步地,将资源分配问题分解为功率分配和计算资源分配,分别使用分式规划和凸优化技术进行求解。 4)仿真结果表明所提动态卸载方案能够得到近似最优解,这证明了该方案的有效性。3.2 问题分解
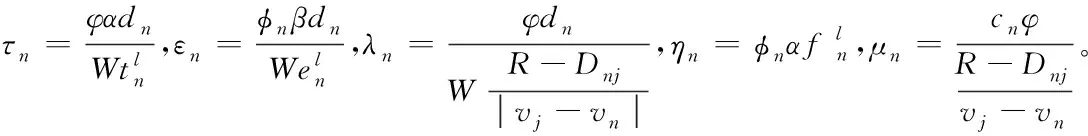

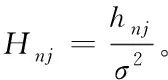
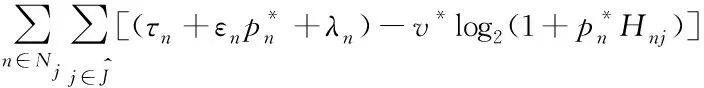



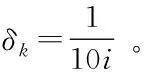

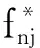

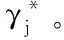

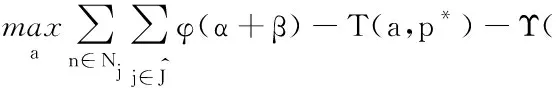

4 仿真分析



5 结论
