“二次函数图象与性质”教学设计与反思——核心素养视角下数学复习课的实践研究

林佳娜

(广东省广州市第九十七中学，510000)

笔者在广州市的教研活动中开了一节公开课,课题是“二次函数的图象与性质”,教学设计的核心环节是以下的开放性问题.下面对课堂的主要环节进行回顾与反思.

一、课堂核心部分回放

(一)开放性问题——基本图形我来读

二次函数y=ax2+bx+c的部分图象如图1所示,当x取一切实数时,请将图象补充完整,写出三个以上的正确结论并说明理由.

这是一个开放性问题，需要留给学生充分的思考时间.

设计意图通过相关结论的挖掘,旨在帮助学生对二次函数核心知识进行重点回顾．

(二)问题回想—数学味道我来品

1.方法解读—如何识图(脚手架)

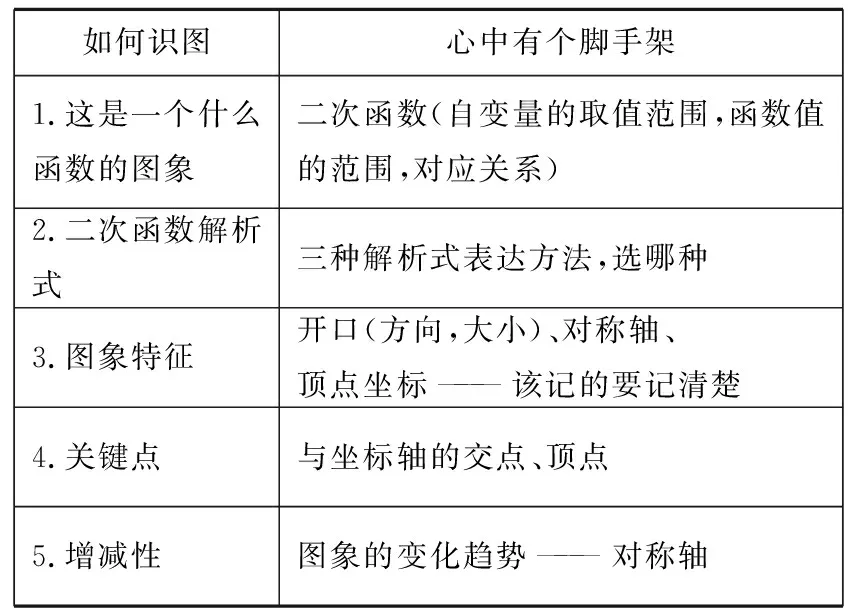
如何识图心中有个脚手架 1.这是一个什么函数的图象二次函数(自变量的取值范围,函数值的范围,对应关系) 2.二次函数解析式三种解析式表达方法,选哪种 3.图象特征开口(方向,大小)、对称轴、顶点坐标———该记的要记清楚 4.关键点与坐标轴的交点、顶点 5.增减性图象的变化趋势———对称轴

2.欣赏你的结论——由小见大,建构我的数学王国形(一个小小的图象)——数(一串长长的结论)表面的——深层的(多看多想).

(三) 问题延伸——题目我来编

在写结论过程中,你认为哪个条件最重要,想不想改变一下?编个题目来试试.

设计意图编题过程是课堂学习变式训练的延续.

二、复习课教学与反思

(一)备课反思—教学目标定位

首先,复习的目的是什么?其次,一节课时间就40分钟,能突破什么?这也是需要教师认真思考的.

本节课的教学目标:

1.复习二次函数图象与性质的基础知识(解析式、顶点坐标、对称轴、增减性).

2.让学生经历读图过程,学会多维度地识图读图,学习一般的提取图象信息的方法，学会对获得的信息进行归类,并纳入知识框架体系.

3.感受数形结合、转化思想在问题解决中的应用.

(二)目标达成的方法

1.找好问题

“自学·议论·引导”教学法告诉我们,好的“问题”要具有“数学味”;好的“问题”应尽量串联整节课.一个好问题,既能使课堂连接自然流畅，又能促进课堂的自然生成．实践证明,“好的问题”可以给学生节省很多宝贵的时间,还能避免学生掉进“题海”.

2.深入研究好问题

本节课有机会在课堂上生成下面这样的表格,教师一定要用好这样的资源.本节课教师呈现出研究函数的三个层面“形—数—结合点”流畅自然.

形数结合点图象与x轴有两个交点b2-4ac>0方程ax2+bx+c=0有两个不相等的实数根与x轴两个交点是(-1,0),(3,0);与y轴交点(0,3).方程-x2+2x+3=0有两个不相等的实数根,它们是x1=-1,x2=3,x1+x2=2,x1x2=-3y=0时,y=ax2+bx+c变成方程ax2+bx+c=0,x1+x2=-ba,而对称轴x=-b2a顶点坐标(1,4)方程ax2+bx+c=4有唯一解x=1,方程ax2+bx+c=5无解当m取何值,方程ax2+bx+c=m有解

仔细体会一下,这里

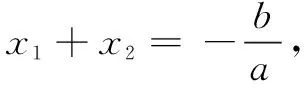
另一个过程:

x=1时,图象上对应点最高顶点坐标为(1,4),对称轴x=1⇒2a+b=0x=1时,a+b+c=4若x=m≠1,则a+b+c>am2+bm+c

对函数最高点的三个层次的理解,特别第三层，与方程自然联系渗透,难点消逝于无形.

3.课堂的主体是学生

要弄懂问题,学生可以依靠各种方法,如，自主发现、同伴交流、教师引导,最终都要落实到自己真正弄清楚、最好是能给同伴讲出来．笔者带的这个班，一直是在李庚南老师“自学·议论·引导”教学法指导下开展教学.学生很享受这种“有规则的自由”课堂.教师的课堂问题也基本是因学生而产生的.“一个问题,一串知识”或者“一串问题,一个知识”的问题模式,是课堂教学的常态,却让学生常常陶醉其中．

除了课堂上的学习,学生也有做数学笔记的习惯,还可能会整理学习的点点滴滴、及时地做错题分析和知识归纳.

4.课堂教学的引领者是老师

复习课最终是要教会学生思考:如何从表面的看到深层的(整体把握—局部突破—寻找联系).如何把杂乱变成有序(形—数—数形结合的结合点).

学生从零散地知道有这些知识,到有序地把它们纳入知识体系,再到建构自己的认知框架,都需要方法的引领.让他们平时养成了习惯,数学思维方法慢慢就自然形成．

(1)看整体

(2)读细节

抛物线与y轴的交点c在x轴上方c>0,c=3当x=0时,y=c.c决定图象与y轴交点的位置图象过点(-1,0)a-b+c=0(a+c=b)当x=-1时,y=a-b+c图象必过点(3,0)9a+3b+c=0当x=3时,y=9a+3b+cx=1时,图象对应点最高顶点坐标(1,4),2a+b=0.若m≠1,则a+b+c>am2+bm+cx=1时,a+b+c=4对称轴:x=-b2a=1顶点:-b2a,4ac-b24a 图象有在x轴上方的当-10任意举例子:如x=1时,y>0,即:a+b+c>0图象也有在x轴下方的当x<-1或x>3时,y<0x=4时,y<0,即:16a+4b+c<0等等图象有对称性y=3时,x=0或x=2(0,3)关于x=1的对称点(2,3)图象有增减性x<1时,y随x的增大而增大,x>1时,y随x的增大而减小图象的增减性由开口方向和对称轴共同决定

5.适时生成探索性问题

本节课的图象问题探索过后,有没有后续的探究问题？答案是肯定的,题目3个关键条件只要有一个变动,问题就动起来了.这种充满研究魅力的问题,师生当然不能错过.

引导学生思考:(1)对称轴变为x=n,其他条件不变,我们来研究研究.

从数的角度解释—用数式的方式,你怎么做?

y=a(x-n)2+k，过点(-1，0)，(0，3).

从a的表达式,你得到什么?何时开口向上?向下?

(2)若对称轴变为x=n,且n>0，其他条件不变,你能分析啊a+b+c的取值范围吗?

(三)课堂整体表现

在写结论环节,全班每一个学生的笔都动了起来.从独立探索结论,到后面的小组交流、归纳汇总、教师在整堂课上并没有叫学生解哪一道具体的题目.但一节课下来,学生经历了图象提取信息、解读信息、分类汇总的过程,他们已经做了不少题.学生身心愉悦,以非常积极的状态投入到了学习中来,这是教师所乐于见到的.这也从另一个角度告诉我们,学生是充满学习智慧的,等待良师用心去栽培.