基于田口法的潜油电机槽型优化研究

金 颢 ，张俊斌，高晓飞，潘雅缤2，单彦魁，刘 佳

(1. 中国海洋石油有限公司 深圳分公司，广东 深圳 518067；2.大庆油田力神泵业有限公司，黑龙江 大庆 163311)

目前，我国主要大型油田都已经建立了几十年，开采出的原油中水分、杂质含量也在逐年增高[1]。虽然近些年来全国各地发现了储备巨大的页岩油，但其开采难度大、效率低，仍然是待攻破的重要难题。近些年来，以潜油电机为核心部件的潜油电泵系统凭借结构简单、举升效率高、耐高温高压高腐蚀等特点，已经逐渐取代传统游梁式开采设备。目前的潜油电泵机组主要由潜油电机、保护器、分离器、离心泵4部分组成，其中潜油电机作为整个潜油电泵机组的核心动力元件，其性能指标直接决定了整套机组的工作性能[2]。在满足油井要求的前提下，提高潜油电机主要性能指标，可有效降低采油成本，提高工作效率。

为提高潜油电泵机组的工作性能，对潜油电机进行优化设计是必然趋势。20个世纪60年代，电机优化设计就已经被提出，最开始只是通过简单的推演寻求一种最优方案的途径。随着计算机技术和现代智能算法的发展，近些年提出来多种智能优化算法，例如蚁群算法、遗传算法、混沌算法、神经网络等等；21世纪开始，国内外开始利用免疫遗传算法和蚁群算法对潜油电机进行优化设计[3-4]，通过设置优化变量、约束条件、建立优化数学模型，实现优化目标。以上优化算法主要采用全局优化方法，计算复杂，优化过程较长，在实际应用中并不方便。

本文提出一种基于田口法的新型优化方案。田口法可以通过局部约束，同时对多个参数进行优化设计，通过正交仿真分析，减少试验次数，快速找到最优组合[5]。目前，田口法主要用于永磁同步电机优化设计中，通过仿真试验，在保证相应参数的基础上，获得了较为理想的结果。由于潜油电机细长的结构，定转子通过隔磁段和扶正轴承相连接，其优化设计过程很难通过传统电机设计程序完成[6-8]；尤其对定转子尺寸这种无法简单运算出目标函数关系的参数，运用田口法可有效解决这一问题[9-11]。

1 潜油电机有限元模型

潜油电机是一种立式三相异步电动机，由于其特殊的工作环境，一般都做成细长的结构，通常由多节组成，节与节之间通过扶正轴承和隔磁段相连接[12]。潜油电机内部采用密封结构，通过充满电机油形成闭合油路，起到润滑、绝缘、传热的作用。潜油电机结构如图1所示。

1—止推轴承；2—电机头；3—壳体；4—扶正轴承；5—下接头。图1 潜油电机结构示意

1.1 槽型结构设计

潜油电机安装在油井底部， 需要匹配油井尺寸进行设计，普遍做成细长结构。定转子外径尺寸与轴向长度比很小，导致潜油电机槽型结构选择性较少，一般定子可选用闭口或半闭口的梯形、梨形、方形槽设计，转子可采用闭口或半闭口的圆形、梨形、梯形槽设计。

1.2 有限元模型分析

根据潜油电机结构数据，利用有限元法建立二维有限元仿真模型，分析电机内部电磁场分布规律，联合电磁设计过程，通过场路结合手段，得出潜油电机设计方案。有限元模型如图2～3所示。

图2 潜油电机有限元模型

图3 潜油电机剖分图

2 槽型优化研究

2.1 潜油电机田口法模型

田口法是一种低成本、高效益的质量工程方法，强调产品质量的提高不是通过检验，而是通过设计。潜油电机槽型结构对性能具有重要影响，且影响关系复杂，很难通过传统电磁计算手段得出准确结论。借助于田口法的基本思想，把性能的稳健性设计到电机制造过程中，通过控制源头数据来抵御大量的噪声或不可控因素的干扰，进而提升潜油电机性能，减少优化时间，加快优化进程[13-15]。潜油电机田口法模型流程如图4所示。

图4 潜油电机田口法模型流程图

2.1.1 潜油电机槽型优化因子

潜油电机由于其特有的细长结构，定转子外径尺寸受井口参数约束，无法进行大规模调整，定转子槽极配合比较固定。例如143系列潜油电机普遍采用两极、定转子18/23的槽配合方案，定转子槽型结构如图5所示。

图5 潜油电机槽型结构

基于潜油电机定转子外形尺寸、温升条件、机械强度不变的情况下，对槽型优化因子进行选择，分别选取定子斜肩角α1、定子槽高h12、定子槽宽b1、转子斜肩角α1、转子槽高hr12和转子槽宽br1为优化因子[16-18]。此时，为满足定转子导体有效横截面积及定转子槽口尺寸不变的情况下，在调整以上6个优化因子的同时，还需要对定子槽底宽b2、转子槽底宽br2进行调整，但不计入优化因子。对优化因子分别选取5个不同的水平取值，建立优化因子与水平正交表，如表1所示。

表1 潜油电机优化因子与水平正交表

正交表是运用组合数学理论在正交的基础上构造的一种规范化表格，记为Ln(ji)。 其中：L为正交表的符号；n为正交表的行数(试验次数)；j为正交表中的数码(因素的位级数)；i为正交表的列数(实验因素的个数)。

2.1.2 优化目标

考虑潜油电机需要常年持续工作，故效率决定了油井的开采率，同时油井分布广泛，数目较大，每台电机的功率因数直接决定了供电系统中有功与无功的比例，所以把功率因数确定为优化目标[19-20]；最后考虑工作过程中的扰动和启动问题，将最大转矩倍数与启动转矩倍数也作为优化目标。最终确定电机效率η、功率因数cosφ、最大转矩倍数Tmax及启动转矩倍数Tst为本模型的优化目标。

2.1.3 模型仿真计算

本研究建立6个优化因子、水平数为5、4个优化目标的田口法模型，对不同组合方案进行有限元仿真，寻求各优化因子对优化目标的影响程度。该方法通过建立正交模型L25(56)，可有效降低仿真次数，节约计算时间95%以上。正交矩阵为：

具体仿真试验结果如表2所示。

表2 正交矩阵模型仿真结果

2.2 优化分析

基于正交模型仿真结果，可分别获得不同电机性能优化目标的平均值，如表3所示。

表3 各优化目标平均值

利用平均值法，求解不同优化因子对各优化目标的目标值，如表4所示。

表4 优化目标值

由表4可以看出：

1) 效率与定子槽高、定子槽宽呈负相关关系，与转子斜肩角、转子槽高、转子槽宽呈正相关关系，与定子斜肩角呈先增加后减小，且在水平4时为最大值。

2) 功率因数与定子斜肩角呈正相关关系，与定子槽宽、转子槽高、转子槽宽呈负相关关系，与定子槽高呈先增加后减小，且水平2时为最大值，与转子斜肩角基本维持不变。

3) 最大转矩与定子、转子斜肩角呈先增加后减小，与定子槽高呈负相关关系，与定子槽宽、转子槽高、转子槽宽呈正相关关系。

4) 启动转矩与定子槽高、转子斜肩角、转子槽高呈负相关关系，与定子槽宽、转子槽宽呈正相关关系。

由此可以分析出不同优化因子对优化目标的单独影响，但电机优化设计需要综合考虑所有优化目标，确定一个最优方案。本研究借助统计学方法，得出不同优化因子对各优化目标的影响程度，如表5。

表5 潜油电机各优化因子影响程度

由表5可以分析出，定转子斜肩角对各优化目标影响程度较小；定转子槽高对电机效率影响较大；功率因数主要受定子槽高与槽宽影响；定子槽宽主要决定了最大转矩与启动转矩倍数。

2.3 对比分析

根据以上分析，结合各优化因子对优化目标的影响程度，在满足功率因数的前提下，确定潜油电机定转子槽型结构优化方案。以143系列210 kW潜油电机为例，其优化前后性能对比如表6所示。

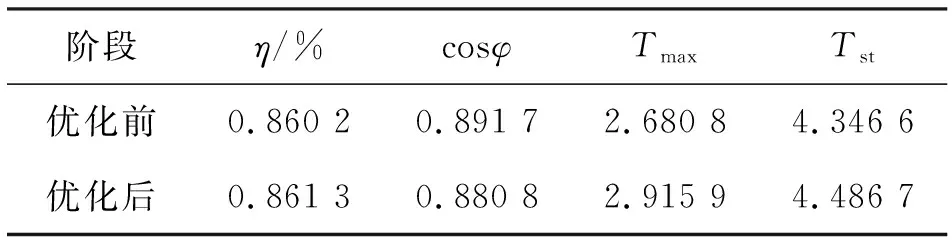
表6 优化前后性能对比

结果表明，通过田口法对潜油电机定转子槽型进行优化后，在保证功率因数满足条件的基础上，其效率、最大转矩、起动转矩得到了不同程度的提升，其中效率提升效果最为明显。优化后的潜油电机有限元瞬态场仿真结果如图6～7所示。

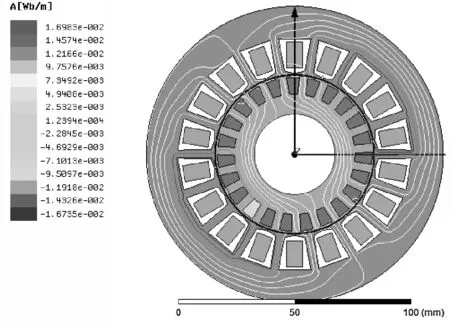
图6 潜油电机磁力线分布

图7 潜油电机磁通密度云分布

3 结语

潜油电机定转子槽型尺寸对其性能指标具有一定影响，但很难直接用数学函数确定影响关系。传统的电磁设计过程繁琐，无法进行大量优化设计。本文以场路结合的手段，并以田口法为基础，通过确定槽型优化因子与优化目标，建立潜油电机槽型优化目标正交矩阵。通过统计学方法确定各个优化因子对优化目标的影响关系和影响程度，确定最终优化方案。以1台143系列210 kW的潜油电机为例，验证该方法的可行性，为后续研究潜油电机优化设计起到辅助作用。