基于燃料电池的复合电源式装载机分层控制

张志文,杜文杰,梁君飞,张艳岗,武雅文

(1.中北大学 能源与动力工程学院,太原 030051; 2.燕山大学 车辆与能源学院,秦皇岛 066004)

当今社会通过科技变革与新能源技术创新推动着汽车的节能减排[1]。在工程机械领域,传统的工程机械排放大,能量利用率低,造成能源浪费与环境污染等问题[2-3]。近年来,国内外通过混合动力、纯电动驱动等技术来提高工程机械能源利用率,国外工程机械生产厂商如卡特彼勒、沃尔沃、约翰迪尔、日立建机、川崎等新能源工程机械产品早已商业化[1]。

文献[4]以某5t轮式装载机为研究对象,探索工程机械新能源汽车新技术。装载机需求功率变化频繁、整车冲击振动剧烈,因此,新能源装载机能量部件需要具备高功率密度与高能量密度的特性,储能元件应具有快速充放电特性与高循环寿命。

本文设计燃料电池复合电源式装载机。以燃料电池作为主动力源、超级电容作为辅助能源构建复合电源系统,通过电力驱动满足负载液压系统与行走系统的需求。在不同负载工况下,控制系统通过调节功率分配因子动态调节燃料电池与超级电容功率输出以满足装载机工况需求。要发挥复合电源的优势需充分利用超级电容功率密度高、循环寿命长、充放电速度快的优点及燃料电池高效率、零排放、寿命长、能量密度高的优点。

韩国于2016年着手燃料电池挖掘机的商用化,2018年氢能经济路线图提出要“培育以燃料电池叉车和挖掘机为中心的氢能建筑机械产业”。2020年3月,现代工程机械、现代摩比斯与现代汽车联合开发全球首台氢动力工程机械设备,计划于2023年进行批量生产和分销。2020年7月,英国工程机械生产商JCB开发出建筑行业第一台氢动力挖掘机,已在试验场对一台由氢燃料电池驱动的20t220X挖掘机进行了为期12个月的测试。2020年3月,潍柴动力股份有限公司氢燃料电池发动机工厂正式投产使用,预计年产量约20000台,这是其氢燃料电池商业化的关键一步。

高效合理的能量管理策略是解决复合电源系统功率分配的关键。2017年,法国贝松实验室Munoz等[5]提出了基于电池和超级电容总功率共享的实时控制策略,建立非线性自回归神经网络预测模型,设计了离散小波变换的时域滤波器,延长了动力电池的寿命,控制策略具有良好的鲁棒性。2018年,Ben Elghali等[6]研究了以质子交换膜燃料电池为主体的应用于汽车上的复合电源系统,提出了一种基于自适应滤波的能量管理策略,采用模糊逻辑动态调整分离频率,驱动循环仿真表明,燃料电池与超级电容都取得了良好的性能。S.G.R.E机构的Ibrahim等[7]基于模糊逻辑、向量机控制、频率解耦等策略研究燃料电池汽车能量管理,改善了电动汽车动态响应速度和稳定性,根据动力电池充放电状态、燃料电池氢气消耗量、整车效率等参数进行参数匹配。浙江大学Zhang等[8]在2019年通过多层感知与神经网络方法提取复合电源系统的特征参数,通过驱动模式识别实现燃料电池和超级电容实时功率优化分配。

文献对燃料电池复合电源系统的研究集中在汽车上,在工程机械领域的研究甚少,由于工况的差异性导致工程机械复合电源系统控制策略更加复杂。为了满足装载机工况需求,动力系统需实现大功率和高能量的双重目标,本文将燃料电池和超级电容组成复合电源系统,在频繁变化的工况下,由于超级电容的存在,可以瞬间动态平衡负载功率需求,同时燃料电池能够提供稳定的功率输出。因此,超级电容与燃料电池组成的复合电源系统是解决电动装载机电源问题的重要途径[9],但复合储能使得系统的功率与能量流变得更加错综复杂,目前亟须新技术解决多模式能量分流关系,制定高效合理的能量管理与优化策略,才能充分发挥复合储能系统的性能和优势,也是打破工程机械车载储能技术瓶颈的关键。

本文通过分析传统装载机工况特征,采集各动力系统的性能参数,设计复合电源式装载机动力传动方案,对燃料电池、超级电容、动力驱动等系统进行建模;考虑到系统能量管理过程中一些混沌和暂态需求功率分量对复合电源系统耦合特性和燃料电池耐久性的影响,基于三阶Haar小波变换分解需求功率;设计模糊逻辑控制策略,将小波处理后的低频负载分量、超级电容SOC值作为输入,输出功率分配因子,以系统的经济性为控制目标对复合电源系统进行功率分配;基于粒子群(particle swarm optimization,PSO)算法优化模糊逻辑隶属度函数,提高复合电源系统的效率与寿命,并提高动力系统的响应速度。

1 系统传动方案及模型建立

如图1所示,燃料电池和超级电容组成复合电源系统作为纯电动轮式装载机的能量系统,通过电动机为动力传动系统与液压系统提供动力,控制器根据实时采集工况数据进行能量管理。

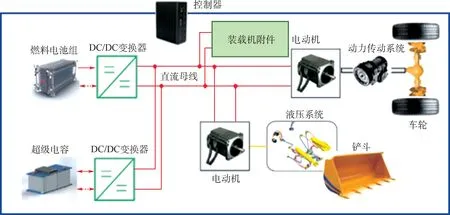
图1 复合电源装载机动力传动方案Fig.1 Power transmission scheme of hybrid power loader

复合电源系统主要包括燃料电池、超级电容、DC/DC变换器等元件,通过电力驱动将动力分配到工作液压系统和行走系统[4]。超级电容作为辅助电源配合燃料电池系统完成装载机各个工况需求,在装载机起步、重载、能量回收、负载变化剧烈等工况时,通过超级电容的“削峰填谷”保证电动装载机系统的高效稳定工作,并延长燃料电池系统的寿命。因此,针对不同工况需求,需要探索耦合系统的能量管理方案,首先对装载机系统进行模型建立。

1.1 燃料电池模型

燃料电池标准理论可逆电动势Eref为

式中:ΔG为燃料电池系统的吉布斯自由能;n为氢气的电子数;F为法拉第常数。

燃料电池输出电压EFC为

式中:Eact为活化过电势;Eohm为欧姆过电势;Econ为浓差过电势。

燃料电池电压与电流密度变化有关,电流密度较低时,由活化极化和欧姆电压损耗引起的电压损失起主要作用,而在高电流密度时,由浓度极化引起的电压损失占主导作用[10]。图2为燃料电池的极化曲线,曲线分别代表阴(RHca)、阳(RHan)两极不同相对湿度下的曲线。

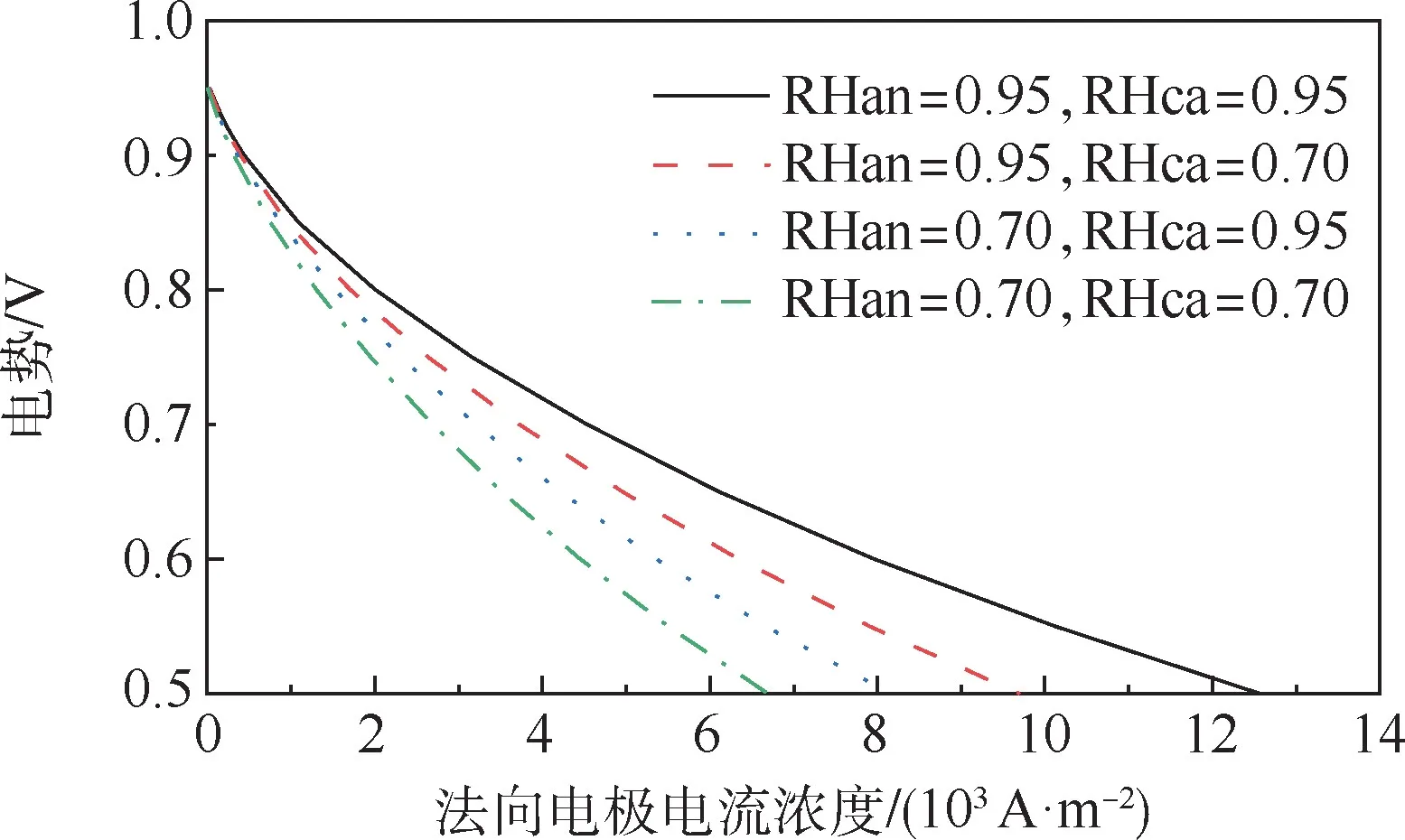
图2 燃料电池极化曲线Fig.2 Polarization curves of fuel cell

通过MATLAB/Simulink平台建立燃料电池系统模型Simulink模型,其结构如图3所示。

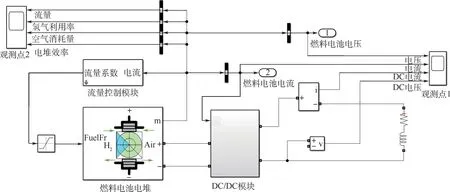
图3 燃料电池模型结构Fig.3 Structure of fuel cell model

1.2 超级电容模型

电容的容量取决于两极板间存储的电荷量。图4为超级电容等效电路模型,主要由并联电容器C、串联充放电电阻R1、并联自放电损耗电阻R2组成[10]。

图4 超级电容等效电路模型Fig.4 Equivalent circuit model of super capacitor

超级电容输出端电压U0、等效电容电压U与放电电流I的关系为

超级电容的荷电状态(SOC)取决于输出端电压,其值为

式中:Urt为超级电容实时电压;Umax和Umin分别为超级电容最大和最小工作电压。

根据以上超级电容等效电路数学公式建立如图5所示的MATLAB/Simulink模型。

图5 超级电容模型结构Fig.5 Structure of super capacitor model

1.3 其他模型

1)整车动力传动模型

装载机动力平衡方程表示为[10]

式中:Ft为驱动力;Ff为滚动阻力;Fw为空气阻力;Fi为坡度阻力;Fj为惯性阻力。

2)电动机模型

建立永磁同步电机力矩平衡方程[10]:

式中:Tm为电动机的电磁转矩;TL为电动机负载转矩;J为电动机的转子及负载惯量;ωm为电动机角速度;B为黏滞摩擦系数。

基于以上数学模型在MATLAB/Simulink平台建立如图6所示电动机模型。

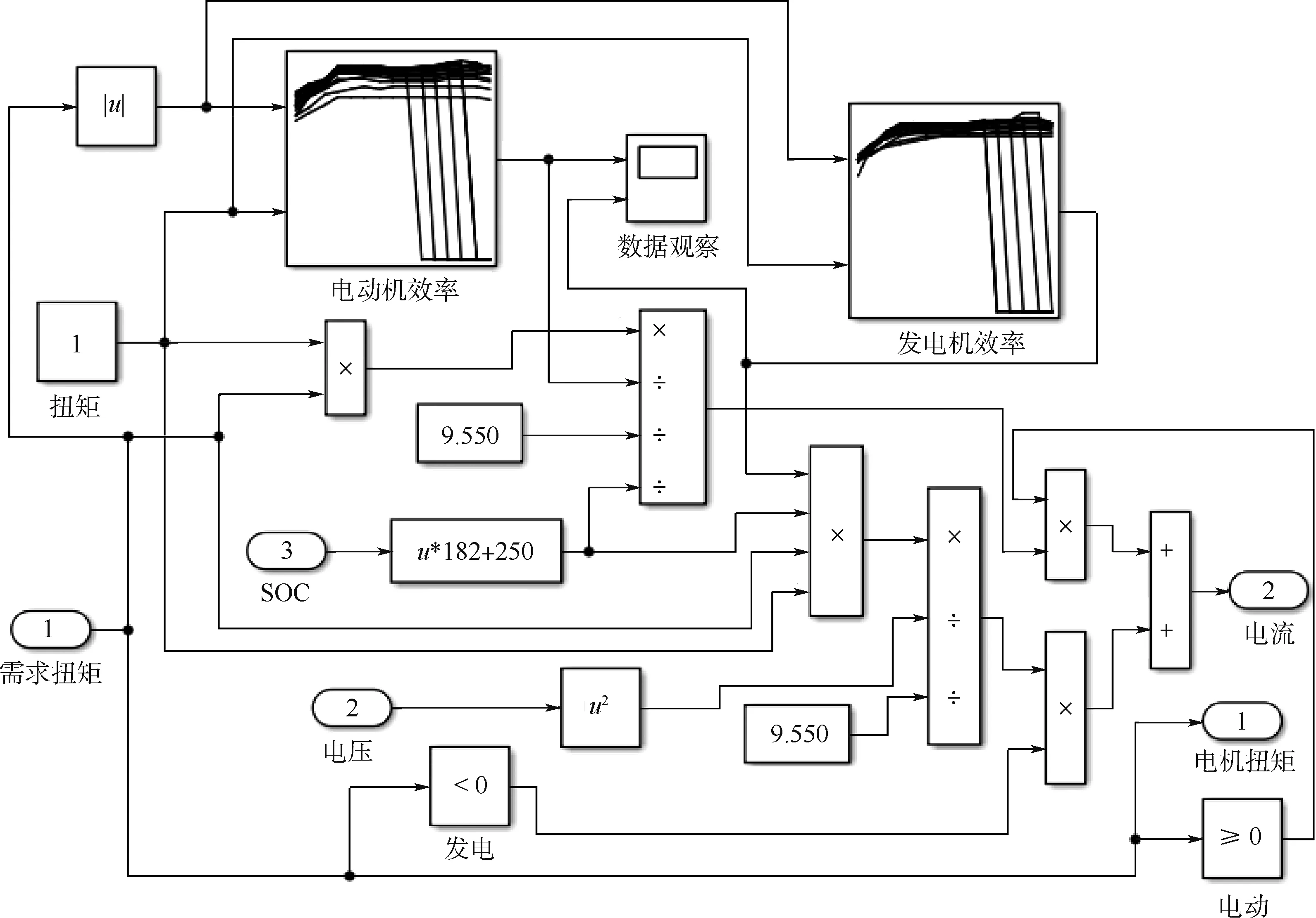
图6 65kW/125kW电动机模型结构Fig.6 Structure of65kW/125kW motor model

3)液压系统模型

液压泵出口压力转换成泵驱动转矩,液压系统总消耗转矩TP为[10]

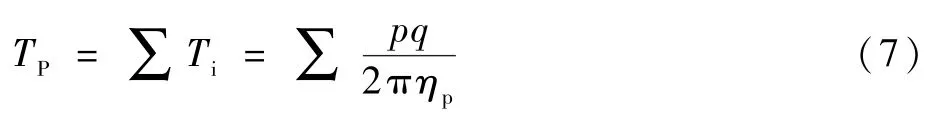
式中:Ti为各液压泵驱动转矩;p为各液压泵的出口压力;q为各液压泵排量;ηp为各液压泵机械效率。

2 燃料电池复合电源能量控制策略

2.1 装载机工况特性分析

图7为装载机作业循环过程,其工况特点是:作业循环周期短,整车频繁起停,功率变化频率与幅度大,驾驶员需要频繁加减油门、变换挡位、操控转向与工作液压系统。因此,对于燃料电池复合电源装载机循环工作过程中,输出功率、车速、载荷等相关参数频繁变化,控制系统需根据装载机的负载工况特性进行分析,并制定对应的控制策略。

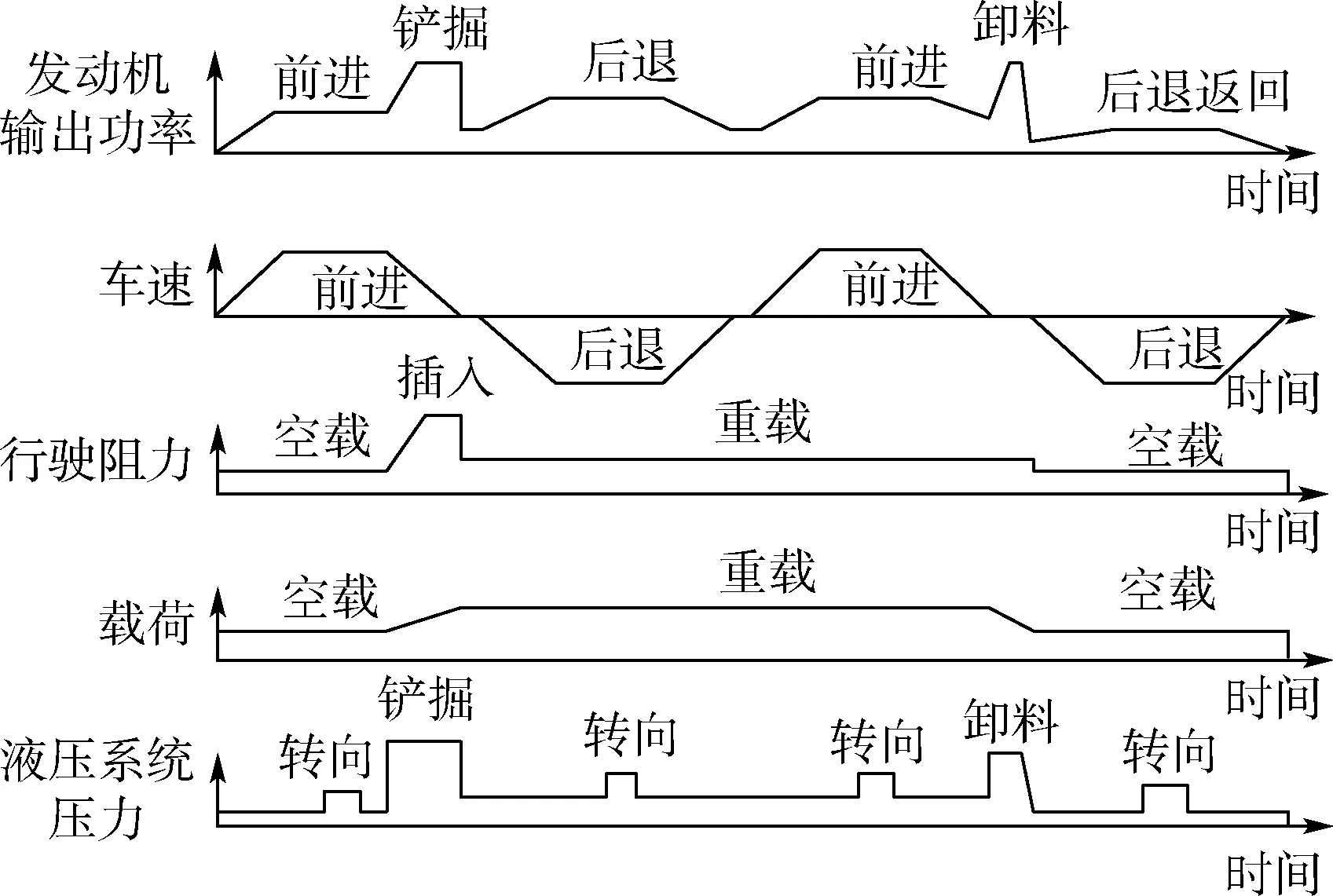
图7 装载机工作示意图Fig.7 Working diagram of loader

2.2 燃料电池复合电源系统控制策略

为了满足复合电源式装载机对功率和能量的双重需求,控制系统需要将燃料电池和超级电容输出功率进行实时分配。但复合储能使得动力系统的功率与能量流变得更加错综复杂,需制定高效合理的能量管理与优化策略,解决多模式能量分流关系,才能发挥复合电源系统的性能和优势。

图8为控制系统工作结构。装载机复合电源能量控制系统主要工作过程如下:首先,根据复杂工况下系统多状态模型,通过模型仿真探索复杂工况对系统耦合特性。然后,基于Haar小波理论进行功率分配,用超级电容平衡需求功率中混沌和暂态分量,将低频分量输入到模糊逻辑控制器中进行功率分配。最后,通过PSO算法优化模糊逻辑隶属度函数,优化功率分配因子,实现多能源系统的最优能量控制策略。

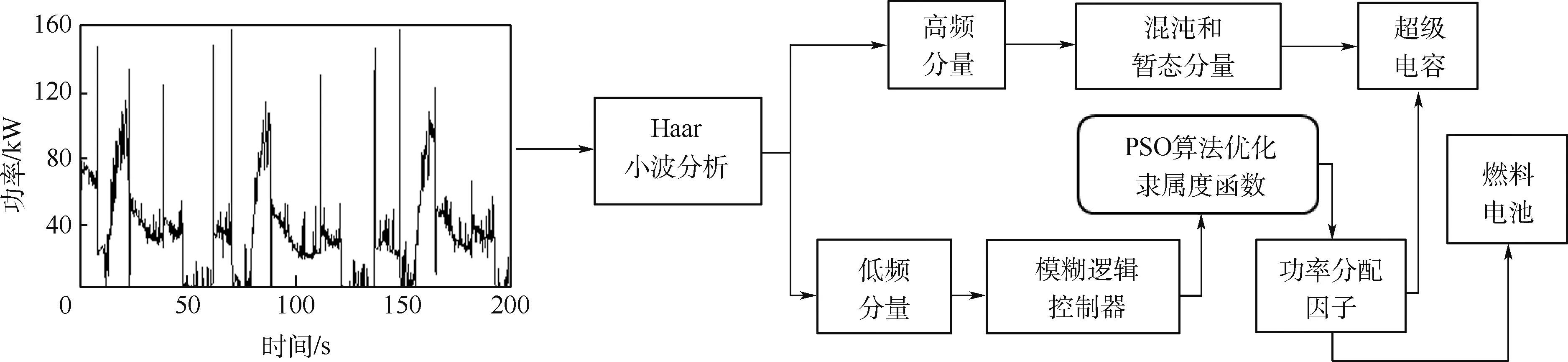
图8 整车控制系统结构框图Fig.8 Structure block diagram of vehicle control system

装载机在复杂工况下,通过调节功率分配因子对燃料电池和超级电容进行功率分配与分层优化控制,分析多系统耦合特征,探索分层优化控制的机理,以满足装载机的工作需求,提高装载机能源利用率。挖掘复合电源的性能潜力,实现系统综合性能最优。

2.3 小波功率分配

小波理论用于将给定的函数或连续时间信号分成不同尺度的分量,该技术已经成功应用于多数字信号处理和压缩领域。装载机工作过程中频繁处于功率波动、启停变化、怠速和大功率运行状态。剧烈的功率波动和频繁的启停变化是燃料电池性能衰退的关键影响因素[11-12]。因此,在复合电源系统中将需求功率进行小波分配,避免燃料电池应对一些混沌和暂态功率分量,提高燃料电池的耐久性和复合电源系统的可靠性。

Haar小波与其他小波相比在时域上具有最短的滤波长度,非常适合装载机负载功率频繁变化的特点。本文使用Haar小波变换策略提取系统需求功率暂态信号。Haar函数ψ(x)为

式中:x为时间。

本文将装载机实际载荷谱曲线加载到Haar小波变换策略中,将负载功率曲线分解为高频和低频部分,燃料电池系统主要负责低频功率部分,高频分量及制动能量回收部分由超级电容负责。考虑计算效率和频率的限制,设置3层小波分解,解压缩和重构滤波器分别为[H1(z),H0(z)]T和[G1(z),G0(z)]T。输入信号x(t)采用3级Haar小波分解和重构。如图9所示,分解和重构的过程分别采用下采样和上采样的方法,H0(z)与G1(z)为低通滤波器,H1(z)与G0(z)为高通滤波器。原始信号x(n)等于装载机负载功率谱的预定功率需求。

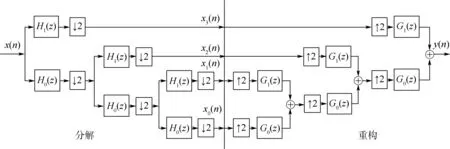
图9 Haar小波信号处理Fig.9 Haar wavelet signal processing

将装载机实车功率载荷谱作为原始信号x(n)。经过3层Haar小波变换处理,原始信号被划分为x0(n)、x1(n)、x2(n)、x3(n)来描述频率的特征。低频分量PLC和高频分量PHC分配表达式为

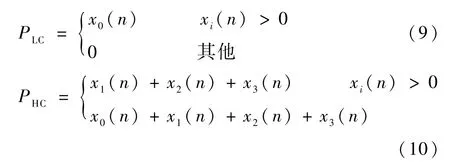
低频分量为需求功率中稳态分量,将其作为模糊逻辑控制器的输入变量,而高频分量是需求功率中混沌和暂态分量,由超级电容平衡。

2.4 模糊逻辑控制策略

本文的控制策略目标是:通过调节功率分配因子满足装载机工况需求,使复合电源与负载更好地匹配,系统各元件高效工作,提高整机效率和燃料电池系统的寿命。复合电源装载机控制系统的特点是:动力驱动系统输出功率非线性突出,工作环境的复杂多变导致控制参数突变与信号失真,负载载荷具有很强的鲁棒性,控制单元复杂繁琐,因此很难建立精确的数学模型。模糊逻辑控制策略把人的经验控制用计算机实现,基于人的控制经验建立控制系统的知识模型,定义模糊语言变量,确定模糊集合,设计模糊逻辑推理程序,实现高鲁棒性自适应的非线性控制[13-14]。本文基于模糊逻辑理论研究复合电源装载机系统控制策略,通过实时采集负载载荷数据与超级电容SOC值,控制燃料电池与超级电容系统工作点。

根据装载机工况特征对其负载特性及能量流向进行分析,实现工况划分并制定相应的工作模式[5]。根据装载机、燃料电池和超级电容的特征及工况需求,划分4种工作模式来适配混合动力能量源[15]。控制器工作模式分为以下4种模式[10]。

1)模式1。起步,超级电容独立驱动车辆。

式中:Pdem为装载机需求功率;PFC为燃料电池系统的输出功率;Pm为电动机的输出功率;PSC为超级电容输出功率;ηm为电动机输出效率。

2)模式2。燃料电池系统独立驱动车辆,燃料电池系统在自己约束条件内满足需求功率并同时平衡超级电容SOC值。

式中:SOC、SOCe、SOCh、SOCl分别为超级电容的荷电状态、荷电状态期望值、设置的超级电容荷电状态的最大、最小值;PC为超级电容SOC的调节功率;ηDC为燃料电池DC/DC变换器效率。

3)模式3。超级电容和燃料电池联合驱动,若超级电容的SOC值大于期望值,超级电容参与工作并提供较大功率,剩余需求功率由燃料电池系统提供。若需求功率较大,单纯燃料电池无法满足要求,需要超级电容放电以平衡负载需求。

式中:PFC-max为燃料电池最大输出功率。

4)模式4。制动回收模式,在车辆减速刹车或降臂时,电动机以发电模式工作,超级电容吸收能量而燃料电池系统不工作。

复合电源系统模糊逻辑控制结构如图10所示,采用功率控制,控制器的输入变量是系统需求功率Pdem与超级电容SOC值,输出为功率分配因子K。需求功率为工作液压系统和行走系统驱动功率之和,SOC值为超级电容的荷电状态[10]。

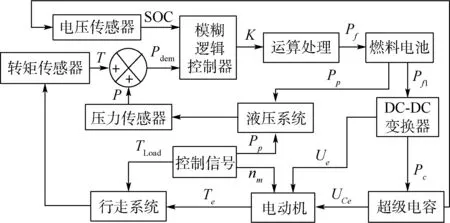
图10 复合电源系统模糊逻辑控制结构Fig.10 Fuzzy logic control structure of composite power supply system

在模糊逻辑控制系统中,首先设定输入与输出参数的基本论域,然后设计模糊逻辑控制器并制定控制规则,模糊逻辑控制器如图11所示。

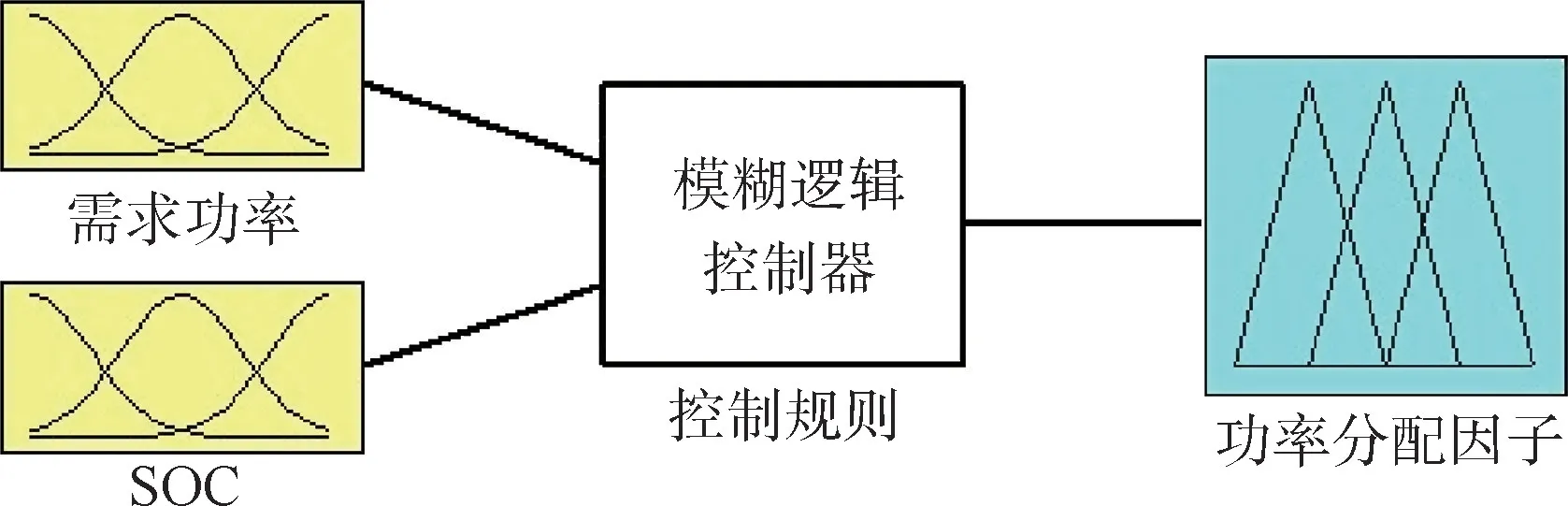
图11 模糊逻辑控制器Fig.11 Fuzzy logic controller

在该模糊逻辑控制器中,输入变量1为小波处理后整车需求功率Pdem,设置模糊论域为[0,160],Pdem的模糊子集划分为{VL,L,A,H,VH};输入变量2为超级电容SOC值,设置模糊论域为[0,1],超级电容SOC的模糊子集划分为{vlow,low,mid,high,vhigh};输出变量燃料电池系统功率PFC设置模糊论域为[10,100],燃料电池PFC模糊子集为{L1,L2,L3,L4,L5}。根据不同工况制定模糊规则集,建立隶属度函数,根据专家库制定控制规则,图12为对应的调节规则。

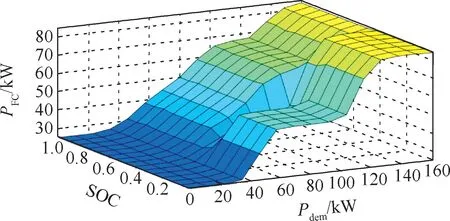
图12 Pdem、SOC、PFC对应的调节规则Fig.12 Regulation rules of Pdem,SOC and PFC

2.5 小波变换-模糊逻辑控制器

基于小波变换算法分离高低频需求功率,基于MATLAB代码来确定最优的3层分解阈值[16],对应d1、d2、d3最优值为10.6645、14.4748、6.8130;3层Haar小波处理后对应的负载功率曲线如图13所示,s/ds=a3+d3+d2+d1,其曲线为原功率,a3代表的曲线为分解后的低频功率曲线,d1、d2、d3代表超级电容负责的高频功率部分[10]。

图13 三层Haar小波处理载荷谱曲线Fig.13 Three-layer wavelet processing of load spectrum curves

经过最优阈值3层Haar小波处理后,将需求功率进行分配,一些混沌和暂态分量用超级电容平衡,有效提升燃料电池系统的寿命与整车经济性。图14和图15为3层Haar小波处理后的装载机典型工况下功率分流结构。该工况是以某5t轮式装载机(ZL50)为例,分析其对原生土进行作业时的载荷谱数据,控制器通过各传感器实时采集车速、动力传动轴转矩、工作液压泵出口压力及流量、转向液压泵出口压力及流量等数据。由图14和图15可见,分解后的燃料电池功率需求曲线具有全局低频性,将低频分量输入到模糊逻辑控制器中。

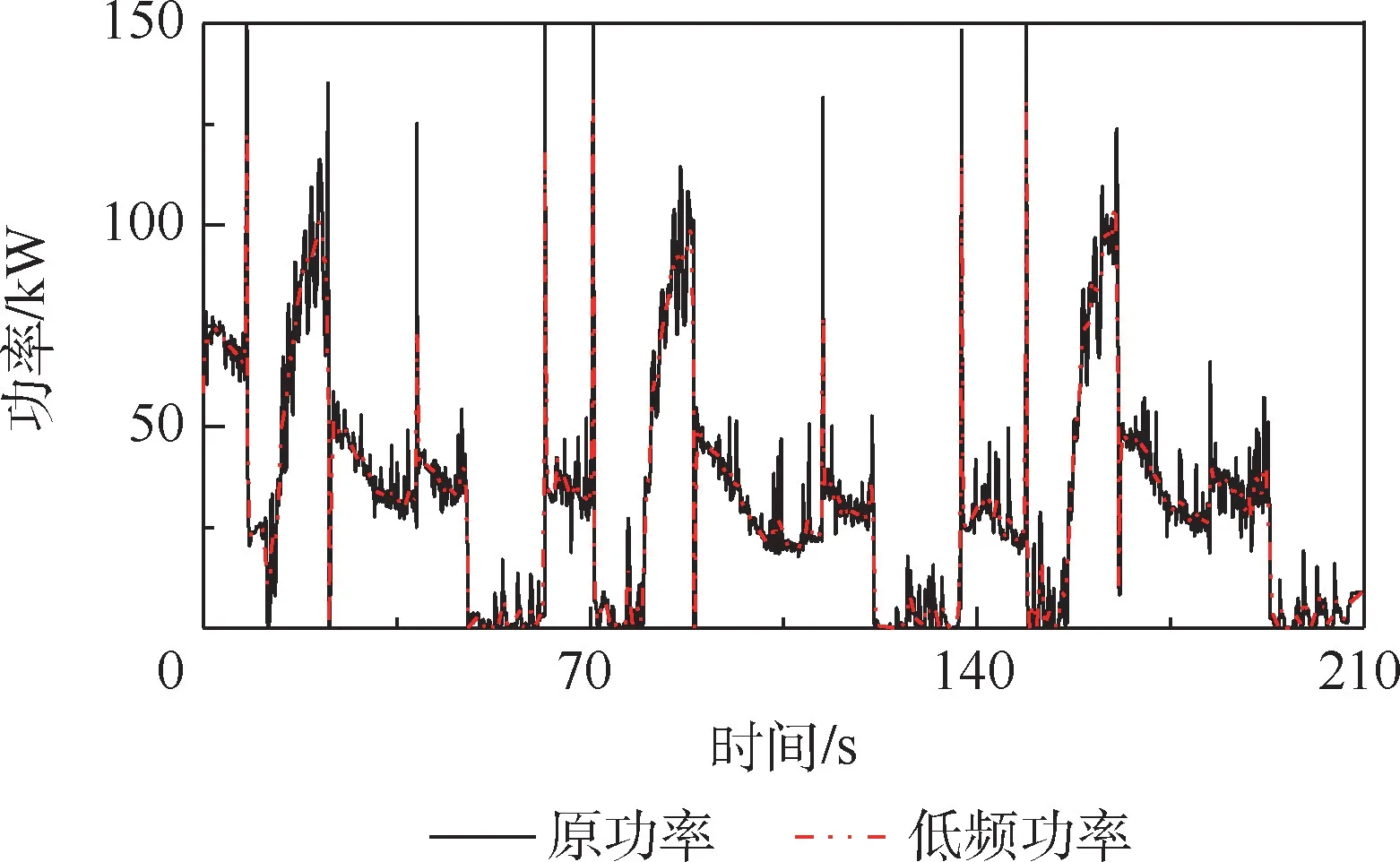
图14 动力系统负载功率曲线Fig.14 Load power curves of power system

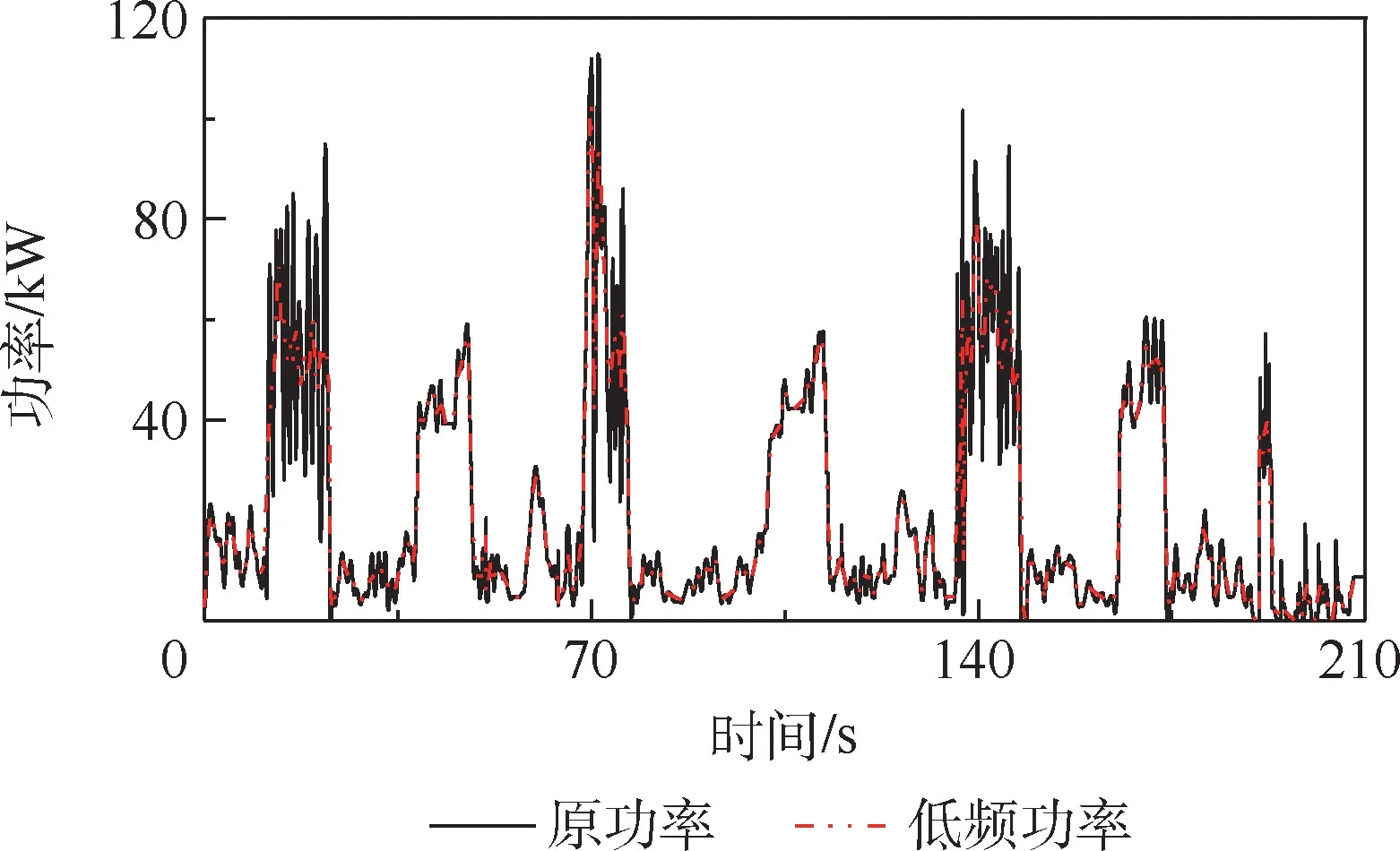
图15 液压系统负载功率曲线Fig.15 Load power curves of hydraulic system

将实际载荷谱数据低频分量加载到Simulink模型中,模型主要包括燃料电池系统、超级电容系统、发电机、电动机、工作液压系统、控制模块等。建立复合电源装载机系统仿真模型,研究系统动力耦合特性,将复合电源控制策略集成到整车控制层中,挖掘复合电源的性能潜力。其仿真模型如图16所示。

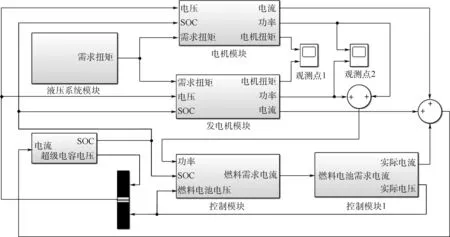
图16 复合电源系统仿真模型Fig.16 Simulation model of composite power supply system

将载荷谱功率数据作为模型输入,通过一个周期的对比仿真分析。图17为超级电容SOC值变化曲线,图18为燃料电池输出功率。对比可知,载荷功率经过3层Haar小波变换后,超级电容SOC值变化更加频繁,燃料电池功率变化幅度减缓,兼顾经济性的同时提高燃料电池寿命。因为超级电容在控制过程中平衡负载功率的暂态与混沌分量,导致SOC值变化幅度相对剧烈,但在0.6左右处于动态平衡状态,Haar小波变换后燃料电池输出功率更加平滑,图中局部放大处波峰功率下降了4.14kW,因此,小波变换提高了系统综合效率,控制策略更合理。

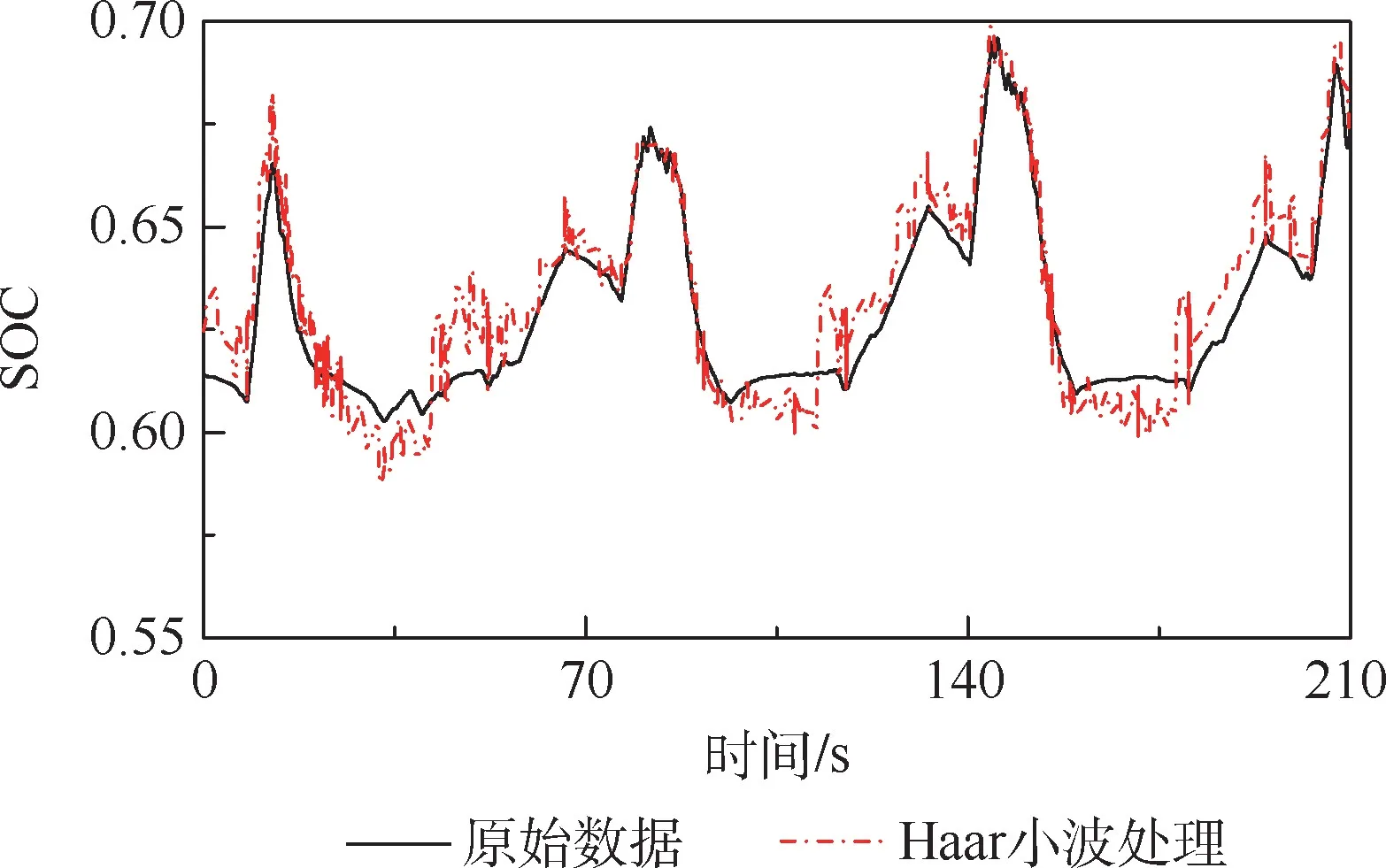
图17 超级电容SOC变化曲线Fig.17 SOC curves of super capacitor

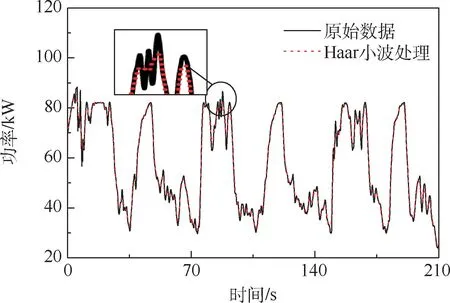
图18 燃料电池输出功率曲线Fig.18 Output power curves of fuel cell

3 PSO算法优化模糊逻辑隶属度函数

由于模糊逻辑推理过程依靠丰富的专家经验,需要反复训练才得到最佳控制模式,PSO算法采用简单速度-位置更新公式迭代,粒子通过交换自己的成功经验信息来寻求最优解[17-18]。为适合复合电源装载机系统工况特性,利用PSO算法优化模糊逻辑隶属度函数,实现复杂工况下系统功率分配及优化控制策略,提高系统综合性能。

3.1 PSO算法原理

首先,在一个设定的D维空间中进行目标搜索,搜索粒子群落由N个粒子构成,其中第i个粒子表示为D维空间的向量。第i个粒子的“飞行”速度也是一个D维向量,第i个粒子迄今为止搜索到的最优位置称为个体极值,最优位置是由整个粒子群到此为止搜索到的,记为全局极值,找到全局最优位置和个体极值最优位置时,粒子在这时会根据如下公式更新速度和位置[19]。PSO算法的具体流程如图19所示。

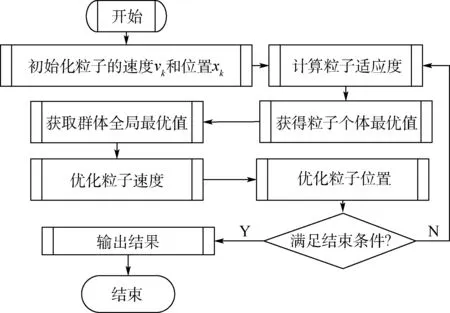
图19 PSO算法优化流程Fig.19 Flow chart of particle swarm optimization algorithm

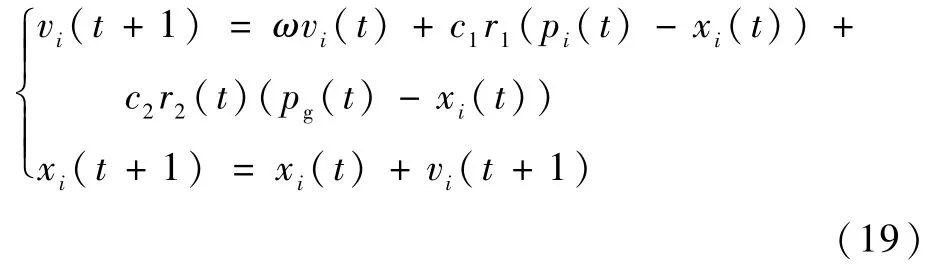
式中:t为当前迭代次数;r1、r2表示(0,1)之间的随机数;c1、c2为加速因子,一般在(0,4)之间取值;ω为惯性权重;xi为粒子位置;vi为粒子速度函数;pi为个体极值;pg为全体极值。

3.2 PSO算法优化隶属度函数

模型以装载机典型的工作周期实际载荷功率作为模糊逻辑控制器的输入之一。本文使用已知控制规则优化隶属函数的优化方法[20],在仿真系统中代入实际的模糊控制器。超级电容的SOC值应该保持在一定的范围内,约束条件如下:

复合电源中放电功率约束为:在装载机行驶过程中,复合电源系统的放电功率要受到其自身功率的限制,约束条件如下:

粒子群优化目标是降低燃料电池汽车在整个运行工况的总等效氢耗,即

式中:MFC为燃料电池耗氢量;MSC当超级电容等效耗氢量。

将输入输出中所有的隶属度函数进行优化,隶属函数通过PSO优化算法迭代了474次后保持不变,并达到最大适应度1。将输入输出中所有的隶属函数优化后代入到新的模糊逻辑控制器中进行观测。优化前后模糊逻辑规则对比观察器如图20所示,选则观测器片段,提取Pdem=106kW,超级电容SOC=0.659时刻数据,通过优化后燃料电池输出功率为PFC=58.3kW。与原观察器相比,燃料电池输出功率下降0.7kW。

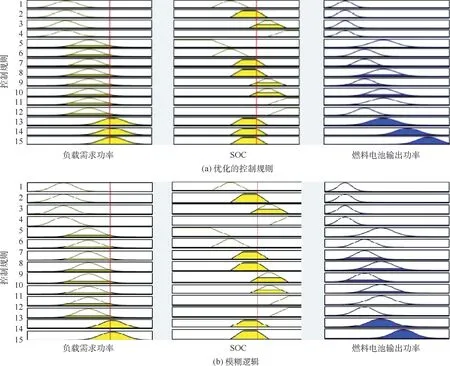
图20 优化前后的模糊逻辑规则观察器(部分)Fig.20 Rule observer before and after fuzzy logic controller optimization(part)

4 PSO算法优化-模糊逻辑控制器仿真

以装载机同样工况周期的实际载荷功率曲线作为模糊逻辑控制器的输入,按照PSO算法优化的隶属度函数建立控制规则,通过控制模式对比仿真分析。

经过PSO算法优化控制器后,燃料电池输出功率对比曲线如图21所示。Haar小波处理代表通过3层Haar小波处理需求功率后进行模糊逻辑控制结果,PSO算法优化代表通过小波处理后并对模糊逻辑隶属度函数进行粒子群优化后的控制结果。在“波峰波谷”处清晰看到燃料电池输出功率波动较少,变化平缓,在满足装载机系统动力性要求的前提下,燃料电池输出平均功率同比下降5%左右,有效提高燃料电池的效率。因此,通过PSO算法优化模糊逻辑控制器对复合电源系统功率分配因子进行修正,有效平衡燃料电池系统在快速变载、频繁启停、过载等恶劣工况下的功率输出,提高燃料电池的使用寿命与系统的综合性能。满足装载机系统的动态工况需求,保证燃料电池工作状态变化更加平稳,兼顾系统的耐久性和经济性。

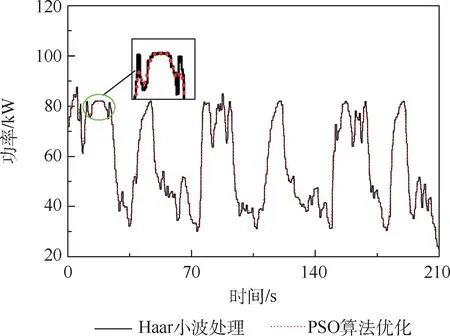
图21 优化后燃料电池输出功率变化曲线Fig.21 Output power curves of optimized fuel cell

如图22所示,经过优化后,选择在某单循环工况中重载频繁工况(35s)下研究超级电容平衡功率数据。通过3种控制模式进行对比仿真分析,图中原始数据代表未处理载荷谱数据进行模糊逻辑控制,Haar小波处理代表通过3层Haar小波处理需求功率后进行模糊逻辑控制,PSO算法优化代表通过小波处理并对模糊逻辑隶属度函数进行优化后的控制。超级电容输出功率中,原始数据曲线变化相对平滑,但Haar小波处理后,曲线变化幅度较大,PSO算法优化后,曲线变化频率与变化幅度最大。因此,在复合电源系统中,为了提高燃料电池的综合效率,利用超级电容吸收负载功率中混沌和暂态分量。

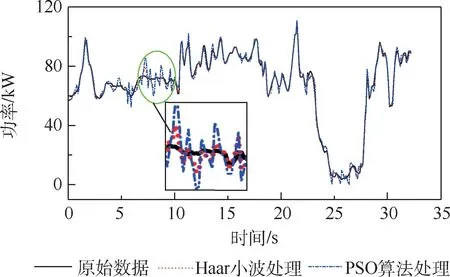
图22 优化后超级电容输出功率变化曲线Fig.22 Output power curves of optimized super capacitor

图23为超级电容在全周期工况下Haar小波处理与PSO算法优化后的SOC值变化曲线对比。优化后曲线变化幅度更剧烈,但超级电容SOC值保持在0.6左右,说明超级电容能够满足工况需求,优化后的控制器效果明显。

图23 优化后超级电容SOC变化曲线Fig.23 SOC curves of optimized supercapacitor

5 结 论

本文围绕复杂工况下燃料电池和超级电容复合电源式装载机进行控制策略研究,分析多系统耦合特征,探索分层优化控制的机理。首先,建立燃料电池复合电源装载机复杂工况下系统多状态模型;其次,基于Haar小波理论分层处理载荷功率;然后,基于模糊逻辑控制策略探索复杂工况对系统耦合特性的影响规律;最后,基于PSO算法优化隶属度函数,探索复杂工况下系统功率分配及优化控制策略。通过仿真数据验证结论如下:

1)经过最优阈值3层Haar小波处理后,将需求功率进行分配,一些混沌和暂态分量用超级电容平衡,避免燃料电池处理急速变化的功率需求,有效提升燃料电池系统寿命与整车经济性。

2)提出模糊逻辑能量管理策略动态平衡需求功率,设计模糊逻辑控制器,制定控制规则,仿真结果显示,燃料电池功率变化平滑,提高了电源系统的效率,超级电容工作在设定区域内,工作功率变化幅度相对剧烈,控制策略合理。

3)经过PSO算法优化控制器后,燃料电池输出功率变化幅度变得更平缓,燃料电池平均功率同比下降5%左右。有效提高燃料电池的效率与耐久性。