冰雪天气下基于MFOA-KELM残差修正的跑道温度混合预测
2022-11-30陈斌刘悦李庆真丁宇王立文
陈斌,刘悦,李庆真,丁宇,王立文
(1.中国民航大学 电子信息与自动化学院,天津 300300; 2.中国民航大学 航空地面特种设备研究基地,天津 300300)
冬季机场跑道面临积冰、积雪的现象,由此常常会引发诸如航班延误、旅客滞留等问题。温度是导致跑道结冰的重要因素,对跑道温度进行短时精准预测会为跑道结冰预警提供有效信息,不仅可以提高航班运行安全裕度,还有助于机场及时采取除冰雪等应急措施,减少航班延误。
多年来,国内外对与跑道结构相似的路面温度开展了大量研究,常用的路面温度预测方法主要有统计回归法和理论分析法。统计回归法指对大量路面温度观测数据进行统计回归建模,如线性回归法[1]、时间序列法[2]等。统计回归模型简单,但需要大量实测数据,模型普适性低[3]。理论分析法是根据气象学和传热学基本原理采用数值分析方法建立的路面温度场预测模型[3]。Barbere[4]于1957年最先使用该方法,利用路面介质温度周期变化热传导方程来描述路面温度演变规律。此后,国内外学者对该方法不断进行改进。Christison[5]、严作人[6]等以气温和太阳辐射为边界条件,基于层状路面热传导方程,通过有限差分等数值方法求解,建立了沥青路面温度预测模型。Hu等[7]根据空气温度、湿度、风速等环境因素建立了基于能量平衡和热传导方程的路面温度预测模型。Nuijten[8]基于能量守恒方法,综合考虑辐射通量、风速等和跑道材料之间的能量平衡关系,建立了跑道温度预测模型。机理模型能够从本质上反映气象、环境和路面结构材料对路面温度场的影响机理,不需要大量实测数据,普适性较强[3],被广泛应用于路面温度预报中[9]。然而在实际运行的机场中,使用机理模型预测时,起降飞机的尾流[8]、除冰液稀释前后释放的热量会使道面温度受到瞬时冲击[10]。除冰雪前后的道面覆盖物状况、除冰雪作业方式等多种因素都会影响机理模型热通量参数的确定,使导热微分方程在求解时需要多种假设简化解析表达式和边界条件[11],这将影响机理模型对道面温度的预测准确度。另外,机理模型的有限差分求解与离散化,当预测时长增加时导致的误差累积问题也不容忽视。
为了解决机理模型的上述缺陷,学者们分别从机理和数据分析角度进行误差补偿。基于数据分析的误差补偿方法在电力、化工、软测量领域应用广泛。姚源朝等[12]利用广义回归神经网络(generalized regression neural network,GRNN)补偿了气流床汽化炉机理模型的预测残差,建立了结合机理与GRNN的混合预测模型,但GRNN模型需要通过选择合适的目标函数才能平衡参数平滑因子。成庶等[13]使用支持向量机完成了对电容器寿命预测的补偿修正,然而支持向量机在处理规模大的数据样本时,运行速度慢,需要大量的计算时间。核极限学习机(kernel extreme learning machine,KELM)是一种具有强大泛化能力和非线性拟合能力的数据驱动方法,结构简单,运行速度快[14],但是其预测性能受到正则化参数和核函数参数的影响[15]。果蝇优化算法(fruit fly optimization algorithm,FOA)计算简单、调整方便,能够解决KELM参数自动优选的问题[16]。目前,FOA和KELM相结合的方法已经应用于医疗、金融等领域。Mythili和Kumar[17]将FOA-KELM用于解决高维基因特征选择问题;王东[18]提出一种FOAKELM核参数的时间序列预测方法。但FOA易陷入局部极小值,出现早熟收敛等情况[19]。
因此,本文提出了一种基于改进FOA(modified fruit fly optimization algorithm,MFOA)优化KELM(MFOA-KELM)的跑道温度混合预测模型。首先,通过简化边界条件建立跑道温度机理预测模型;然后,利用KELM强大的非线性拟合能力使机理预测残差最小化,并利用MFOA寻找KELM的最佳参数组合;最后,实现跑道温度短时预测。
1 机理预测模型
1.1 跑道边界条件
跑道结构处于外界自然环境中,受到周围多种环境因素的综合作用,如太阳辐射、降雨、降雪或起降航班等[20]。跑道温度的变化往往以影响因素热量流动的形式在跑道温度场中传导。跑道热量传导过程如图1所示。综合考虑各影响因素热通量,基于能量守恒定律,可得跑道温度机理预测模型的边界条件[21]如下:

图1 跑道热量传导过程示意图Fig.1 Schematic diagram of runway heat transfer process
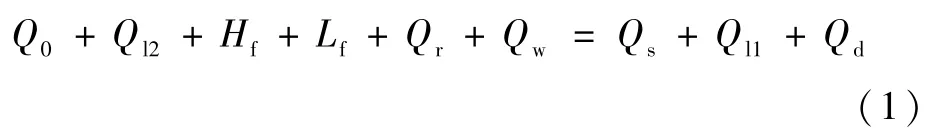
式中:Q0为道面热通量;Qs为太阳短波辐射通量;Ql1为大气长波辐射通量;Ql2为道面长波辐射通量;Hf为感热通量;Lf为潜热通量;Qr为降雨热通量;Qw为降雪热通量;Qd为航班密度热通量。
1)太阳短波辐射通量Qs。其计算式为
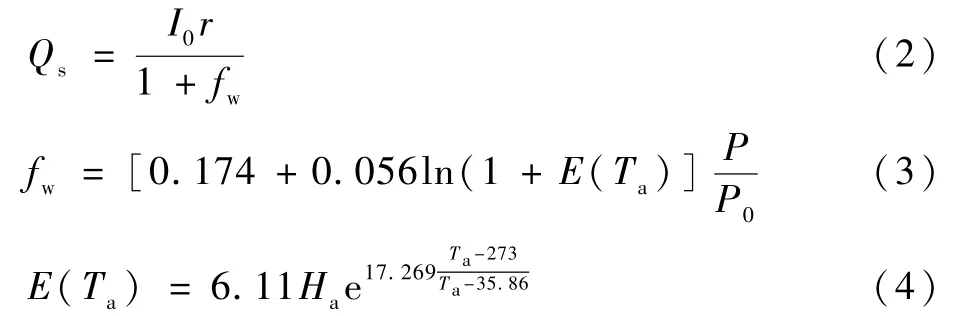
式中:I0为太阳常数;r为跑道对太阳辐射的吸收率;fw为大气层对太阳辐射的削弱系数;Ta为大气温度;P、P0分别为大气压强、标准大气压强;Ha为大气相对湿度。
2)长波辐射通量Ql1、Ql2。其计算式为

式中:σ为玻尔兹曼常数;T0为跑道温度;εa、εr分别为大气相对辐射率、道面相对辐射率。
3)感热、潜热通量Hf、Lf。其计算式为
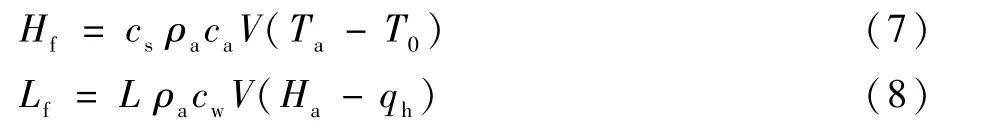
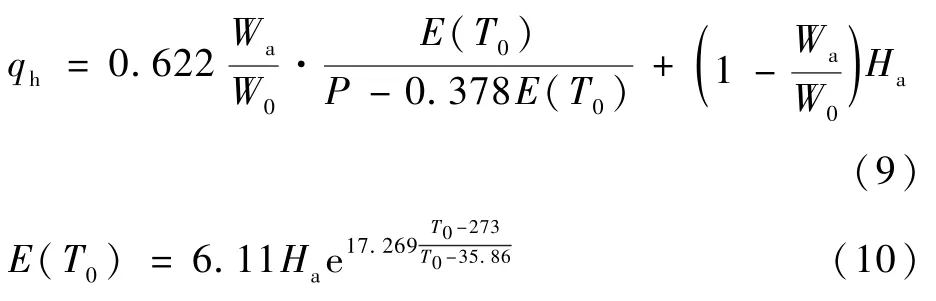
式中:cs为感热传输系数;ρa为跑道附近空气密度;ca为空气比热容;V为风速;L为凝结潜热;cw为水汽传输系数;qh为道面比湿;Wa为机场道面吸水量;W0为机场道面饱和吸水量,取值范围为0<Wa/W0<0.5。
4)降雨、降雪热通量Qr、Qw。其计算式为
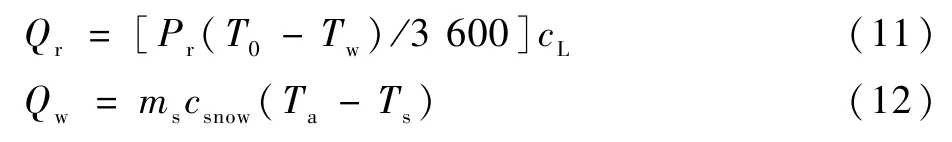
式中:Pr为降雨速率;Tw为水膜温度;cL为水的比热容;ms为雪的质量通量;csnow为雪的比热容;Ts为雪的温度。
5)航班密度热通量Qd。航班密度热通量指飞机尾流与跑道之间的热通量,取决于航班密度N、飞机起降时间ta和飞机尾流在跑道上方产生的温度幅值ΔT,其计算式为

式中:λ为跑道的导热系数。
飞机在起降时,飞机尾流在跑道上方升高的温度,取决于飞机的型号和推力。本文以波音737-800机型为例,通过计算飞机在最佳推力下起飞时的燃油消耗量,获得飞机尾流对跑道上方空气产生的温度幅值ΔT,其计算式为
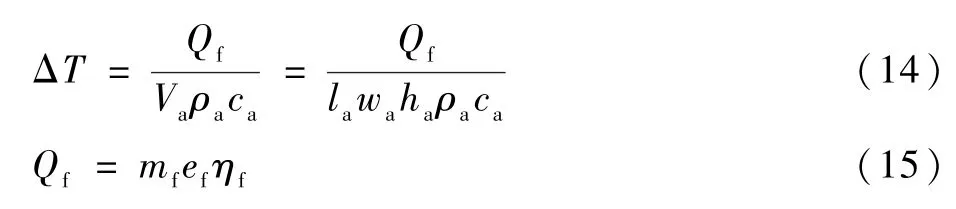
式中:Qf为燃油燃烧释放能量;la和wa、ha分别为起飞距离和受影响空气的宽度、高度;ηf为燃料燃烧效率;ef为燃料能量密度;mf为燃料使用量;Va为受到飞机尾流影响的空气体积。
波音737-800起降时的参数如表1所示[8]。

表1 波音737-800起降参数[8]Table1 Taking-off and landing parameters of Boeing737-800[8]
1.2 跑道温度机理预测模型
跑道温度预测的本质是求解复杂边界条件下跑道温度的导热微分方程。由于跑道为层状结构[22],本文建立一维跑道导热方程,其结构为
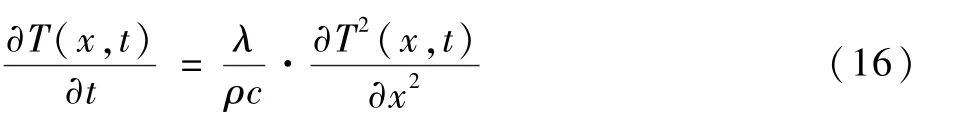
式中:t为时间;x为空间坐标;ρ为跑道材料密度;c为跑道材料比热容;T(x,t)为当时间为t时,地基深度为x的跑道温度。
联立式(1)、式(16),通过有限差分法网格划分,由差商近似表示微商[23],可得跑道温度机理预测模型为

式中:i为当前时刻,i+1为下一时刻;Tm为跑道温度机理预测模型预测值;T1为跑道下方深度为h处的温度值;τ为网格划分时间步长;Q0(i)为i时刻跑道与外界环境交换的热通量,Q0(i)=Qs(i)+Ql1(i)+Qd(i)-Ql2(i)-Hf(i)-Lf(i)-Qr(i)-Qw(i)。
2 基于MFOA-KELM残差修正的混合预测模型
2.1 核极限学习机基本原理
KELM引入核函数代替ELM隐含层节点的特征映射,不需要设置隐含层节点数目、初始权值和偏置,综合考虑经验风险和结构风险[24],根据KKT(Karush-Kuhn-Tucker)最优化条件,确定网络输出权值φ为
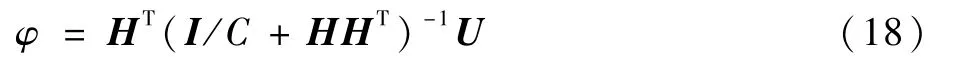
式中:I为单位对角矩阵;C为正则化参数,用于平衡经验风险和结构风险的分配;H为将输入映射到隐含层的特征向量;U为期望输出向量。
由此,获得KELM输出函数表达式为

定义核函数表达式为
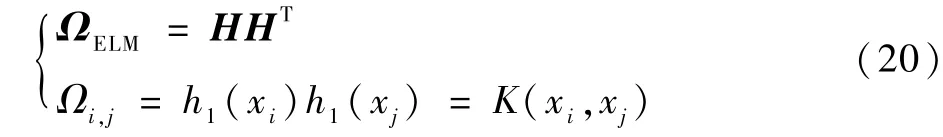
式中:K(xi,xj)为核函数。
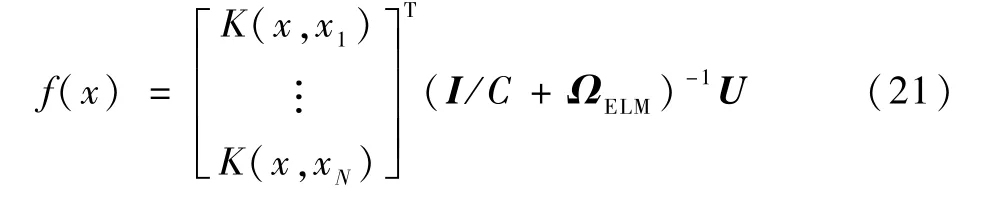
则式(19)变换为核函数的选择有很多,考虑到径向基(radial basis function,RBF)核函数参数设置较少,故本文选用RBF核函数,定义为
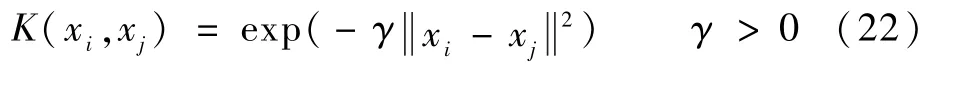
2.2 改进的果蝇优化算法
2.2.1 果蝇优化算法的改进方法
FOA是一种基于果蝇觅食行为寻找全局最优解的群体新智能算法[16],但其在迭代寻优过程中会出现以下问题:果蝇的搜索步长RandomValue为固定在区间[0,1]之间的随机值,搜索步长过小会使果蝇个体收敛速度变慢,不能全局充分搜索,易陷入局部最优解。因此,为避免FOA陷入局部极值,提高果蝇的全局寻优能力和计算效率,本文采用以下方法对FOA进行改进:①采用权值更新函数w1更新果蝇个体的搜索步长,使搜索步长不再是局限于一定范围内的随机值,平衡了果蝇的局部寻优能力和全局寻优能力。②引入距离扩充因子d计算味道浓度判定值Si,扩充了Si的解空间范围。
MFOA迭代寻优步骤如下:
步骤1设置果蝇种群规模sizepop,最大迭代代数maxiteration,果蝇个体的随机初始位置X_axis、Y_axis。
步骤2更新果蝇个体的移动位置。利用权值更新函数更新果蝇个体利用嗅觉寻找食物的距离。

式中:w0为初始权值;β为权值系数;g为果蝇当前迭代代数;Xi、Yi为果蝇个体的更新位置;RandomValue为区间[0,1]之间的随机数。
步骤3计算果蝇味道浓度判定值Si。此时果蝇的味道浓度判定值Si为果蝇个体到原点距离的倒数与距离扩充因子d之和。
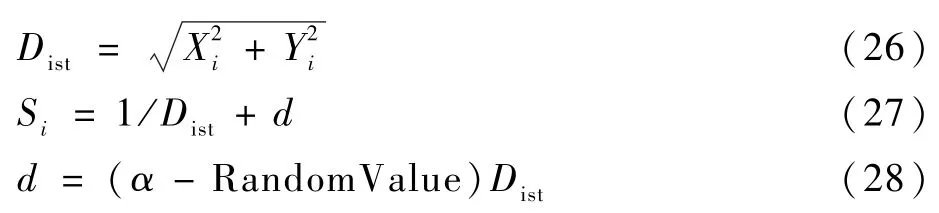
式中:Dist为果蝇个体到原点的距离;α为常数。
步骤4更新果蝇群体位置,获得最佳味道浓度Smell(i)。将味道浓度判定值Si代入味道浓度判定函数(适应度函数)中,可得到每只果蝇个体位置的味道浓度值,通过对比获得果蝇群中味道浓度最佳的果蝇个体。
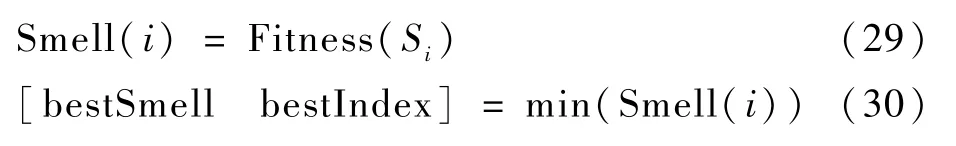
式中:Fitness为味道浓度判定函数(适应度函数);[bestSmell bestIndex]为果蝇群中味道浓度最佳的果蝇个体。
步骤5保留最佳味道浓度值和x、y坐标,果蝇群将以最佳浓度个体为目的地前往飞行。
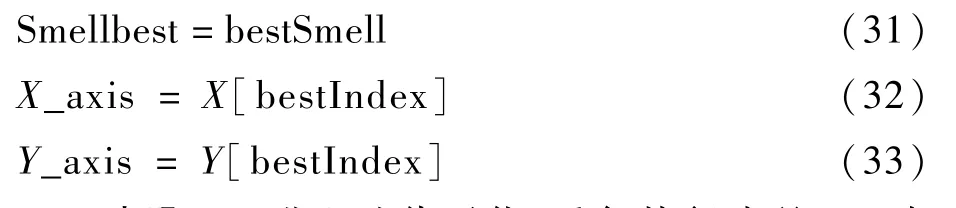
步骤6进入迭代寻优,重复执行步骤2~步骤5,判断味道浓度是否优于前一迭代,若是则迭代停止。
2.2.2 改进的果蝇优化算法性能评估
为验证MFOA的有效性与优越性,选用4个标准测试函数对MFOA进行仿真测试,并与FOA、粒子群优化算法(PSO)和差分进化算法(DE)对比。测试函数的表达式、自变量的搜索区间和理论最优值如表2所示[25]。其中,F1、F2为单峰函数,F3、F4为多峰函数,使用单峰函数来验证算法的收敛速度,使用多峰函数来验证算法跳出局部最小值的能力[26]。

表2 标准测试函数[25]Table2 Standard test functions[25]
为了运算的公平性,实验选取相同的共性参数,设置种群规模为80,迭代次数为300,对每一种测试函数独立运行30次,测试函数的维数为30。在MFOA中,设置w0=0.8,β=1.1,α=0.5。PSO算法的参数设置详见文献[27]。DE算法的参数设置详见文献[28]。选用各算法对测试函数最佳求解结果的平均值和标准差作为评价优化算法的性能指标,如表3所示。图2为MFOA和FOA对4种测试函数的适应度曲线。
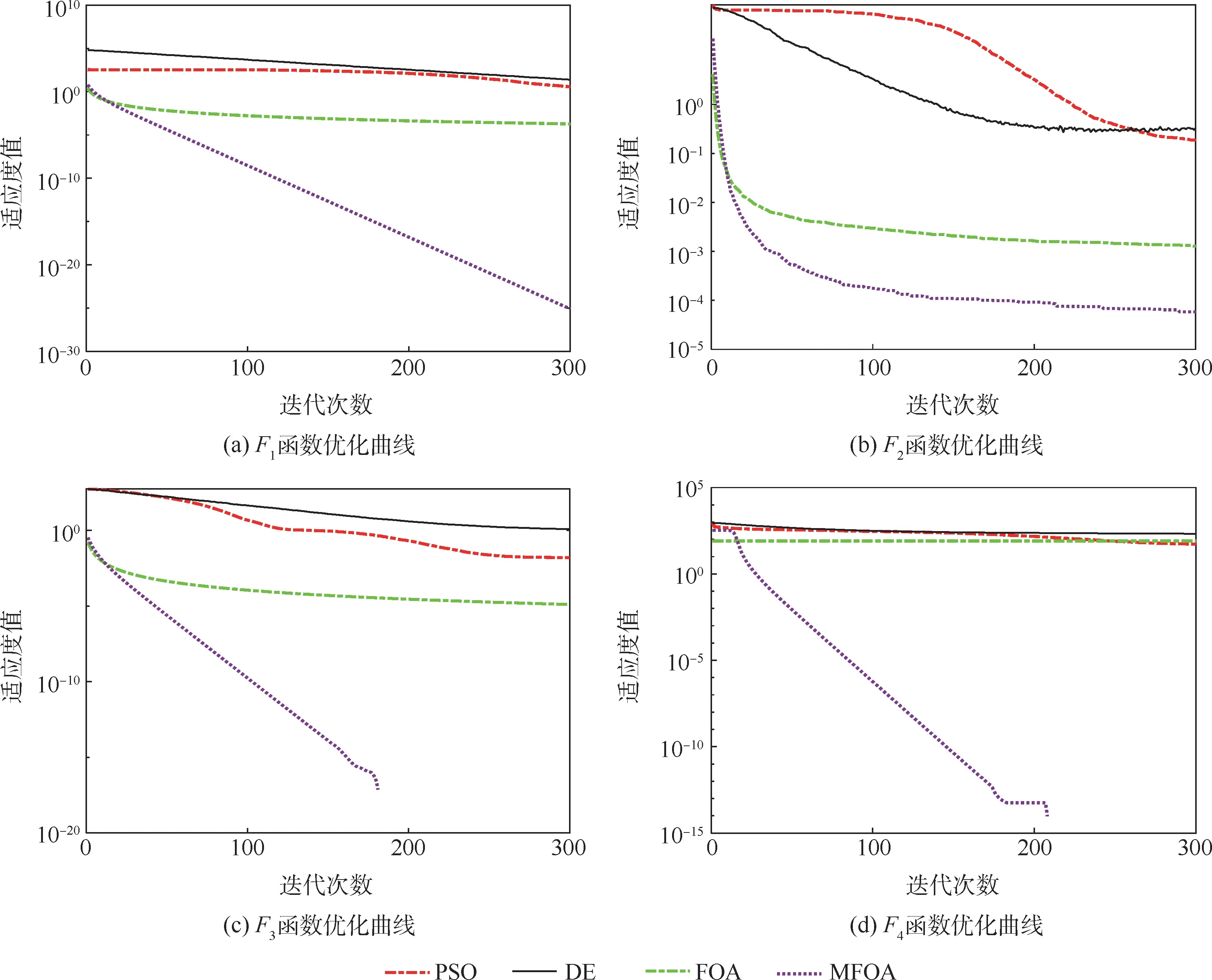
图2 函数优化曲线Fig.2 Function optimization curves
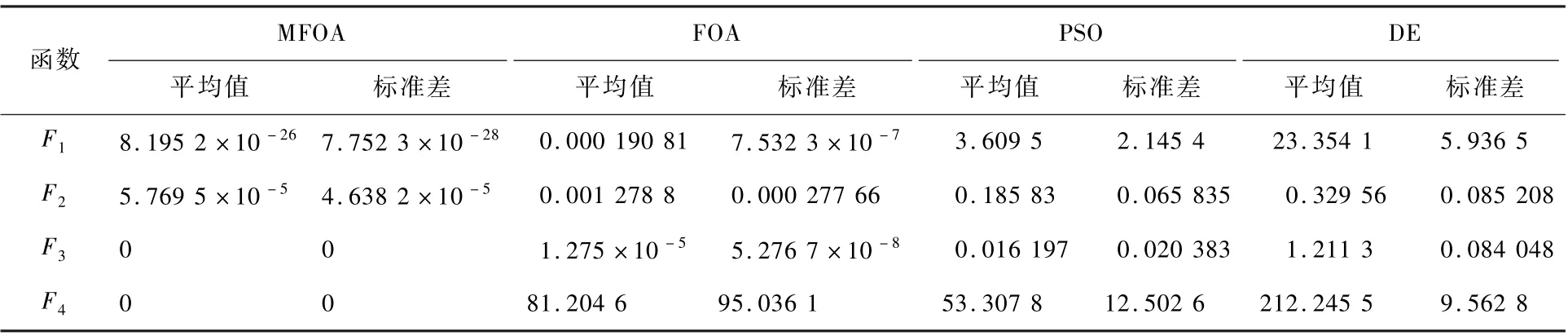
表3 优化结果比较Table3 Optimization result comparison
由表3可见,在4个测试函数的寻优结果中,与FOA、PSO、DE算法相比,MFOA均能求得最小的平均值和标准差,且在F3、F4测试函数中可以稳定求出全局最优解。由图2可见,在4个测试函数中,与FOA、PSO、DE算法相比,MFOA收敛速度更快,寻优精度更高。对于F3、F4多峰测试函数,MFOA分别在迭代次数为182次和209次时就达到了最优适应度值0。可见,MFOA具有更强的局部搜索能力和全局寻优能力。
2.3 基于MFOA-KELM残差修正的混合预测模型建模
2.3.1 混合预测模型的构建
在跑道温度混合预测模型中,以机理预测模型为基础预测模型,综合考虑跑道与其周围太阳短波辐射通量、潜热通量、航班密度等热通量之间的能量流动,基于传热分析从跑道结构特性和交通状况角度预测跑道温度。利用MFOA-KELM预测机理预测模型的残差,对机理预测模型预测值进行补偿修正。
基于MFOA-KELM残差修正的混合预测模型结构如图3所示。具体预测步骤如下:
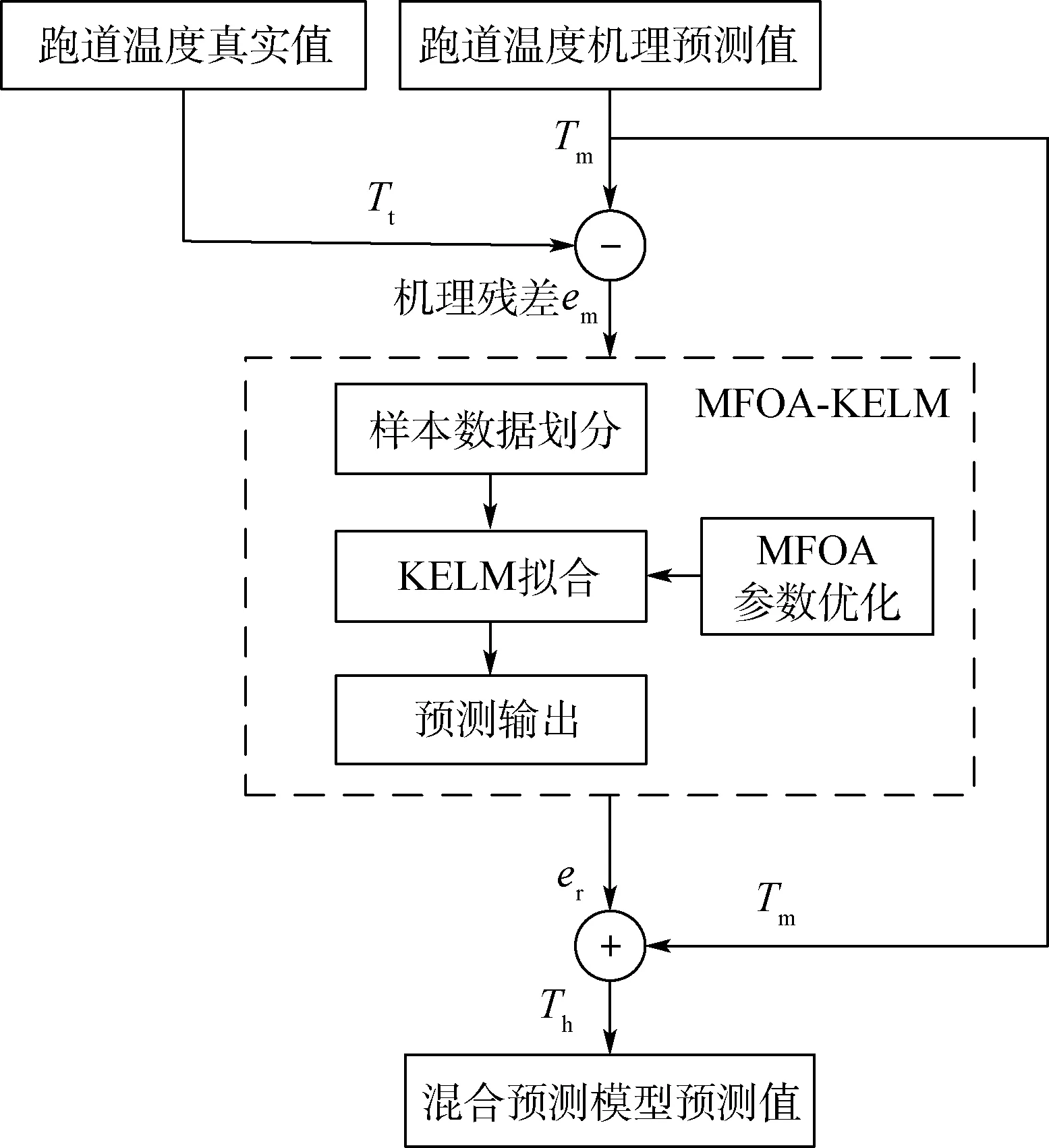
图3 混合预测模型结构Fig.3 Structure of hybrid prediction model
步骤1使用机理预测模型预测跑道温度,获得机理预测模型预测值Tm与机理预测模型残差值em。
步骤2建立MFOA-KELM模型,用于预测机理预测模型的残差,获得机理预测模型残差预测值er。
步骤3将步骤2预测的残差预测值er与机理预测模型预测值Tm进行叠加,获得混合预测模型预测值Th。

2.3.2 基于MFOA-KELM的机理残差预测
KELM具有强大的非线性拟合能力,能够根据跑道周围多影响因素与机理预测模型残差之间的数据关系建立非线性映射,预测下一个时刻机理预测模型的残差值。但KELM的预测性能与其内部正则化参数C与核函数参数γ密切相关。因此,本文采用MFOA对KELM进行参数寻优,建立MFOA-KELM修正模型。具体预测流程如图4所示。
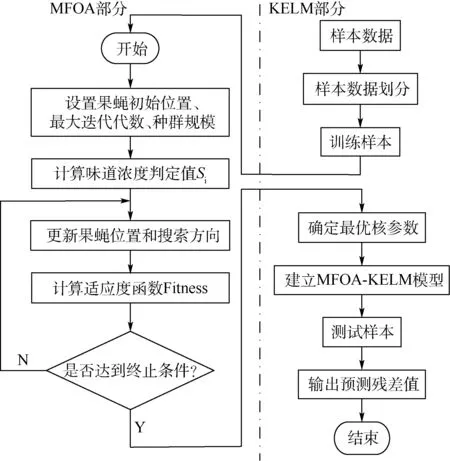
图4 MFOA-KELM模型流程Fig.4 Flow chart of MFOA-KELM model
将机理残差值em作为MFOA-KELM模型的输出部分,将跑道周围多影响因素——气温、大气湿度、风速、大气压强和道面下方深度为h处的温度作为MFOA-KELM模型的输入部分。设置果蝇种群的初始参数,以训练样本的均方误差作为果蝇参数寻优的适应度函数。适应度函数的计算表达式为
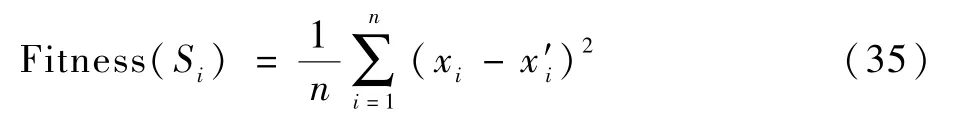
式中:xi为第i个预测点的实际值;x′i为第i个预测点的预测值;n为预测点个数。均方误差越小,表示寻优个体的适应度值越好,MFOA-KELM模型预测的机理残差值越准确。当KELM模型获得最优正则化参数C和核函数参数γ时,迭代停止,输出机理预测模型残差预测值er。
3 实例验证
3.1 数据来源
为验证本文所提的混合预测模型对冰雪天气下跑道温度预测的可行性,笔者于2019年12月23日至2020年1月7日在模拟跑道温度实验平台中采集实验数据,实验平台如图5所示。模拟跑道道面为根据MH∕T5004—2010[29]设计的水泥混凝土道面。采用ARS31Pro道面传感器、Vaisala wtx520气象传感器、湿度传感器、PT100温度传感器依次测量风速、气温、大气湿度、大气压强和道面下10cm深度处温度。选取表4中4组实验数据样本建模预测。在每组样本中选取前10个小时数据为输入样本集,以每分钟样本输入数据的未来15min,30min,60min,120min温度为样本输出集。将每组样本的前80%数据作为训练集用于构建模型,后20%数据作为测试集用于模型验证。其中,样本1为持续性降雪天气,最低气温-0.38℃,最高气温0.6℃。样本2~样本4为阴天天气,最低气温依次为-2.31℃、-1.64℃、-1.3℃,最 高 气 温 依 次 为3.87℃、1.4℃、3.6℃。
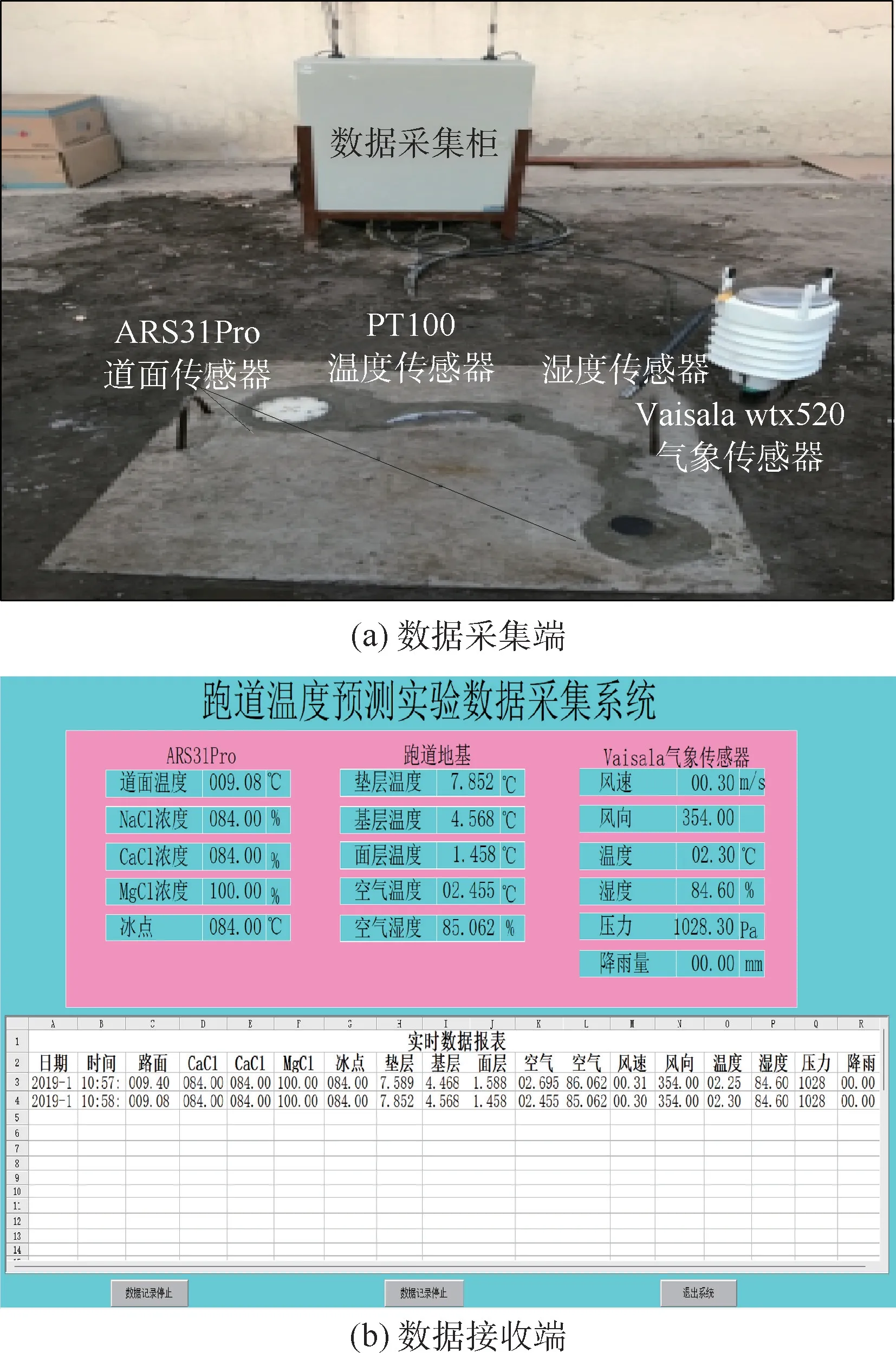
图5 模拟跑道温度实验系统采集平台Fig.5 Simulation of runway temperature experimental system collecting platform
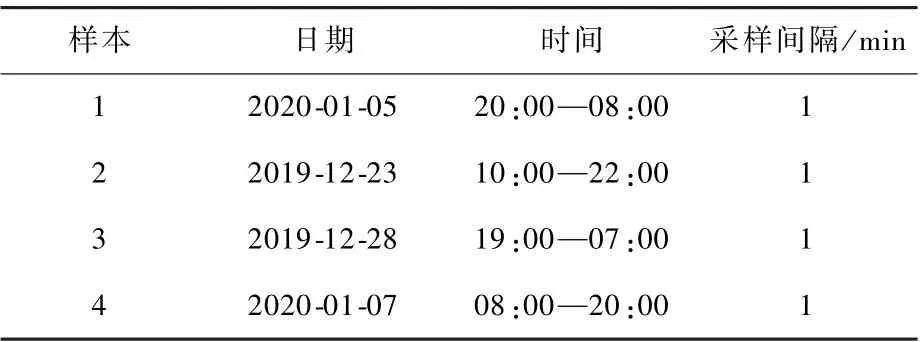
表4 实验数据样本Table4 Experimental data samples
3.2 数据归一化
在MFOA-KELM预测机理预测模型残差时,为了避免各跑道温度影响因子由于量纲不同对模型预测精度产生影响,将样本数据归一化到[0,1]区间。

式中:xmin为样本数据最小值;xmax为样本数据最大值;xi、x1分别为样本数据归一化前、后的数值。
3.3 模型评价指标
选取平均绝对误差(MAE)和平均预测准确率(ACC)对混合预测模型预测准确性进行评价分析[30-31]。MAE数值越小,ACC数值越大,表示模型预测越准确。计算公式如下:
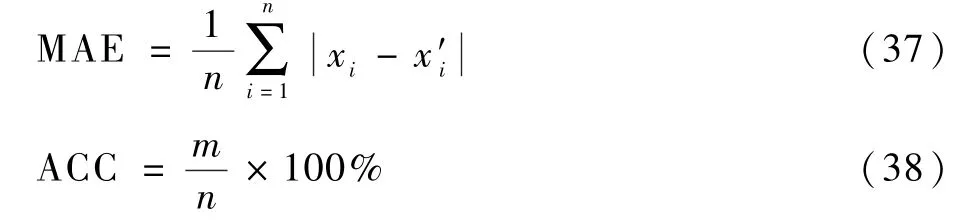
式中:m为预测残差在规定残差阈值内点的个数。
3.4 混合预测模型预测结果及分析
3.4.1 模型参数设置
机理预测模型相关参数设置如表5所示。表中:cr为跑道结构材料比热容。设置FOA种群规模为10,迭代代数为100,优化参数个数d1=2,正则化参数C与核参数γ的取值范围分别为[0,10]和[0,100],其他参数设置与2.2.2节相同。对训练样本以均方误差最小为优化目标,得到MFOA-KELM预测残差值,将其与跑道温度机理预测模型预测值叠加获得MFOA-KELM混合预测模型预测值。为充分验证MFOA-KELM混合预测模型的有效性,分别与FOA-KELM、KELM混合预测模型预测值对比,选取相同的数据进行预测。

表5 机理预测模型参数Table5 Mechanistic prediction model parameters
3.4.2 预测结果及模型误差对比分析
上述3种混合预测模型与单一机理预测模型的预测结果如图6所示,平均绝对误差如表6所示。图6中,每组样本的机理预测模型预测值表明,预测时长越短,机理残差越小,随着预测时间延长,预测残差不断增大。机理预测模型会随着预测时长的增加不断累积误差。在表6中,当预测同一时长时,机理预测模型的平均绝对误差最大。随着预测时长增加,MFOA-KELM混合预测模型均具有最小的平均绝对误差值。当预测时长为120min时,与机理预测模型、FOAKELM混合、KELM混合预测模型相比,MFOAKELM混合预测模型的平均绝对误差分别至少减小了61.43%、20.16%和26.80%。可见,引入权值更新函数和距离扩充因子的MFOA,增强了果蝇种群对正则化参数C与核函数参数γ的全局寻优能力,能够获得更小的适应度函数值,提升了MFOA-KELM模型对机理残差的预测水平,进而使MFOA-KELM混合预测模型具有更好的预测准确性。
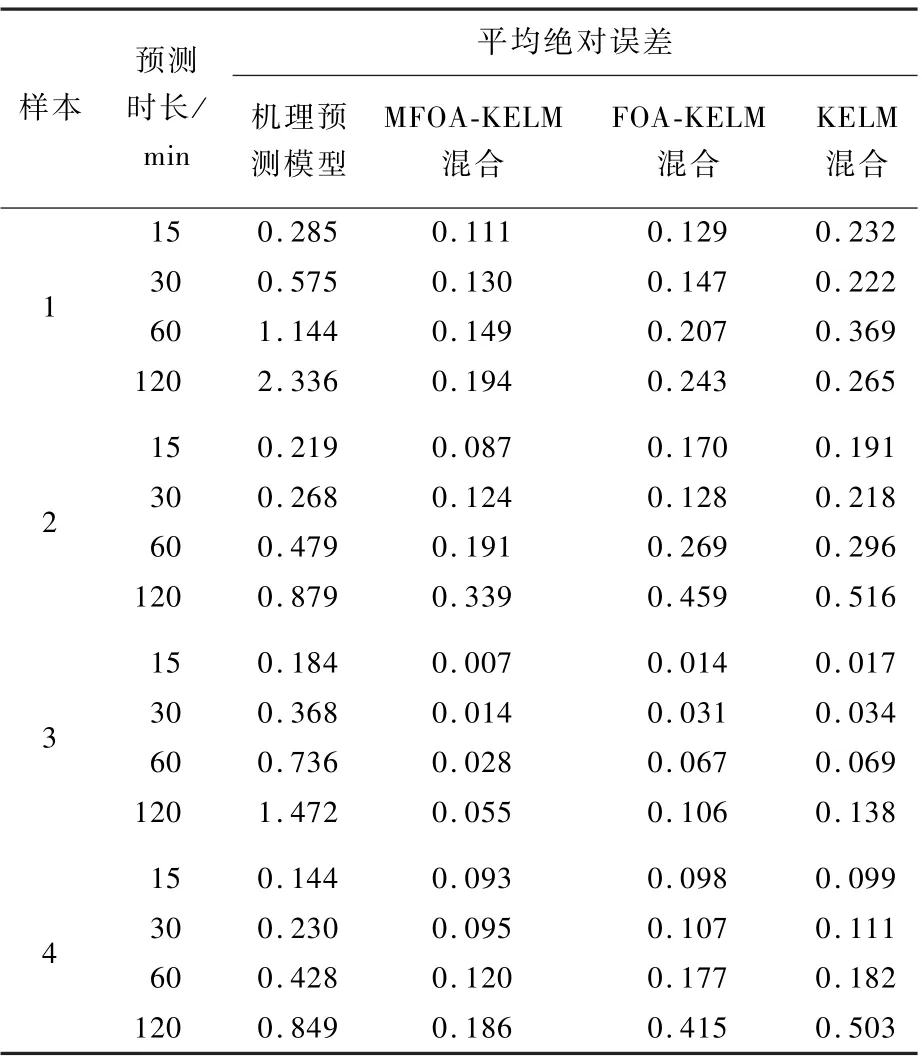
表6 样本1~样本4的平均绝对误差Table6 Mean absolute error of samples1,2,3and4
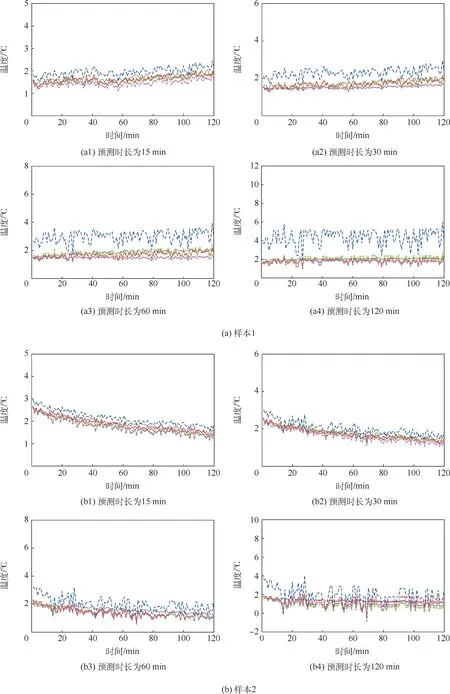
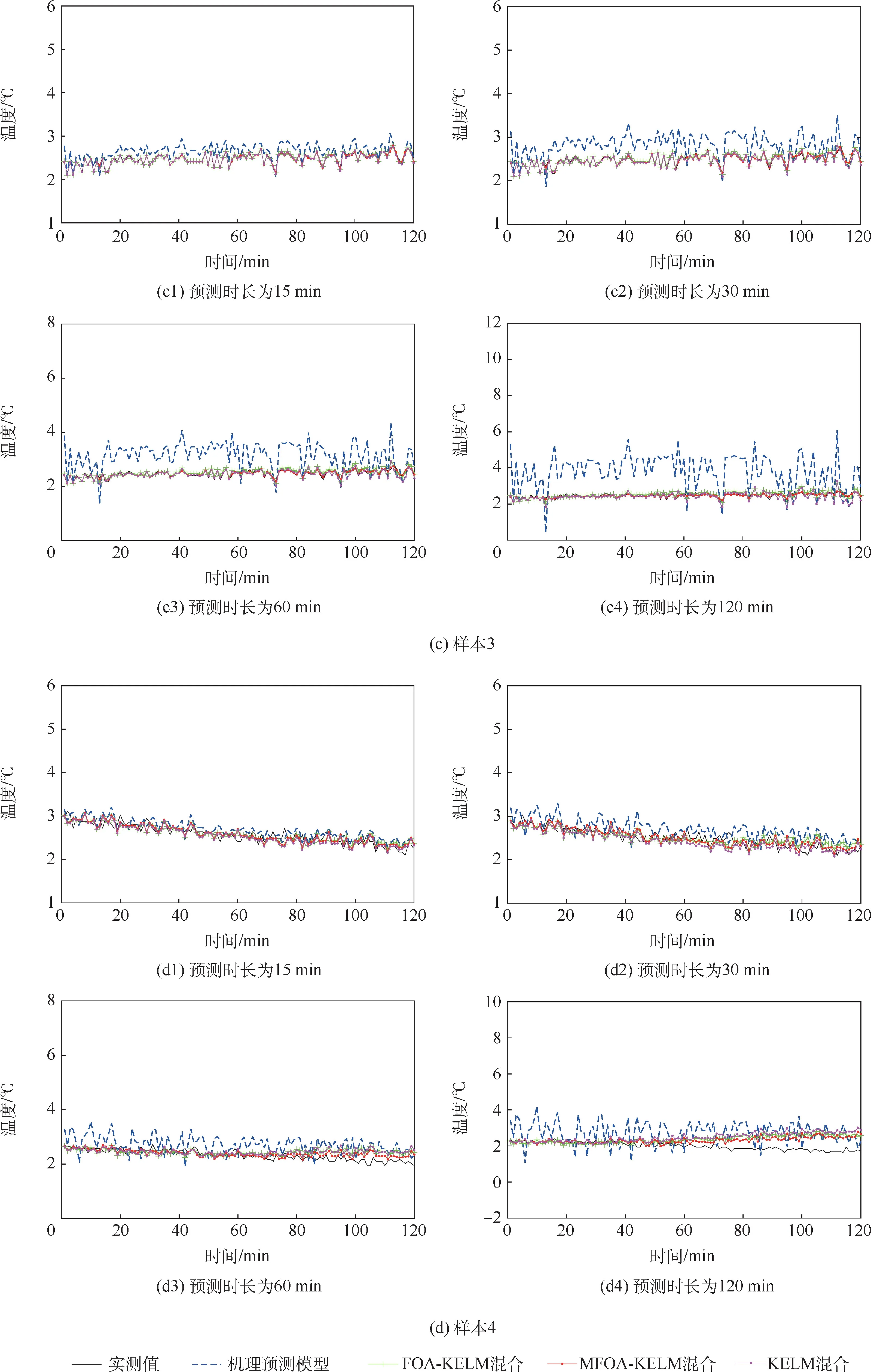
图6 样本1~样本4的预测结果Fig.6 Prediction results of samples1,2,3and4
3.4.3 模型准确率对比及分析
表7为4组样本数据在不同残差阈值内(±0.5℃,±1℃,±2℃)的平均预测准确率。可见,当残差阈值为±0.5℃时,在同一预测时长下,MFOA-KELM混合预测模型的预测准确率明显高于机理预测模型。在不同预测时长下,MFOAKELM混合预测模型的平均预测准确率同为最高。当预测时长为120min时,在3种残差阈值下,MFOA-KELM混合预测模型的平均预测准确率至少达到91.25%。可见,与单一的机理预测模型相比,MFOA-KELM混合预测模型利用KELM强大的非线性拟合能力能够充分挖掘道面温度影响因素,如气温、大气湿度、风速、地基温度等与道面温度机理预测残差之间的内部信息,由MFOAKELM混合预测模型预测的残差值补偿了机理预测模型预测值与跑道温度真实值之间的偏差,使MFOA-KELM混合预测模型比单一机理预测模型具有更高的预测准确率。

表7 不同残差阈值内平均预测准确率Table7 Average prediction accuracy under different residual threshold values
4 结 论
1)为提高FOA的收敛精度,避免算法出现早熟收敛的现象,本文通过引入权值更新函数和距离扩充因子来改进算法,避免原始算法陷入局部极小值。对4个标准测试函数进行仿真实验,将MFOA与FOA、其他群体智能算法进行比较,实验结果表明,本文提出的MFOA具有更高的收敛性能和全局寻优能力。
2)建立基于MFOA-KELM残差修正的跑道温度混合预测模型,以实测数据验证了该混合方法对跑道温度预测的有效性和泛化性。与单一机理预测模型相比,当预测时长为120min时,MFOA-KELM混合预测模型的平均绝对误差至少减小61.43%,预测准确性更高。
本文混合预测模型能够为跑道积冰预警提供有效信息。后续研究中将把跑道温度混合预测值作为跑道结冰预测的目标温度值,进一步展开对跑道结冰预测的研究。
