高超声速飞行器命中精度高准确度评估
2022-11-30彭维仕
彭维仕
(武警工程大学 装备管理与保障学院,西安 710086)
高超声速飞行器具备快速打击、攻击广泛、突防力强和毁伤较高的特点,在未来信息化条件下的局部战争中具有非常广阔的应用前景[1]。但是,高超声速飞行器的研制过程具备技术先进、耗资巨大、周期长等特点,导致其试验和验证评估非常困难。因为常规武器的评估方法可能无法满足高超声速飞行器高准确度的评估,所以亟需研究新理论和新方法以解决高超声速飞行器中的评估难题。
目前,关于高超声速飞行器的评估研究主要集中在某一个关键部件的性能评估,并且大多只给出了评估结果,并没有分析评估结果的可信度。例如,为了保证高超声速飞行器研制方案的科学性和合理性,文献[2]提出了通过性能数据库评价空对空飞行器的性能。为了分析高超声速拦截飞行器的气动设计特点,文献[3]提出了一种性能分析方法。为分析高超声速拦截飞行器的气动设计特点,文献[4]出了一种性能分析方法。为了选择最优的高超声速飞行器设计方案,文献[5]提出了基于TOPSIS和综合效用函数法的高超声速飞行器多学科设计优选方法,但在计算权重时采用了主观赋权法,大致评估结果存在一定的误差。进一步,为了选取最优的高超声速飞行器弹道优化方法,文献[6]提出了一种基于灰色关联度分析理论的高超声速飞行器弹道优化算法的综合评估方法,通过层次分析法(analytic hierarchy process,AHP)确定指标权重,并利用灰色关联度法确定被估系统与理想系统的“距离”,最终得到各方案的优劣排序。为了分析高超声速飞行器控制性能指标中底层指标能否反映高超声速飞行器的飞行性能,文献[7]提出了一种基于统计实验分析的检验方法,将可行性分析问题转化为特定映射的双映射检验问题,通过可行域的实验点数判定方案的可行性。为了解决高超声速飞行器制导控制系统性能评估中评估效率低的问题,文献[8]提出了基于优化拉丁超立方试验设计方法的高超声速飞行器制导控制系统的性能评估方法,利用优化拉丁超立方试验设计方法采用较少的采样次数以充满空间,进而提高评估的效率。针对评估中使用确定数值来表征评估数据时,无法准确反映评估数据的不确定性和模糊性的问题,文献[9]提出了一种基于区间数排序的目标威胁评估方法。为了验证高超声速飞行器的性能,文献[10]提出了基于模型迁移的方法,通过仿射相似度模型,建立了高超声速飞行器的模型。文献[11]通过构建高超声速飞行器再入控制方法的性能指标体系,结合AHP法和熵值法的各自优点,定量评估了高超声速飞行器再入控制系统的性能。在高超声速飞行器可信度评估方面,文献[12]提出了一种高超声速飞行器制导控制模型置信度评价方法,对高超声速飞行器系统模型进行校核,给出了该模型的置信度。
综上所述,现有高超声速飞行器性能评估方法在评估时仅给出了评估结果,未能给出该评估结果的可信度,无法准确评估高超声速飞行器的效能。因此,本文提出了一种基于误差谱的高超声速飞行器命中精度高准确度评估方法。该方法不仅能给出高超声速飞行器命中精度的评估结果,还能给出该结果的可信度。
1 高超声速飞行器命中精度数据预处理
由于高超声速飞行器属于小样本试验,经典的性能评估方法难以应用。针对小样本问题,通常利用重采样的方法对样本进行扩容,或者基于半实物仿真的方法对样本进行扩容等[13-15]。
如图1所示,以目标点为圆心O,构建坐标系XOZ。令(X,Z)=[(x1,z1),(x2,z2),…,(xn,zn)]为高超声速飞行器的命中精度试验数据(已通过相容性检验),其中,n为试验样本容量,并且试验数据满足独立同分布的条件。令目标位置为(X0,Z0)=(x0,z0),则横向和纵向偏差为
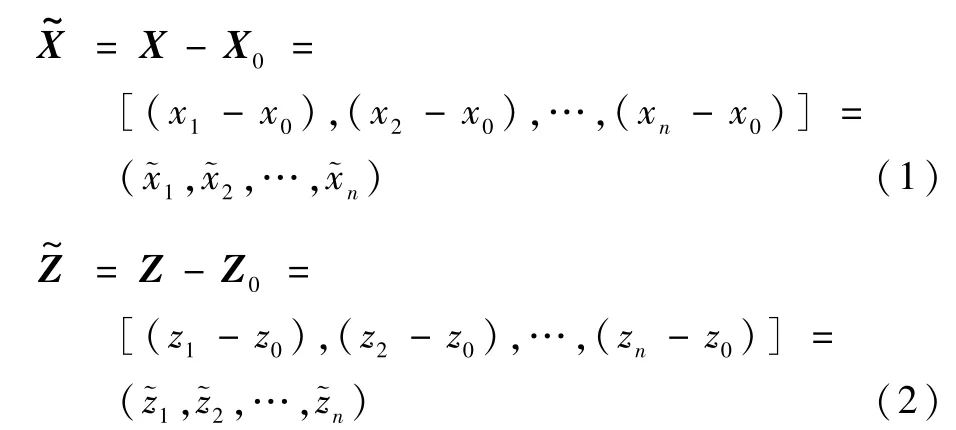
如图1所示,可得落点偏差为
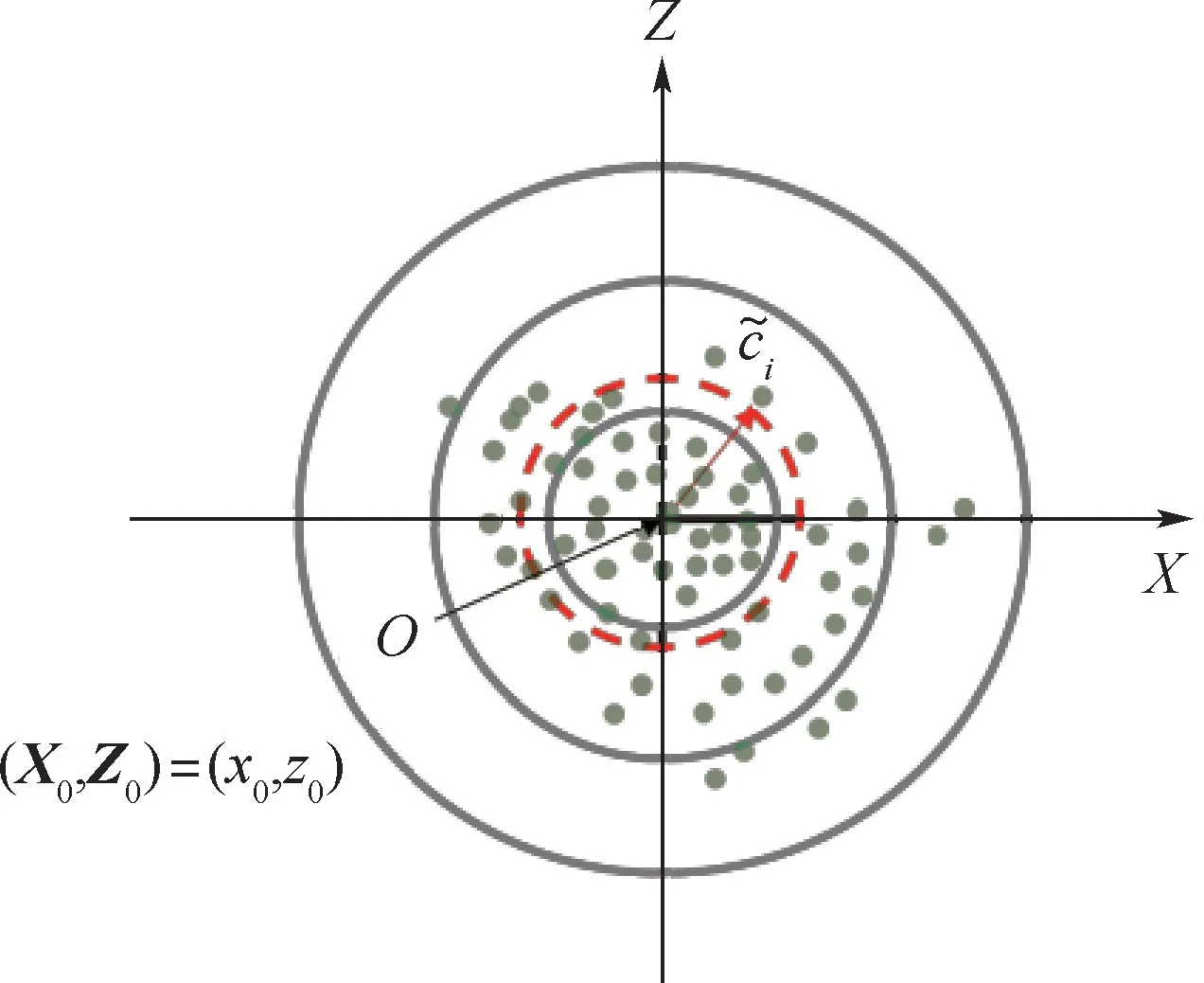
图1 落点偏差示意图Fig.1 Diagram of relative distance error
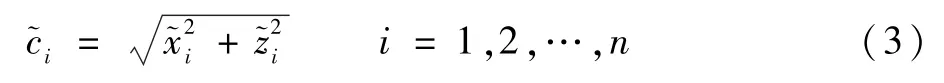
进一步,根据文献[14]中的扩容方法,对上述高超声速飞行器的原始数据进行扩容,其基本步骤如下:
步骤1随机产生一个服从均匀分布U(0,M)的正整数R,M满足M≫n。
步骤2令p=mod(R,n),其中,mod(·)表示求余函数,且当mod(R,n)=0时,令p=1;当mod(R,n)>n时,令p=n。

扩容后样本的落点偏差为

2 高超声速飞行器命中精度评估指标模型
2.1 算术平均误差和均方根误差评估指标模型
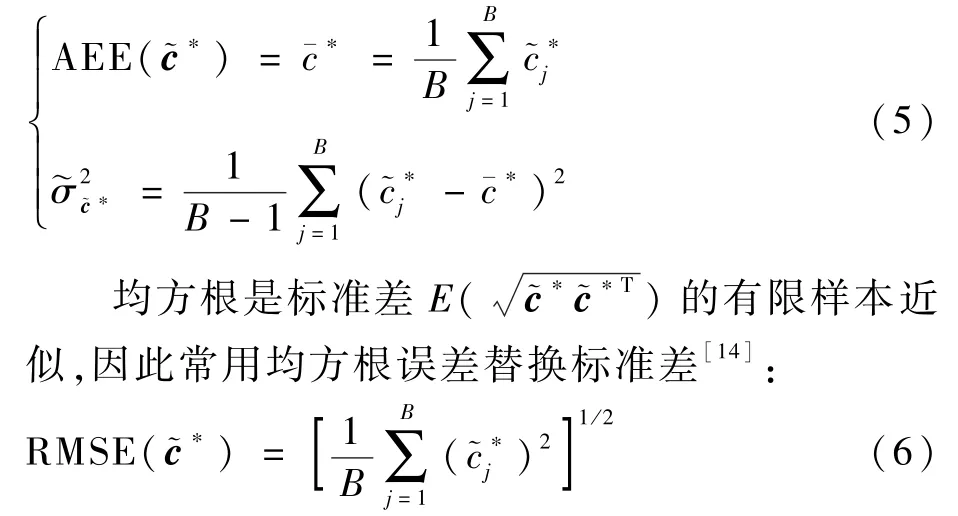
但是实际使用中,有时需关注极小值影响,也就是最高精度能达到多高水平,为此定义调和平均误差评估指标。
2.2 调和平均误差评估指标模型
调和平均误差评估指标的定义为[14]
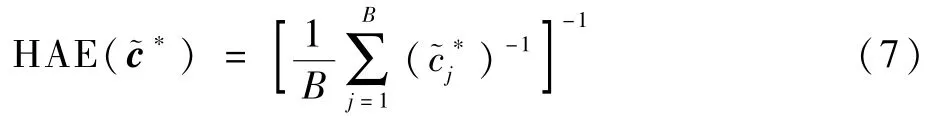
显然,调和平均误差评估指标对误差取倒数后,关注的是极小误差,因此常用于回答命中与否的问题。特别地,当=0时,1/无意义,使得HAE(~c*)无法使用,为此令=0.0001或者换成饱和函数,如Tanh函数、Softplus函数等。
在工程实际中,为了快速得到评估结果,并且遵从原始样本的信息,通常采用误差中位数和误差众数来衡量系统的命中精度。
2.3 误差中位数和误差众数评估指标模型
误差中位数是指在样本~c*中利用中间序号对应的样本点作为系统的命中精度,即[14]
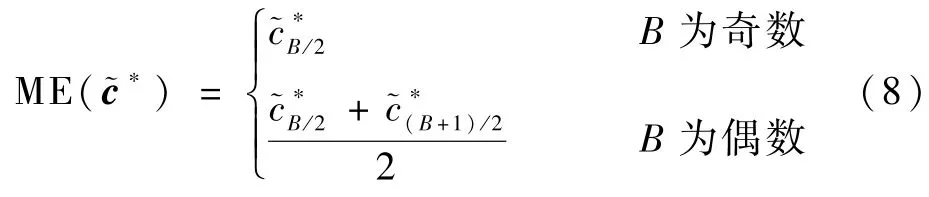
可见,中位数未考虑其他样本点的信息,仅考虑了中间点样本的信息。为了克服该问题,工程实际中通常采用误差众数来衡量系统的精度。而误差众数EMM()是指样本中出现频率最大的值。
进一步,在工程实际中,为了评估系统命中精度的平稳性,定义几何平均误差评估指标。
2.4 几何平均误差评估指标模型
几何平均误差评估指标的定义为[14]
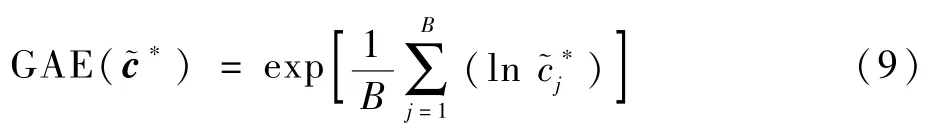
几何平均误差评估指标既不受粗大值影响,也不受极小值影响,因此其能够反映系统命中精度的平稳性。同样的,当=0时,使得GAE()也无法使用,令=0.0001或者换成饱和函数。
2.5 迭代中距误差评估指标模型
为了克服算术平均误差和均方根误差评估指标受大误差的影响,文献[16]又给出了迭代中距误差评估指标,即

下面举例说明迭代中距误差的实施过程。假设获得的误差数据为{1,3,8,9,15},第1次k′=1迭代中距误差为IMRE(~c*)1=(1+15)/2=8;则新的误差数据为{3,8,8,9},第2次k′=2迭代中距误差为IMRE(~c*)2=(3+9)/2=6;同理新的误差数据为{6,8,8},第3次k′=3迭代中距误差为IMRE(~c*)3=(6+8)/2=7;新的误差数据为{7,8},最 终k′=4的 迭 代 中 距 误 差 为IMRE(~c*)4=(7+8)/2=7.5。
3 基于误差谱的高超声速飞行器命中精度高准确度评估
基于误差谱的高超声速飞行器命中精度高准确度评估是指不仅要给出高超声速飞行器命中精度的结果,还要给出高超声速飞行器命中精度评估结果的可信度。
3.1 高超声速飞行器命中精度评估模型
因为定义算术平均误差、均方根误差、调和平均误差、误差中位数、误差众数、几何平均误差和迭代中距误差评估指标在评估高超声速飞行器命中精度时仅能从某一个方面反映系统的性能,所以为了准确、综合和全面地评估高超声速飞行器的命中精度,本文提出误差谱度量(error spectrum,ES)来评估高超声速飞行器的命中精度。
误差谱度量是一个综合性度量[13,17],其包含了很多常用的绝对误差度量,综合考虑了大误差和小误差的影响,因此能够给出一个更加公正的评估结果。下面介绍误差谱度量的定义。
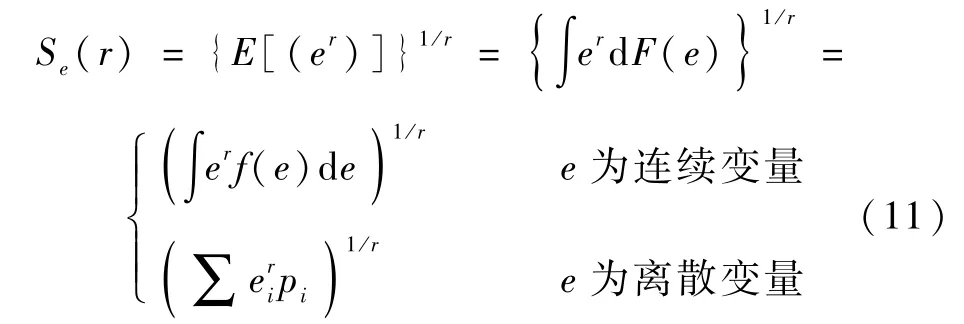
式中:F(e)、f(e)和pi分别表示e的累积分布函数、概率密度函数和分布律。
由式(11)可得,对于给定的e,S(r)是关于r变化的一条曲线,并且误差谱曲线越低,系统的性能越好[17-18]。特别地,当r=-1,0,1,2时,该段误差谱曲线包含了常用的4个绝对误差度量的指标,即RMSE、AEE、GAE和HAE。
3.2 高超声速飞行器命中精度可信度模型
根据高超声速飞行器的特点,给出命中精度的评估结果后,还需给定对该结果的可信度,最终给出高超声速飞行器高准确度的评估结果。下面定义高超声速飞行器命中精度的可信度模型。
一般情况下,可信度评估可分为2种。第1种是将评估结果与真值比较,通过比较评估结果与正值的接近程度,给出该评估结果的可信度。但是,该方法在工程实际中使用比较困难,因为真值一般情况无法获得,通常采用一个与真值比较接近的值作为标准。可见,该方法的难点是寻找一个标准,作为可信度评估的参考。
如图2所示,第2种方法是专家投票法,基于少数服从多数的原理,计算评估结果的可信度。例如,若选择NZJ=10位专家对系统进行打分,其中有6位专家一致认为实测值接近真实值,则该测量结果的一致程度为6/10=0.6。通常情况下,将这种一致程度称为测量结果的可信度。因为第2种方法实现起来比较容易,所以得到了广泛应用[13-14]。下面给出高超声速飞行器命中精度的可信度。
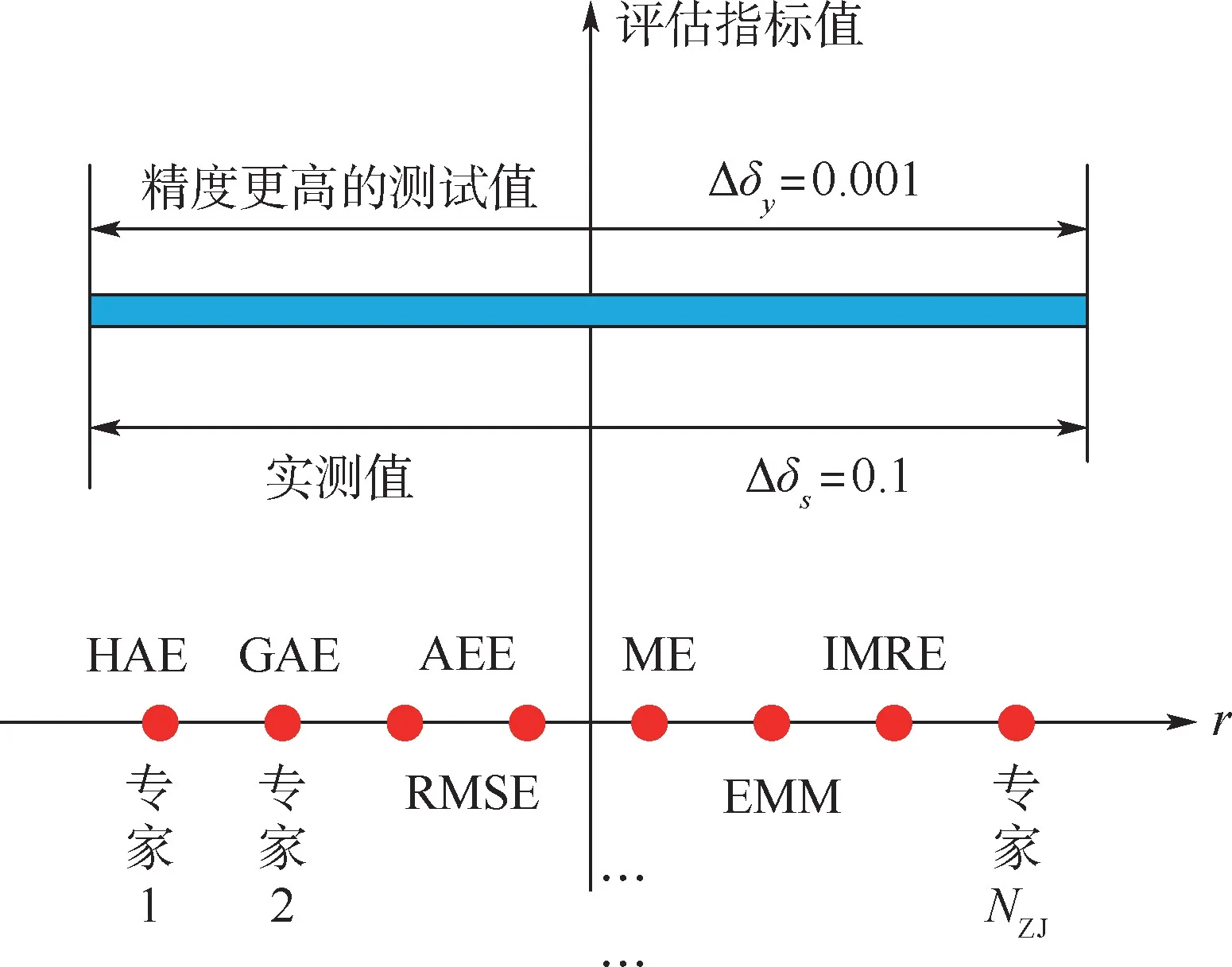
图2 两种可信度评估方法示意图Fig.2 Schematic of two credibility assessment methods
高超声速飞行器命中精度可信度是指利用不同的评估指标,评价相同条件下高超声速飞行器的命中精度时评价结果的一致性程度。
比较两型高超声速飞行器的命中精度,得到2组高超声速飞行器的命中精度的扩容数据~c*1和~c*2,代入本文提出的算术平均误差、均方根误差、调和平均误差、误差中位数、误差众数(EMM)、几何平均误差和迭代中距误差评估指标中得到

可以看出,针对这两型高超声速飞行器的命中精度,利用不同的指标得到不同的评估结果。上述评估结果中,HAE、GAE、ME、EMM和IMRE一致认为系统2的精度要高于系统1,因为系统2的误差小于系统1的误差。只有AEE和RMSE认为系统1的精度要高于系统2。该评估结果的一致程度为Mc=5/7=0.71。因此可得,系统2的精度要高于系统1,该评估结果的可信度为Mc=5/7=0.71。
下面根据3.1节中的命中精度度量指标,给出高超声速飞行器命中精度可信度的计算模型。
3.2.1 建立高超声速飞行器命中精度评估矩阵

式中:N表示N个被评的高超声速飞行器。
3.2.2 建立高超声速飞行器命中精度可信度评估矩阵
基于上述高超声速飞行器命中精度评估矩阵H,运用皮氏接近度原则(Pitman’s closeness measure)建立高超声速飞行器命中精度可信度评估矩阵。
记Mc(j,k;Hi(j,k))为打分矩阵H中的第j列与第k列元素的比较结果,得分的依据为

式中:Hij<Hik表示用第i个评估指标评估时,第j个高超声速飞行器的命中精度优于第k个高超声速飞行器的命中精度,因为H中的元素是误差值;Hij=Hik表示用第i个评估指标评估时,第j个高超声速飞行器的命中精度与第k个高超声速飞行器的命中精度相当。
进一步,可得高超声速飞行器命中精度的可信度为

当R(j,k;H(1,…,7)×N)>0.5时,则系统j的命中精度比系统k的命中精度高,且该评估结果的可信度为R(j,k;H(1,…,7)×N)。
综上所述,根据式(11)和式(16)可得最终的评估结果如下。
命中精度:

可信度:

式中:Se(r)p≻Se(r)q表示第p个高超声速飞行器的命中精度优于第q个高超声速飞行器的命中精度,p,q=1,2,…,N。
特别地,当仅评估一个高超声速飞行器的命中精度时,将期望的高超声速飞行器的命中精度作为参考对象(或为预先设计的高超声速飞行器的命中精度)Se(r)o。
命中精度:

可信度:

认为被评估的高超声速飞行器命中精度满足要求,该结果的可信度为Mc(p,o;H(1,…,7)×N),否则该系统的命中精度不满足要求,而不满足要求的可信度为Mc(o,p;H(1,…,7)×N)。
4 仿真验证
为了验证本文方法的正确性,评估某三型高超声速飞行器命中精度。假设数据服从二维正态分布,分布参数如表1所示。
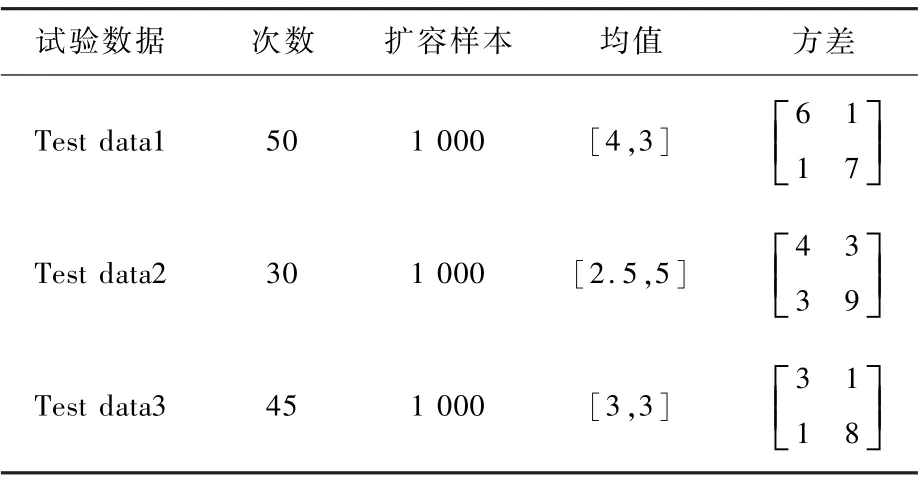
表1 三次试验服从的二维正态分布参数Table1 Two-dimensional normal distribution which parameters of three tests follow
4.1 单次仿真验证
用文献[14]中的扩容方法后得到的数据如图3所示。由式(14)可得到误差数据如图4所示。
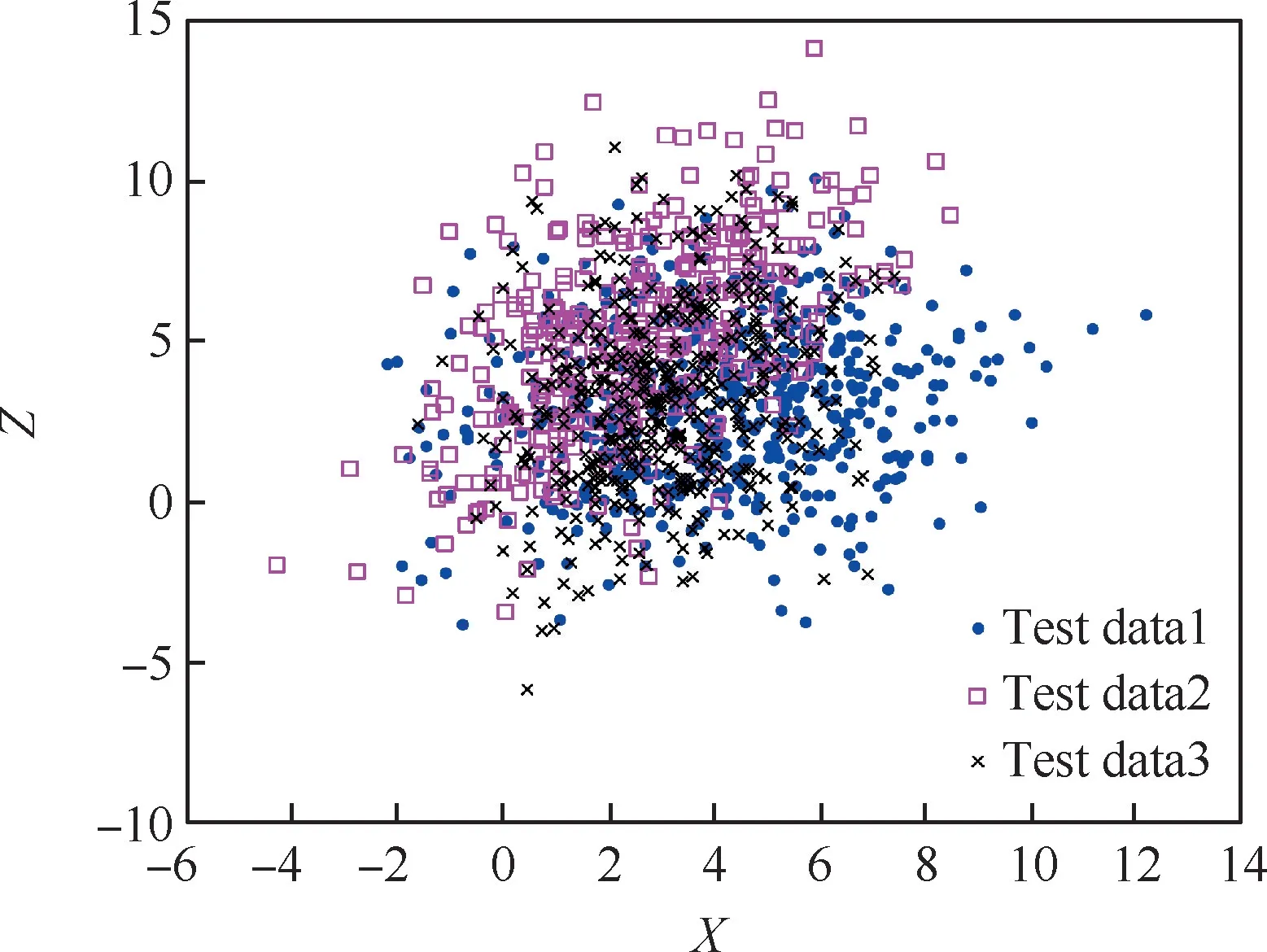
图3 三种试验原始数据Fig.3 Original data of three types of test data
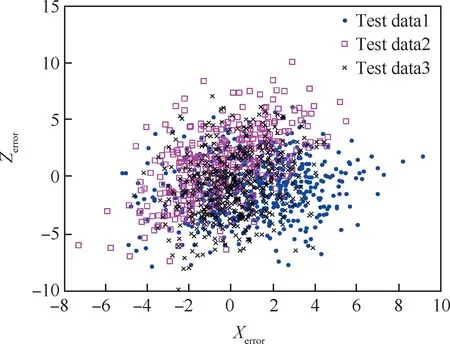
图4 三种试验误差数据Fig.4 Error data of three types of test data
进一步,将上述3组数据代入式(12)可得数据的误差谱曲线,如图5所示。
由图5可得,可以直观看出3组数据对应的高超声速飞行器命中精度的优劣,即
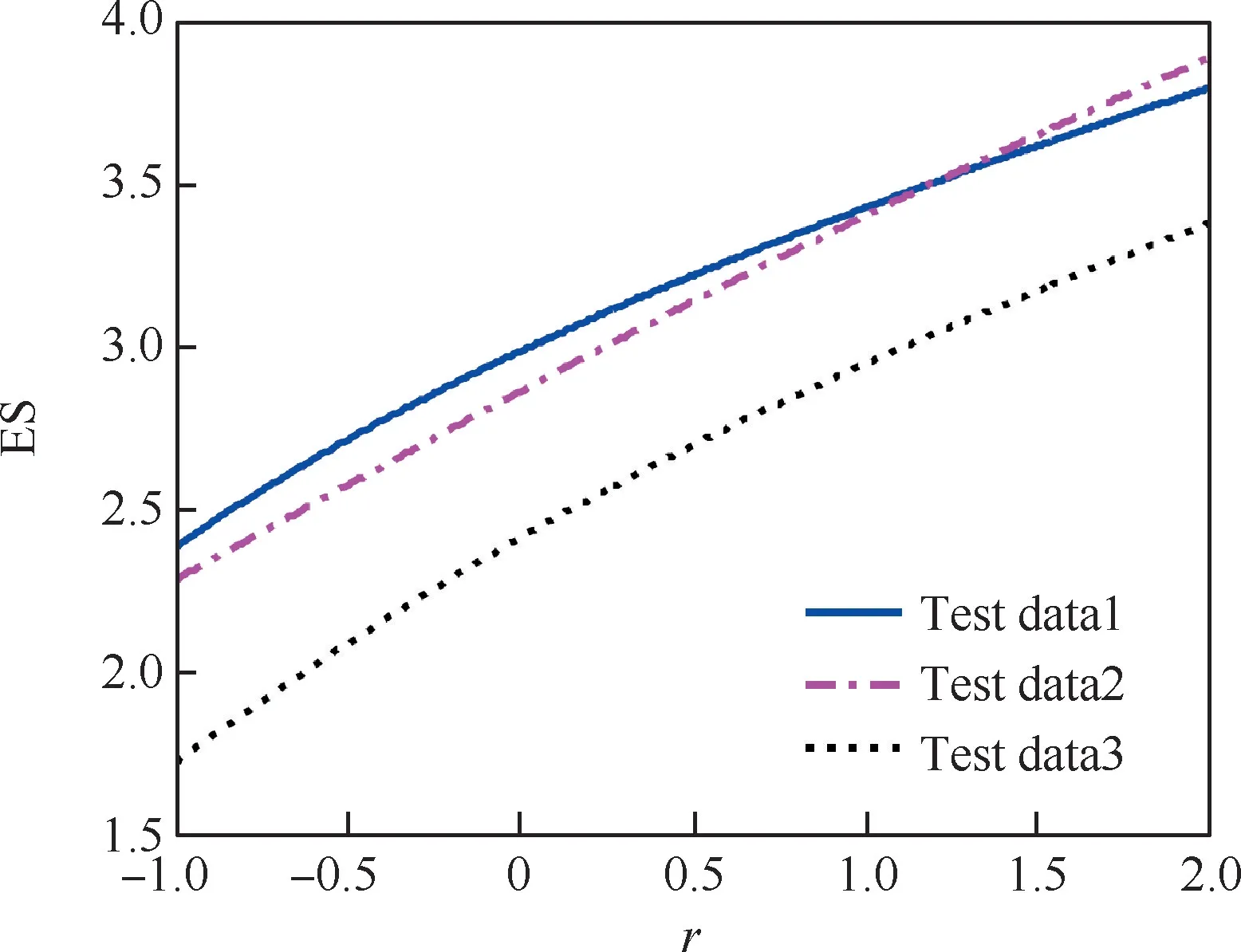
图5 三种试验数据误差谱曲线Fig.5 Error spectrum curves of three types of test data
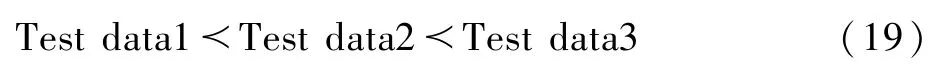
式中:X≺Y表示系统Y的命中精度优于系统X的命中精度。
将数据代入式(13)可得
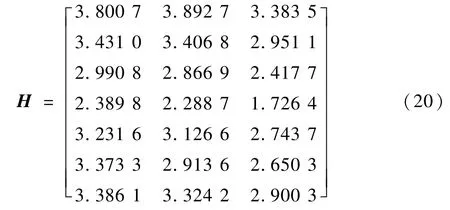
进一步,根据式(16)可得高超声速飞行器命中精度的可信度矩阵为

可见,R(3,1)=1>0.5,则说明系统3的命中精度优于系统1的命中精度,且可信度为R(3,1)=1。又根据误差谱曲线的特征可知,曲线越低,性能越好,显然系统3对应的虚线误差谱曲线低于系统1对应的实线误差谱曲线。结果证明上述可信度评估的正确性。
同理,R(2,1)=0.8571>0.5,则说明系统2的命中精度优于系统1的命中精度,且可信度为R(2,1)=0.8571。对应的误差谱曲线可得,点画线误差谱曲线与实线误差谱曲线有交叉,也进一步说明有“专家认为”系统1的命中精度优于系统2的命中精度。
4.2 多次仿真验证
根据4.1节中的仿真,运用MATLAB软件仿真M=1000次,结果如图6~图8所示。

图6 试验数据1和试验数据3的误差谱曲线Fig.6 Error spectrum curves of Test data1and Test data3
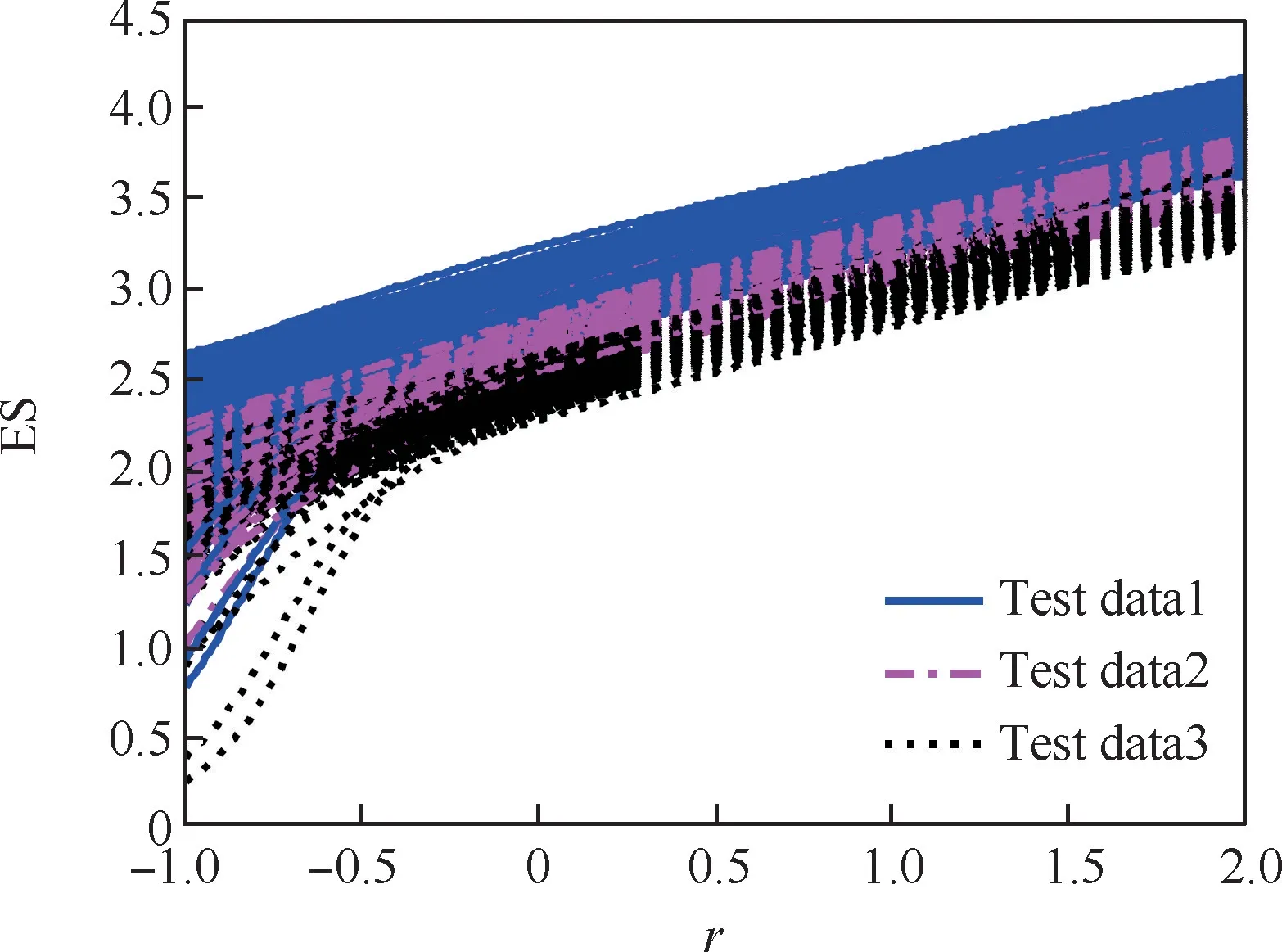
图8 三种试验数据的误差谱曲线Fig.8 Error spectrum curves of three types of test data
进一步得到平均可信度矩阵为

同理,如图6所示,系统3对应的点线误差谱曲线低于系统1对应的实线误差谱曲线,因此,系统3的命中精度优于系统1的命中精度。该结果与单次仿真的结果一致。但是,从图6中可以看出,有少部分结果显示,系统3对应的点线误差谱曲线高于系统1对应的实线误差谱曲线。换句话说,就是系统3的命中精度不总是优于系统1的命中精度,即系统3的命中精度优于系统1的命中精度的可信度不为1。利用本文方法得到该可信度为(3,1)=0.9674,可以准确反映该结果,显然再次证明上述可信度评估的结果是正确的。
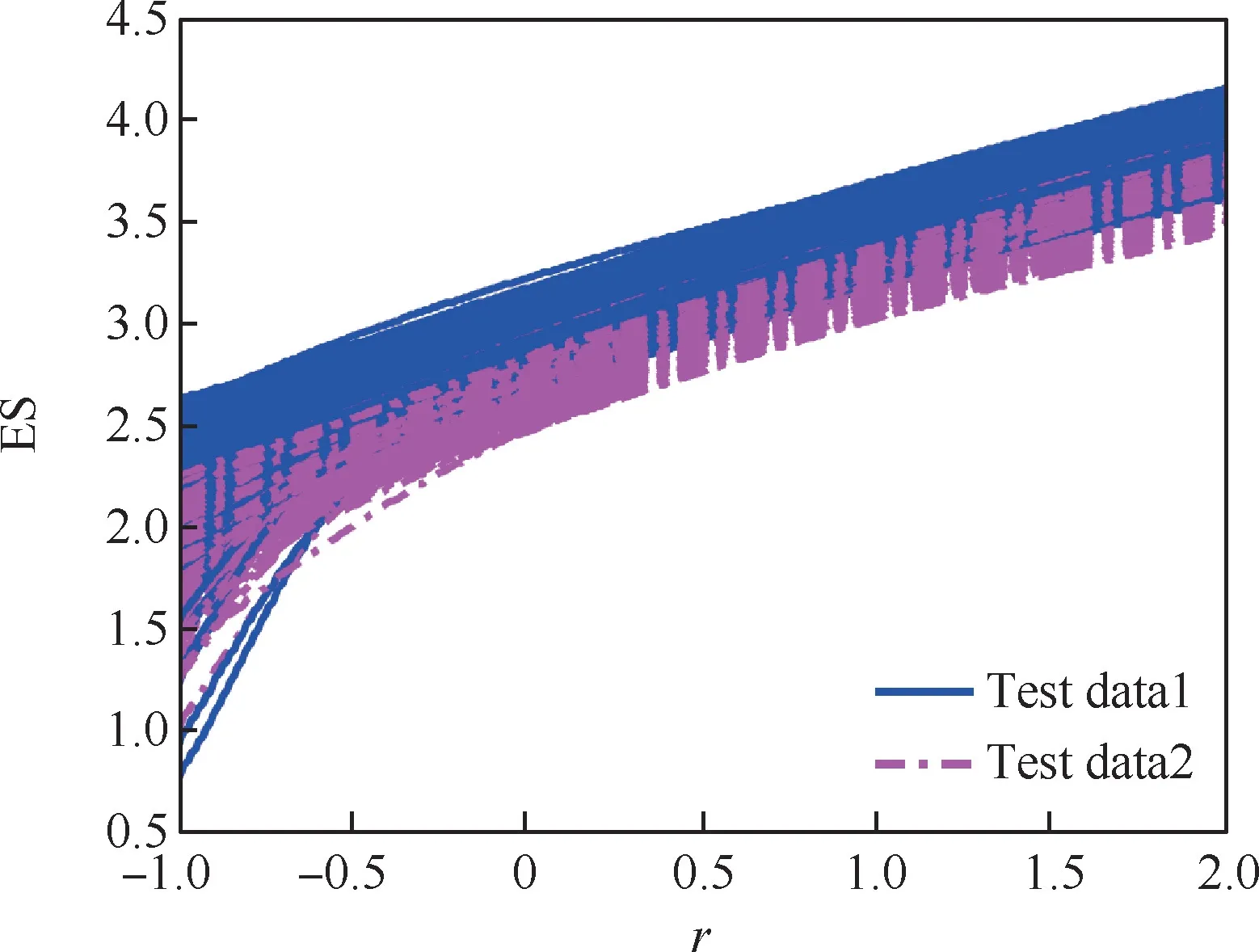
图7 试验数据1和试验数据2的误差谱曲线Fig.7 Error spectrum curves of Test data1and Test data2
进一步由图8可得,在多次仿真的条件下,利用不同的评估指标评估高超声速飞行器的命中精度时,可能得到不一致的评估结果。此时,应该考虑用多种评估指标评估高超声速飞行器的命中精度,给出最终评估结果的一致性,即该评估结果的可信度,这样才能准确地给出高超声速飞行器的命中精度。
综上所述,可得三型高超声速飞行器命中精度评估结果为

5 结 论
本文提出了一种高超声速飞行器命中精度高准确度评估方法,不仅能给出高超声速飞行器命中精度评估结果,还能给出该结果的可信度。
1)建立了算术平均误差、均方根误差、调和平均误差、误差中位数、误差众数、几何平均误差和迭代中距误差的评估模型,从不同的方面反映了系统的命中精度,为后续高超声速飞行器命中精度及其可信度评估提供指标支撑。
2)为了综合反映高超声速飞行器命中精度的性能,提出了用误差谱曲线评估高超声速飞行器的命中精度,克服了单一评估指标仅反映系统一方面性能的缺陷。
3)将上述高超声速飞行器命中精度评估指标定义为可信度评估中的“打分专家”,进而构建高超声速飞行器命中精度评估矩阵,并根据皮氏接近度原则建立高超声速飞行器命中精度可信度评估矩阵,并给出了可信度评估结果。
基于高超声速飞行器命中精度高准确度评估方法还需经过更多的实际应用才能验证该方法的可行性。
