一种基于激光位移测量的机械臂参数标定方法

邵鑫,季力,邹怀武,解杨敏,*

(1.上海大学 机电工程与自动化学院,上海 200444; 2.上海市空间飞行器机构重点实验室,上海 201108)

机器人的定位精度是衡量其性能最重要的指标之一。其重复定位精度主要受关节控制误差的影响,现国内外应用的机器人一般能够达到亚毫米级。但其绝对定位精度一般在毫米级,通常为2～3mm[1],这在很大程度上降低了其在精密作业中的应用效果。研究表明,机器人绝对定位精度的最大影响因素为其运动学参数的误差,其影响约占到系统总误差的65%～95%[2]。机器人的运动学参数标定是解决这一问题的基本方法。其原理为构造及优化某种与运动约束相关的误差函数,以矫正运动学模型中的机器人名义结构参数,使其更接近于真实加工及安装状态。

一般来讲机器人的参数标定按照约束建立的方法可分为三大类[3]:外部直接测量法[4-6]、外约束标定法[7-8]、自约束标定法[9-11]。外部直接测量法通常利用高精度仪器对机器人末端位置进行三维测量,并以此作为标定约束,这类方法数学建模过程简单,但通常需要昂贵的测量仪器和实施环境支持;外约束标定法利用安装于机器人末端的传感器在不同的空间位置测量与外部参照物的相对位姿关系,从而形成空间约束,这类方法使用的测量仪器相对简单廉价,但需要设计合理的外部参照物;自约束标定法则是通过构建封闭运动链以利用自身的运动学建立几何约束,虽其误差函数构建不依赖参照物,但通常需要外部参考建立封闭运动链,且其数学模型相对复杂。

本文的工作属于外约束标定的范畴。外约束标定通常具有易于计算和实践的优势,已获得广泛的应用。在已有的研究中使用最常见的测量装置有视觉传感器[12-13]和接触式传感器[14-15]两大类。接触式传感器操作较为复杂,且存在碰撞和仪器损伤风险,因此在近年的研究中越来越多地使用视觉进行标定[16-17]。视觉测量的优势是操作相对简单,但需要进行传感器自标定,且测量精度易受参照物和环境(如标定板和光照)等因素影响。为此本文提出一种利用末端安装的激光位移计测量与外部参照物相对位置关系的方法,同时具有使用便捷、成本低廉、测量稳定及数据获取简单的特点。

为了合理约束多自由度机械臂空间运动,本文设计了相互近似垂直的3个平面参照物。研究表明,单纯的平面方程不足以对多自由度机器人形成足够的空间约束[18],因此本文提出了平面度与平面夹角相结合的约束构建方式,形成多目标误差函数。相关的标定方法在实验系统上进行了验证,且与基于高精度激光追踪仪的参数标定进行对比实验,并对两者误差进行对比分析,从而对本文方法的参数标定效果进行了全面性的评价。

1 运动学建模

机器人的运动学模型是参数标定的基础。考虑到串联机器人建模的标准化和连续性,本文使用坐标系后置DH参数法[19]建立其运动学模型。机器人基坐标系位于安装基座的中心处,根据DH参数法建立每个连杆坐标系,再用齐次变换矩阵描述相邻连杆之间的空间关系[20]。六自由度机械臂DH模型坐标系如图1所示,机械臂DH参数的初始名义值如表1所示。

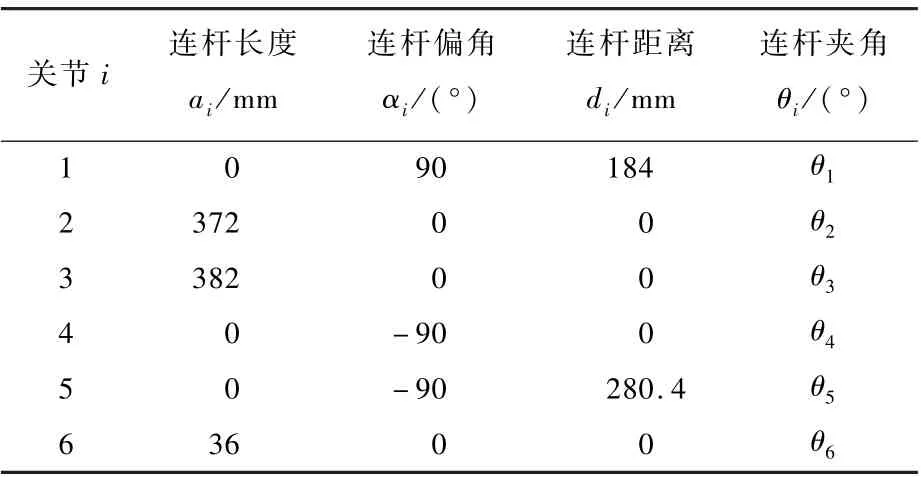
表1 DH参数Table1 DH parameters

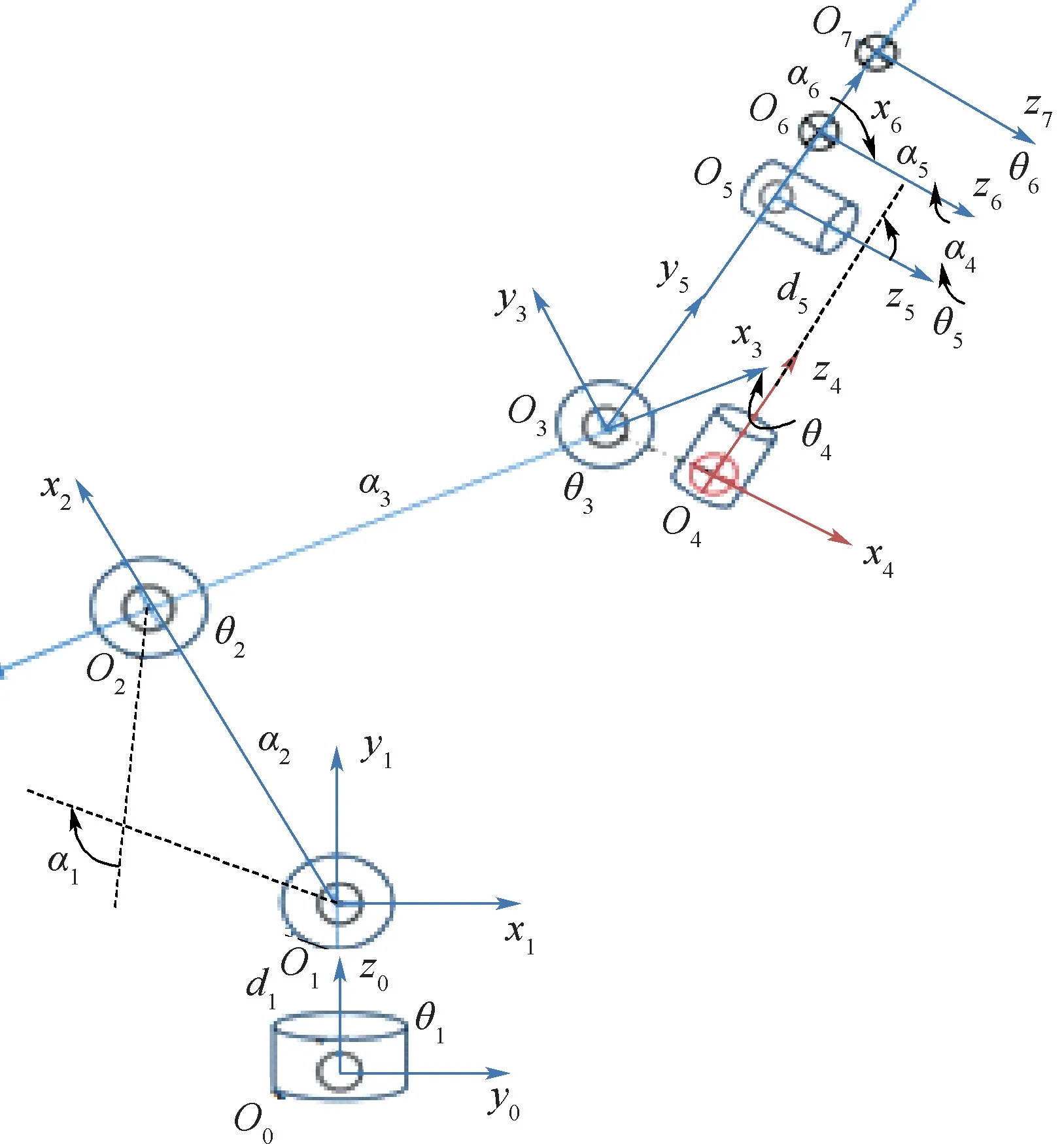
图1 机械臂DH模型坐标系Fig.1 DH model coordinate system of manipulators

由连杆坐标系{i}和相应的连杆参数建立机械臂运动学方程,得到末端执行器相对于基坐标

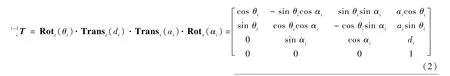
系{B}的齐次变换矩阵:

其中相邻关节对应的位姿变换矩阵可以写为

式中:Rotz(θi)和Rotx(αi)分别为绕z轴和x轴旋转θi和αi对应的旋转矩阵;Transz(di)和Transx(ai)分别为在zi和xi方向上平移di和ai对应的平移矩阵。

由于编码器回零误差、加工装配误差等因素,每个连杆的4个DH参数都存在误差,记为Δθi、Δai、Δαi、Δdi,则六自由度机械臂共有24个误差参数。为建立机器人末端误差与各误差参数之间的定量关系模型,修正DH参数列表如表2所示。

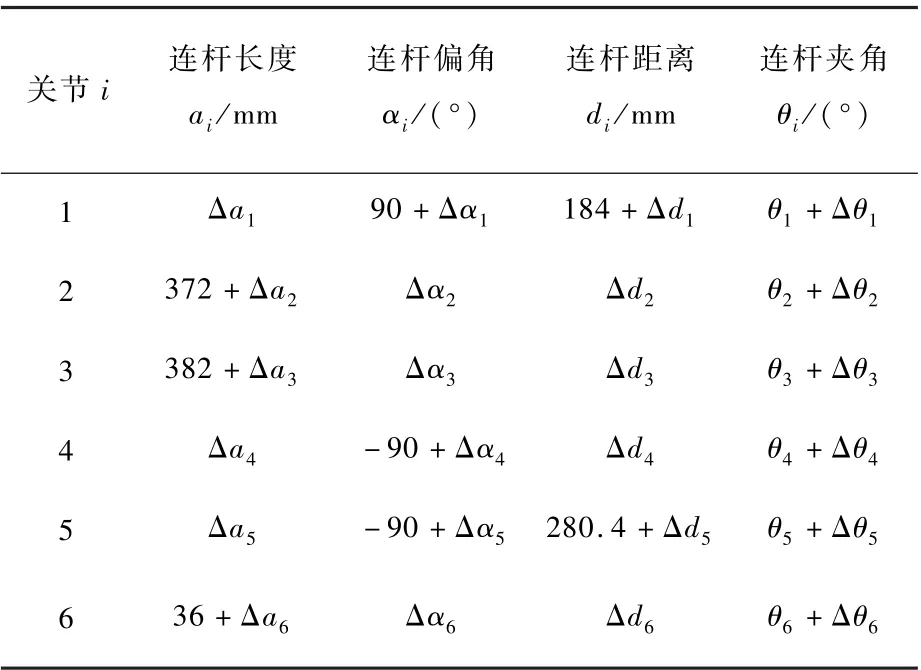
表2 DH误差参数Table2 DH parameters with kinematic errors

故包含机器人误差参数后的变换矩阵可表示为

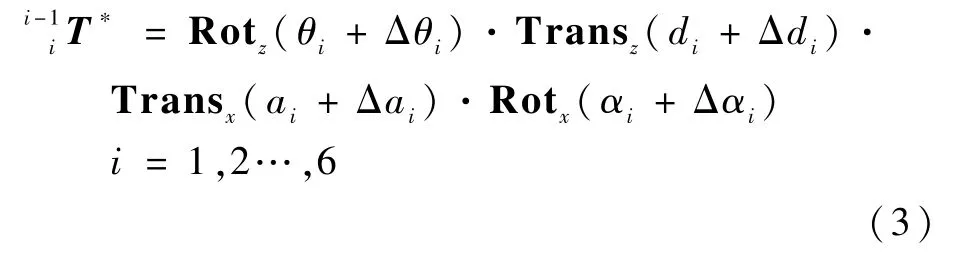
2 参数标定方法

2.1 标定原理

传统的机器人参数标定通常需要借助激光跟踪仪、三坐标测量仪等昂贵且操作复杂的工业级设备完成。本文提出了一种创新性的简易标定方法,利用价格低廉且操作简易的激光位移传感器对立方体标定物外部信息进行间接测量,利用多个测量点进行多平面拟合和多平面角度约束,通过已建立的参数误差模型优化求解关节参数误差。

其实验方案如图2所示。激光位移传感器安装于机械臂末端,机械臂操作空间放置两两垂直的立方标定板。激光位移传感器发射出激光束照射在标定板上,通过变换机械臂位姿,采集3块标定板平面上多点测量数据。

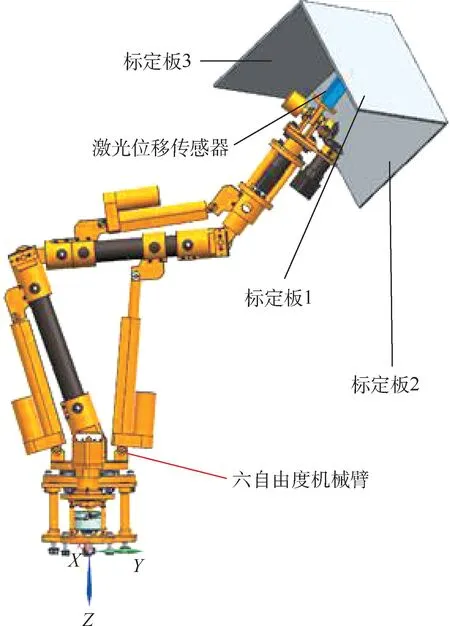
图2 实验方案Fig.2 Experimental scheme

具体测量方案原理如图3所示,激光位移传感器的末端参考点到标定板平面测量点之间的距离用L描述,即为激光位移传感器读数。机器人末端坐标系为Ofxfyfzf,机械臂基坐标系至末端坐标系的位姿变换矩阵为,激光位移传感器末端参考点在Ofxfyfzf下坐标向量为p(x0,y0,z0),单位方向向量为n(nx,ny,nz)。

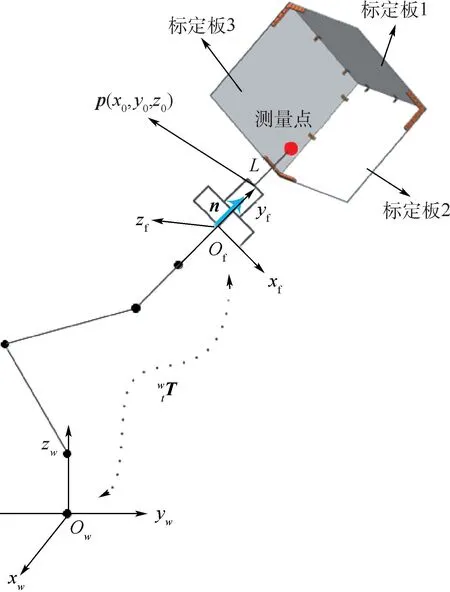
图3 参数标定原理Fig.3 Schematic diagram of parameter calibration

根据激光位移传感器的读数,可以得到3个平面上的测量点相对于激光位移传感器坐标系的位置信息。通过最小化测量点在机械臂基坐标系下3个平面约束和3个平面之间角度约束的误差,可求得机器人DH优化参数。

2.2 标定方法

由图3可知,标定板上的测量点在末端坐标系Ofxfyfzf下的坐标q可描述为

式中:q=(x,y,z)T,则根据机器人末端坐标系与基坐标系之间的齐次变换关系可得

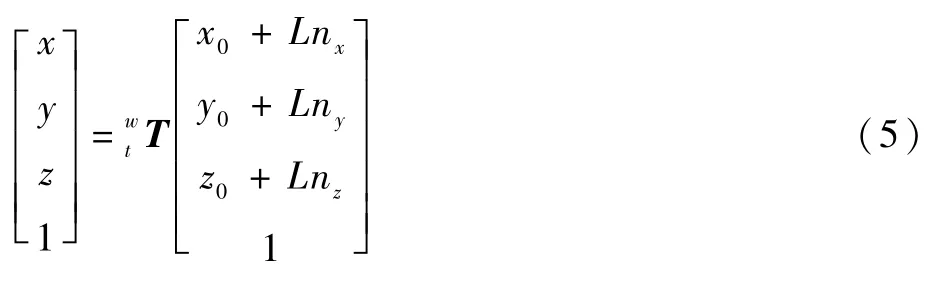
由于在实际的测量过程当中,激光位移传感器实际安装也存在误差,即L与n值并不完全准确,为此定义实际安装参数为L+ΔL和n+Δn。综合考虑表2中24个DH误差参数及ΔL、Δn,系统需要修正的总误差参数个数为28。实际测量点q*的齐次坐标可表示为

式中:ki、bi、ci为平面方程系数。

对于3个平面的Ni个点分别采用最小二乘法进行平面方程拟合,即优化平面方程系数使式(8)中S为最小:

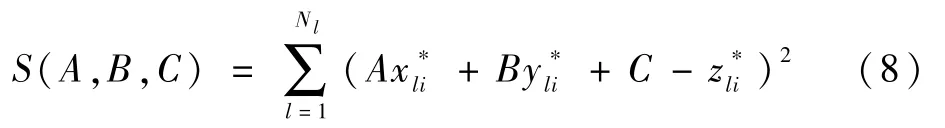
记所得最优系数为A*、B*、C*,则可得式(7)中的平面方程系数为

计算测量点到拟合平面误差为

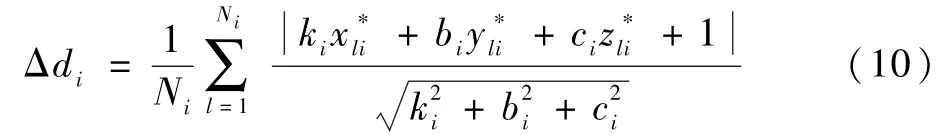
为了保证平面拟合度准确性标定点平面约束给出的误差可定义为

另外,3个拟合平面两两之间的夹角余弦值为

同时考虑标定板平面及标定板间角度约束,建立关于激光位移传感器参数标定的误差函数,如式(14)所示,其变量包括24个DH误差参数及4个激光位移器安装误差参数。

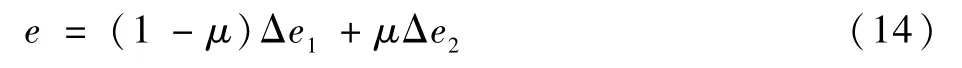
式中:μ为平面和角度影响因素的权重参数;误差e为标定参数的非线性函数,采用能够解决对多约束和多变量结合的非线性问题的全局最优解求解的算法OQNLP[21]进行数值优化并调整最优值,即可得到参数标定结果。

3 标定实验及结果分析

3.1 基于激光位移传感器的标定实验

标定实验场景如图4所示,标定实验系统主要由六自由度机械臂、基恩士LK-H080型号激光位移传感器和标定板组成。该型号激光传感器测量量程为62～98mm,绝对定位精度为0.01mm,重复定位精度可达0.3μm。

图4 激光位移传感器标定实验场景Fig.4 Experimental scene of laser displacement sensor calibration

为确定其安装夹角,利用了光学动作捕捉系统对3块标定板上放置的反光标志点进行三维空间精确捕捉,如图5所示。该系统镜头像素为400万,三维定位精度为±0.1mm。通过拟合每个平面求出标定板间夹角测量值为89.94°,为89.97°,β为90.2°。已知3块标定板平面加工精度为0.1mm。则根据当前标定板的尺寸其角度误差为0.15°。

图5 标定板夹角求解实验场景Fig.5 Experimental scene of calibration plate angle solution

基于激光位移传感器标定实验流程主要如下:

1)将激光位移传感器固定在机械臂末端,将标定板固定于末端运动范围内并保证其平面位置处于激光位移传感器测量量程内。

2)开启激光位移传感器,将激光点照射于标定板1上,记录激光位移传感器读数值Li和机械臂两关节连杆夹角值θi。调整机械臂位姿,记录标定板1不同位置的测量值,尽量使测量激光点在标定板上均匀分布。对标定板2与3重复此步骤。

3)将数据值导入标定误差模型中,利用非线性优化算法最小化目标函数式(14),求解误差参数最优值。

3.2 基于激光跟踪仪的对照标定实验

作为对比验证,本文进行了激光跟踪仪的参数标定实验。实验中使用的设备为美国API公司生产的T3型激光跟踪仪,激光跟踪距离为0～60m,静态测量精度为5μm/m,动态测量精度为110μm/m。使用激光跟踪仪可测得机械臂末端相对于基坐标系{B}的三维坐标,详细过程请参照文献[22]。建立目标函数F为末端三维坐标的计算值与测量值误差和,如式(15)所示,其变量为24个DH误差参数。同样利用非线性数值优化得出使目标函数模型误差最小的DH误差参数,即可得到标定结果。

式中:xi、yi、zi为第i个点的计算坐标;x′i、y′i、z′i为其测量坐标;Mi为测量总点数。

基于激光跟踪仪的机器人参数标定实验场景如图6所示。标定实验流程主要如下:

图6 激光跟踪仪标定实验场景Fig.6 Experimental scene of laser tracker calibration

1)建立机器人基座坐标系,将激光跟踪仪测量坐标系更改为机器人坐标系。

2)转动机器人各关节,记录每个时刻的机械臂两关节连杆夹角值θi,并记录每个时刻激光跟踪仪读数x′i、z′i。

3)将数据值导入标定误差模型中,利用非线性优化算法最小化目标函数求解参数标定最优值。

3.3 实验结果

完全未校核的机器人其名义参数值常大大偏离实际值,因此,通常需要对其进行多次迭代以减少初始偏差对标定优化精度的影响[23]。在本文实验工作中,对标定过程进行了二次迭代。本节主要讨论后一次的精准校正过程和结果。

由2.2节可知,基于激光位移传感器的参数标定实验,评估目标函数误差e求解精度的指标有2个:①激光位移传感器测量点到拟合平面的平均距离误差Δe1;②拟合所得3个平面与实际标定板平面平均角度误差Δe2。权重μ取值一定程度上影响参数优化精度,在不同的μ值下,优化后平面误差及角度误差如表3所示。μ值越小,越倾向于优化角度误差。优选结果应考虑实验条件下作为合理的误差分配参考。如3.1节所述,本实验条件标定板平面度误差为0.1mm,角度测量误差为0.15°。据此应选取μ为0.07时的标定结果,得到e1=1.08mm,e2=0.67°,分别为标定物自身误差的10倍和4.5倍,为有效标定误差。相应的DH参数标定结果如表4所示。

表3 权重μ取值Table3 Values of weight μ

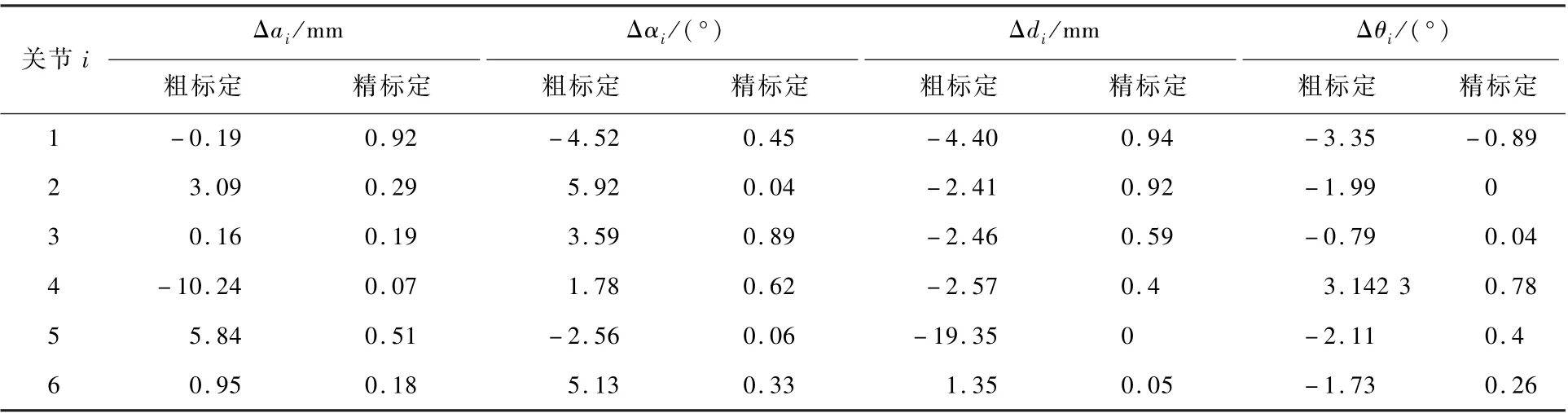
表4 DH参数变化值Table4 Values of DH parameter change

绘制相应的拟合平面,如图7所示,红点为根据优化结果进行DH参数补偿后的激光位移传感器测量点。可以看出,标定补偿后的三维点基本位于标定平面上,且拟合所得3个平面基本两两垂直,符合实验预期。

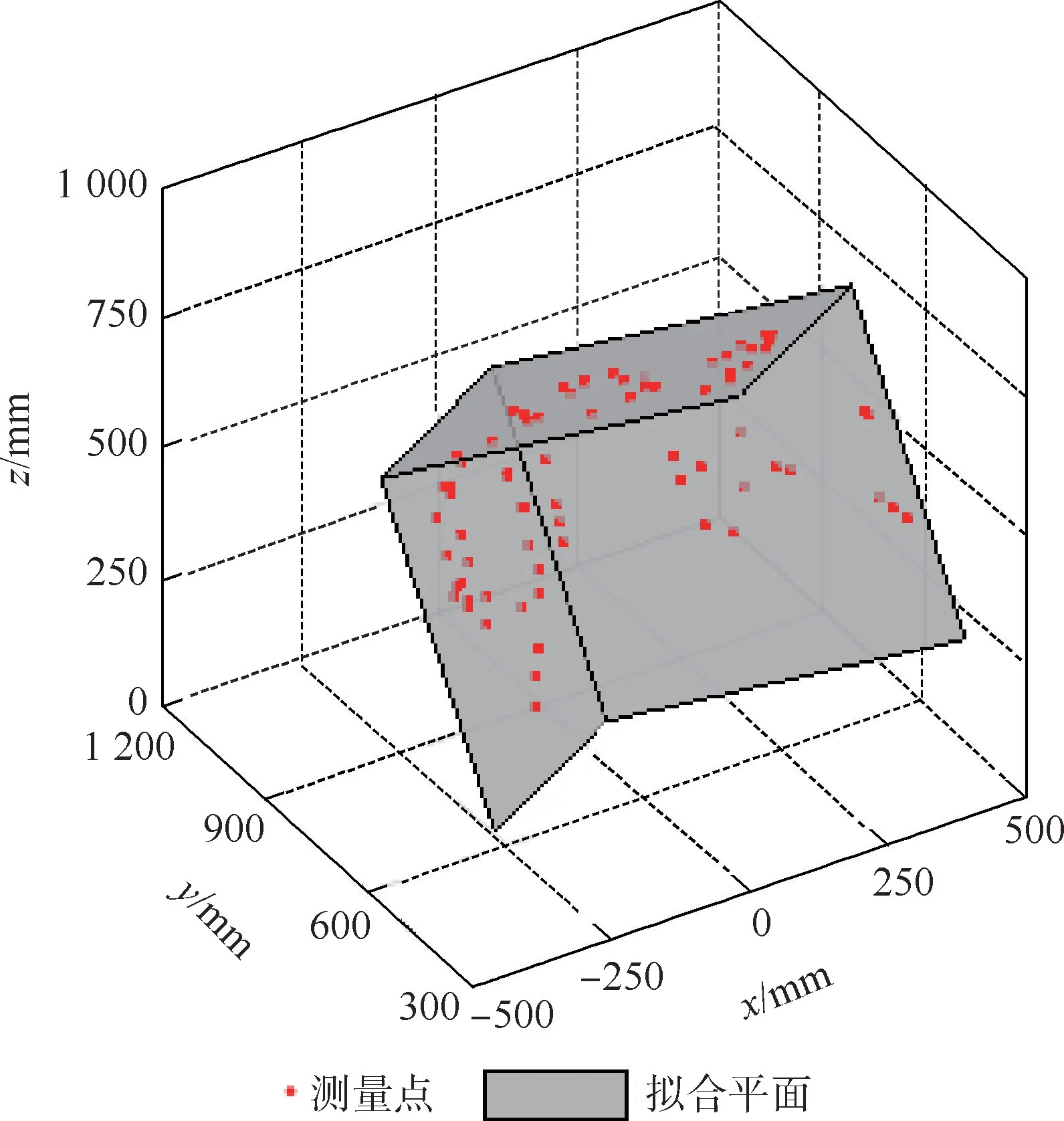
图7 拟合平面结果Fig.7 Graph of fitted plane

基于激光跟踪仪的参数标定对照实验结果如图8所示。使用经过标定的参数后,末端点三维位置基本与跟踪仪测量量吻合,其平均误差为1.01mm。

图8 基于跟踪仪标定后计算坐标和测量坐标对比Fig.8 Comparison of calculated coordinates and measurement coordinates after tracker-based calibration

3.4 误差分析与讨论

本文从2个方面对标定误差进行讨论:①基于激光位移传感器的标定与激光跟踪仪标定精度的比较;②基于激光位移传感器的标定误差与系统重复定位精度的比较。

激光位移传感器与激光跟踪仪在各自53组标定实验数据中的距离误差分布情况如图9所示,其误差数据对比如表5所示。从图9和表5可知,使用激光跟踪仪平均误差为1.01mm,标定后定位误差减小了72.48%;激光位移传感器平均误差为1.08mm,标定后误差减小了71.72%。两者达到了相似的标定结果。若需进一步提升使用激光位移传感器的标定精度,可提高标定板的加工平面度与平面夹角测量精度以增加标准参照物的尺寸精度。

图9 标定误差对比Fig.9 Comparison of calibration errors

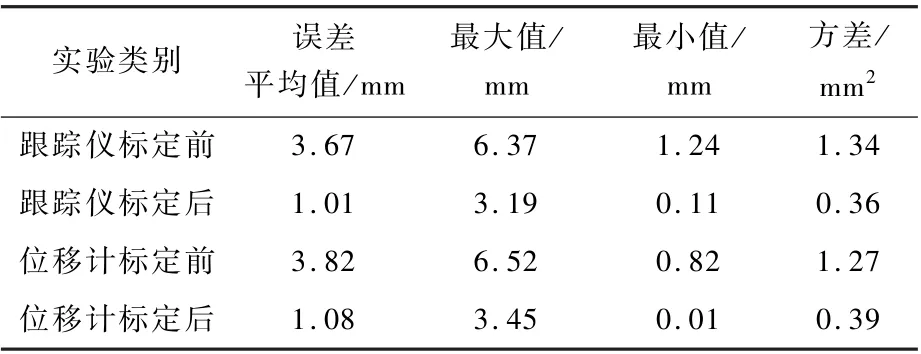
表5 标定实验误差值对比Table5 Comparison of error values of calibration experiment

另外,为了衡量最终标定误差范围相对于实验系统自身精度的合理性,对作为实验对象的六自由度机械臂系统的重复定位误差进行了测量,得到平均重复定位误差为0.74mm。机器人最终标定误差主要由其固有重复定位误差和标定后残余的运动学参数误差两部分组成。由表5标定结果可知,由残余参数误差所致的定位误差仅占系统绝对定位总误差的31.5%,为系统重复定位误差的50%。

4 结 论

本文针对传统机械臂参数标定方法,设备昂贵、技术实现成本高的问题,设计了一种低成本、易操作的利用机械臂末端激光位移计作为测量手段的机械臂参数标定方法。通过实验验证,得到如下结论:

1)设计了立方体面作为外参标定物,利用非接触式激光测量手段,相对接触式测量更为便捷安全,相对视觉测量更为稳定简易。

2)通过构建立方体平面约束及平面间角度约束设计误差函数,利用非线性优化算法最小化目标函数求解可求得误差参数最优值。

3)实验结果表明,本文提出的方法能够达到与使用昂贵的激光跟踪仪相比拟的标定精度,达到良好的标定效果。