旋转抛物-锥形蚀坑模型及其应用
2022-11-30刘德俊田干金国锋杨正伟任碧云魏花丽
刘德俊,田干,*,金国锋,杨正伟,任碧云,魏花丽
(1.火箭军工程大学 导弹工程学院,西安 710025; 2.西安航天复合材料研究所,西安 710025)
火箭推进剂贮箱采用高强度铝合金材料,海底管道、陆地长输管道及压力容器采用不锈钢或低合金钢等材料。在推进剂、海水等输送介质或盛装介质腐蚀作用下,这些金属材料表面极易发生点蚀。由点蚀导致的应力集中会引起裂纹的萌生、扩展等断裂失效问题,从而降低设备的使用寿命,因此,关于蚀坑及其表征模型强度问题的研究一直广受学者关注[1-7]。
为了准确表征蚀坑产生的影响,1954年,Eubanks[8]采用半球描述点蚀坑,实现了蚀坑应力集中的近似分析。但是半球模型无法体现蚀坑形状比对应力集中的影响,为此,1978年,Fujita和Sadavasu[9]将半球形模型发展为半椭球模型,为研究蚀坑的影响提供了更为有效的方法。在此基础上,Cerit[10]通过对半椭球蚀坑应力分布的有限元分析,发现随着蚀坑形状比的改变,最大应力出现在蚀坑底部或坑口下侧位置,拟合出蚀坑与应力集中系数之间的经验公式,并将该成果应用于压力容器的强度分析[11-12],为含蚀坑状态下的压力容器安全分析提供了有效途径。类似地,Hou和Song[13]则基于半椭球形蚀坑模型研究了受拉伸载荷下的蚀坑应力分布。结果发现应力集中系数与蚀坑形状比线性相关,但与蚀坑相对深度成非线性关系。2016年,Li[14]采用半椭球形模型探究了主、次蚀坑的宽度、深度和距离等因素对金属结构强度的影响,结果发现蚀坑的萌生会导致应力集中系数发生乘数效应,使结构的剩余强度大幅度地降低;2019年,Liu等[15]讨论了蚀坑与材料内部孔洞对应力集中的影响,提出了可表征蚀坑形状参数、缺陷距离比等因素的应力集中系数经验公式,丰富了蚀坑模型的研究范围。
但是在工程实际中,蚀坑的几何形状十分复杂,半椭球模型与真实的蚀坑具有非常大的差别。文献[16-18]也认为半椭球形蚀坑演化出的半椭圆裂纹会极大地高估蚀坑引起的应力奇异性,从而会高估结构的剩余强度,造成不必要的资源浪费。为此,Turnbull等[19]在试验观察的基础上提出了更能反映蚀坑真实形貌的U形蚀坑模型,其应力集中现象比半椭球蚀坑更为突出。在此基础上,张川和姚卫星[20]利用U形蚀坑模型研究了危险蚀坑的应力状态,并给定了危险蚀坑的判别准则。文献[21]认为具有尖深边缘且能反映蚀坑底部形貌的蚀坑模型能够准确地表征蚀坑造成的应力集中问题,但是并未建立相应的模型。因此,本文为了准确地表征点蚀坑形貌,描述点蚀产生的应力集中效应,基于蚀坑张开角的重新定义,提出了旋转抛物-锥形蚀坑模型,有效地反映出不同形状比的蚀坑形貌。同时,与半椭球形蚀坑模型进行了有限元对比分析,得到了不同形状比下的蚀坑应力分布规律。最后,采用扫描电镜(scanning electron microscope,SEM)观察拉伸破坏试验件的蚀坑截面,验证了模型的正确性。
1 旋转抛物-锥形蚀坑模型建立
腐蚀环境下,结构表面蚀坑形貌不尽相同。面积、深度、长度等形状特征突出的蚀坑不但影响结构整体强度,还能导致裂纹萌生致使材料断裂破坏。如图1所示,暴露于腐蚀介质中的结构蚀坑形貌,通过观察呈现2种典型情形[20]:图1(a)为浅平蚀坑,特点是坑底狭长,材料表面衔接处应力相对集中;图1(b)为尖深蚀坑,特点是坑底狭窄,应力集中区域多聚集在坑底,且比浅平蚀坑更具破坏性。

图1 典型蚀坑图Fig.1 Typical corrosion pit patterns
在蚀坑形貌观察中,坑底的轮廓可近似简化为光滑过渡。因此,坑底附近区域截面可通过控制曲率半径r的大小来确定蚀坑坑底尖锐的程度。基于上述假设,提出了描述尖深蚀坑及浅平蚀坑的旋转抛物-锥形蚀坑模型。
1.1 尖深蚀坑截面
对于尖深蚀坑,坑底曲率半径r较小且小于蚀坑深度,因此,在蚀坑轮廓线底部做以r为半径的曲率圆。该圆作为旋转抛物-锥形模型的基础起到确定坑底位置的作用。
如图2所示,蚀坑截面轮廓线为GDICH。以坑底I为原点,x、y轴如图2所示,作以O为圆心、r为坑底曲率半径的曲率圆,由于旋转抛物体母线的系数与曲率半径相关,因此过I点做抛物线L,图2中m为蚀坑半长,h为蚀坑深度。
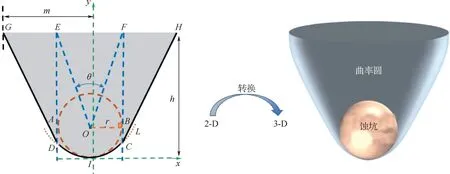
图2 尖深蚀坑示意图Fig.2 Sharp-deep corrosion pit
设抛物线L方程为

式中:p为旋转物体母线系数。
因为I为抛物线顶点,则

过曲率圆分别作平行于y轴且与圆分别相切于点A、B的直线AE和BF,与抛物线L交于点D(r,r/2)和C(r,r/2),定义∠EOF为蚀坑张开角,分别将G、D和C、H线形连接,从而形成尖深蚀坑轮廓线。
根据直线解析式及GD、CH坐标得到解析式:
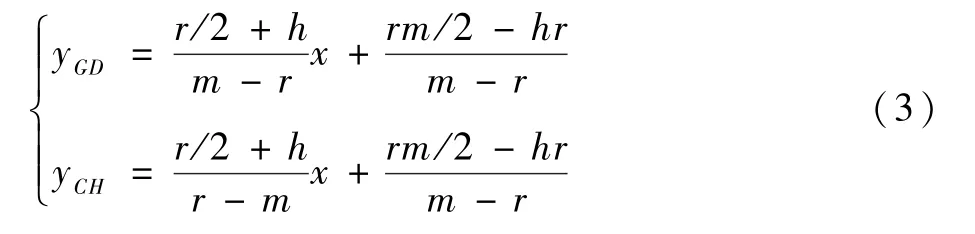
由相应几何关系得到尖深蚀坑张开角θ与坑底曲率半径和蚀坑深度关系:

1.2 浅平蚀坑截面
对于浅平蚀坑,由于坑底曲率半径r较大且常大于坑深h,如图3所示,因此,浅平蚀坑轮廓线的构造与尖深蚀坑轮廓线构造方法有所不同。
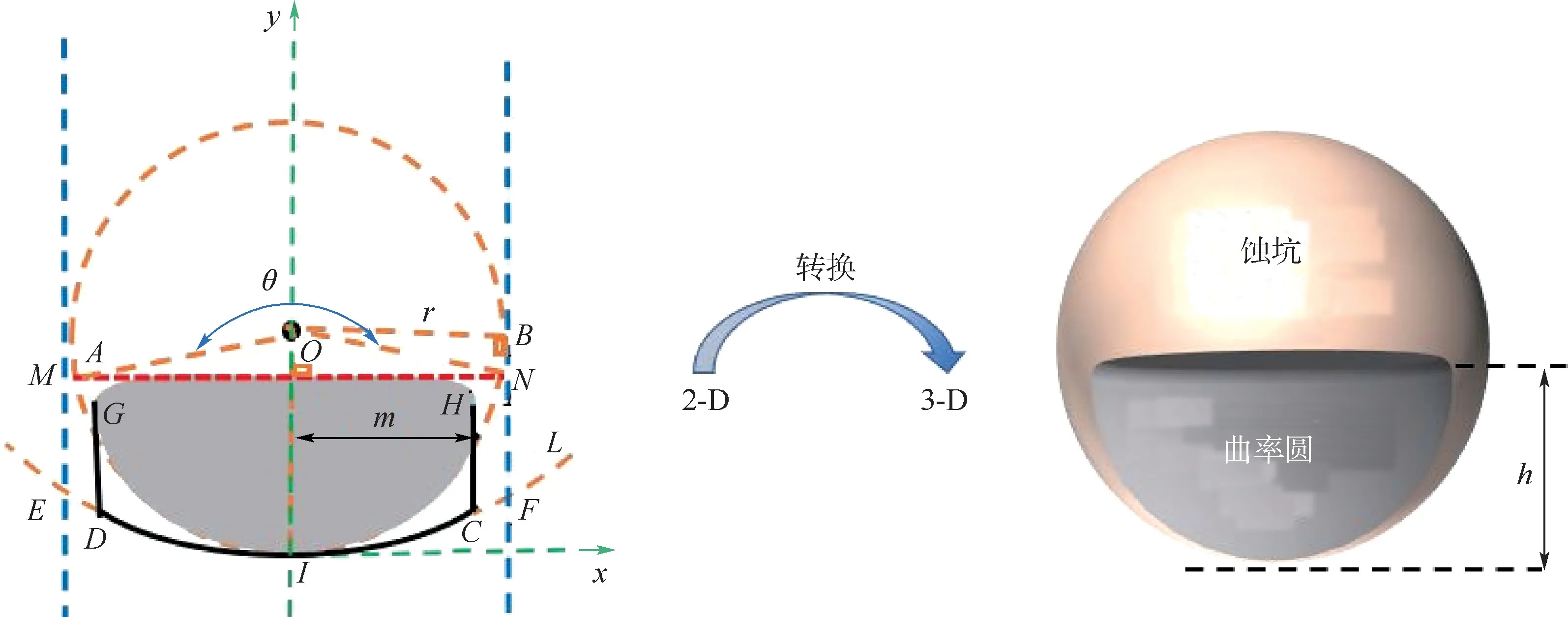
图3 浅平蚀坑示意图Fig.3 Shallow-flat corrosion pit
如图3所示,蚀坑截面轮廓为GDICH。参照1.1节,I为原点,作以O为圆心,r为半径的曲率圆,根据式(1)和式(2)做过点I的抛物线L。AE和BF是平行于y轴与圆相切的2条切线,A、B为切点,E、F是与抛物线L的交点;延长蚀坑上边GH与曲率圆相交于M、N,即MN为曲率圆的割线。过G、F作垂线与抛物线L交于D、C,从而形成浅平蚀坑轮廓线。进而得到GD、CH两个垂线方程为

定义圆周角∠EOF(钝角)为蚀坑张开角θ,由几何关系得到浅平蚀坑张开角θ与坑底曲率半径和蚀坑深度的关系:
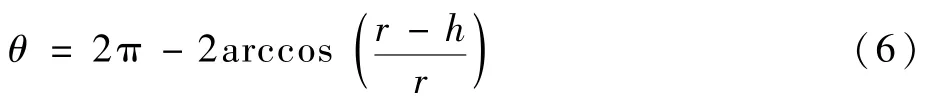
通过对尖深蚀坑与浅平蚀坑建模分析,能够得到张开角是关于蚀坑深度及蚀坑底部曲率半径的函数。当r<h时,蚀坑为尖深蚀坑,此时张开角在(0,90°)内;当r≥h时,蚀坑为浅平蚀坑,此时张开角范围为[90°,180°)。为简化蚀坑模型表达,定义形状比λ=m/h,坑底平整度γ=r/h,得到抛物线-线型蚀坑模型如下:
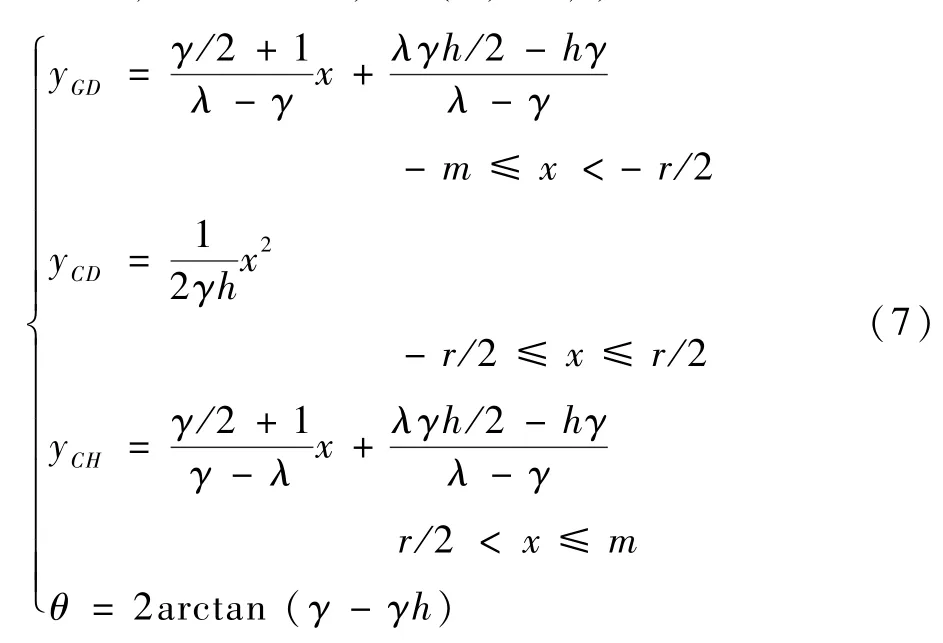
1)尖深蚀坑,θ∈(0,90°),r<h

2)浅平蚀坑,θ∈[90°,180°),r≥h
1.3 蚀坑截面比较
半椭球形蚀坑是根据蚀坑近似长度及深度简化成椭圆长短径而得到的,该蚀坑模型虽然比较简便,但是其关于应力集中敏感性仍有待商榷。因此,该部分将通过改变形状比λ=m/h、坑底平整度γ=r/h,将不同蚀坑张开角下的旋转抛物-锥形蚀坑与等深等长的半椭球蚀坑截面进行比较,其中h为0.5mm。如图4~图6所示,当蚀坑长度和深度一定,半椭球蚀坑对蚀坑形态的变化不敏感,而旋转抛物-锥形蚀坑则能通过坑底曲率半径的改变调节坑底的尖锐或平整程度,即随着曲率半径的增大,蚀坑可由尖深坑过渡到浅平坑。
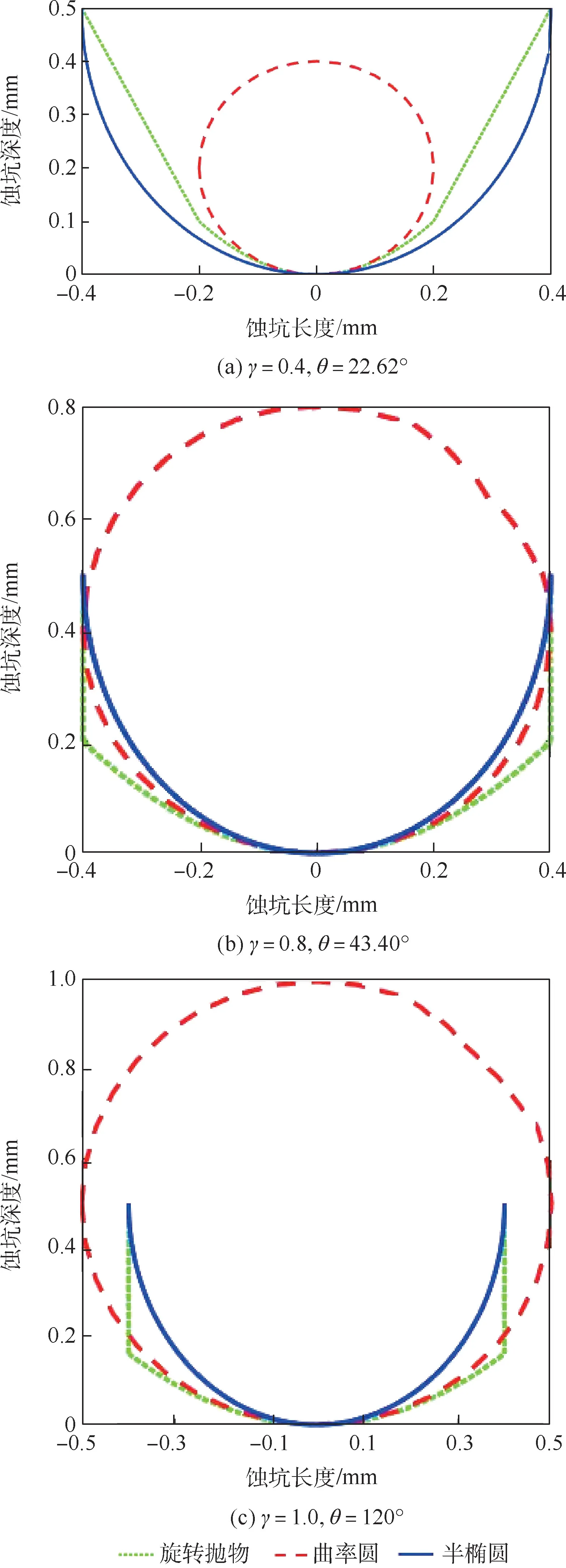
图4 λ=0.8的蚀坑形貌比较Fig.4 Comparison of corrosion pit morphology under λ=0.8
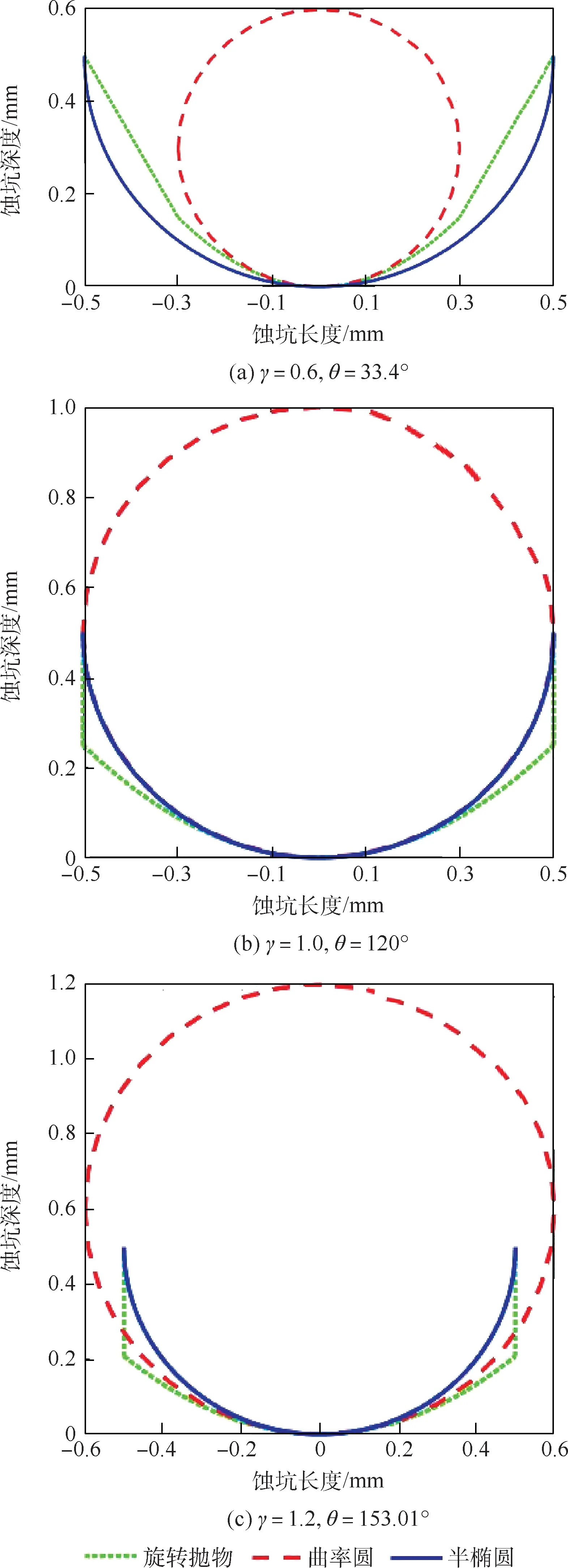
图5 λ=1.0的蚀坑形貌比较Fig.5 Comparison of corrosion pit morphology under λ=1.0

图6 λ=1.2的蚀坑形貌比较Fig.6 Comparison of corrosion pit morphology under λ=1.2
对于θ<90°的尖深蚀坑,半椭球形蚀坑所围成的截面面积大于旋转抛物-锥形蚀坑的截面面积,因此后者更能反映应力集中的现象;而对于θ>90°的浅平蚀坑,旋转抛物-锥形模型截面面积更大,所多出的面积主要集中在蚀坑侧面边缘处,因此旋转抛物-锥形蚀坑从形貌上更能符合该类蚀坑的“浅、平”的特点。综上,与常规的半椭球蚀坑相比,旋转抛物-锥形蚀坑能够在蚀坑深度、长度一定的条件下针对蚀坑尖锐平整程度较为准确的反映蚀坑形貌。
2 三维蚀坑数值分析
2.1 有限元模型建立
分别将相同λ的旋转抛物-锥形及半椭球形蚀坑建立在长为10mm、宽为10mm、高为5mm的长方体平板上,材料为铝合金,弹性模量为70GPa,泊松比0.28,屈服应力290MPa。如图7所示,平板一端固定,另一端施加100MPa的均匀压力,进而得到不同λ的蚀坑周边应力大小及分布情况;网格划分中,蚀坑周围采用10节点的Solid187四面体单元,蚀坑其余部分通过20节点Solid186六面体单元划分,采用局部控制的方式对蚀坑周边进行局部加密。

图7 模型加载条件与蚀坑网格模型Fig.7 Boundary condition and mesh model
为证实数值建模的准确性,文献[13]已对有限元法在不同蚀坑应力分析中得到了数值上的应用,并将蚀坑数值应力求解与理论求解进行了比对。因为弹性力学中带圆孔平板的理论应力分布已知,所以由圆孔中心处向外不同位置处的Mises应力能够被估计。
表1比较的是平板上半径b为0.4mm的孔,在拉伸荷载S为100MPa的作用下,沿与拉伸方向夹角δ为90°的孔边应力数值结果与理论解析解进行比较,带孔平板如图8所示,可以看出在相同位置,数值求解结果与理论Mises应力值的主要误差低于6%,符合精度要求。由此可说明含蚀坑平板在拉伸载荷下的数值分析结果具有一定的准确性。
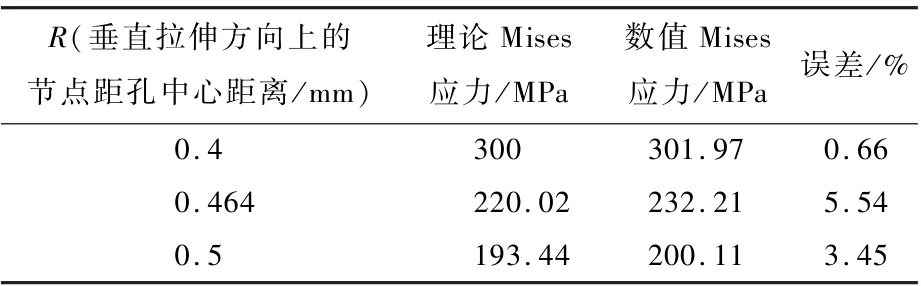
表1 理论与数值Mises应力比较Table1 Comparison of theoretical and numerical Mises stress

图8 带孔平板示意图Fig.8 Schematic diagram of plate with hole
2.2 结果分析与讨论
为探究旋转抛物-锥形蚀坑适用性以及蚀坑应力变化规律,因此设定蚀坑深度h为0.5mm,λ分别为0.8、1.0与1.2,分析不同γ下的蚀坑应力分布。此外,建立长短径分别为m、h的半椭球蚀坑模型作为数值结果对比,进而得到不同蚀坑模型应力数值分析结果。
图9为λ=0.8时的蚀坑局部应力分布。当γ从0.4增长到1.0,蚀坑张开角θ随之增大,即蚀坑从尖深型到浅平型转变过程中,蚀坑局部应力集中带从蚀坑坑底转移至坑口附近。θ较小时(见图9(a)),应力集中带在坑肩以下,且带宽较窄呈长条状分布,应力最大值靠近坑底;随着θ增大,应力集中带分散为两部分分别位于坑肩处,而坑底呈现出应力分布均匀无集中的结果(见图9(b)、(c))。应力数值上,随着θ增大,Mises应力最大值σmax从236MPa降低为213MPa,但是θ=43.60°时,σmax为215MPa与浅平蚀坑应力数值相近,说明蚀坑应力集中带接近时,蚀坑局部应力大小对γ的改变不再敏感。对半椭球形蚀坑,应力集中带带宽较宽且贯穿坑底、坑肩;应力最大值位于坑肩处,数值为202MPa(见图9(d))。由此可知,对于给定m、h的半椭球形蚀坑,无法准确反映不同类型蚀坑的应力集中带,其应力数值结果没有旋转抛物-锥形蚀坑保守。

图9 λ=0.8下的蚀坑局部应力分布Fig.9 Local stress contribution of corrosion pits under λ=0.8
图10为λ=1.0时的蚀坑局部应力分布。当蚀坑为尖深型时(见图10(a)),应力集中带较宽,聚集在坑肩下方的位置且呈轴对称分布;当蚀坑转变为浅平蚀坑时(见图10(b)、(c)),应力集中带分成3部分,一部分在坑底,另两部分对称分布在坑肩两侧;而且γ越大,坑底应力分布带越向坑两侧蔓延。应力数值上,当θ<90°时,σmax为203MPa,当θ≥90°时,由于浅平蚀坑应力带分布相近,σmax为190MPa左右。由此看出,随着λ增大,蚀坑局部应力逐渐降低。对于半椭球蚀坑(见图10(d)),应力集中带仍贯穿坑底与坑口,应力数值仍旧低于旋转抛物-锥形蚀坑的大小。
图11为λ=1.2时的蚀坑局部应力分布。无论是尖深或是浅平蚀坑,其应力分布带与λ=1.0时所对应的蚀坑应力分布大致相同,不同的是应力分布带带宽在θ>90°时更宽更靠近蚀坑两侧;蚀坑σmax数值小,表明λ>1时所引起的应力集中程度低。对于半椭球蚀坑(见图11(d)),应力分布与图10相同,σmax数值基本相同。

图10 λ=1.0下的蚀坑局部应力分布Fig.10 Local stress contribution of corrosion pits under λ=1.0
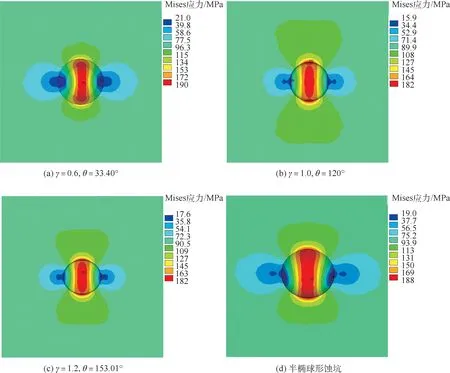
图11 λ=1.2下的蚀坑局部应力分布Fig.11 Local stress contribution of corrosion pits under λ=1.2
综合图9~图11,对于半椭球形蚀坑,其应力分布带都是垂直于拉伸载荷方向且呈左右对称分布。当λ<1时,σmax位置在坑肩,而λ≥1时,应力分布带贯穿坑底至坑口,而且应力大小相近,因此无法判断由蚀坑导致的破坏区域的具体位置,无法衡量坑底、坑肩及坑口的应力集中敏感性,所以半椭球形蚀坑模型在结构安全强度评估上具有一定缺陷。对于旋转抛物-锥形蚀坑模型,λ一定时,随着γ及θ的改变,蚀坑的应力集中分布位置会随之变化。当λ<1.0时,θ较小时,应力集中带在坑肩下方且带宽较窄呈长条状分布,σmax出现在坑底附近;随着θ增大,应力集中带则分散在蚀坑两侧。当λ≥1且θ≤90°,应力集中带在坑肩下方且沿中心轴对称;当θ>90°,应力集中带分为3部分,一部分在坑底附近,其余对称分布在蚀坑两侧,而且随着θ的增大,应力集中带带宽增大,并沿中心轴两侧蔓延。应力分布带的存在说明该处应力集中水平相对其他位置更高,尖深蚀坑应力集中带的连片表明其受载状态下应力集中效应显著,呈现单一局部的特点;而浅平蚀坑应力集中带的分散反映了应力集中的多源性,具有整体性特征,导致裂纹萌生由于应力强度间的竞争关系而被削弱,因此尖深蚀坑会对结构安全产生更为不利的影响。相对于半椭球形蚀坑所呈现的仅仅是贯穿坑底至坑口的应力集中带,旋转抛物-锥形蚀坑能够对不同类型蚀坑引起的应力集中更为准确的判断与评估。
图12反映了在不同λ取值下,应力沿旋转抛物-锥形和半椭球形蚀坑截面曲线的数值分布。对旋转抛物-锥形蚀坑,在图12(a)中,当λ<1.0时,尖深蚀坑截面应力数值(γ=0.4)从坑底到坑口呈现先上升再下降的趋势,其σmax在坑底附近,且坑底处整体应力大小数值较高;而浅平蚀坑截面应力数值分布则截然相反,σmax在坑口附近且坑底附近应力大小较低。图12(b)、(c)中,尖深蚀坑截面应力数值(γ<1)从坑底到坑口呈现先下降再上升然后再下降的趋势,σmax在坑底附近;浅平蚀坑截面应力数值(γ≥1)由坑口附近先下降再上升,但是坑口与坑底附近的应力数值相近,且随着γ的增大,数值上越来越接近相等。而对半椭球形蚀坑,当λ<1时,应力数值由坑底到坑口逐渐增大,σmax在坑口处;当λ≥1时,应力数值由坑底到坑口先增大再减小,σmax在坑口附近。尤为注意的是,2种类型蚀坑坑底处的应力总是小于其附近应力大小,而且应力大小有波动。此外,在蚀坑底部和坑口邻近范围内,应力大小分别沿着蚀坑半长方向单调递减,从而导致应力最大的位置并非在坑口或坑底,而是位于其附近位置。
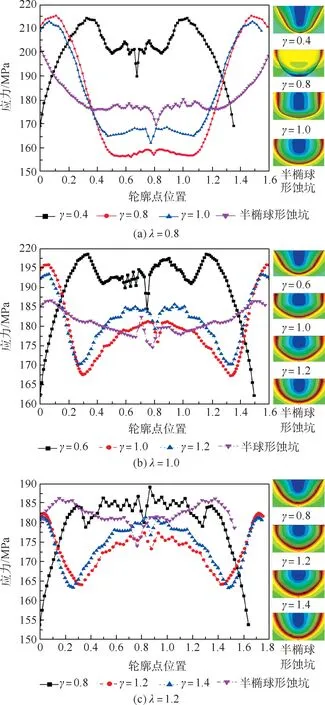
图12 应力沿不同λ值的蚀坑截面曲线分布Fig.12 Stress along corrosion pit sections under various λ value
为衡量旋转抛物-锥形蚀坑的应力集中效应,通过应力集中系数K表征,定量表达式为

式中:σmax和σnorm分别为表示几何形状不连续区域的局部最大弹性应力和远场名义应力。
如表2所示,旋转抛物-锥形蚀坑模型相对半椭球蚀坑的应力集中系数高,得到的结果更为保守,尤其对于尖深蚀坑的应力计算,更能反映尖深蚀坑应力集中的严重程度,有利于对点蚀结构安全强度评价。

表2 旋转抛物-锥形蚀坑与半椭球形蚀坑应力集中系数Table2 Stress concentration factors between rotating parabolic-conial corrosion pit and semi-ellipsoid corrosion pits
3 试验及验证
为进一步探究蚀坑应力集中带在拉伸载荷下的分布情况,因此,对含蚀坑2195Al-Li合金试样进行拉伸试验,并利用SEM对蚀坑拉伸断面进行观测分析。
如图13所 示,采 用 长 为118mm、宽 为25mm、高为4.5mm的6个铝合金拉伸试样,并在其中5个试样中间位置人工构造不同λ、γ类型的蚀坑,同时蚀坑表面进行了光滑处理。根据GB/T228.1—2021金属拉伸试验标准[22],在INSTRON8801拉伸机上以1mm/min速率对试样进行拉伸试验,之后取断裂试样,在Hitachi Su8010扫描电镜上进行断面观察。

图13 拉伸试样及蚀坑形貌SEM图Fig.13 Tensile samples and corrosion pit morphology of SEM
图14为不同λ、γ参数下的蚀坑断面图和对应的有限元应力云图。从断面SEM图中可以看出,2195Al-Li合金以沿晶断裂为主,且内部伴有粗大析出相和细小孔洞,由于这些细观缺陷及层状晶粒分布较为均匀,因此,对不同类型蚀坑断裂源分析及模型验证较为有利。图14(a)、(b)为λ=0.8、γ=0.4时尖深程度较高的尖深蚀坑断面和应力云图,可看出在蚀坑坑底邻近区域由于应力集中导致了断裂产生并伴随着沿晶开裂的现象,蚀坑侧边缘其余位置未发生裂纹萌生,其邻近形貌呈现穿晶断裂的特征,说明蚀坑应力集中位置对材料的使用有较大影响。图14(c)、(d)为λ=1.0、γ=0.6时尖深蚀坑断面和应力云图,表明其应力分布位置与图14(b)近似。从断面上看,起裂位置在蚀坑坑底附近,蚀坑侧边缘没有出现与起裂位置相似的沿晶断裂形貌,其现象与图14(a)一致。但是坑底处留有棱锥状晶粒残留,说明由于坑底应力大小比邻近区域应力数值低,使得坑底处呈现最终瞬时拉断的断裂特征。图14(e)、(f)为λ=1.2、γ=1.2时浅平蚀坑断面和应力云图,不同于尖深蚀坑,其断裂源在坑口附近区域,而位于断裂源以下的蚀坑轮廓断裂特征与尖深蚀坑边缘的断裂形貌基本一致,虽然部分位置毗连着晶间2次裂纹和材料内部微观孔洞等缺陷,但是蚀坑起裂位置仍然位于蚀坑应力最大处。
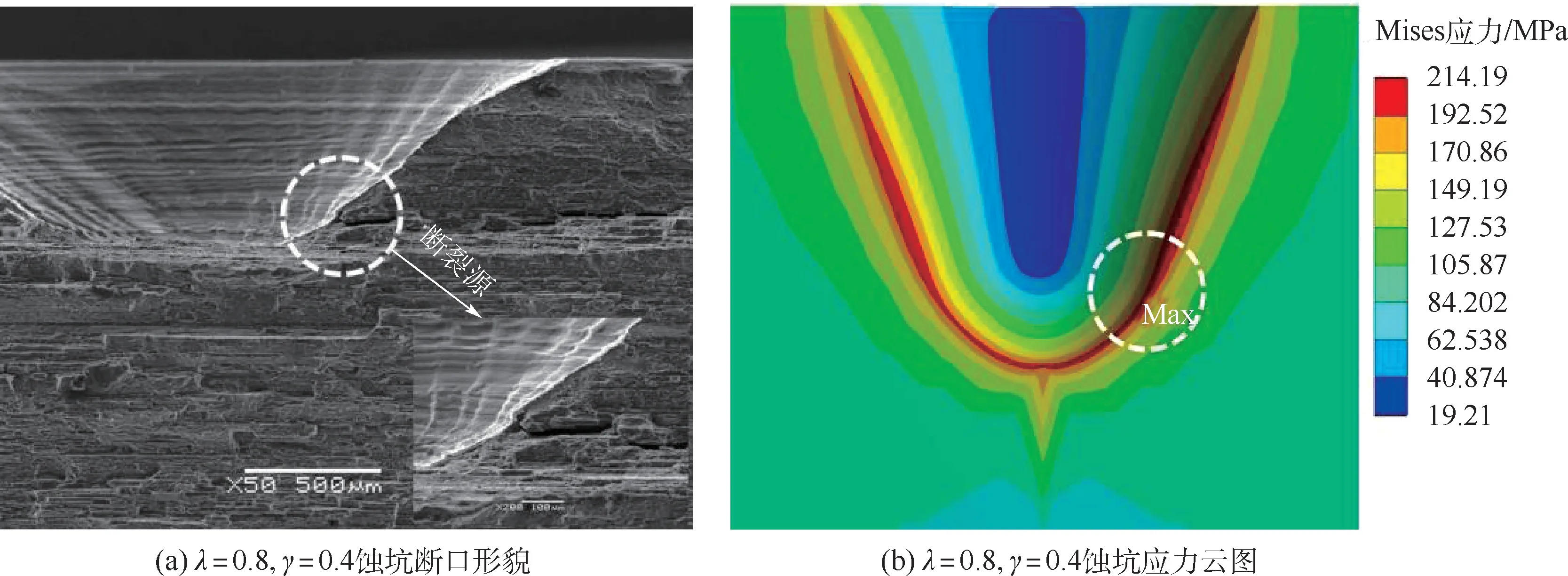
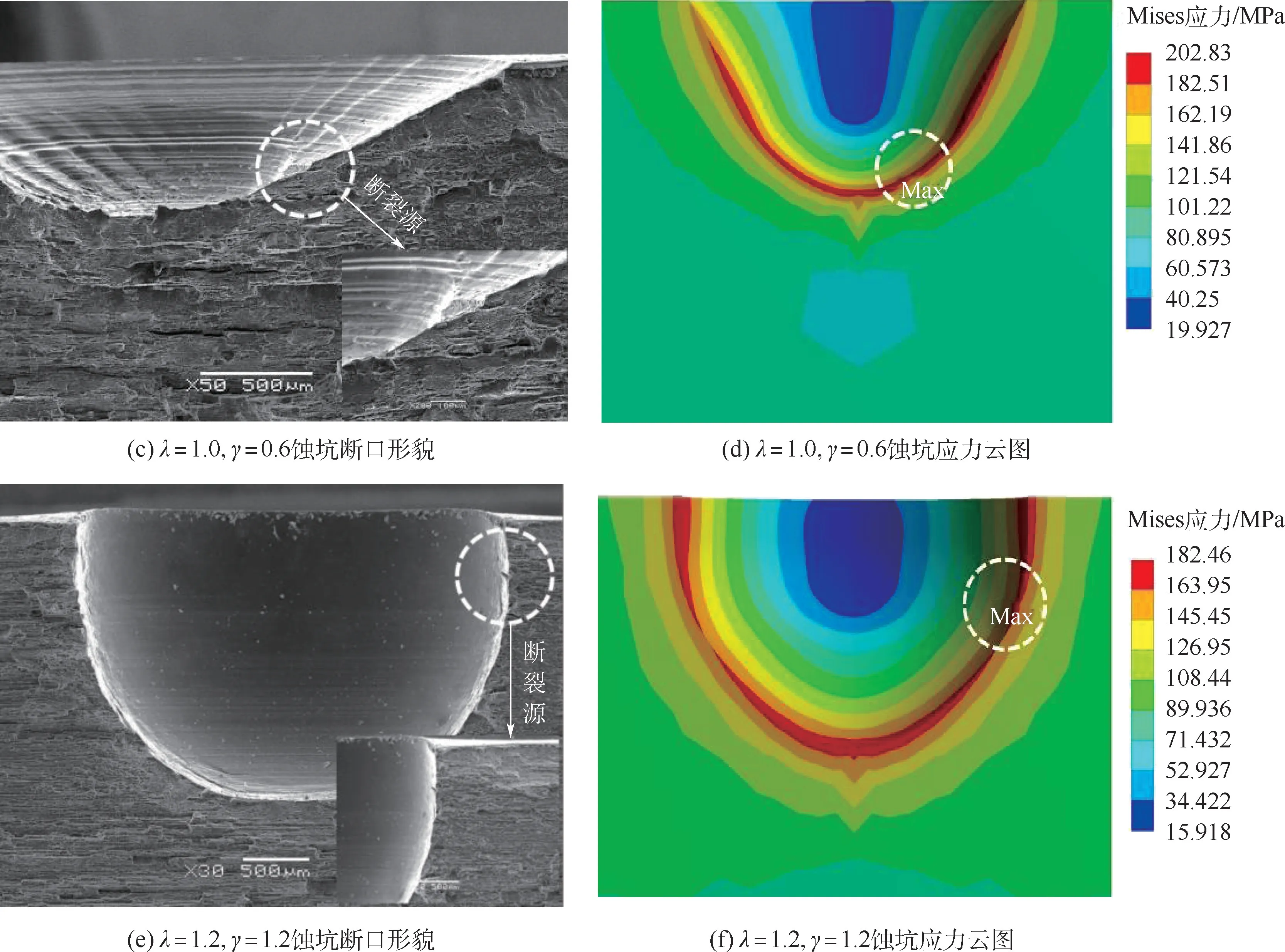
图14 蚀坑断面图与应力云图Fig.14 Cross section and stress contour of corrosion pits
根据不同蚀坑类型的应力分布和断裂形貌,可发现所提出的旋转抛物-锥形蚀坑模型能够应用于不同类型的蚀坑强度分析当中,对起裂位置的判断及适应性上比半椭球形蚀坑模型更为优异。
4 结 论
点蚀是腐蚀环境中金属材料的常见缺陷形式之一。由点蚀引起的应力集中对裂纹的萌生与扩展具有重要影响。因此,准确的蚀坑模型不仅是研究裂纹产生的基础,对结构剩余强度的评价也具有十分重要的意义。为弥补典型蚀坑模型的不足,重新定义了张开角,提出了旋转抛物-锥形蚀坑模型。基于该模型研究了形状比和蚀坑平整度对蚀坑应力集中分布的影响,最后通过含蚀坑铝合金试样拉伸破坏试验验证了模型的正确性。主要的结论如下:
1)无论是尖深型还是浅平型蚀坑,应力集中的极大值点均位于接近坑口或坑底的区域,该区域也是裂纹萌生点。
2)与半椭球形蚀坑模型相比,旋转抛物-锥形蚀坑模型能够准确地表征坑底、坑肩及坑口区域的应力分布及相互之间应力集中的转换规律。
3)拉伸荷载下,尖深蚀坑应力集中的特性大于浅平蚀坑,对材料损伤程度高。
