基于ESO的超局部无模型PMSM转速预测控制

许令亮,陈桂明,李乔扬

(火箭军工程大学 作战保障学院,西安 710025)

永磁同步电机(permanent magnet synchronous motor,PMSM)因其结构简单、体积小和功率密度高等优点,被广泛应用于运动系统中[1-2]。同时,PMSM也是一个多变量、强耦合、非线性的复杂系统,因此,需采用合理的控制方法,提高PMSM的控制性能[3-4]。

传统的控制方法包括矢量控制和直接转矩控制(direct torque control,DTC)。矢量控制借鉴直流电机控制方法,建立旋转坐标变换器,实现交轴和直轴电流的解耦,进而实现磁场和转矩的解耦。但是随着电机的运行,电机参数会受到温升、磁场饱和运行状态等影响,产生参数漂移,导致模型失配,降低电机的控制性能,此时矢量控制技术难以满足实际工作需要[5-6]。为了解决这个问题,马玉梅等[7]将滑模控制和比例积分(proportional integral,PI)控制结合,有效利用滑模控制对参数变化的不敏感性和PI控制的稳定性,结果表明,该方法能够有效跟踪额定转速,启动时间短,超调量较小。DTC控制摒弃了矢量控制解耦的思想,取消了旋转坐标变换器,减弱了控制模型对参数的依赖,建立磁链和转矩调节器,输出所需的的空间电压。但是,DTC控制存在逆变器开关不恒定、输出转矩磁链脉动较大及因转矩脉动带来的高频噪声等[8-9]。Xia等[10]通过构造增强型切换表,建立了转矩、磁通变化率和矩阵变换器之间的解析表达式,无须坐标转换,并且具有固定的逆变器开关频率,结果表明,该方法能够有效降低转矩脉动。

相比于传统控制方法,模型预测控制方法因其结构简单,易于实现,控制效果好,受到国内外学者广泛关注。模型预测控制方法利用控制对象的数学模型,离散化得到下一时刻预测值,再通过优化成本函数,使得预测值沿着参考轨迹趋近于期望值。但是模型预测控制方法依赖于控制对象的数学模型,在电机运转过程中,会受到内部参数漂移和外部未知干扰,导致控制性能下降,控制精度降低[11-12]。为了解决这些问题,刘珅和高琳[13]提出了改进型模型预测直接转矩控制方法,通过无差拍控制理论,计算出期望电压矢量,根据引入的虚拟电压矢量,确定期望电压所在扇区,进而求出实际电压矢量,结果表明,该方法能够有效抑制转矩和磁链脉动,提高模型鲁棒性。贾成禹等[14]提出了一种线性变参数模型预测控制算法,设计增量形式的预测模型及代价函数实现了转速的最优调节,从而克服因模型参数不匹配及外部扰动引起的稳态误差,实验结果表明,该方法具有良好的转速动态稳定性。

为了降低参数漂移对控制模型的影响,Fliess和Join[15]提出了无模型控制方法,该方法只利用系统的输入和输出,不考虑任何参数,将已知项和未知项干扰统称为系统总扰动,规避了系统参数对控制性能的影响,降低了模型对参数的依赖性,提高了控制性能。Zhou等[16]提出了超局部无模型和无差拍预测控制方法,利用速度环的输入和输出变量建立了超局部控制模型,结果表明,该方法能有效提高模型鲁棒性,有较强的抗干扰能力。Zhou等[17]建立了超局部无模型控制模型,针对系统总干扰项,利用参数辨识的方法在线进行估计,并进行前馈补偿,结果表明,该方法在一定程度上降低了电流纹波,提高了系统动态响应性能。

为了提高PMSM系统对参数变化、内部干扰和外部干扰的鲁棒性,获得更好的转速跟踪效果,本文提出超局部无模型转速预测控制(model-free speed prediction control,MFSPC)。利用速度环的输入和输出,不涉及任何系统参数,针对系统总扰动和数字控制系统存在的一拍延迟,建立扩张状态观测器(extended state observer,ESO),实时监测系统总扰动,并进行前馈补偿,利用ESO的预测转速弥补数字控制系统存在的一拍延迟。同时,采用频域分析方法,对ESO参数进行整定。实验结果表明,本文方法能够实现快速的动态响应,降低转速脉动,减小电流纹波,有较强的鲁棒性和抗干扰性。

1 PMSM参数敏感性分析

根据磁场定向理论,PMSM数学模型为

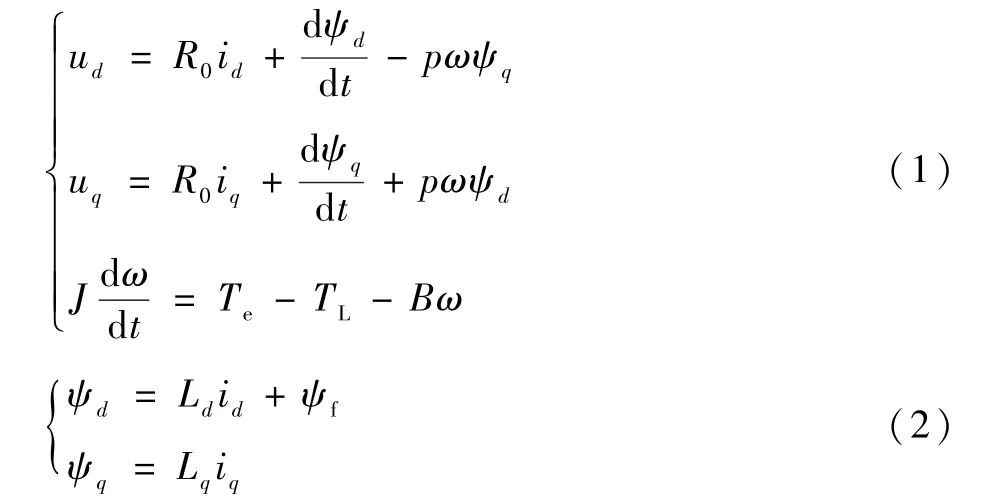
式中:ud和uq分别为d-q轴电压;id和iq分别为d-q轴电流;ψd和ψq分别为d-q轴磁链;Ld和Lq分别为d-q轴电感;R0为定子电阻;ψf为永磁体磁链;p为电机极对数;ω为机械角速度;B为摩擦系数;J为转动惯量;Te为电磁转矩;TL为负载转。

将式(2)代入式(1)得到定子电压方程为

从式(3)可以看出,PMSM数学模型实现了解耦。此时电磁转矩方程可写为

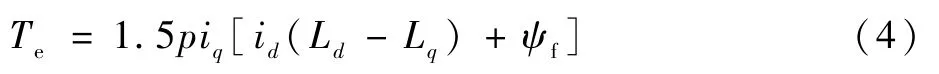
对于表贴式PMSM,Ld=Lq=L0,此时,运动方程为

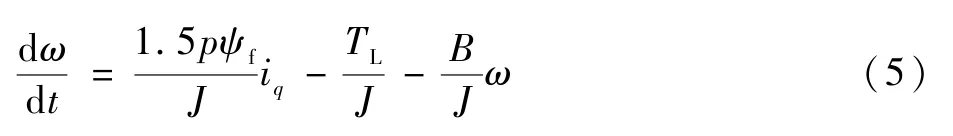
根据前向欧拉离散法,对式(5)进行离散化,得到k+1时刻预测值:

式中:A=(1.5pψf0)/J;Ts为采样时间。

随着电机运转,电机参数会发生变化,产生参数漂移,此时,电机参数实际值和电机铭牌上的标称值不相等。当电机参数为实际值时,此时理想的速度环输出电流为

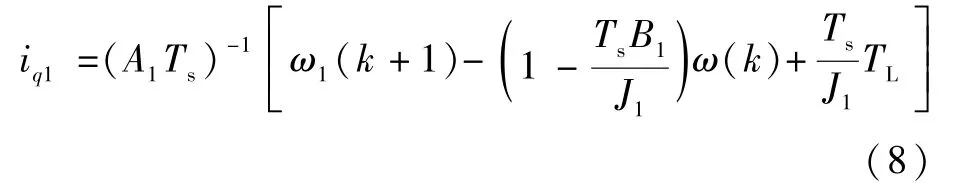
式中:A1=(1.5pψf1)/J1;ψf1、J1和B1为电机参数的实际值;ω1为理想机械角速度。

但是在实际计算过程中,无法精确测量随时间变化的电机参数真实值,因此采用电机铭牌上的标称值。此时实际的速度环输出电流为

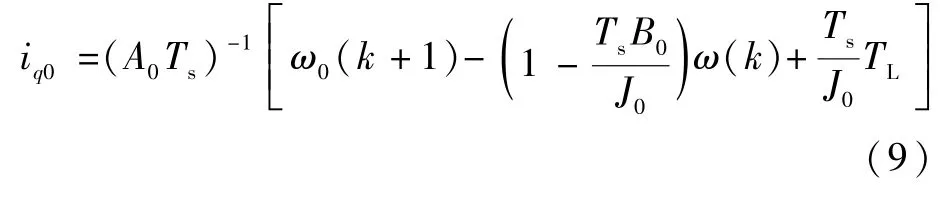
式中:A0=(1.5pψf0)/J0;ψf0、J0和B0为电机铭牌上的标称值;ω0为实际机械角速度。

令速度环输出电流相等,即式(8)和式(9)相等,得到两者预测转速之间的关系为

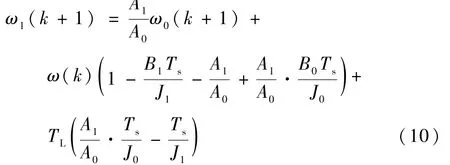
由式(10)可知,摩擦系数、转动惯量和永磁体磁链失配对预测转速均有影响。为了解决参数漂移导致的模型失配问题,提出超局部MFSPC方法。

图1表示在转速1000r/min和负载转矩10N·m条件下,转动惯量J、摩擦系数B和磁链ψf失配对速度环造成的误差ΔE影响。可知,3种参数失配均影响着速度环的稳定性,转动惯量和摩擦系数失配对速度环的影响较大,而磁链参数失配引起的误差影响较小。

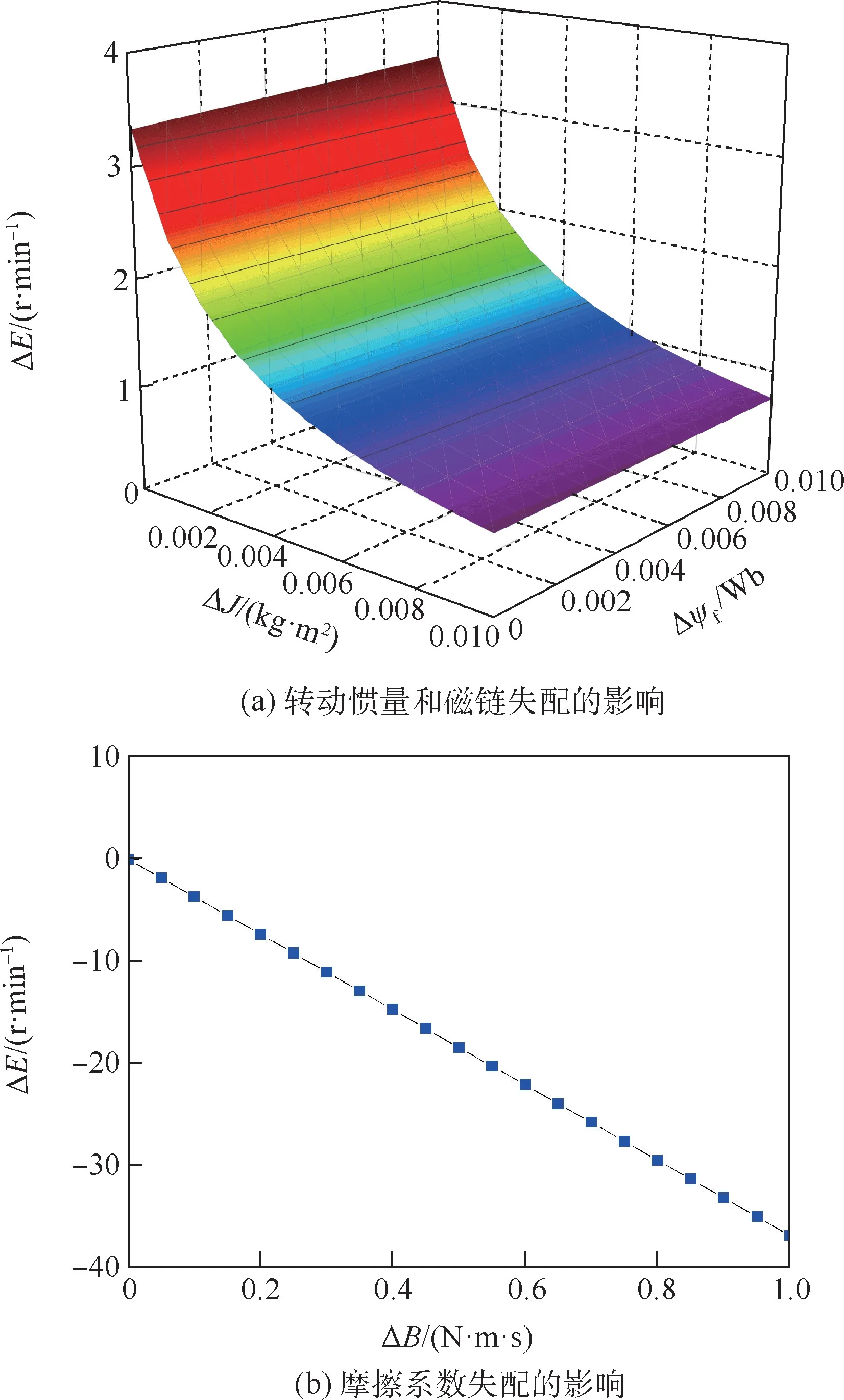
图1 1000r/min和10N·m条件下参数失配造成的误差影响Fig.1 Effect of errors caused by mismatch parameters at 1000r/min and10N·m

2 超局部无模型转速预测控制

2.1 超局部模型

针对一阶系统输入和输出,传统的超局部模型为[15]

̇y=W+au(11)

式中:y为系统输出;u为系统输入;W为系统已知干扰和未知干扰总和;a为模型结构的非物理比例因子。

式中:e=y*-y为跟踪误差。

当采用P控制器时,则式(12)可表达为

式中:Kp为比例增益。

2.2 转速预测控制模型

考虑参数变化和未知扰动,式(5)变为

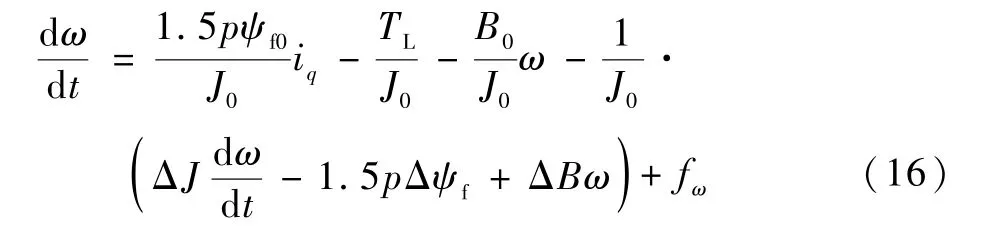
式中:ΔJ=J1-J0;ΔB=B1-B0;Δψf=ψf1-ψf0;fω为未知扰动。

根据式(16)将iq作为系统输入、ω作为系统输出,建立超局部无模型控制结构:

式中:a为控制器增益;F为系统总扰动,包括系统参数漂移扰动项和未知扰动项。

采用前向欧拉离散法,对式(17)进行离散化,将连续时间模型转化为离散时间模型,得到

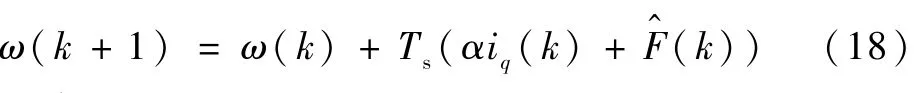
再求电流iq:

式中:F^为F的估计值。

为使转速更好地跟踪额定转速,令

最终求出参考电流为

另外,由于数字控制系统存在一拍延迟现象,如果在控制器中不加以考虑,将会降低控制系统性能[18]。为了解决数字控制系统一拍延迟问题,建立ESO模型结构,弥补一拍延迟。

3 建立ESO结构模型

基于式(17),选择iq和F作为状态变量,建立ESO,其状态空间方程为[19-20]

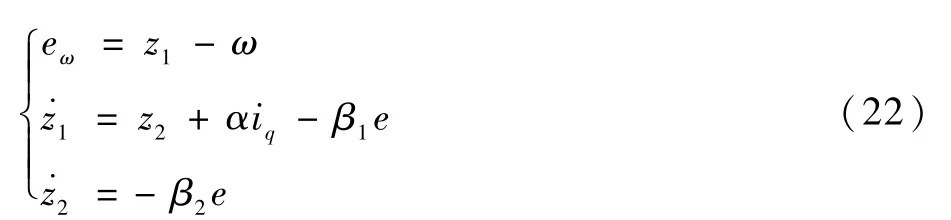
式中:eω为速度环跟踪误差;β1和β2为ESO增益系数;z1为ω的估计值,即z1=;z2为F的估计值,即z2=。

将式(22)进行S变换,得到

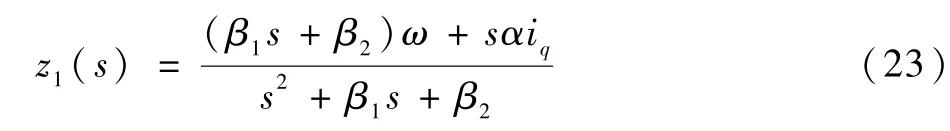
根据式(23)可以得到特征方程为

为使系统处于稳定状态,特征根为-ω0,ω0为ESO的带宽,因此,ESO增 益 系数β1和β2为

采用前向欧拉离散法,对式(22)进行离散化,得到离散化状态空间方程为

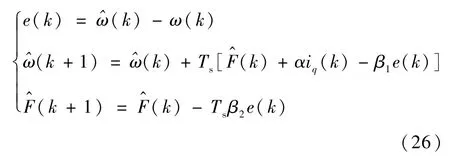
为了验证离散化状态空间的稳定性,对式(26)进行Z变换,得到

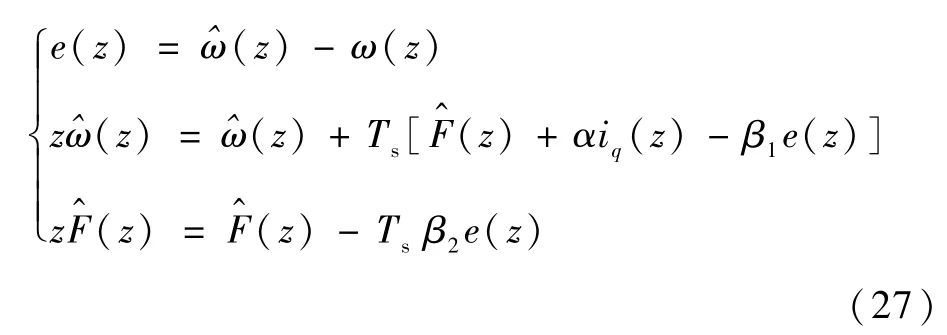
考虑到采样时间足够小,则离散系统的传递函数为

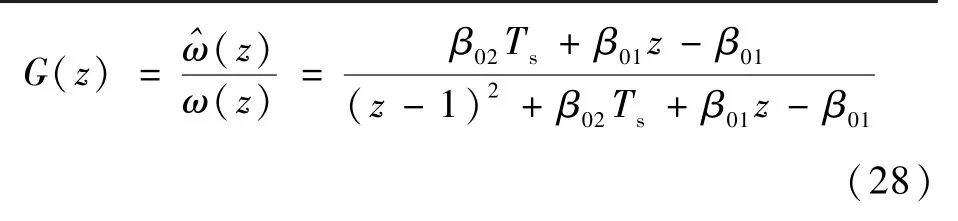
式中:β01=β1Ts;β02=β2Ts。

要想保证离散系统的稳定性,则离散系统的极点必须处于单位圆内,因此离散系统的特征方程为

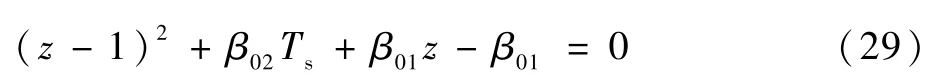
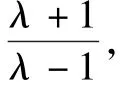
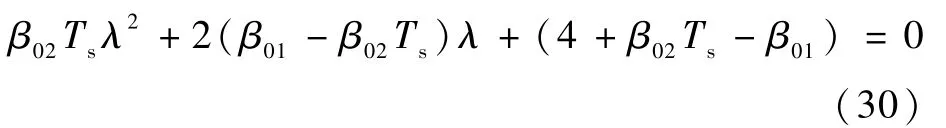
根据劳斯·赫尔维茨判据准则,λ域特征方程的各系数均大于0,则离散系统稳定,进而求得ESO增益系数的取值范围,即

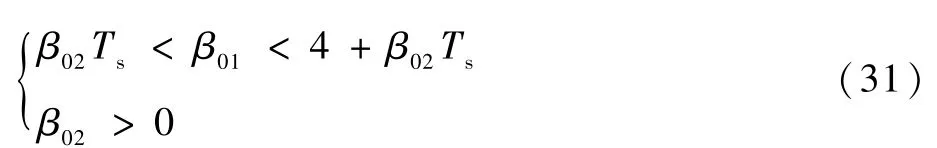
在PMSM控制系统中,为了获得良好的控制效果,速度外环的带宽小于电流内环[22]。图2为系统控制结构。

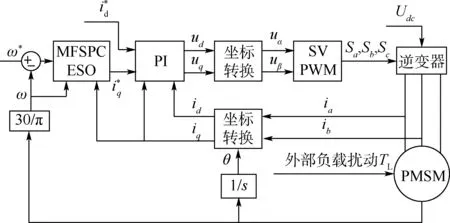
图2 基于MFSPC+ESO方法的PMSM驱动系统控制Fig.2 PMSM drive system control based on MFSPC+ESO method

4 延迟补偿

为了弥补数字控制系统中的一拍延迟问题,将式(21)中的采样转速ω(k)和(k)替代为式(26)中的和(k+1)和(k+1)。

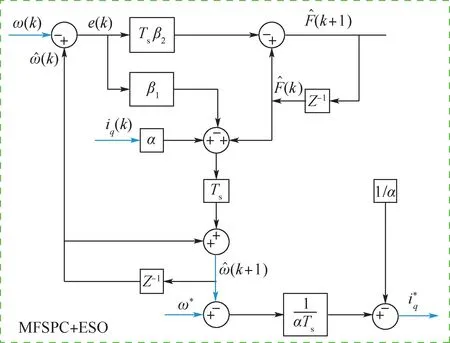
图3 基于ESO的MFSPC转速预测控制Fig.3 Speed predictive control of MFSPC based on ESO

5 实验结果分析

PMSM驱动控制系统的实验配置如图4所示,实验平台如图5所示。该实验平台基于MATLAB/Simulink进行伺服控制系统算法模型设计,并能够自动生成代码,通过开发软件下载到目标机上运行,便于PMSM控制方法的研究和验证。PMSM模型的参数如表1所示。

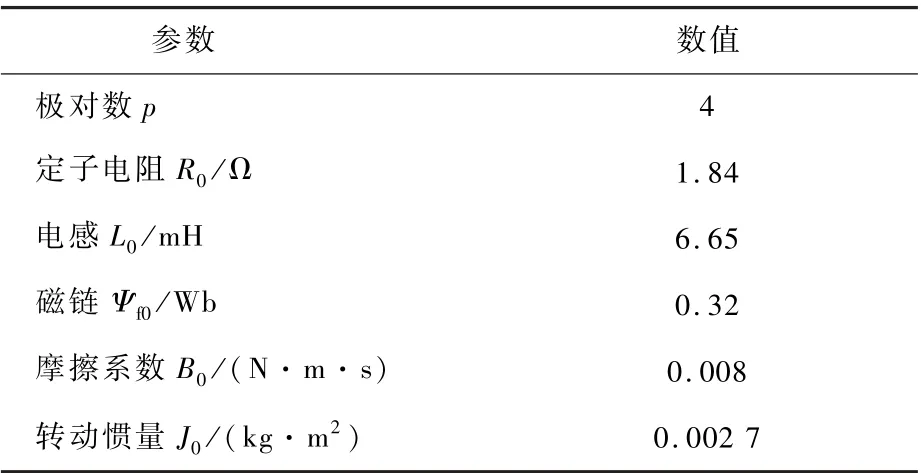
表1 PMSM模型参数Table1 Parameters of PMSM model

图4 PMSM实验平台配置Fig.4 PMSM experimental platform configuration

图5 PMSM实验平台Fig.5 PMSM experimental platform

为体现所搭建模型的控制性能,将MFSPC+ESO方法与传统PI方法、传统MFSPC方法、基于终端滑模控制(terminal sliding mode control,TSMC)的MFSPC方法(MFSPC+TSMC)[23]结果相比较,并进行分析。MFSPC+ESO方法控制参数α=4000,ω0=100rad/s;PI控制器增益参数Kp=0.14,K=14;MFSPC+TSMC方法控制参数μ1=1,μ2=5,σ1=0.9,σ2=0.5。

5.1 速度环的反转性能测试

图6为在额定转速1000r/min下电机反转的响应波形。

由图6(a)MFSPC+ESO方法的电机转速响应可以看出,在电机启动阶段,几乎未产生超调,平稳启动,能够快速地达到给定转速,具有较快的动态响应,在正常运行阶段,没有产生明显的转速脉动,运行平稳。同时,图6(b)、(c)在电机启动阶段,转速抖振现象较为严重,图6(d)传统PI方法的转速产生了较大超调,不利于电机的正常启动。MFSPC+ESO方法和传统PI方法的d-q轴电流运行较为平稳,虽然在启动阶段产生了过冲,但是能够快速回归正常,其中MFSPC+ESO方法产生的电流过冲较小,表现出良好的动态特性。而传统MFSPC方法的q轴电流出现了失真,脉动较为明显,MFSPC+TSMC方法的q轴电流产生较大的电流纹波。当电机反转时,MFSPC+ESO方法能够快速跟踪转速,有较快的动态响应特性,产生稳定的d-q轴电流,另外3种控制方法速度反转时,波动明显,d-q轴电流失真,不能平稳运行。

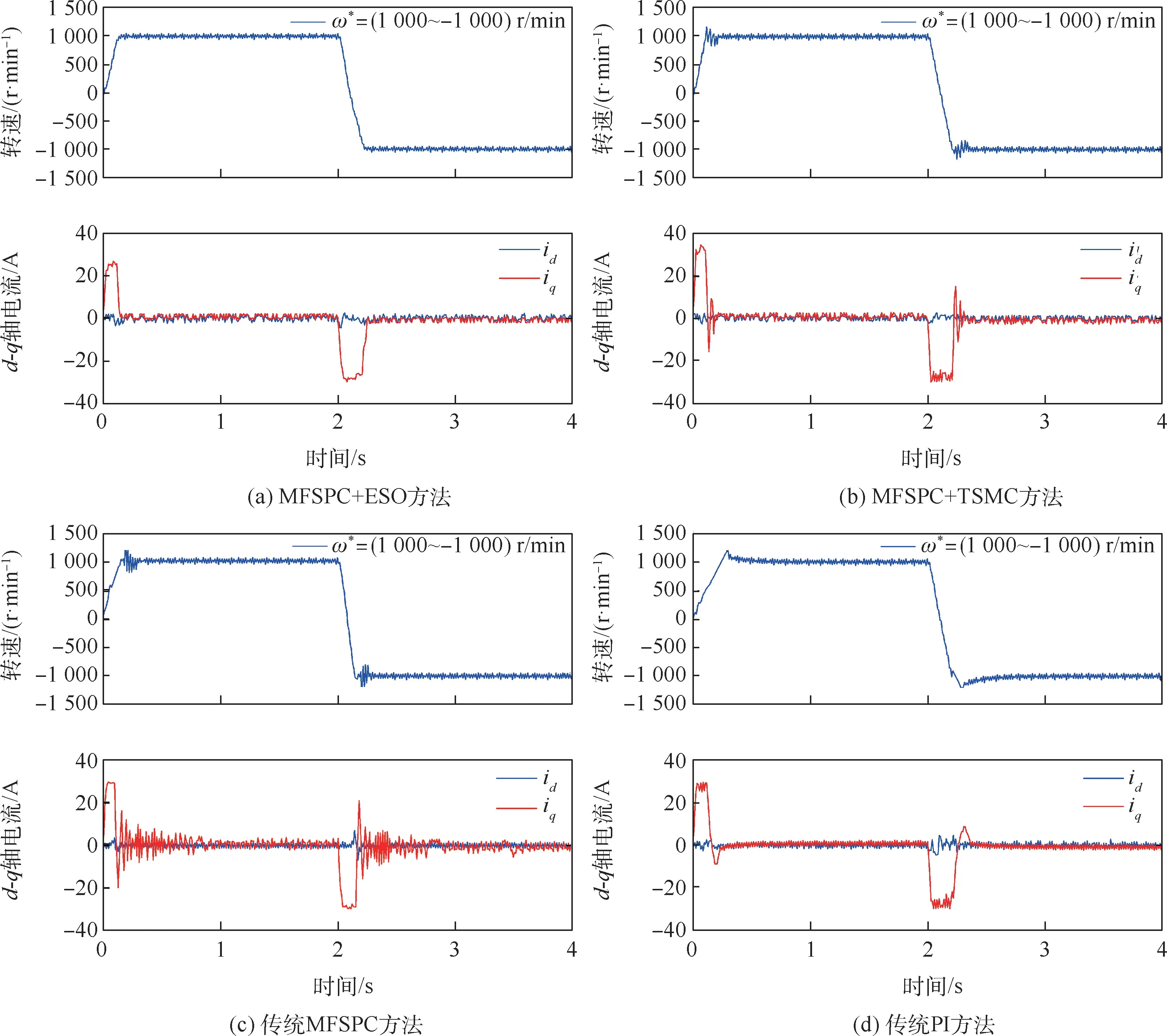
图6 四种控制方法的反转性能对比Fig.6 Comparison of reversal performance of four control methods

表2为速度反转特性。可知,MFSPC+ESO方法相比另外3种控制方法,转速超调量较小,在整个电机运行中,转速的波动方差较小,当电机反转时,回归正常转速的时间最小,表现出较好的稳定性和快速响应能力。

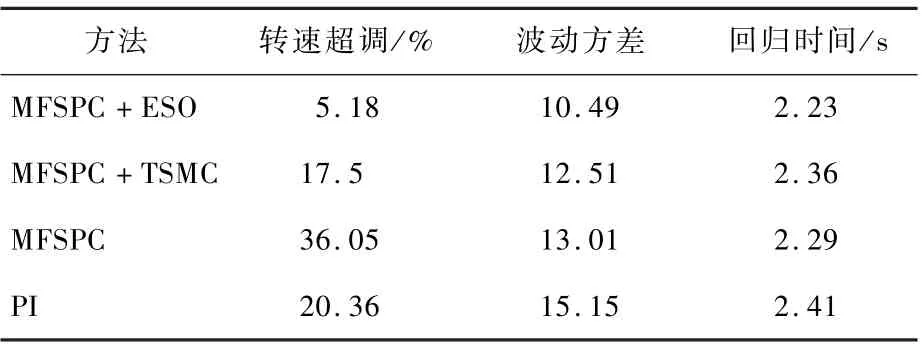
表2 速度反转特性Table2 Speed reversal characteristics

5.2 速度环的负载扰动性能测试

在宽速范围,加入10N·m的外部负载扰动,电机转速的响应波形如图7所示。分别设置额定转速的10%、80%、150%。由图7可知,在宽速范围内,MFSPC+ESO方法能够平稳运行,在受到负载扰动时,转速下降较小,并且能够快速回归正常转速,表现出良好的跟踪和抗干扰性能。而MFSPC+TSMC方法,在低速为100r/min时,转速失真,无法稳定精确跟踪给定转速,但是图7(b)、(c)在受到负载扰动时,转速所受影响较小。传统PI方法在低速100r/min时,抖振较为明显,波动较大,当加入负载扰动时,转速下降较大,抗干扰性能较低。

图7 四种控制方法的负载扰动性能对比Fig.7 Comparison of load disturbance performance of four control methods

表3为在负载扰动下4种控制方法的速度超调和失调特性。可知,传统PI方法在电机启动时产生超调较大,当受到负载扰动时,失调也较明显;传统MFSPC方法和MFSPC+TSMC方法,在启动过程中产生了较大抖动,当受到负载扰动时,表现出一定的抗干扰能力;MFSPC+ESO方法表现出较好的抗干扰性能。

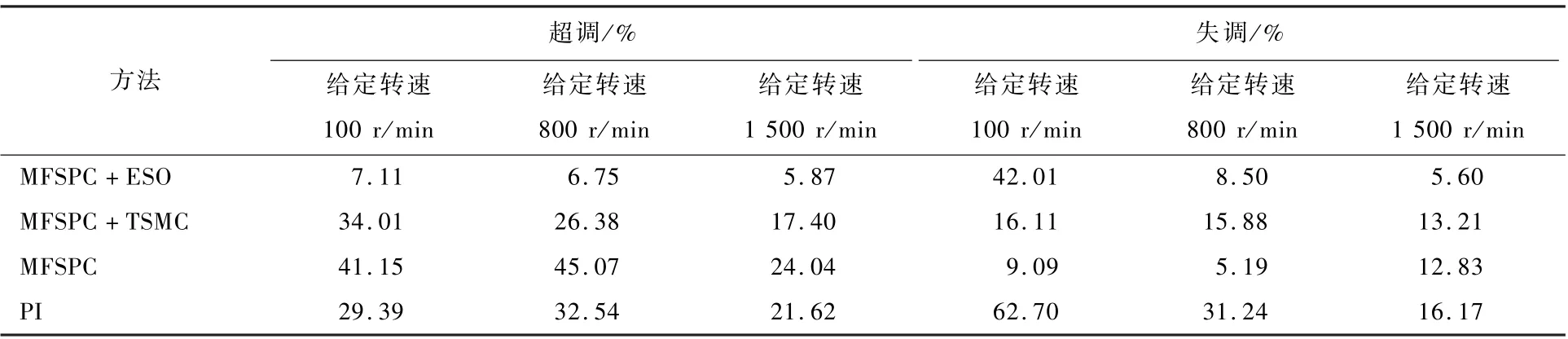
表3 速度响应特性Table3 Speed response characteristics

图8为4种控制方法在额定转速1000r/min下加入额定负载15N·m的转速响应曲线。可知,在电机启动阶段,相比于另外3种控制方法,MFSPC+ESO方法启动平稳,几乎未产生超调。当t=2s时,加入额定负载,MFSPC+TSMC方法和传统MFSPC方法震荡较为明显,脉动比较大;传统PI方法受负载影响较大,失调较大;而MFSPC+ESO方法,转速下降较小,并且能够较快恢复正常,有较好的抗干扰性和较快的动态响应。

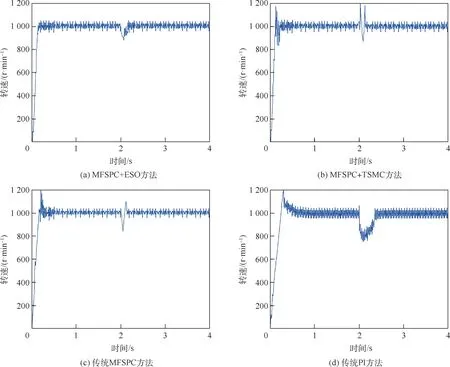
图8 额定负载下的转速响应对比Fig.8 Comparison of speed response under rated load

5.3 速度环的参数变化性能测试

当PMSM控制模型受到参数变化影响时,系统的控制性能下降。为了验证搭建模型的鲁棒性和抗干扰性能,设置PMSM参数磁链ψf=ψf0→0.8ψf0,摩擦系数B=B0→2B0,转动惯量J=J0→2J0并且加入负载扰动TL=10N·m。

图9为在变参数和外部负载扰动条件下4种控制方法的响应波形。MFSPC+ESO方法始终表现出良好的鲁棒性和抗干扰性能。在启动阶段,传统PI方法出现较大超调,MFSPC+TSMC方法和MFSPC方法出现较大脉动。当受到参数变化和外部负载扰动时,传统PI方法出现了较大失调,转速下降明显,而传统MFSPC方法出现了较大的转速脉动,运行不平稳,MFSPC+TSMC方法无法准确跟踪额定转速,运转速度低于额定转速。d-q轴电流在受到参数变化和负载扰动时,MFSPC+ESO方法能够迅速跟踪,没有产生较大的电流纹波,动态特性较好,另外3种控制方法的电流响应波动较大,脉动较明显。

图9 四种控制方法的参数变化性能对比Fig.9 Comparison of parameter change of four control methods

表4为4种控制方法的实现复杂度比较。MFSPC+ESO方法与传统PI方法相比,不需要电机参数,各方面性能提高较大。与传统MFSPC方法和MFSPC+TSMC方法相比,MFSPC+ESO方法仅需调节2个控制参数,工作量较低,表现出较强的鲁棒性和抗干扰性,转速和电流脉动较小,跟踪精度较高,表现出较优的性能。

表4 四种控制方法实现复杂度比较Table4 Comparison of implementation complexity of four control methods

6 结 论

1)针对因电机参数漂移和外部扰动导致的电机控制性能下降,本文提出了超局部MFSPC方法,该方法不涉及任何电机参数,能有效降低模型对参数变化的敏感性。

2)对于系统总扰动和数字系统中的一拍延迟,建立了ESO,估测系统总扰动,进行前馈补偿,并利用无差拍控制原理,解决了一拍延迟问题,以提高控制精度

3)将结合ESO的MFSPC方法与其他3种方法进行对比实验,结果表明,MFSPC+ESO方法工作量较小,能够平稳启动,当受到扰动时,有较快的动态响应速度,能够准确跟踪额定转速,有较强的鲁棒性和抗干扰能力。