中国赋役史中的理念、制度与技术——从“均平”角度的重新审视

郭永钦 申 斌

(1.广州大学 人文学院， 广州 510006；2.广东省社会科学院 历史与孙中山研究所， 广州 510635)

制度史是中国史研究的重要领域，近年学界围绕着“活”的制度史、制度史观、日常统治史等议题，涌现出众多重要论著。(1)邓小南：《走向“活”的制度史——以宋代官僚政治制度史研究为例的点滴思考》，《浙江学刊》2003年第3期；阎步克：《中国古代官阶制度引论》，北京：北京大学出版社，2010年，第7-9页；侯旭东：《传舍使用与汉帝国的日常统治》，《中国史研究》2008年第1期；邓小南：《再谈走向“活”的制度史》，《史学月刊》2022年第1期。近年已经有学者对制度史作为研究领域的形成史加以反思，参见侯旭东：《“制度”如何成为了“制度史”》，《中国社会科学评价》2019年第1期。这些研究或注重制度的实践过程及人事关系，或阐发制度内在的机理、结构，或突出以人的能动性为观察视角。(2)孙正军：《何为制度——中国古代政治制度研究的三种理路》，《中国社会科学评价》2019年第4期。制度的设计和演进背后必定蕴含着某种思想观念，而其具体实践又需要一系列社会治理技术(如文书、会计等)的支撑。观念正是人的能动性和社会结构的制约性的结合点，而技术因素则更能彰显制度运行的底层结构。因此，揭示传统中国观念、制度、技术的内在关联性，应是丰富、深化制度史研究的有效路径。尤其是从社会治理技术因素来解读观念和制度的影响，对阐释中国文化实践的内涵十分重要，然而此前从该角度的探讨颇为不足。

古代国家和社会秩序构建遵循的政治理念不但塑造了君民头脑中的“正义”观，也制约着制度设计的导向与框架，还渗透到制度实施所依托的技术性知识中。在中国古代，“均平”就是这种关键性政治理念。它影响着统治者、士人、民众的思想认知，体现在财产分配、赋役征发等诸多制度环节中，甚至渗透到了服务于赋役核算的算学技术层面。我们可以由此观察政治经济思想、赋役制度和算学技术知识三者的内在关联和一致性，从算学知识中解读观念的渗透与制度的影响，为前述研究路径提供一个方法性案例。

一、均平：传统中国的秩序正义

“均”或“均平”是传统理想社会秩序的一个核心理念，具体表现为财富分配和税负分派的指导性原则，学界对此已有论断。(3)李振宏：《中国古代“平均赋役”的文化考察》，《学术界》2005年第2期；李振宏：《中国古代均平文化论纲》，《学术月刊》2006年第2期。但对古人语境中“均平”与“平均”的内涵差异仍有进一步申论的必要。一般认为，“均”有两种不同内涵：其一是儒家所主张的以差等(等级差异)为前提的均平，其二是百姓理想当中无差别的绝对平等、平均。(4)山田胜芳：《中国のユートピアと「均の理念」》，东京：汲古书院，2001年。下文着重分析在大多数历史语境下，后者可能并非民众的真实诉求，前者也并非专为儒家独有的主张，而是传统社会所追求的理想秩序。

民众的绝对平均主义集中体现在农民起义的主张和诉求当中。自秦汉到隋唐，这种思想还混杂在民间宗教意识中。唐末以降，平均主义思想才日渐鲜明。唐末农民起义军首领王仙芝自称“天补平均(一作均平)大将军”；北宋王小波起义明确提出“吾疾贫富不均，今为汝辈均之”；南宋钟相起义，以“法分贵贱贫富，非善法也，我行法，当等贵贱、均贫富”来发动农民；明末李自成起义以“均田”“免粮”为号召；太平天国《天朝田亩制度》中“无处不均匀”的理想设计达到顶峰。

对这种平均主义思想，有三点值得注意。第一，农民起义的诉求是反对现实社会中的贵贱贫富格局，但未必要废除这种社会结构，更多是希望改变自己被压迫、被剥削的地位。第二，从实践上看，农民军事实上实行的也并非绝对平均主义，而仍是有差等的制度和政策。譬如《天朝田亩制度》同样包含严格的等级制度，权力差异在各方面都有体现。第三，绝对平均主义会破坏一般的农民私有财产，反而打击了起义参与者的积极性。总而言之，政治上绝对平等、经济上绝对平均的“平均主义”，即便对百姓而言大多也只停留在幻想和口号中，未必源自生活实态。所以，绝对平均主义不但事实上从未实行过，也非民众的真正诉求。

本文认为传统思想中的“均”并非指财富一律均等，而是以各安其分为前提、有差等的均平。这一主张，是以承认事物差异乃是自然之理为前提的，即“物之不齐，物之情也”(《孟子·滕文公上》)。该理念从分配角度说，是财富的分配与社会身份相适应；从汲取角度说，是赋役征发与被征收者的身份地位和财产情况相适应。(5)在欧洲前古典经济学时期，围绕财产正义、分配正义、税收正义也有诸多讨论，涉及“正义”(justice)、“公平”(fairness)、“平等”(equality)关键概念，形成“量能”“受益”“均等牺牲”“一致同意”等不同的税负公平原则。公平和正义是普世性的价值追求，但需要结合不同社会历史环境来认识。将欧洲这些思想和实践与我国的均平思想和实践进行比较，是非常有意义的话题。这一思想最终体现在传统中国土地赋役制度设计上。

二、均田、户等、鼠尾：均平原则在土地赋役制度上的体现

如刘志伟所言，中国王朝的贡赋体制合理化的基本原则就是均平。(6)刘志伟：《中国王朝的贡赋体制与经济史》，《贡赋体制与市场：明清社会经济史论稿》，北京：中华书局，2019年，第25页。对均平原则的追求在传统社会中是一贯的，然而贯彻该理念的方式却随着时代发展而改变。有两个变化最为突出：一是重心从晋唐时期的财产分配制度向唐两税法以降的赋役征发制度转移，二是从追求理论最合理的制度逐渐向致力实践中防弊的制度转变。

第一个变化体现了均平的制度设计从分配向征收方面转移。不过，无论是分配生产资料的均田制，还是以资产为宗的两税法，抑或以户等为依据的差役分派，均体现出以差等为前提的均平理念。

在汉唐之间，王朝国家在考虑均平问题时多从社会政策着眼，赋税制度与生产资料的分配制度(更确切地说是土地分配限额制度)是结合实行的。国家对不同身份等级的人占有土地有限额规定，有条件时还进行给田、授田等，从而确保编户齐民拥有与其身份相适应的土地(生产资料)，并据此为国家纳粮服役。汉代《二年律令》就规定了基于爵制身份等级的不同给田额度。西汉末期开始出现的所谓“均田之制”在设计理念上仍然是基于爵制、品秩差等来进行授田，而非一律均等的给田制。西晋时期与户调式并行的占田额、课田额规定亦以官品差等为依据。(7)关于占田、课田如何理解，学界多有争论。但是其额度制定体现了基于身份差等的财产合理性差异观念这一点当无疑问。北魏孝文帝行均田制，明确进行官授田操作，唐代均田制则集其大成。但是这种“均田之制”，并不能简单理解为“每名正丁(成年男子)授田百亩”这种无差别等额授田的平均主义，其完整内涵是根据爵位、品级、职分的差别而确定不同的受田面积。(8)渡边信一郎：《传统中国的均平秩序——以经济秩序为中心》，周东平、朱腾主编：《法律史译评》第6卷，上海：中西书局，2018年，第1-11页。另外，关于均田制的实际实施地域范围、普遍程度、贯彻力度学界存在争议，但对晋唐时期国家曾推行此种生产资料再分配政策这点应无分歧。本文着眼于制度设计的讨论，不涉及实际执行的争议问题。

自从唐德宗时杨炎两税法以降，国家放弃了从生产资料分配角度贯彻均平的方针，转而在承认财产占有现状的前提下，从赋税征收角度体现均平原则，即参考人户的社会身份以及土地肥瘠、财力厚薄、人丁多寡等差异因素后合理派征。两税法下，两税斛斗计亩而征；两税钱则根据户等高低(其实是资产多寡)配征(9)陈明光、孙彩红：《隋唐五代财政史》，长沙：湖南人民出版社，2015年，第416-418页。，即所谓以资产为宗，以贫富为差。自此，贯彻均平的焦点转向了税制设计环节。北宋因袭了两税法以后的政策取向，“田制不立”，(10)关于宋代“田制不立”的含义，学界存在争议。笔者认为主要指的是国家不再实行晋唐时期的土地再分配政策。参考杨际平：《宋代“田制不立”、“不抑兼并”说驳议》，《中国社会经济史研究》2006年第2期；耿元骊：《宋代“田制不立”新探》，《求是学刊》2009年第4期；杨际平：《〈宋代“田制不立”、“不抑兼并”说〉再商榷——兼答薛政超同志》，《中国农史》2010年第2期。注意力集中到赋税能否完纳问题上。由于可持续的赋役征发的需要，国家又必须关注赋役能否“均平”地分派给编户齐民的问题。而客观上，北宋政权也不掌握大量无主荒地，官无闲田，无法开展土地再分配。

宋代开始，役的重点发生转移，从古代的“力役之征”变为“庶人在官”，所要求的不仅是体力，而且负担加重。(11)吕思勉：《中国通史》，上海：上海古籍出版社，2009年，第126页。因此，晚唐以后逐渐形成以户为单位综合评定人丁财产多寡，确立等次，作为派役依据的做法。无论是元代论人户物力，还是明代论人丁事产均不出该原则。户等制在这一背景下发展起来，并成为在差役征发中贯彻均平原则的制度工具，直到明前中期一条鞭法后才逐渐式微。(12)邢铁：《户等制度史纲》，昆明：云南大学出版社，2002年，第56-156页。

在户等制下，依据户等编制册籍，按照上等户应重役，下等户应轻役原则征派徭役是一般做法。无论是一二三四五等，还是三等九则，都是赋予户一个数值级差。北宋时期出现的鼠尾册(或鼠尾簿、虎头鼠尾册、龙头蛇尾册)就是这样一种派差册籍。

王曾瑜较早对宋朝的鼠尾簿和鼠尾法进行了考证,认为鼠尾簿是以各乡的丁产簿为基础改造而成的。(13)王曾瑜：《锱铢编》，保定：河北大学出版社，2006年，第582-587页。相对五等丁产簿，鼠尾都簿最大的不同有两点，一是记录的并非全部人户，而仅是第三等以上人户；二是根据各户的物力等第(也就是各户拥有的田园、宅邸、车乘、孳畜、树木、货币，通过推排划分为若干等级)和人丁数目编排次序，在人名下记录他们历次被派给的色役的名目、年限、替换日期，将役和人一一对应起来。官员对册籍进行签署画押，将册籍留备实际派差时点检使用。而根据户部的“看详”，可知鼠尾都簿也是广义的丁产文簿之一种，编制实系“改造”文簿。没有按照“鼠尾”形式改造文簿的地方，可以采取在丁产簿内各户名下注明其“排定资次”的形式加以变通。

元明时期的鼠尾册也大致相同。和田清据《古今治平略》卷二“先丁粮多者毕，以次编其小者居后，自极大以至极小，造鼠尾册”的记载，认为鼠尾即从大到小顺序排列。(14)和田清：《明史食貨志訳註》上卷，东京：东洋文库，1957年，第243页。明万历时期，虽然解运费用已经由解运人户自理改为官府征给，但仍保留了按照册籍上户等高下佥点解运差役的形式。万历时常州府“如胖袄、茶蜡、朱漆、官布等项势不可缺者，仍用解头十九名。俱照虎头鼠尾册，田及千亩者，方为佥点”；并且详细将不同物品的解头按照负担轻重分为五等开列，如“第一等茶蜡解头一名”“事属最重”，“第五等均徭解头一名”“管解各衙门供应公费银两，事属稍轻”(15)刘广生修、唐鹤征纂：《重修常州府志》卷6，明万历四十六年刻本，第62页。注：按照后文解头人数之和为18人，似与原文19人出入。。当时的官箴书中对户等与差役轻重对应的做法也有说明。如《居官水镜》称：“概县有田人户，虎头鼠尾照数挨编，前尽北运、次南运。收头、解户，次扇书、塘长，次粮里、排年，即三尺之童，亦可据册点役。”(16)刘时俊撰：《居官水镜》卷3，明万历刻本，第14页。

此外，在帝制时代晚期，社会身份差别的影响还主要体现在对某些身份的人户表示优崇、进行赋役优免上。(17)李雪慧、高寿仙：《明代徭役优免类型概说》，《故宫学刊》2013年第2期。

第二个变化体现的是实践中制度调适的务实取向。宋代以降差役据户等而分派，评定户等自然以综合核算人丁事产最为合理，但实际调查十分困难，而又给基层胥吏诸多上下其手的作弊空间。于是牺牲理论上最理想的公平状态，而重点转为致力防弊，评定标准、手续渐趋简化，专论丁粮。(18)申斌：《明代地方官府赋役核算体系的早期发展》，《中国经济史研究》2020年第1期。

类似的做法也体现在田赋的征收方式上。比如汉代田租征收，即考虑地力差异而不考虑年景差异，以常年产量定税。在如何通过税率反映不同土地地力差异的问题上，也出现过从粗疏到细密再到粗略的否定之否定的过程。春秋时管仲在齐国“相地而衰征”，韦昭注“相，视也。衰，差也。视土地之美恶及所生出，以差征赋之轻重也”(19)如巫宝三就曾对比过劳役租制与实物租制转变时“初税亩”和“相地而衰征”，指出“相地而衰征”是按土地肥瘠不同产量分等征，而不同于“按亩数收税”，即按土地面积用同一税率征收租税(初税亩)。并且前者在租税负担公平问题上，要优于后者。巫宝三：《管仲“相地而衰征”的历史意义与理论贡献》，《经济问题与经济思想史论文集》,太原：山西经济出版社,1995年,第887页。。一般据此认为“衰征”指“据不同质量的土地制定不同的税额标准，土地质量好的多收，反之则少收”。臧知非批驳这一看法，提出“衰”字应该“不是指租税额，而是指各家实际耕种的土地数量的级差而言：在授田过程中，良田按照标准——每夫百亩授予，质量低劣的土地根据不同情况增加授田数量，加倍或者再倍，依次递增，授田民所上交的田税(租)数量是相同的。这个递增的级差就是‘相地而衰征’之‘衰’”(20)臧知非：《秦汉土地赋役制度研究》,北京：中央编译出版社,2017年,第13页。。随着田土登记制度的发展，用单位面积科则差异体现田土肥瘠的做法更加普遍。不过科则繁多也造成了易于作弊、不便核算等问题。直至明中后期实施了扒平科则等改革，很多地方通过“折亩”将不同科则的土地折算为标准土地的面积，这其实可以理解为向春秋时期以土地面积为“衰”做法的回归。

三、从衰分到鼠尾：贯彻均平理念的算学知识支撑

如果说制度设计是政治理念的直接投射，那么算学知识等技术因素中体现出的均平痕迹，则是古代政治观念向社会运作如毛细血管渗透的绝佳体现。

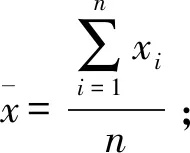
汉代《九章算术》卷三专有《衰分》一章。“衰”的意思是“差”，即差等，“衰分”本身就是有差等地分配。刘徽注说其作用是“以御贵贱廪税”，郭书春译注为“为了处理物价贵贱、赐予谷物及赋税等问题”(21)郭书春译注：《九章筭术译注》，上海：上海古籍出版社, 2009年，第97-98页。，但似较为笼统。从后面所举例题中“今有大夫、不更、簪袅、上造、公士凡五人”“欲以爵次分之”的表述，可以推知应指用来处理身份贵贱不同的人的廪和税的分配问题。今天一般将衰分直接解释为“按比例分配”问题，这其实掩盖了这一名词中“衰”所强调的差等含义。按照有差等的比例进行分配，才是衰分的完整含义。而根据差等状态不同，又涉及等差数列、等比数列等问题。(22)比如五人分五鹿问题是分配比例构成等差数列，而马牛羊食人苗问题则是分配比例构成等比数列。

为了厘清源头，我们先来分析《九章算术》关于“衰分”的记载：

各置列衰(列衰，相与率也。重叠，则可约。)副并为法，以所分乘未并者各自为实。(法集而衰别，数本一也，今以所分乘上别，以下集除之，一乘一除适足相消。故所分犹存，且各应率而别也。于今有术，列衰各为所求率，副并为所有率，所分为所有数。又以经分言之，假令甲家三人，乙家二人，丙家一人，并六人，共分十二，为人得二也。欲复作逐家者，则当列置人数，以一人所得乘之。今此术先乘而后除也。)实如法而一。不满法者，以法命之。

关于该算法的数学含义，据相关研究转述如下。(23)曲安京主编：《中国古代科学技术史纲·数学卷》，沈阳：辽宁教育出版社, 2000年，第200-201页。

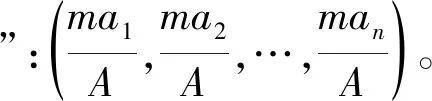
假设有n个人分配m个物，那么先列出每个人的列衰(即分配比例(24)郭书春译注：《九章筭术译注》，第97页。)a1，a2，…，an(25)如果其中有多个人的列衰(ai)相同，可以合并开列，以人数乘以列衰。，将全部列衰相加，即a1+a2+…an=A，将所得之和(A)作为“法”，在运算上表现为乘数或除数。(26)“实”指的是实在的事物数量，“法”指的是衡量事物的单位。表现在运算上，实就是被乘数或被除数，法就是乘数或除数。然后用“所分”(m)与“未并者”(a1，a2，…，an)分别相乘，得出各自的“实”，也就是被除数。每个人的“实”除以“法”得到的就是每个人应得的物的量。

现代数学中谈到某个个体的分配比例时，一般用分数表示个体在总体中所占份额，其和为1。但是在这里，列衰指的是体现个体与个体之间“差等”的比例关系，而且这种比例关系往往是以具体数字的形式出现的。比如“衰分”所举的第一个例题“今有大夫、不更、簪袅、上造、公士凡五人，共猎得五鹿，欲以爵次分之”，这里说的就是大夫、不更、簪袅、上造、公士的分配结果应呈5∶4∶3∶2∶1的比例关系。

我们认为，宋代以后的“鼠尾”的算法规则，正是与上述“衰分”的差等内在原理相同，这在不同时代的算学书中呈现着类似的例证关系。前人研究鼠尾问题时并未重视该问题，大致是由于传世经典文献记载阙如。

重新探讨该思路最重要的文本是新发现的成书于明正德、嘉靖间的《新集通证古今算学宝鉴》(以下简称《算学宝鉴》)。作者王文素，字尚彬，山西汾阳人，明成化年间随父王林经商并定居河北饶阳。该书唯一传世的抄本存于国家图书馆，系20世纪30年代由国立北平图书馆人员于旧书肆中发现。据前人研究，该书除引用参考过较多的宋元算经外，其中还有不少原籍早已亡佚的明代算经。该书于1993年影印出版，虽曾受数学史学者瞩目，但尚无学者关注其特殊的经济史料价值。(27)王文素著、刘五然等校注：《算学宝鉴校注》，北京：科学出版社，2008年。《精明算法》撰者不详。关于《算学宝鉴》征引宋元明算书情况，参见李俨：《中算史论丛》第2集,北京：中国科学院,1954年，第90页；赵擎寰：《明王文素〈算学宝鉴〉浅析》，《珠算》1998年第3期。

《算学宝鉴》在书首的提要中就明言“贵贱易交凭粟米，公私科派用衰分”(28)王文素著、刘五然等校注：《算学宝鉴校注》，第11页。。又在第二十三卷中提到《精明算法》中有“五人鼠尾均钱”的问题，认为其解法即南宋杨辉的《续古摘奇算法》所阐释的《九章算术·衰分》第一问的解法。这说明所谓“鼠尾均”即“衰分”。值得注意的是《九章算术·衰分》第一问原文表述是“欲以爵次分之”，但杨辉《续古摘奇算法》中的表述是“五人均五鹿”，《精明算法》也有“鼠尾均”的表述。这说明至少从宋代开始，算学中的“均”并非意味着平均分配，而是按照有差等的比例分配。

那么何为“鼠尾均”呢？《算学宝鉴》校注者一方面指出“鼠尾差分”相当于现在的等差数列，另一方面又引《宋史·赵开传》为书证，将“鼠尾”解释为“从头至尾，一一顺次排列”，这大约受了传统史学界对鼠尾法解释的影响。仔细分析《算学宝鉴》中有关“鼠尾”的算例，可以发现“鼠尾”并非作为名词，而是用作副词，修饰后面的“差分”“均”“分”等动词。比如“众人鼠尾分钱，且云首多尾十六文，递差四文。问：总人几名？”“假令二十五人，鼠尾均银十两，务要首出银五钱五分。问：尾出银及递差几何？”“假令三十三人鼠尾均银十三两二钱，但知尾出一钱六分。问：首出并递差几何？”“七人鼠尾均银十两，且云甲出二两。问：乙、丙、丁、戊、己、庚并递差各该几何？”“假令十人鼠尾分银十两,只云甲多癸一两八钱。各该几何？”“假令八人鼠尾分银七两二钱，欲令下五人得上三人七分之五。问：各该几何？”(29)王文素著、刘五然等校注：《算学宝鉴校注》，第9、291、282、284-285、289页。等等。从这些算例的解答中，就可以看出“鼠尾”一词本身包含着比例系数呈“递差”变化的意思。

王文素在“鼠尾差分”部分认为《九章算术》的“衰分”第一问的计算方法(也就是设定的分配比例构成了公差为1的等差数列)过于简单，无法处理复杂的问题，他说：“假令万人均钱，岂可以首出尾之万倍哉！”故此设计出新的方法，“庶补衰分之万一”。他在“双鼠尾差分”部分批评《九章算术》“求衰之法未通”，“遇此人数差一分、物数相等者可矣，或人数差多分、物不等者不能求之”(30)王文素著、刘五然等校注：《算学宝鉴校注》，第288页。。

所以，“鼠尾”是一种特殊的“衰分”计算方法，分配比例构成等差数列，符合an=a1+(n-1)×d，其中an即“衰”，d就是递差之数。而且，从《算学宝鉴》午本提要“鼠尾使富贫不怨”(31)王文素著、刘五然等校注：《算学宝鉴校注》，第11页。可以知道，这一算法大概是与赋役均平目标相关。

由以上分析以及对照“衰分”的定义可知：“鼠尾”的含义即为an，an-1，…，a2，a1，n为项数，总和为Sn，公差为d的等差数列。易见若只给出n和Sn，则各项数的解并不唯一。这一点王文素在“五人鼠尾递差均钱六百文”的例子中也有提及，在原有的(200，160，120，80，40)的古人解之外，他又另外给出了(144，132，120，108，96)、(140，130，120，110，100)、(150，135，120，105，90)三组解，指出“解曰：前一答述古所云，后三答是愚所续。尝论此术，题内若无定则拘之，只云递差在，岂止四答而已”。

书中有大量与“鼠尾”有关的例子，其中“口诀”即为运算方法，“问”即为例子。鼠尾差分来自该书第二十三卷，其中共包含鼠尾差分七口诀(32)即首尾求衰口诀、鼠尾求差求积求人总诀、首尾差求首尾口诀、首尾互求、差求首尾、首尾求差(两首)。二十一问，双鼠尾差分二口诀(双鼠尾差分求衰口诀、双分口诀)四问。王文素的歌诀中有关级数的校验过程，可详见潘丽红、潘有发之文(33)潘红丽、潘有发：《王文素的级数论》，李迪主编：《数学史研究》第7辑，呼和浩特：内蒙古大学出版社、台北：九章出版社，2001年，第59页。，因本文篇幅和主题所限，不再赘录推证过程。该文验证了《算学宝鉴》中相关章节的口诀均正确。如“鼠尾求差求积求人总诀”为：

首尾差求次递差，总人去一便除他。(1)

尾头差要求人数，次递差除一个加。(2)

首尾并乘求总积，总人乘折见根芽。(3)

算中多用斯三者，法理通玄实可夸。(34)王文素著、刘五然等校注：《算学宝鉴校注》，第282页。

此外，在具体在算法方面，有以下解释：如“比证新题”中，假令八人鼠尾分银七两二钱，欲令下五人得上三人七分之五。问：各该几何？甲一两六钱，乙一两四钱，丙一两二钱，丁一两，戊八钱，己六钱，庚四钱，辛二钱。有关此例有以下两点说明：

其一，“鼠尾分银”也如上所述，为“鼠尾”+“分”的形式，说明这里动词“分”是按照“从大到小排序，且依等差数列减少”。从王文素的算例解答可以看出，这样的排序方法为(以两为单位)：1.6、1.4、1.2、1、0.8、0.6、 0.4、0.2。这里在鼠尾排序后，自然生成了“上”“下”的大小关系，“上三人”指甲、乙、丙，之和为4.2，“下五人”指丁、戊、己、庚、辛，之和为3，而3÷4.2=5/7符合题意。可见鼠尾的排序规则为上大下小，并且解是唯一的。

其二，在该类算法的求解过程中，存在所谓“双鼠尾”的情形，意为分左右两列进行排序(“双双鼠尾递差均”)：

千字文鼠尾均银一千两，欲令下六百字出上四百字七十七分之四十八。问：上四百首尾二字并下六百首尾二字各该几何？答曰：天字一两八钱九分九厘一毫，移字一两一钱八分零九毫，坚字一两一钱七分九厘一毫，也字一钱零九毫。(35)王文素著、刘五然等校注：《算学宝鉴校注》，第290页。

原稿中术文算法比较烦琐，并列出了“求衰法”和“双分法”两种解法，结果完全相同。可见“鼠尾均银”本身就是属于传统古算中“衰分”算法的一种，只是后者比前者简捷。对此王文素认为“观此二法，双分为简，立衰为繁。亦不可不传，苟或不传，则无以见求衰之妙。故并存之，以晓初学”。双分口诀如下：“双分鼠尾递差均，各另除银寄位存。以少减多余剩数，总人除出半差真。上人去一相乘了，并上除银是甲银。全差减甲余为乙，递减全差往下寻。”(36)王文素著、刘五然等校注：《算学宝鉴校注》，第288页。

根据原稿算法排列格式，因排版原因，我们梳理简化其计算过程如图1所示：

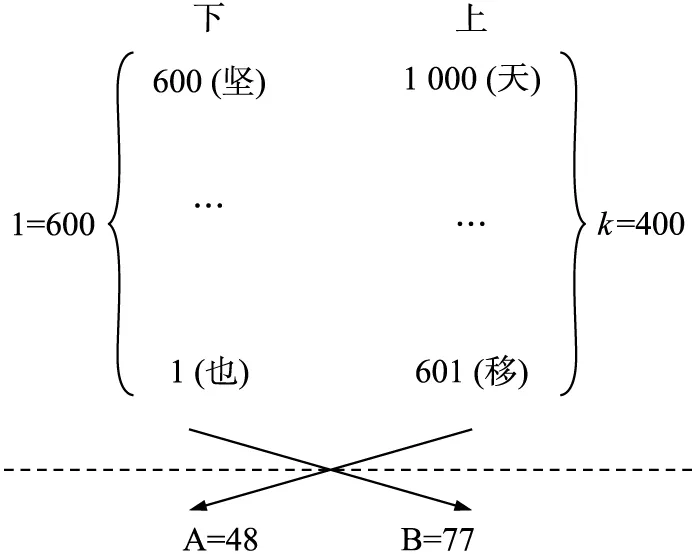
图1 《算学宝鉴》千字文鼠尾均银计算简图

按照口诀术文所示，其中“天”“移”“坚”“也”均为千字文排序字码。计算公式如下(具体推导参见前述潘红丽、潘有发之文)：

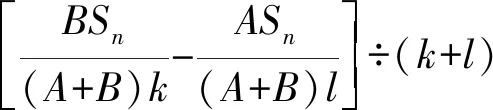
四、从“鼠尾”到“均平”：分配系数与相对公平的实现

明代的算书中，出现了直接以“均平”为名的问题，通过衰分法来解决。笔者管见所及，在明代以前的算书中，尚未发现有以“均平”来命名一类应用问题的，而在明末清初之后，“均平”被作为一类问题普遍收入算书之中。这或许与赋役改革中摊派计算的扩大引起新的计算需求有关。

这一词语首先出现在万历二十年(1592年)程大位的《算法统宗》中。该书卷五《衰分章》开篇解释说：“衰者，等也。物之混者，求其等而分之，以物之多寡，求之出税；以人户之等第，求之差徭；以物价求贵贱高低者也。”(37)程大位著、梅荣照、李兆华校释：《算法统宗校释》，合肥：安徽教育出版社，1990年，第371页。要把混杂在一起的人户划分等次，课征不同的差役。而衰分计算的目的，如紧接着说明计算方法的《衰分歌》末句所言，“以乘各数自均平”，在于实现“均平”。

随着赋役定额化的发展，摊派计算更加普遍，成为基层赋役计算的必要技术。《衰分章》有如下例题：“今有官米七十三石二斗，令三等人户出之。上等二十五户，每户五分，中等四十户，每户三分，下等六十户，每户一分，问各等户米若干。”这显然是一个在里甲范围内，对税粮负担进行摊派计算的场景。例题“今有官田一顷三十八亩，每亩科正米二斗。今要七分本色，三分折纳细丝。每米一石，折丝一斤。问各纳若干”，则体现了田赋不同征纳物之间的比例划分。而且摊派计算不局限于田赋领域。在“三七差分”下的另一个例题更是明确落实在徽州地方场景上：“今有金三千两，令休绩二县金行铺户三七上纳，问各该若干。”(38)程大位著、梅荣照、李兆华校释：《算法统宗校释》，第377、379、387页。

此外，衰分计算此时在赋役运作上还有了新的用武之地。到万历中期，各项赋役已经普遍折银征收，但是解纳时不少项目仍须纳实物，于是地方官府需要用征来的银子买本色上纳。(39)申斌：《清初田赋科则中本色米复归的新解释——兼论明清赋役全书性质的转变》，《中国经济史研究》2019年第1期。在“总收分解”的制度下，不同税目折银后统一征收，购买时却需要分别支付。由于物价变动等诸多原因，购买解纳实物所需价银和账面上这些物品的折银额并不一致，于是需要根据所征总银额和不同物品的时价，以及所需解纳物品的数量要求，来计算购买经费的分配方案。《衰分章》的第一个例题就与此有关：“今有银一千二百两，买绫绢，议要绢一停，绫一停，其绫每匹价三两六钱，绢每匹价二两四钱。问二色并价各若干。”《贵贱差分歌》解决的也是知道甲、乙的单价，知道共价买共物若干，求甲乙各几何的问题。《算法统宗》卷九《均输》，更是明确地把用衰分法来解决的此类问题称作“均平”问题。是章卷首解题“均输”说“均平也，输送也。此章以户数多寡、道里远近而求车数粟数，以粟数高下而求僦直，以钱数多少而求而佣钱”。其方法是根据题目条件，求得定率，然后施以衰分术。(40)程大位著、梅荣照、李兆华校释：《算法统宗校释》，第372、643、665页。该卷第一道例题为“今有银二十二两八钱买黄白蜡，各要均平。其黄蜡每三斤价银四钱，白蜡每斤价银五钱。问黄白蜡各若干”。万历四十一年(1613年)译成的《同文算指》也收录此问题：

问以银二十二两八钱买黄白蜡均平。其黄蜡每三斤价四钱，白蜡每一斤价五钱。二色之价名若于此，以两母子互乘(三五一十五，一一四如四)，并得一十九为首，率两毋相乘为次率，总银为三率，求得二色各斤数。

一、一两九钱；二、三斤；三、二十二两八钱；四、三十六斤(以乘白蜡得一十八两，以乘黄蜡，三除之得四两八钱)。(41)李之藻撰：《同文算指通编》卷1，清道光二十五年至咸丰元年番禺潘氏刻光绪十一年增刻汇印海山仙馆丛书本，第36-37页。

此类算题，在之前的古算书中出现过，但多为“均分”项，并无明确的“均平”一词概念的出现。按字面理解，实际均平可能是按“银”均平，也可能是按“物”均平。该算题实质是将银通过本色物料单价，直接转化为求本色物料的重量平均，即“均平”的意思并非按银价平分，而是按“物”。

此类计算相当于涉及物料加权分配，即征本色黄蜡重X1斤，本色白蜡重X2斤，

由于“物料”均平，则X1=X2，解之得X1=X2=36。可见是以36斤重量均分本色黄蜡白蜡，使总价为22.8两。

此类的“均平”也并非仅指两两平均，《同文算指》也列举了三种类型的物料均平计算例子：

问官银一万七百七十八两六钱五厘，籴米、麦、豆三色均平。其每一石价米二两三钱五分，麦一两九钱五分，豆一两四钱五分，各价几何？各石几何？

并三价共五两七钱五分为法，置第一率。总银为第二率。列三色每石价为第三率。推得第四率。是各价数、其各石数以法径除总银，即得：

一、五两七钱五分；二、一万零七百七十八两六钱〇五厘；三、二两三钱五分、一两九钱五分、一两四钱五分；四、四千四百〇五两、三千六百五十五两、二千七百一十八[两](42)按原式计算后米麦豆三者分配两分别为4 405.187两,3 655.368两和2 718.094两，原文省略了两以下小数。。一钱六分九厘(米)，三钱五分三厘(麦)，两〇八分三厘(豆)。三色共一千八百七十四石五斗四升。(43)李之藻撰：《同文算指通编》卷3，第9-11页。

设米X1石，麦X2石，豆X3石，按题意有：

由于三者物料均平，则X1=X2=X3，解之即得X1=X2=X3=1 874.54石(44)原式计算结果为1 874.547826石，按原文省略升以后小数。。其中计算原理即以2.35、1.95、1.45每石价银求和为5.75两每石作除数，来除总官银数目。计算过程中出现的第一率、第二率、第三率、第四率即术文中提到的“一、二、三、四”后的数字。

入清以后，这一类算法也见于算书例题。如清初《新纂简捷易明算法》中有以下例题：

假如有银六十两，贾黄白蜡各要均平，其黄蜡每三斤价银四钱，白蜡每六斤价银一两六钱，问黄白蜡并价各该若干？

答曰：各该一百五十斤。(黄、白)蜡价银(二十两、四十两)。法将黄蜡三斤为法，以价四钱为实归之，得每斤价银一钱二分三厘三毫三丝三忽三微三尘三渺三漠三埃三纤三沙，又将白蜡六斤为法，以价一两六钱为实归之，得每斤价银两钱六分六厘六毫六丝六忽六微六尘六渺六漠六埃六纤六沙，二共并得四钱为法，以总银六十两为实归之，各得各该一百五十斤，各以价银乘之，得数合问。(45)沈士桂：《新纂简捷易明算法》卷3，清刻本，第33-34页。

此类计算相当于涉及物料加权分配，即征本色黄蜡重X1斤，本色白蜡重X2斤，

由于“物料”均平，则X1=X2，解之得X1=X2=150斤。

可见计算均平时，所需参数仅需总共分配本色重量以及各色物料之单价即足够，计算过程并不复杂。这些主要划归礼部的本、折色药材，在各项名目下种类繁多。物料的均平分配计算有利于在保证总分配银两额定的情况下，根据权重不同，分配物料称重相等或为整数，这样可能便于实物征收时的核对和统计。

五、民间赋税分担中的算学知识运用

按比例分配如果是一种合理的“均平”方案，那么其使用范围也就自然不局限于官府的制度设计，也会体现于民间实践当中。《算学宝鉴》“攒纳差分”就留下了一个例子，这可以认为是在已知“衰”的情况下，计算实际分配数值。“攒纳差分置正粮，并之为法寄于傍。攒粮另并观多少，多则开除少并详。各与正粮乘作实，正粮总数法除强。除来各与攒粮较，谁少谁多见短长。”(46)王文素著、刘五然等校注：《算学宝鉴校注》，第297页。文中有四类计算题目，并配有具体解法，笔者将如下例题汇入表1(见下页)中，单位全部按照“斗—升—合”十进制单位换算成阿拉伯小数，以便简化条件和问题的数据，参见“1.适足题”正文如下：

适足题：甲该正粮一石五斗，原攒一石八斗；乙该正粮九斗，原攒一石一斗；丙该正粮六斗，原攒七斗。混运赴仓，交纳适足。问：三人孰多孰少？答曰：甲适足，丙贴乙二升。(47)王文素著、刘五然等校注：《算学宝鉴校注》，第297-298页。

四类题目如下页表1所示。明代赋税史料中常见的“正粮”与实际纳粮户的负担不同，它是一个法定应缴税额，为实际税负的摊派基准，据此可计算出按比例分配的比率。(48)申斌：《明代地方官府赋役核算体系的早期发展》，《中国经济史研究》2020年第1期。上面例题中的“正粮”正是扮演这种角色。

同一仓口的粮额由几个纳粮户共同来缴纳，上述例题中，三户正粮总额均为3石，三户攒粮(凑集的粮食)总额均为3.6石。再结合“适足”“余剩”“不足”的表述，三题中向各仓纳粮实际所需粮额分别为3.6石、3.4石、3.74石，均超过正粮额。这一情况可能是附加性征收造成的，也可能是运输中的损耗和上纳中应对各种盘剥造成的。总之，这些数额才是对粮户而言的真实税负支出。而且这一真实负担支出，在完成缴纳之前往往是不确定的，所以我们才会看到三户各自凑集粮食，一起混运上仓完纳后，出现既可能有余剩，也可能不足的情形。由于实际总支出不确定，那么三户为了完成这次缴纳任务究竟需要准备多少粮食也就无法事前预知，所谓“攒粮”只是各户预先凑集准备的粮食。只有等完成缴纳后才能根据实际支出总额，来详细计算各自应该负担的支出。这些例题所展示的正是完纳税粮后，纳粮户之间计算各自应负担支出及彼此债务关系的过程。

那么如何在承担同一仓口缴纳任务的三户间分配实际税负？解决方案就是依照三户各自正粮额比例分摊。如适足题中，按照“正粮”比例，三人所凑总额虽与实际总支出相符，但按照正粮比例，乙应分摊出办1.08石，而攒粮时多出0.02石，丙则比应分摊出办的0.72石少出0.02 石，故此形成了需要“丙贴乙两升”的债务关系。余剩题、不足题处理的则分别是事前凑集(攒粮)总额多于、少于实际支出情况下，各自取回、添补数额的划分问题。这一例题说明了在民间赋税分担实践中，不但同样贯彻了以各户税粮额为基准、按照比例分配税负的“均平”原则，而且灵活运用了“求衰”相关的算学知识。

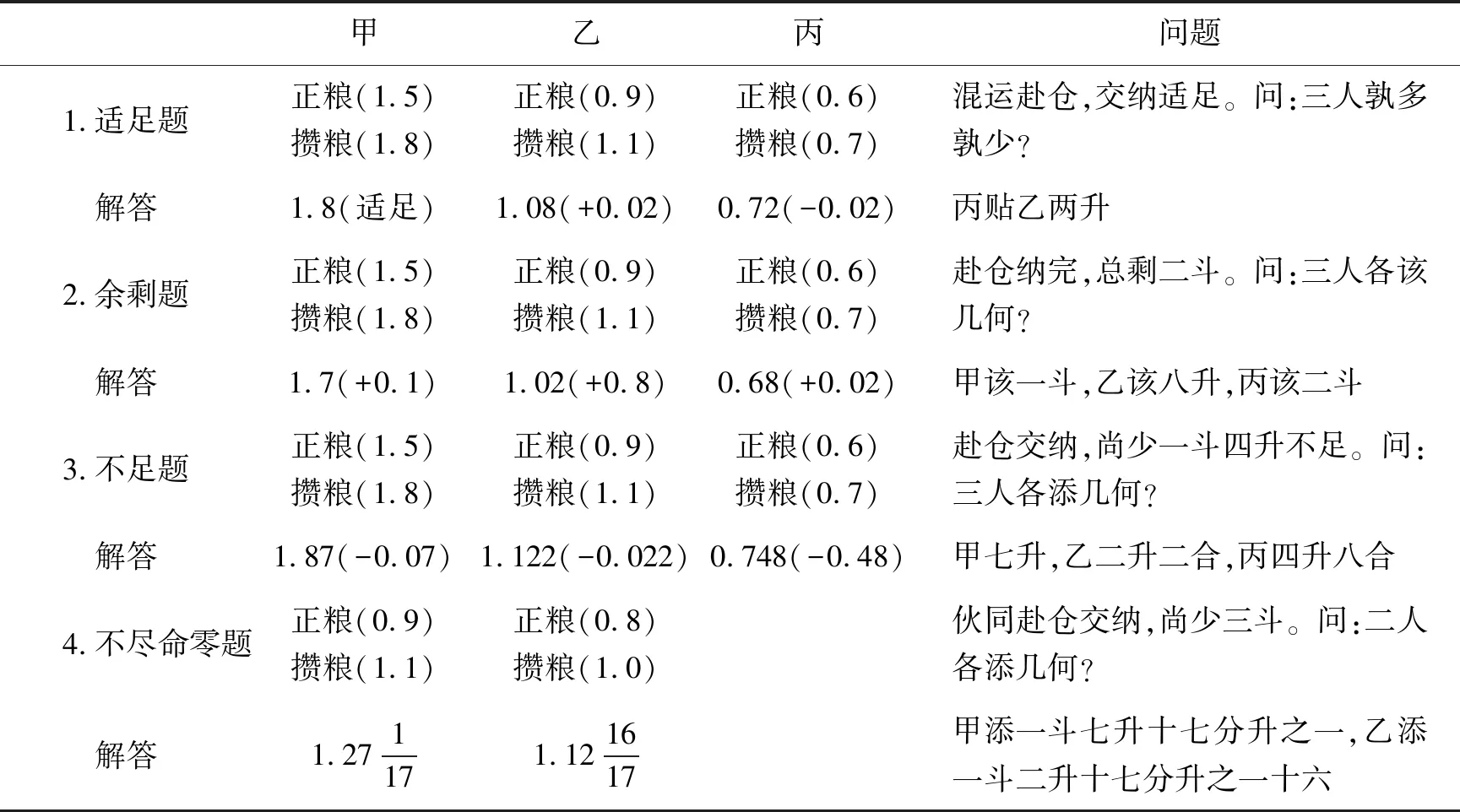
表1 《算学宝鉴》“攒纳差分”分类例题

结 语

本文以“均平”为切入点，透视传统中国赋役运转领域的理念、制度与技术，阐发其内在关联和一致性，开拓中国古代制度史研究的一个新路径。以差等为前提的“均平”观念，作为中国本土的公平价值和正义观，体现在土地、赋役等经济分配和财政汲取制度各个环节。古算书中赋役相关的算例揭示了概念虽有“衰分”“鼠尾”“均平”等多种表述，但其实质内涵都是依照不同的比例系数(权重)分配财、物、役、钱，体现了均平合理性观念。如果说纯粹的国家或儒家理念只能依靠教化来推行，那么渗透于算学这类技术性知识中的理念因素，则随着实践性知识而被民间广泛采用，润物细无声地沉淀到民众的头脑中，形塑着对“平等”的文化认知。从社会性技术的层面来解读中国传统文化理念，当是制度史和思想文化史交融共进的重要理路。