一种分布式发电功率时间序列波动性量化评估方法

陈 晨 袁绍军 尹兆磊* 贺晓红 杨慢慢 李润鑫

①(国网冀北电力有限公司承德供电公司 承德 067000)

②(华北电力大学能源动力与机械工程学院 保定 071066)

1 引言

随着传统化石能源的逐渐消耗以及人们对环境保护的重视，可再生新能源已成为替代传统高碳排放发电方式的必然趋势。为有效应对能源危机与环境污染问题，我国提出了“碳达峰”和“碳中和”的伟大目标。只有不断发展分布式发电技术，不断提高风力发电、光伏发电等可再生能源在电网的渗透率，我国电力系统才能逐渐变得越来越清洁、高效[1,2]。因此，大力发展分布式发电技术，提升可再生能源的渗透率是实现“双碳”目标的必经之路。

当前，分布式可再生能源以风力发电和光伏发电规模最大，发展最为成熟。然而，由于风、光本征的不确定性，风力发电和光伏发电的功率具有很强的间歇性和波动性。风力发电和光伏发电的这种固有特性使得电力系统的安全稳定运行受到严重威胁[3–5]。因此，人们期望通过一些手段认识分布式发电功率的波动特性，进而提出有效的方法应对波动性给电力系统带来的问题。目前，采用数理统计的方法研究风电、光伏等分布式发电功率的概率分布模型是当前常用的分析手段[6–8]。然而，这种定性分析方式只能把握分布式发电功率的统计分布特征，并不能对波动性进行定量的解释[9–11]。此外，对分布式发电输出功率进行预测，进而指导系统调度，降低波动性带来的风险也是一种常规的降低波动性引发问题的方式[12,13]。然而，现有预测方法往往难以获得令人满意的预测效果。此外，多数预测方法的普适性很差[14]。

实际上，若能定量地认识分布式发电功率的波动特性，不但能够促进对不同分布式发电方式的认识，更有利于根据分布式发电功率波动性充分发掘需求侧闲置的柔性资源，进而提升新能源的消纳能力。此外，定量地认识分布式发电功率的波动特性还有助于帮助建立更好的功率预测模型。因此，对分布式发电功率序列的波动性进行准确的定量刻画具有十分重要的现实意义。

然而，分布式发电功率波动特性定量分析方面的研究较少，早期方法仅仅采用一些常规的统计量对分布式发电功率的波动性进行评价，如采用均值、方差等[15,16]。然而，这种评价方式仅仅能够反映时间序列总体情况的统计特征，并不能用于比较任意两个分布式发电功率时间序列的大小。基于此，文献[17]提出了采样损失率的概念来刻画风电功率的波动性。文中利用波动性不同的时间序列在相同采样周期下获得的采样序列损失信息的不同来衡量波动性。类似地，文献[18]定义了信息损失率的概念来刻画风电功率的波动性。文中先将风电功率进行滤波使之变得平滑，再将平滑后的风电功率序列和原序列间的差异作为评价其波动性的指标。两种方法的思路类似，都在一定程度上实现了对风电功率波动性的有效定量刻画。但是，两种方法本质上都只考虑了风电功率时间序列的高频信息(即如时间序列上的“毛刺”，类似于噪声)中的波动成分，忽略了低频信息(即时间序列的变化趋势，去掉“毛刺”后的相对平滑的时间序列)中波动幅度对波动性的贡献。

基于此，为获得性能更好的分布式发电功率波动性刻画方法，本文提出了一种新方法和新指标。首先利用上下包络和勒贝格积分定义了波动面积比来刻画高频信息中的波动成分。然后，利用相等时间窗内包络线中值线的幅值差，定义了波动幅值比，用于刻画变化趋势中的波动成分。最后综合定义了波动性衡量指标——波动率。该方法并不需要对分布式发电功率曲线进行平滑处理等额外操作，充分考虑了分布式发电功率的高频波动和变化趋势波动，获得的指标能更全面地反映分布式发电功率的波动性。

2 典型时间序列的直观分析

文献[17]和文献[18]在建立风电功率波动性定量刻画指标时，本质上都只考虑了风电功率时间序列的高频信息中所包含的波动信息。实际上，分布式发电功率时间序列的波动性应由高频波动性(高频信息中的波动性)和变化趋势波动性(低频信息中的波动性)两部分构成。在定义分布式发电功率波动性指标时仅仅考虑高频波动性是不全面的。不同于现有方法，观察到波动性越剧烈的时间序列，其上下包络线[19,20]内的面积越大这一直观认识，本文首先尝试利用该面积来定义分布式发电功率时间序列的高频波动性。

如图1所示，分别考察相同时间长度(时间长度为200 min，间隔为1 min)的直线y=0.1x+10、小波动时间序列和较大波动时间序列(最大幅值为49.5)。从图中可以看出，波动越剧烈的时间序列，包络线内的面积相对越大。

图1 不同时间序列及其上下包络线

此外，从图1还可以看出，除包络线内面积不同外，图1(b)中时间序列的变化趋势也较图1(c)中的时间序列更平缓，图1(c)中的时间序列变化趋势上下波动的幅度更明显。倘若在某些特殊情况下，图1(c)中的时间序列的曲线变得平滑，有可能出现其包络线内面积比图1(b)中包络线内面积更小的可能。而且，如图1(c)所示，黑色椭圆中的面积几乎为0，而此部分恰恰是分布式发电功率曲线中波动性剧烈的时间段，这种波动性并不能反映在高频信息中。因此，仅仅考虑分布式发电功率曲线的高频波动性是有失偏颇的。值得注意的是，这一缺点同样是文献[17]和文献[18]中方法的缺点之一。

基于上述直观分析，在建立分布式发电功率波动性定量刻画指标时，应同时考虑分布式发电功率时间序列中高频信息和低频信息中的波动性。基于此，本文借助时间序列的包络线和勒贝格积分理论，考虑固定时间窗内时间序列的幅值变化，定义了全新的衡量分布式发电功率时间序列的波动性指标。

3 分布式发电功率波动性定量刻画方法

3.1 衡量高频波动性的指标定义

3.1.1 包络线的定义

首先定义分布式发电功率时间序列上下包络线，用于求取高频信息的波动面积。

定义时间长度为T的分布式发电功率时间序列为x(t) ，t∈{t0,t1,...,tN}，T=tN −t0。

将该时间序列划分成长度为l的等长子区间[ti−1,ti](i=1,2,...,N)，定义为时间窗，其中N为时间窗的个数N=「T/l⏋；

然后，分别求取各个时间窗[ti−1,ti]内时间序列的最大值xmax(tk)和 最小值xmin(tk)，tk ∈[ti−1,ti]；

之后，利用线性插值方法将最大值和最小值序列插值成长度为T 的时间序列(t)和(t)，t ∈{t0,t1,...,tN}，分别作为分布式发电功率时间序列的上下包络线；

最后，定义上下包络线的面积为时间窗长度为l的波动面积，记为Sl。

注意到上下包络线与分布式发电功率时间序列一样均为离散的时间序列，因此求取波动面积时不能采用黎曼积分理论，因为离散时间序列不具备黎曼可积条件。所以，本文将借助勒贝格积分理论对该面积进行求解。

值得一提的是，波动面积的大小与子区间长度l的选取有关。随着l的增大，波动面积会呈现出增大的趋势。当l=1时，求取的上下包络线与原时间序列一致，则Sl=0 。因此，本文假设l>1。另外，对于无波动的时间序列(直线)，无论l取为何值，都有Sl=0。

3.1.2 勒贝格积分

勒贝格积分(L-积分)不同于黎曼积分[21]，其相比于黎曼积分而言扩大了可积函数的范围，使得很多非常不连续的函数也具备可积条件。因此，对于间断点积分问题，是不可多得的理论工具。

L-积分的定义为：如果函数f(x)为可测集E区间[a,b]上 的有界可测函数。设f(x)的上界和下界分别为Fm=inf{f(x)},FM=sup{f(x)}。将上下界构成的区间[Fm,FM]划 分成n个子区间[sk,sk+1]，其中k={0,1,...,n −1}， 记s0=Fm，sn=FM，Ek={x|sk ≤f(x)≤sk+1,x ∈E}。 那么，每个Ek均为可测集。

定义Ek的大和Mmax(t) 、小和Mmin(t)分别为：

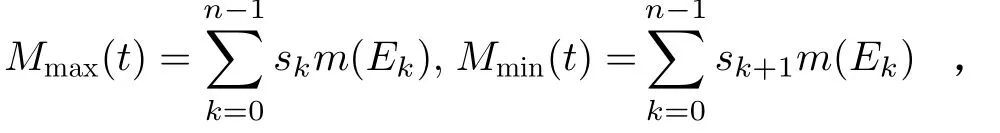
其中，m(Ek)为Ek的测度。那么，对于有界可测函数f(x) ， 必然有I==，勒贝格定义I为有界可测函数f(x)在可测区间E上的L-积分，记作

3.1.3 波动面积比的定义

定义波动面积为上下包络线之间的面积，可利用L-积分进行求取。则子区间长度为l的波动面积为

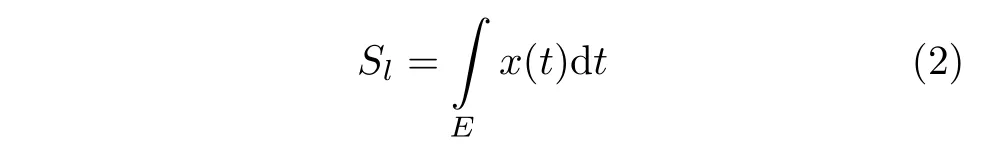
然后采用装机容量和时间序列长度对定义的波动面积进行归一化处理，作为刻画分布式发电功率高频波动性的指标——波动面积比为

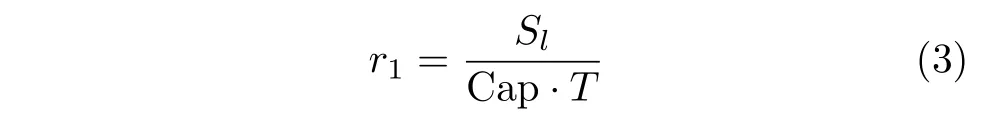
其中，Cap为分布式发电功率的装机容量，T为时间长度。

由定义式(3)可知，r1相当于分布式发电功率时间序列在时间长度T内上下包络线内的面积与分布式发电满发功率下在时间长度T内总面积的比值。这种定义方式可以消除不同时间长度和不同装机容量的差异，使得指标可以比较任意两个分布式发电功率波动性的大小。

3.2 衡量变化趋势波动性的指标定义

3.2.1 分布式发电功率时间序列趋势定义

分布式发电功率时间序列的变化趋势可以由去掉高频信息(“毛刺”)的分布式发电功率曲线来反映。该趋势可以利用如文献[18]中所述的滤波方法获得。如图1所示，观察到时间序列的上下包络线的中值线在一定程度上能反映出分布式发电功率时间序列的变化趋势，为简单起见，本文采用分布式发电时间序列上下包络线的中值线反映其趋势，中值线的定义为

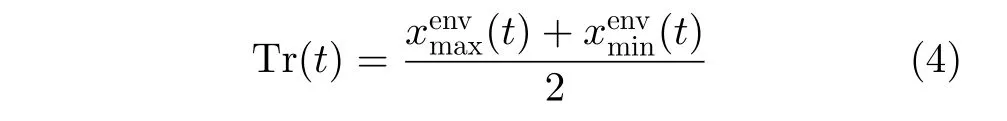
3.2.2 波动幅值比定义

为定量刻画分布式发电功率低频信息中的波动性，尤其是反映图1(c)中黑色椭圆中包含的波动信息，本文采用固定时间窗内中值线幅值的均值与装机容量的比值来刻画波动性的大小，命名为幅值比，其定义为

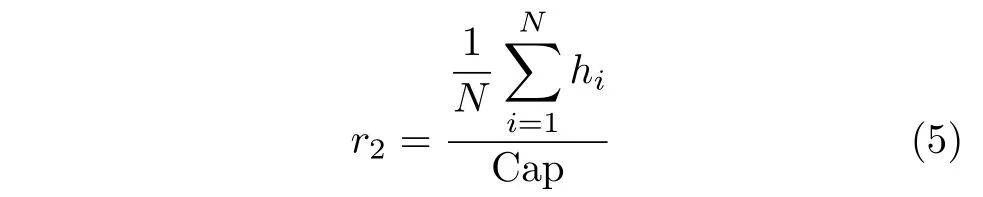
其中，hi=max{Tr(t)}−min{Tr(t)}，t∈[ti−1,ti]，N为时间窗的总数，Cap为装机容量。

需要说明的是，这里时间窗的长度的选择可与求取包络线的时间窗相同，亦可不同。为简单起见，本文采用与求取包络线时相同长度的时间窗。

3.3 波动率的定义

综合波动面积比和波动幅值比，将高频信息中的波动和低频信息中的波动同等看待，定义用于衡量分布式发电功率波动性的指标—波动率如下：

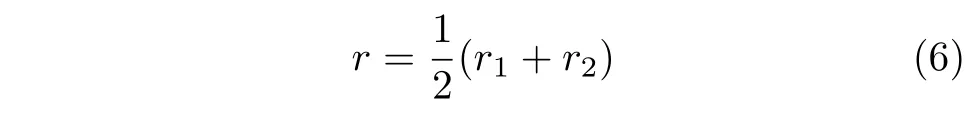
该波动率在定量刻画分布式发电功率的波动性时具有如下优点：

(1)波动率r在定义时充分考虑了分布式发电功率中的高频信息和低频信息中的波动性，能更全面、准确地反映分布式发电功率的波动性。

(2)波动率r可以比较不同装机容量和时间长度的分布式发电功率时间序列的波动性。

(3)波动率r的定义更加直观，求取过程简单。为认识分布式发电功率波动性提供了新的视角。

值得一提的是，本文所提出的波动性衡量指标是根据时间序列的特征设计的，理论上可以用于衡量任意时间序列的波动性。

4 算例分析

为验证定义的波动率r在衡量分布式发电功率波动性的有效性，本文利用典型的具有较强随机性和间歇性的风电功率时间序列进行验证分析。首先验证直观上波动性不同的风电功率时间序列的波动率r；然后验证波动率r是否能够准确反映风电功率的平滑效应；之后验证波动率r能否反映不同时间长度和装机容量下的风电功率时间序列；最后利用特殊时间序列，通过对比文献[17]、文献[18]以及文献[19]中的波动性指标，验证本文定义的波动率r的有效性和优越性。

本文仿真实验的数据来源为我国北部某风电场的实测数据，该风力机总数为132台，单机额定容量为1.5 MW，总装机容量为198 MW。风电功率时间序列的采样时间间隔为15 min，总采样时长为43200 min(30 d)。

4.1 直观上波动不同的风电功率时间序列的波动率r

图2给出了直观上波动性较小和波动性较大的风电功率时间序列a和b(一期33台风力机，总装机49.5 MW，总时间长度为3000 min，即200个采样点)。在本实验中，选择l=10。

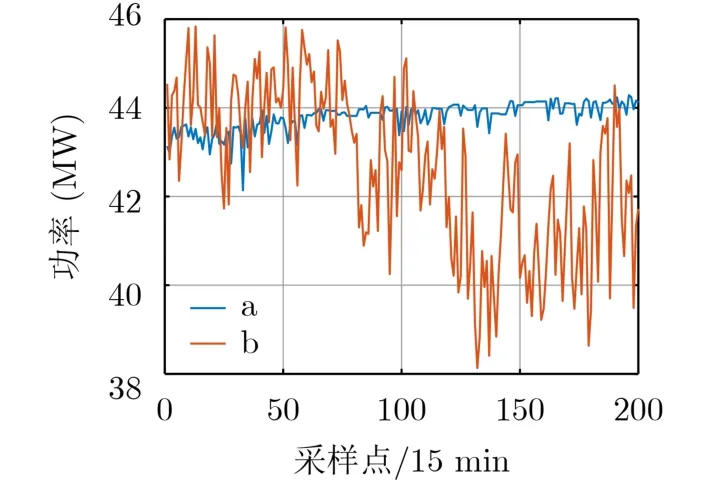
图2 波动性不同的风电功率时间序列

由于预测准确率能在一定程度上反映风电功率时间序列的波动性大小，因此本文采用风电功率预测结果来对比所提出的波动性指标，以验证波动率r在面对不同波动性的风电功率时间序列的有效性。此外，本文还将所提出的波动性指标与文献[17]、文献[18]以及文献[19]中提出的波动性衡量指标进行对比，这些指标都具有时间序列波动性越大，指标值越大的特点。

本部分实验采用的预测方法为持续法[22]和自回归滑动平均法(ARMA)[23]，方法的预测准确性用均方根误差来衡量，其定义为

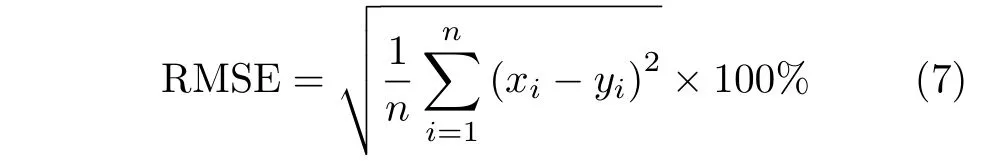
表1给出了风电功率时间序列a和b的不同波动性衡量指标值和功率预测的结果。从表中可知，直观上波动性较小的风电功率时间序列所求得的所有波动性衡量指标值更小，且预测准确率更高(均方根误差RMSE更小)。相反，波动性较大的风电功率时间序列的所有波动性衡量指标值更大，预测准确率也更低。该实验结果表明了本文所提出的波动率r能有效衡量相同时间长度和装机容量的分布式发电功率的波动性。

表1 序列a和b的不同波动性衡量指标值和预测RMES

图3给出了风电功率时间序列a和b在不同l选取下r的变化情况。从图中可知，时间序列的波动性越大，增大l后r的变化越大，反之r的变化越小，符合前述分析。因此，在选取较大的l可以更明显地区分不同分布式发电功率时间序列的波动性。此外，观察图3还可以看出，在大约l=10后，曲线逐渐变得相对平稳，因此，本例实验中选择l=10。因此，在对比任意两个分布式发电时间序列时，也可以采用画出如图3的曲线以选取合适的l。

4.2 风电功率时间序列的平滑效应

文献[24]已经验证，风电功率时间序列会随着风力机数量的逐渐汇聚(功率相加)呈现出波动性逐渐减小的趋势。这种现象称为风电功率时间序列的平滑效应。平滑效应的产生原因在于：由于每个风力机的出力的随机性较强，多台风力机的出力在汇聚(功率相加)过程中发生了部分波动的相互抵消，从而使得总出力相对于各个风力机的出力更加平滑。

为进一步验证本文所提波动率的有效性，用定义的指标检验风电功率时间序列的平滑效应是一种证明指标有效性的值得信赖的方法。

本部分实验中考察了风电场中从单台风力机到132台风力机出力下的r值(l=10，T=2880)，结果如图4所示。

从图4可以看出，随着风力机汇聚台数的增加，风力机汇聚出力的波动率r逐渐减小，说明风力机的汇聚使得出力的波动性逐渐减小，与平滑效应一致，进一步验证了波动性指标的有效性。该实验还证明了定义的波动率r能有效衡量不同装机容量的分布式发电功率的波动性。

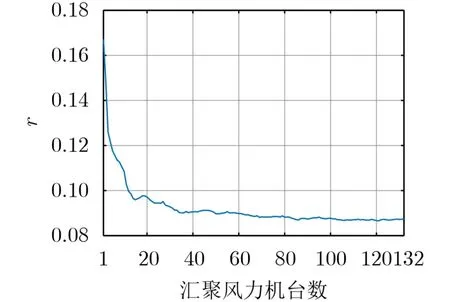
图4 风力机汇聚出力下的r

4.3 不同时间长度的风电功率时间序列的波动率r

本实验将验证波动率r在衡量不同时间长度的风电功率时间序列波动性的有效性。

除采用持续预测法和ARMA预测法、文献[13]、文献[25]和文献[26]的预测方法辅助验证外，本部分还采用了文献[17]、文献[18]和文献[19]中的波动性衡量指标进行对比验证。所验证的风电功率时间序列分别为：风电功率时间序列c：装机容量为49.5 MW，时间长度为T=720 min(半天)；风电功率时间序列d：装机容量为49.5 MW，时间长度为T=1440 min(1天)。

结果如表2所示。

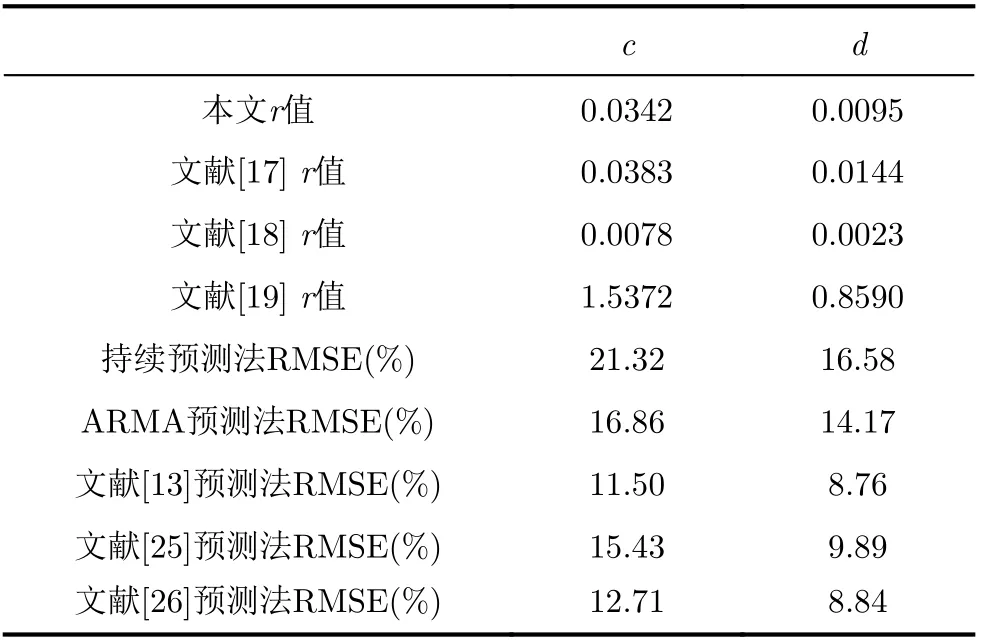
表2 不同装机容量和时间长度下风电功率时间序列的波动性对比验证

从表中可以看出，预测结果和文献[17]、文献[18]和文献[19]波动性衡量指标与波动率r比较一致地反映出风电功率时间序列c的波动性比风电功率时间序列d的波动性更大。证明了波动率r在衡量不同时间长度的风电功率时间序列波动性的有效性。

4.4 波动率r的优越性分析

为了进一步验证本文所提出的波动率r在衡量分布式发电功率波动性的有效性和优越性，本部分实验基于高频波动基本相同但变化趋势波动不同的风电功率时间序列，将波动率r与文献[17]和文献[18]定义的波动性指标进行对比分析。

风电功率时间序列e和f如图5所示，其装机容量均为49.5 MW，时间长度为5250 min，采样间隔为15 min。从图中可以看到，两个风电功率时间序列的高频波动基本相同，但时间序列e的变化趋势波动性明显小于时间序列f。

从表3的对比结果和预测结果可以看出，文献[17]和文献[18]定义的波动性指标与本文波动面积比r1均不能有效区分两个风电功率时间序列的波动性，而波动幅值比r2以及波动率r则能有效衡量出两个风电功率时间序列波动性的区别。具体原因在于，无论文献[17]和文献[18]定义的波动性指标，还是本文波动面积比r1，都是针对时间序列的高频波动而设计的，忽略了时间序列的变化趋势波动，从而导致这些指标对于如图5所示的两个风电功率时间序列产生了错误的判断。该对比实验证明了本文定义的波动率r能够更准确地刻画出分布式发电功率时间序列的波动性，体现了该指标的优越性。

表3 两个风电功率时间序列的不同波动性衡量指标对比

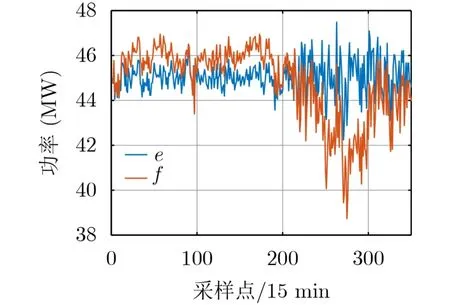
图5 高频波动基本相同但变化趋势波动不同的风电功率时间序列e和f

5 结论

本文定义了一种定量刻画分布式发电功率波动性的指标——波动率。该指标充分考虑了分布式发电功率时间序列的高频信息和低频信息中的波动性，使其能更准确地反映出分布式发电功率的波动性。利用风电场风电功率实测数据对指标进行实验验证和对比分析，结果证明了所提出的波动率能够有效地衡量不同时间长度、不同装机容量风电功率的波动性，且相比于现有的波动性衡量指标，本文所提出的波动率能更有效地反映出相对变化趋势较大的分布式发电功率的波动性。

本文分布式发电功率波动定量评估方法的提出，有助于对风、光等分布式发电功率波动性进行更准确的认识。掌握分布式发电功率波动性的大小，有利于提高分布式新能源大规模接入下的电网信息处理分析能力，促进可再生能源在电网中的渗透，进而助力我国“碳达峰”和“碳中和”目标的实现。